
| In English | Accueil/Contact | Billard | Bélier | SNH | Relativité | Botanique | Musique | Ornitho | Météo | Aide |

Voir Sommaire.
Le site héberge plusieurs sujets additionnels courts et synthétiques. Voir Sommaire.


Bardula est un pseudonyme créé par une artiste belge qui vit actuellement et travaille en France.
Bardula crée des tableaux lumineux, dont les tableaux hypnotiques "Interférences bleues" et "Blue ice" (voir Figures 1 et 2 ci-dessus).
Sources :
Light ZOOM Lumière.
Bardula.






Voici une sélection des meilleures illusions de mouvement (voir ci-dessus Figure 1 cf. [GomboDigital], Figures 2 à 5 cf. [Sélection.ca] et Figure 6 cf. [Akiyoshi Kitaoka]) :
1. Vortex en rotation (Image Vectordivider via Getty Images)
2. Spirales en rotation (Image Vectordivider via Getty Images)
3. Effet hypnotisant (Image Mark Grenier via Shutterstock)
4. Défilement (Image Guten Tag Vector via Shutterstock)
5. Grille scintillante (Image Mark via Shutterstock)
6. "Expanding pupils" (Image de Akiyoshi Kitaoka)
Sources :
Sélection du Reader's Digest (Canada) - 24 illusions d'optique complètement étourdissantes.
GomboDigital - 5 illusions d'optique qui vont vous scotcher/.
Akiyoshi Kitaoka - Anomalous motion illusions 35.




L'Auteur de ce site a réalisé quatre sculptures éoliennes installées dans son jardin à Berrac (Gers).
Description :
Conception :
Ces sculptures sont fabriquées avec des produits de récupération (rails en aluminium pour ossature d'isolation thermique, bols de camping en PVC, flancs de bidon en plastique, balle de tennis, fer à béton, etc.).
Tous les éléments mobiles sont portés sur roulement à billes.
Tous les éléments fixes sont assemblés par visserie inox.
Les sculptures sont fixées au sol par un mât vertical (piquet de clôture en acier galvanisé ou ancien tuyau d'eau en acier).



Pierre Luu est un sculpteur français qui a créé des sculptures à mouvements imprévisibles, mues par le vent ou l'eau, dont l' "éolienne à mouvements aléatoires" (voir Figures ci-dessus, et vidéo "Mobile eolien art cinétique" dans [Pierre Luu]).
Description :
Figure 1 ci-dessus : vue générale (cf. [Art et Eau]).
Figure 2 ci-dessus : zoom sur angle de vrillage des pales (séquence 0:12 de la vidéo).
Figure 3 ci-dessus : zoom sur longueur des pales (séquence 0:22 de la vidéo).
L' "éolienne à mouvements aléatoires" est composée de 5 pièces mobiles en équilibre instable (cf. [Pierre Luu - Quelque chose ne tourne pas rond][Art et Eau - Quelque chose ne tourne pas rond]).
L'équilibre est d'autant plus instable qu'il n'y a pas de girouette pour orienter la sculpture dans la direction du vent. La boule bleue est esthétique et symbolise la Terre (cf. mail du 5/3/2023 de Pierre Luu à Régis Petit).
Les deux pales sont de taille différente avec une rotation secondaire imbriquée dans la rotation principale (cf. [Pierre Luu - Eolide].
La sculpture s'anime lentement et change de forme grâce à l'action du vent. Le mouvement s'entretient par inertie du fait de l'équilibre des masses (cf. [Art et Eau - Quelque chose ne tourne pas rond]).
La sculpture se déploie dans une chorégraphie énigmatique et ne trouve une stabilité provisoire que lorsque les pales atteignent une certaine vitesse (cf. [Pierre Luu - Quelque chose ne tourne pas rond]).
Conception :
L'ensemble est conçu dans une recherche d'équilibre entre les masses, les centres de gravité, les superficies exposées au vent et les angles relatifs des surfaces (cf. [Pierre Luu - Quelque chose ne tourne pas rond]).
Les éléments mobiles sont fixés au moyen de roulements à billes pour toutes les sculptures en version projet (cf. mail du 7/3/2023 de Pierre Luu à Régis Petit). Cette association permet des rotations et déplacements fluides même par vent faible (cf. [Pierre Luu - Fragments mobile éolien).
Matériau : acier inoxydable et matériaux composites (cf. [Art et Eau - Quelque chose ne tourne pas rond]).
Hauteur : 3 m 50 (cf. [Art et Eau - Quelque chose ne tourne pas rond]).
Sources :
Pierre Luu - Mobile eolien art cinétique (YouTube, 01:57).
Pierre Luu - Un art en mouvement - Sculptures éoliennes et mobiles.
Pierre Luu - Un art en mouvement - Quelque chose ne tourne pas rond.
Pierre Luu - Un art en mouvement - Fragments mobile éolien.
Pierre Luu - Un art en mouvement - Eolide.
Pierre Luu - Un art en mouvement - Solaris : sculpture éolienne et solaire autonome en énergie.
Art et Eau - Ellipse, quelque chose ne tourne pas rond.



Jeff Kahn est un sculpteur américain qui a créé des sculptures cinétiques, intitulées "Forces invisibles", à partir d'aluminium et d'acier inoxydable.
Ces sculptures explorent l'équilibre et la gravité et comment des courants d'air presque imperceptibles interagissent avec elles. Elles sont extrêmement sensibles au milieu ambiant (faibles brises, chaleur du soleil, poids de la rosée du matin). Voir Figures 1, 2 et 3 ci-dessus montrant trois sculptures particulières : "Astrolabe", "Naked Alien" et "I Ching".
L'atelier de Jeff Kahn est situé à Lenhartsville, Pennsylvanie, USA.
Sources :
Jeff Kahn - Biographie.
Jeff Kahn - Catalogue.
Jeff Kahn - Videos.



Anthony Howe est un sculpteur américain qui a créé des sculptures mobiles hypnotiques, dont "Di-Octo" en 2014 (voir Figures 1, 2 et 3 ci-dessus, et vidéo "Di-Octo" dans [Anthony Howe] et [KULTT]).
Anthony Howe vit actuellement à Eastsound, sur l'île d'Orcas, comté de San Juan, dans l'Etat de Washington (USA).
Description :
Di-Octo est une sculpture mobile mi-pieuvre, mi-étoile, mue par le vent et quasi-silencieuse.
L'original Di-Octo, conçu et fabriqué par Anthony Howe, a été industrialisé en deux exemplaires identiques par Show Canada Inc (aciérie de Laval au Québec) comme suit (cf. mail du 10/03/2023 de David Boulay (Show Canada Inc) à Régis Petit) :
Conception :
Di-Octo a 8
mètres de haut, 3 mètres de diamètre, pèse 725 kilogrammes et ne nécessite que 2 km/h de vent pour que ses pièces mobiles s'activent (cf. [Université Concordia]).
Di-Octo est composée de 36 bras portant chacun 16 coupoles en acier très fin et tournant autour d'un anneau circulaire vertical. Les liaisons inter-bras sont de type roue intermédiaire à doigts d'entraînement. Voir détail en Figure 3 ci-dessus (cf. [Show Canada]).
Les bras tournent toujours dans le même sens, quelle que soit la direction du vent. Cela est dû à la forme des coupoles (cf. mail du 19/03/2023 de David Boulay à Régis Petit) :
Di-Octo est entièrement fabriquée en acier inoxydable 316, ce qui lui confère une meilleure résistance à la corrosion ainsi que des propriétés non-magnétiques (cf. [Show Canada]).
Autres sculptures similaires :
Anthony Howe a conçu et fabriqué d'autres sculptures similaires à Di-Octo (cf. [Anthony Howe, https://www.howeart.net/about]) :
Sources :
Anthony Howe.
Anthony Howe - Shindahiku (Fern pull).
The DC Blike Blogger - Shindahiku (Fern Pull).
KULTT - Les sculptures hypnotiques d'Anthony Howe.
Anthony Howe - Di-Octo (Youtube 1:10).
Anthony Howe - Di-Octo (long version) (Youtube 1:33).
Université Concordia - Di-Octo : captivant, cinétique et unique.
Show Canada.
JuanG3D : Di-Octo 3D Model.
What's on - Check out these alien-esque kinetic sculptures in Dubai.
UAE - Famous American artist brings kinetic sculptures to Dubai.
reddit - "Octo II", Anthony Howe, stainless steel, 2013..


Jennifer Townley est une artiste néerlandaise qui a créé des sculptures mobiles hypnotiques, dont "Asinas" en 2015 (voir Figure 1 ci-dessus, et vidéo "Asinas").
Vu à l'arrêt de face, on croirait voir une double hélice, telle l'habituelle représentation de l'ADN.
Description (cf. [Jennifer Towley]) :
"Asinas" est une sculpture mobile composée de deux hélices qui s'entrelacent et glissent l'une dans l'autre, produisant un mouvement fluide et naturel.
Les deux hélices tournent lentement dans des directions opposées et à des vitesses légèrement différentes, ce qui transforme progressivement la sculpture.
Une démonstration du fonctionnement de cette sculpture permet de mieux comprendre cette description (voir vidéo "Asinas Working Demonstration" dans [Amogh Jadhav] et vidéo "SolidWorks Mechanical Sculpture" dans [tecnoloxia.org]).
Conception :
Les soixante-cinq briques blanches en bois qui forment les deux hélices augmentent de taille vers le milieu de la sculpture, lui donnant une forme conique.
Chaque brique a la forme d'un Z dont les angles font 90°. Les briques d'une hélice sont fixées sur l'axe de rotation. Les briques de l'autre hélice sont reliées entre elles par de petites entretoises (voir Figure 2 ci-dessus issue de [Amogh Jadhav]).
Les briques sont en bois peint. Le chassis est en acier ainsi que toutes les pièces reliant les engrenages à leurs axes, les roulements au chassis, etc.
Ensuite, il y a toutes les autres pièces : un moteur électrique, des engrenages droits et des pignons en acier lourd, deux courroies et de nombreux roulements (cf. [The Plus Paper]).
Sources :
Asinas - Jennifer Townley - 2015 - Kinetic art (Youtube 2:31).
Jennifer Townley - Asinas.
L'Usine Nouvelle - Hypnotiques, ces sculptures cinétiques vous étonneront.
Amogh Jadhav - Asinas.
Amogh Jadhav - Asinas Working Demonstration (Youtube 2:14).
tecnoloxia.org - As esculturas cinéticas de Jennifer Townley.
MadCadSkills : Jennifer Townley - SolidWorks Mechanical Sculpture (Youtube 3:43).
The Plus Paper - Asinas : Fluent Movement ( http://www.thepluspaper.com/2015/03/23/asinas-fluent-movement/ ).
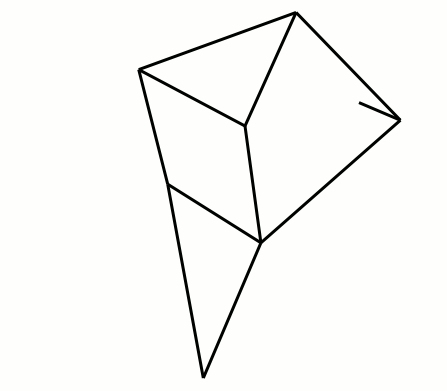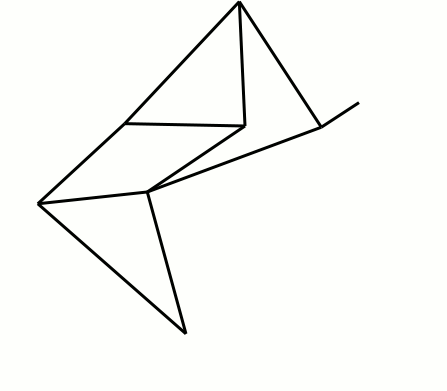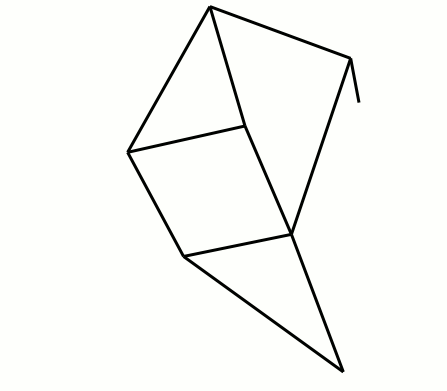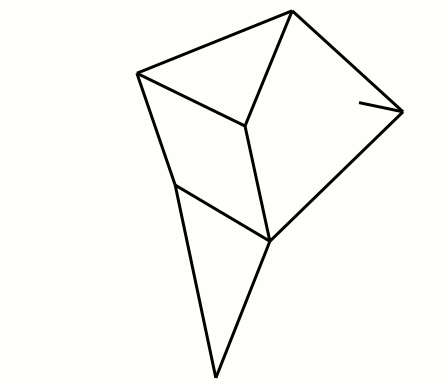
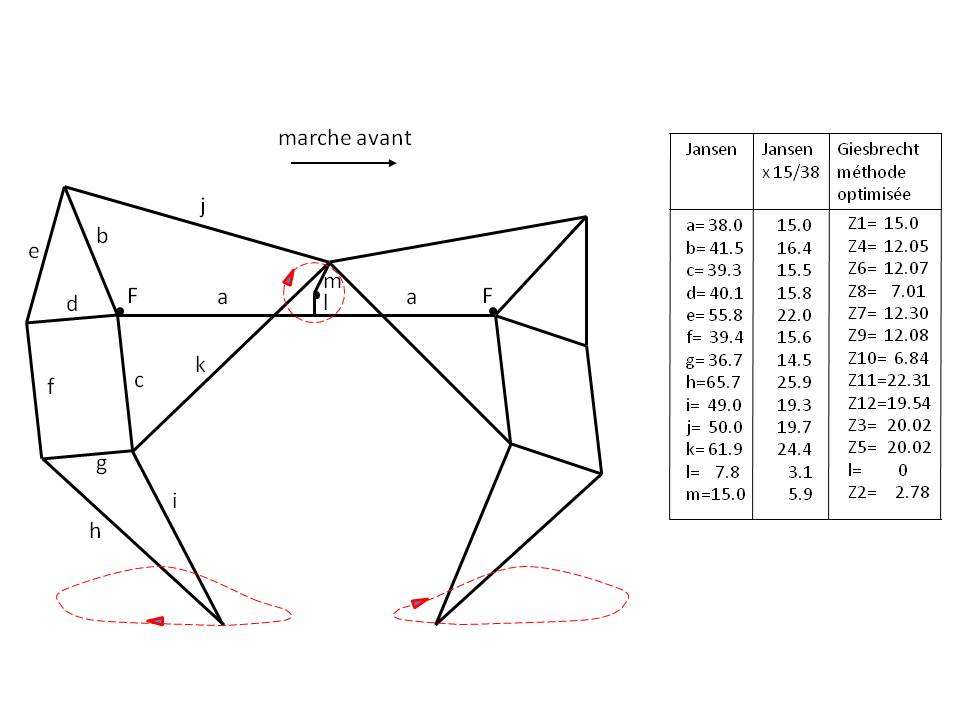
Theo Jansen est un sculpteur néerlandais qui a créé en 1991 des créatures étranges, dont le robot marcheur (voir Figures 1 et 2 ci-dessus).
Fonctionnement :
Ce robot marcheur est un mécanisme à pattes très légères qui peut se déplacer sur un plan horizontal sous l'action du vent, ou sur un plan incliné sous l'action de son propre poids (voir vidéo, cf. [Jansen, Plaudens Vela]).
Le seul actionneur du robot est un vilebrequin central faisant la liaison entre les pattes et le corps du robot (voir roue de couleur rouge en Figure 2, et aussi [Exergia]).
Pour un robot à trois paires de pattes, le vilebrequin possède trois manivelles décalées successivement de 120° pour avoir un mouvement constant du robot pendant la phase propulsive (voir Figure 2).
Description du corps :
Le corps du robot se compose d'une plate-forme horizontale (longueur 2a) et de supports fixes verticaux (longueur l) portant le vilebrequin (excentricité m). Voir Figure 3 ci-dessus.
La double longueur (a) de la plate-forme est calculée pour assurer la non-collision entre pattes avant et pattes arrière.
La longueur (l) des supports est modifiable pour assurer un mouvement d'ensemble horizontal du robot. Augmenter ou diminuer la longueur (l) revient à faire pivoter l'ensemble des barres de chaque patte autour de chaque point fixe F.
Description des pattes :
Chaque patte est constituée de dix barres articulées (barres b à k) dont deux forment un lien rigide (barres e et h)). Voir Figure 3 ci-dessus.
Les deux pattes d'une même paire sont identiques et en miroir l'une de l'autre de chaque côté du vilebrequin.
Le pied de chaque patte décrit une courbe ovoïde dont la partie inférieure est quasiment plate et horizontale, permettant ainsi au pied d'être au contact avec le sol pendant la phase propulsive.
En phase retour, le pied décolle du sol et le robot peut enjamber de petits obstacles sans trop soulever son corps.
Le tableau de la Figure 3 donne la longueur de chaque barre selon différents auteurs :
Sources :
Jansen - Plaudens Vela.
Jansen - plaudens vela 1 (Youtube 0:53).
Wikipedia - Mécanisme de Jansen.
Exergia - Simulation von Theo Jansen's Strandbeest.
Giesbrecht Daniel - Design and optimisation of a one-degree-offreedom eight-bar leg mechanism for a walking machine.
Les fichiers suivants décrivent le patrimoine monumental et architectural de 140 communes situées à moins de 20 km des villes de Lectoure ou de Condom dans le Gers (France), et comprenant la Lomagne gersoise et ses environs.
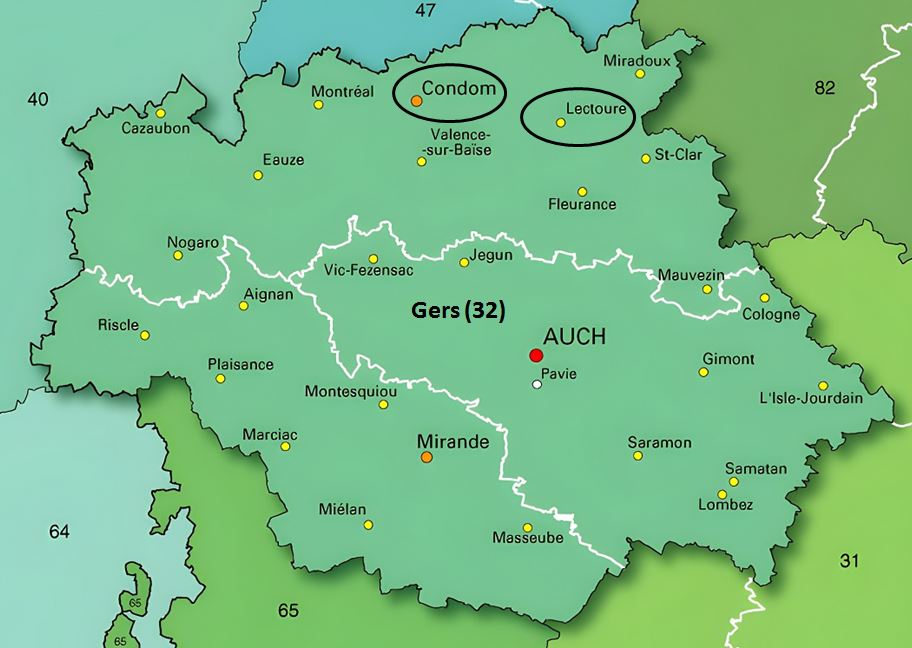
Liste des communes :
Les communes sont listées alphabétiquement, chacune étant suivie du numéro de département : Gers (32 par défaut), Lot-et-Garonne (47), Tarn-et-Garonne (82).
Chaque fichier pdf pèse environ 500 Ko, le plus lourd étant Lectoure (3.3 Mo).
Sources :
- Wikipedia, Descriptif de chaque commune dont département, toponymie, histoire, maire, nombre d'habitants, altitude, lieux et monuments.
- Ministère de la Culture, Immeubles protégés au titre des Monuments Historiques, par département et par commune. N'inclut pas les sites protégés.
- Ministères Ecologie Energie Territoires, Liste des servitudes des sites et monuments du Gers jusque janvier 2015, par commune et incluant la protection des sites et des monuments au titre des Monuments Historiques.
- SDAP renommé STAP (Services Territoriaux de l'Architecture et du Patrimoine), Liste des monuments historiques et des sites du Lot-et-Garonne, par commune et jusqu'en 2006.
- DREAL Midi-Pyrénées (Direction Régionale de l'Environnement, de l'Aménagement et du Logement Midi-Pyrénées), Bilan des sites classés et inscrits du Tarn-et-Garonne, avril 2013, par commune.
- Ministère de la Culture, Base Mérimée du patrimoine monumental français, par commune et par monument incluant date d'origine, lieu, descriptif et propriété.
- Comet Anaïs Villages et bourgs de la Gascogne gersoise à la fin du Moyen Age (1250-1550), par commune, Thèse d'histoire, 2017, Volume 1 : Synthèse (405 p), Volume 2 : Figures (442 p), Volume 3 : Notices (680 p), Volume 4 : Atlas (391 p).
- Google, Recherche par commune (histoire, origine du nom, bastide, castelnau, castrum, fortification, rempart, château, fossé, vestige) ou par monument (protection récente des monuments et des sites au titre des Monuments Historiques)
- Google Images et Google Vidéos, Recherche par commune (monument, "carte postale", vidéo Youtube).
- IGN (Institut Géographique National, renommé Institut National de l'information Géographique et forestière), Géoportail, par commune (situation graphique des lieux-dits et des rues).
- Google, Google Maps, par commune (situation GPS des lieux-dits, rues principales, photos par Street View).
- Google, Recherche par commune (cadrans solaires, moulins, pigeonniers, puits, fontaines, lavoirs).
- Mapio, Photos d'internautes avec titre et géolocalisation précise. Recherche par Région, Département, Arrondissement, Commune.
Voir détail.

B4.1. Introduction :
La mnémotechnique regroupe l'ensemble des techniques destinées à faciliter la mémorisation et le rappel d'informations grâce à des associations mentales.
Parmi ces procédés, la méthode des articulations chiffrées [WIK] se distingue par son efficacité pour retenir des nombres. Ce système repose sur une correspondance fixe entre les chiffres de 0 à 9 et des sons de type consonne. Par exemple, 3 correspond au son "m". En ajoutant librement des voyelles, on transforme les suites de chiffres en mots concrets, plus faciles à mémoriser. Par exemple, le nombre 42 peut devenir le mot mouton (m = 3, t = 1).
La table de rappel des chiffres (de 0 à 9) fut mise au point au 19e siècle par Aimé Paris [PAR, p.28], puis reprise à l'identique par l'abbé François-Napoléon-Marie Moigno [WIK]. Une version différente et plus simple fut ensuite proposée par Joe Bertin [BER] en 2018, reprise quasiment à l'identique par Régis Petit en 2025.
La table de rappel des nombres de 00 à 99 attribue, quant à elle, un mot concret à chacun de ces nombres.
Les étapes de la méthode des articulations chiffrées sont les suivantes :
1. Associer chaque chiffre de 0 à 9 à un son de type consonne, selon un code à retenir par coeur (voir Table de rappel des chiffres).
2. Convertir la suite de chiffres à retenir en une suite de sons, conformément à ce code.
3. Former une suite de mots à partir de ces sons en ajoutant des voyelles, de manière à créer phonétiquement une phrase, ou mentalement une histoire imagée et marquante.
4. Pour restituer les chiffres, procéder à l'inverse : histoire, mots, sons, chiffres.
Exemple d'histoire en français que l'on peut construire soi-même pour retenir les premières décimales du nombre Pi = 3, 14 15 92 65 35 89 79 32 38... :
- Selon table de rappel des chiffres de Aimé Paris : "assis par TeRre sur une modeste ToiLe, je suis en PaNne et GèLe. Au loin, près d'une MeuLe de foin, se trouve une VamP portant une CaPe de MoiNe et des MouFles."
- Selon table de rappel des chiffres de Régis Petit : "sur mon TanK, à côté d'une TaSse, d'une PoiRe et d'une GouSse d'ail, j'écoute la MeSse, quand surgit un BiP sonore. J'éclaire avec ma LamPe et vois une MaRe avec un MeuBle en plein milieu."
Applications :
Parmi les applications où la méthode des articulations chiffrées apporte un réel bénéfice, on peut citer :
- les numéros de téléphone codés en 5 mots concrets de deux chiffres chacun (exemple : 06 12 34 56 78)
- les dates anniversaire codées en 4 mots concrets (exemple : 24 02 1958)
- les codes d'accès (code PIN, code de porte d'immeuble, de coffre-fort, d'alarme, etc.) codés en 2 ou 3 mots concrets selon leur longueur
- les numéros de sécurité sociale codés en un chiffre initial (genre : 1 homme, 2 femme) suivi de 7 mots concrets (exemple : 1 58 02 XX XX XX XX XX)
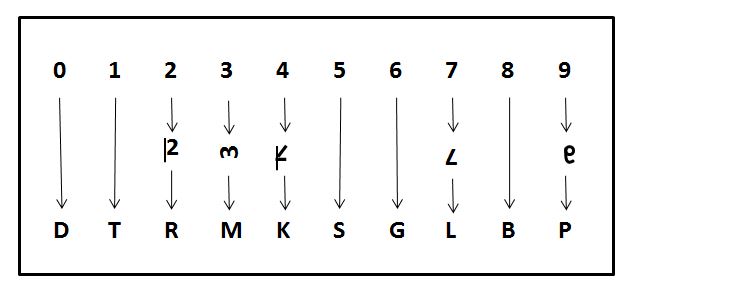
B4.2. Tables de rappel des chiffres de 0 à 9 :
La table de rappel des chiffres de 0 à 9 n'est pas unique et dépend de son auteur :
- Celle de Aimé Paris a le mérite de codifier tous les sons courants de type consonne. L'association entre chiffre et son(s) doit être mémorisée par coeur.
- Celle de Joe Bertin associe une lettre de type consonne à chaque chiffre, ce qui fournit un support visuel facilitant grandement la mémorisation des sons.
- Celle de Régis Petit reprend la table de Joe Bertin en y modifiant les lettres associées aux chiffres 2 et 4, ce qui améliore le support visuel (voir Figure ci-dessus).
Les différentes tables sont les suivantes :
Légende du tableau : (*) selon l'écriture orthographique des phonèmes.
| Chiffre | Son (*) et image selon Aimé Paris [PAR, p.28][WIK][APP] | Autre image selon Régis Petit | Son (*) et image selon Joe Bertin [BER] | Son (*) et image selon Régis Petit |
|---|---|---|---|---|
| 0 | "s" ou "z", une des boucles du s | SanS aide | "d", lettre D | "d", lettre D |
| 1 | "t" ou "d", jambage unique de la lettre t | TenDu ou Tout Droit | "t", lettre T | "t", lettre T |
| 2 | "n" ou "gn", double jambage de la lettre n | Na ! (attitude enfantine de provocation) | "n", lettre N de côté | "r", lettre R sans barre verticale |
| 3 | "m", triple jambage de la lettre m | Maman | "m", lettre M de côté | "m", lettre M de côté |
| 4 | "r", lettre r à l'envers ou en miroir | trois Ratures faites avec Rage | "r", lettre R en miroir | "k", lettre K (avec bloc de trois traits) |
| 5 | "l", similaire à la lettre L en écriture ronde cursive française [LIV1][LIV2] | Ligne verticale ratatinée | "s", lettre S | "s", lettre S |
| 6 | "ch" ou "j", similaire à la lettre j en écriture ronde cursive française [LIV1][LIV2] | Chat qui Jaillit | "g" ou "j", lettre G | "g" ou "j", lettre G |
| 7 | "k" ou "g", forme de potence semblable à la lettre q ou g | Coups Guerriers (indiqués par deux Coupures) | "l", lettre L à l'envers | "l", lettre L à l'envers |
| 8 | "f" ou "v", similaire à la lettre F en écriture ronde cursive française [LIV1][LIV2] | FèVe (sous forme de petit enFant) | "b", lettre B | "b", lettre B |
| 9 | "p" ou "b", lettre p en miroir ou lettre b à l'envers | Petit Bébé (en position foetale avec sa grosse tête) | "p", lettre P en miroir | "p", lettre P en miroir |
B4.3. Tables de rappel des nombres de 00 à 99 :
Chacun peut construire librement sa table de rappel des nombres de 00 à 99, conformément à une table de rappel des chiffres donnée.
Les tables de rappel des nombres de 00 à 99 proposées ci-dessous ont été créées par Régis Petit. La première est conforme au codage des chiffres par Aimé Paris, la seconde au codage des chiffres par Régis Petit.
Ces deux tables sont conçues selon les règles suivantes, permettant une mémorisation facile des mots concrets :
Mot concret = nom commun ou propre, à une seule syllabe de type CVC ou CSVC, tel que :
C = consonne associée au chiffre dans la table de rappel des chiffres.
V = voyelle pouvant être (*) : "é" "è" "eu" "in" "a" "an" "ou" "o" "on" "i" "u"
S = semi-consonne en attaque d'une voyelle V, pouvant être (*) : "w" "y" "u+"
le noyau V ou SV de la syllabe étant choisi prioritairement parmi les sons (*) : "é" "è", "eu", "in" ; "a", "an" ; "ou", "w" V ; "o", "on" ; "i", "y" V ; "u", "u+" V
(*) selon l'écriture orthographique des phonèmes.
Les exceptions à ces règles sont mises en italique dans ces tables.
| Nombre | Mot concret conforme au codage des chiffres par Aimé Paris | Mot concret conforme au codage des chiffres par Régis Petit |
|---|---|---|
| 00 | Sas | Dinde |
| 01 | Soute | Datte |
| 02 | Scène | Dard ou Dur |
| 03 | Somme | Dame |
| 04 | Serre ou Soeur | Dock ou Duc |
| 05 | Selle | Danse |
| 06 | Souche | Danger ou Dingue |
| 07 | Sac | Dalle |
| 08 | Soif | Dab ou Daube |
| 09 | Sep | Dieppe ou Dupe |
| 10 | Tasse | Tiède |
| 11 | Tête ou Tente | Tête ou Tente |
| 12 | Tonne | Terre |
| 13 | Tome | Tome |
| 14 | Terre | Tank |
| 15 | Toile | Tasse |
| 16 | Tache | Tige ou Tag |
| 17 | Tank | Toile |
| 18 | Touffe | Tombe |
| 19 | Taupe | Taupe |
| 20 | Nasse | Rade |
| 21 | Natte | Rate |
| 22 | Nonne | Rire |
| 23 | Nem | Rame |
| 24 | Nerf | Rack |
| 25 | Nul | Race |
| 26 | Niche | Rage ou Reg |
| 27 | Nuque | Râle |
| 28 | Nef | Rab ou Robot |
| 29 | Nappe | Rampe ou Repas |
| 30 | Messe | Mode |
| 31 | Meute ou Motte | Meute ou Motte |
| 32 | Moine | Mer ou Mare |
| 33 | Môme | Môme |
| 34 | Mer ou Mare | Mec |
| 35 | Meule ou Malle | Messe |
| 36 | Mèche | Mage ou Mangue |
| 37 | Mec | Meule ou Malle |
| 38 | Moufle | Meuble |
| 39 | Myope | Myope |
| 40 | Race | Coude |
| 41 | Rate | Quinte ou Côte |
| 42 | Reine | Coeur |
| 43 | Rame | Came |
| 44 | Rire | Cake |
| 45 | Râle | Caisse |
| 46 | Roche | Cage |
| 47 | Rack | Cale |
| 48 | Rouf ou Rêve | Cube |
| 49 | Râpe | Coupe ou Cape |
| 50 | Laisse | Soude |
| 51 | Latte | Soute |
| 52 | Laine | Serre ou Soeur |
| 53 | Lame | Somme |
| 54 | Lard | Sac |
| 55 | Lille | Sas |
| 56 | Louche | Singe ou Sangle |
| 57 | Lac | Sel |
| 58 | Lymphe | Sabre |
| 59 | Loupe | Soupe |
| 60 | Chasse | Jade ou Guide |
| 61 | Jante ou Chatte | Jatte ou Goutte |
| 62 | Jeune ou Chaîne | Jour ou Gare |
| 63 | Gym ou Chaume | Gym ou Gamme |
| 64 | Jour ou Chair | Jonque |
| 65 | Gel ou Châle | Gousse |
| 66 | Juge | Juge ou Gong |
| 67 | Jonque ou Chèque | Gel ou Gueule |
| 68 | Chef | Jambe |
| 69 | Jupe ou Chappe | Jupe ou Guêpe |
| 70 | Caisse | Lad ou Lande |
| 71 | Quinte ou Côte | Latte |
| 72 | Canne | Lard |
| 73 | Came | Lame |
| 74 | Coeur | Lac |
| 75 | Cale | Laisse |
| 76 | Couche | Linge ou Langue |
| 77 | Cake | Lille |
| 78 | Coiffe | Lobe |
| 79 | Coupe ou Cape | Lampe |
| 80 | Fesse | Bande |
| 81 | Fête | Bête |
| 82 | Fouine | Beurre |
| 83 | Femme | Boum |
| 84 | Fer | Banque |
| 85 | Foule ou Fil | Bosse |
| 86 | Fiche ou Vache | Bouge ou Bague |
| 87 | Fac | Balle |
| 88 | Fief | Bob |
| 89 | Vamp | Bip |
| 90 | Pince | Panda ou Poudre |
| 91 | Patte | Patte |
| 92 | Panne | Poire |
| 93 | Pomme | Pomme |
| 94 | Père | Pack ou Pique |
| 95 | Pelle | Panse |
| 96 | Pêche | Page |
| 97 | Pack ou Pique | Pelle |
| 98 | Pouf | Pub ou Poubelle |
| 99 | Pape ou Poubelle | Pape |
B4.4. Sources :
[APP] Apprendre5minutes, Comment mémoriser facilement les chiffres ou les nombres
[BER] Joe Bertin, Astuce de mémorisation : la table de rappel
[LIV1] French Handwriting Schoolbook, écriture ronde française
[LIV2] pilllpat (agence eureka), album Alphabete
[PAR] Aimé Paris, Exposition et pratique des procédés mnémotechniques à l'usage des personnes qui veulent étudier la mnémotechnie en général comme un moyen d'abréger l'étude de toutes les connaissances humaines, Paris, 1825
[WIK] Wikipedia, Code chiffres-sons
B5.1. Introduction :
Un palindrome est une forme de symétrie linguistique où une phrase (pouvant se limiter à un seul mot) se lit ou s'entend de la même manière dans les deux sens.
Les palindromes orthographiques reposent sur l'ordre des lettres dans l'écriture, comme dans C'est sec. Voir Phrases palindromes attribuées, Phrases palindromes anonymes, Villes palindromes et Prénoms palindromes.
De même pour les palindromes de mots qui reposent sur l'ordre des mots dans l'écriture, comme dans "Un pour tous, tous pour un".
De même pour les palindromes syllabique au niveau de la prononciation par syllabes, comme dans "Laconique Nicolas" correspondant à la suite syllabique "la" "ko" "ni" "ke" "ni" "ko" "la".
De même pour les palindromes phonétiques au niveau de la prononciation par phonèmes, comme dans "Il aima Amélie" correspondant à la suite phonétique "i" "l" "é" "m" "a" "a" "m" "é" "l" "i".
De même pour les palindromes numériques au niveau de l'écriture, comme dans la date "02/02/2020".
De même pour les palindromes rotationnels qui se lisent de manière identique après pivotement de l'ensemble d'un demi-tour, comme dans le mot "inoui".
De même pour les palindromes miroirs qui se lisent de manière identique après réflexion dans un miroir.
De même pour les palindromes musicaux au niveau des notes de la phrase musicale.
Les palindromes listés ci-dessous sont exclusivement des palindromes orthographiques de langue française, où l'on ne tient pas compte de la casse (majuscules/minuscules), des signes diacritiques (accent, tréma, cédille, tilde, etc.), des espaces et des signes de ponctuation (point, virgule, tiret, parenthèse, etc.).
B5.2. Phrases palindromes attribuées :
Les plus belles phrases palindromes de langue française, attribuées à un auteur, sont les suivantes :
A Cuba, Anna a bu ça (Gérard Durand).
A Laval, elle l'avala (Michel Laclos).
A l'étape, épate-la ! (Louise de Vilmorin).
A révéler mon nom, mon nom relèvera (Edmond Rostand, dans Cyrano de Bergerac).
Ce satrape repart à sec (Pierre Bailly).
C'est sec (Roger Cornaille).
Eh ! ça va la vache ? (Louise de Vilmorin).
Elisa, là, à l'asile (Lennig Gullon).
Elu par cette crapule (Charles Cros).
Emile-Eric, notre valet, alla te laver ton ciré élimé (Georges Perec).
Engage le jeu que je le gagne (Alain Damasio).
En nos repères, n'insère personne (Dominic Bergeron).
En route je tourne (Roger Cornaille).
Eric, notre valet, alla te laver ton ciré (Jacques Capelovici).
Esope reste ici et se repose (Jacques Capelovici).
Etel, un port trop nu, l'été (Claude Gaignière).
Et la Marine va venir à Malte (attribué à Victor Hugo).
Et Luc colporte trop l'occulte (Michel Laclos).
Et Tesio, né borné et naïf, emporte une vedette devenue trop méfiante en robe noisette (Francis Pacherie).
Karine égarée rage en Irak (Gérard Durand).
Karine libre à Erbil en Irak (Christophe L.)
La Marine en ira mal (attribué à Victor Hugo).
La mariée ira mal (Louise de Vilmorin).
L'âme des uns n'use de mal (Etienne Pasquier).
L'amer vin enivre mal (Jean T.).
La mère Gide digère mal (Louis Scutenaire).
L'âme sûre ruse mal (Louise de Vilmorin).
L'ami naturel ? Le rut animal ! (Louise de Vilmorin).
Lune de ma dame d'été, été de ma dame de nul (Louise de Vilmorin).
Nier est effet serein (Stéphane Susana).
Noël a trop par rapport à Léon (Sylvain Viart).
Oh ! cet écho (André Tomkins).
Par-delà le drap (Patrick Hospital).
Rions noir (Jacques Bens).
Rue Verlaine gela le génial rêveur (Jacques Perry-Salkow).
Ta bête te bat (Louise de Vilmorin).
Un art luxueux ultra nu ! (Matthieu Godbout).
Un émir fada, venu du Nevada, frime nu (Gérard Durand).
B5.3. Phrases palindromes anonymes :
Les plus belles phrases palindromes de langue française, sans auteur connu, sont les suivantes :
A l'autel elle alla, elle le tua là.
Bon sport, trop snob.
Car, tel Ali, il a le trac.
Ce mec.
essayasse.
Etna : lave dévalante.
Etre là, alerte.
Et se resservir, ivresse reste.
Ici.
Il a pâli.
Il a sali.
Karine alla en Irak.
L'âge légal.
La malade pédala mal.
L'âme d'Eve rêve de mal.
La mère puce récupère mal.
L'âne vénal.
malayalam (langue parlée en Inde).
mon nom.
Nie, reste net, serein.
Ni lac, ni patelin, ni le tapin câlin.
Oh ! Cela te perd, répéta l'écho.
ressasser.
Réussir à Paris : suer.
rotavator.
S'engager à revers : rêver à regagnes !
Sexe vêtu, tu te vexes ?
Ta belle porte s'use trop, elle bat.
Trace là mon nom à l'écart.
Un drôle de lord nu.
Un ému a son os au menu.
Un enfer bref. Né nu.
Un été nu.
Un rêve de ver nu.
Un roc lamina l'animal cornu.
Un roc si biscornu.
Zeus a été à Suez.
B5.4. Villes palindromes :
Les principales villes palindromes du monde sont les suivantes :
Allemagne : Burggrub (Bavière), Hammah (Basse-Saxe), Mussum (Rhénanie-du-Nord-Westphalie), Woddow (Brandenburg), Zeez (Mecklenburg-Vorpommern)
Angola : Seles (Cuanza Sul)
Arabie Séoudite : Al'Ula (Madinah)
Argentine : Neuquén (Patagonie)
Australie : Aramara (Queensland), Arrawarra (Nouvelle-Galles-du-Sud), Civic (Territoire de la Capitale Australienne), Glenelg (Adélaïde, Australie-Méridionale), Hattah (Victoria), Lal Lal (Victoria), Parap (Territoire du Nord), Paraparap (Victoria), Tumut (Nouvelle-Galles-du-Sud)
Belgique : Eke, Ellemelle (Province de Liège), Ere
Brésil : Aba (Bahia), Acaiaca (Minas Gerais), Aia (Ceara), Mutum (Minas Gerais)
Burkina Faso : Bob (Région du Centre-Ouest)
Canada : Elôle (Québec), Kinikinik (Alberta), Laval (Québec), Navan (Ontario), Salas (Nouvelle-Ecosse), Wakaw (Saskatchewan)
Chili : Lolol (O'Higgins)
Chine : Nan'an (Fujian)
Danemark : Dragsgard, Vellev
Egypte : Aga (gouvernement de Daqahliyya)
Espagne : Aba (Pays basque), Aja, Aya, Oco, Ollo (Navarre), Oro, Oso (Catalogne), Salas (Asturie), Saras, Senés (Andalousie), Sotos
Etats-Unis : Ada (Oklahoma, Oho, Minnesota), Ala (Alabama), Anna (Ohio, Texas, Illinois), Ava (Missouri, Illinois, New York), Capac (Michigan), Civic (Canberra), Eleele (Hawaï), Hannah (Michigan, Dakota du Sud, Caroline du Nord), Harrak (Oklahoma, Washington), Ixixi (Alaska), Kanakanak (Alaska), Kinikinik (Colorado), Level (Ohio, Maryland), Noxon (Montana), Otto (plusieurs Etats), Oto (Iowa), Remer (Minnesota), Renner (Texas), Wassamassaw (nom d'une région de Caroline du Sud)
Ethiopie : Asasa, Asosa
Finlande : Asa (Laponie), Esse, Ii (Ostrobotnie), Orö
France : Afa, Callac, Esse, Eve, Eze, Laval, Noron, Noyon, Oô, Sajas, Sanas, Saras, Savas, Sées, Selles, Senones, Serres, Sos, Sus
Grèce : Sedes, Serres
Groenland : Qaanaaq (Région Qaasuitsup)
Hongrie : Tat, Tét, Pap, Ziliz
Inde : Ara (Bihar), Aramara, Atta (Uttar Pradesh), Aya (Maharashtra), Gadag (Karnataka), Idappadi (Tamil Nadu), Itamati (Odisha), Rapar (Gujarat), Nawagawan
Iran : Barab, Basab, Kahak, Karak, Kuruk, Naran, Qoroq, Sarras, Selles, Sis, Sus, Tabbat
Irlande : Navan (Comté de Meath)
Israël : Akka, Na'an
Italie : Ala (Trentin-Haut-Adige), Ateleta (Abruzzo), Erre (Podesteria, ancien nom), Onano (Latium), Onno (Lombardie), Sennes (Tyrol du Sud), Siris (Calabre)
Japon : Aka (Fukuoka), Akasaka (Tokyo, Okayama), Ama (Shimane), Awa (Tokushima), Ono (Préfecture de Hyogo)
Mali : Tamahamat, Tassassat
Maroc : Akka, Assa
Mauritanie : Tétêt (Région de l'Adrar)
Niger : Tabadabat, Tassessat
Nigeria : Aba (Etat d'Abia), Abiriba, Apapa, Elele (Rivers), Irri, Ososo, Oyo (Etat d'Oyo)
Nouvelle-Zélande : Aka Aka (Auckland)
Pays-Bas : Ede (Province de Gueldre), Ee (Province de Groningue), Epe (Province de Gueldre)
Pologne : Wolow (Basse-Silésie)
République tchèque : Vokov
Roumanie : Anina (Judet de Caras-Severin)
Royaume-Uni : Anna (Suffolk), Eve (Ecosse), Eye (Cambridgeshire, Suffolk), Glenelg (Ecosse), Notton (West Yorkshire, Angleterre)
Russie : Aga (République de Sakha) Tommot (Iakoutie), Ulu (Iakoutie), Yessey (Krasnoïarsk)
Sénégal : Matam (Région de Matam)
Suède : Abba (Province de Dalécarlie), Dörröd, Kivik, Murum
Suisse : Planalp (Obwald)
Thaïlande : Nan (Province de Nan)
B5.5. Prénoms palindromes :
Les principaux prénoms palindromes sont les suivants :
Légende : (*) indique les prénoms palindromes les plus courants en France (nées en France ou recensées dans la base "Prénoms" de l'Insee depuis 1900).
Prénoms féminins :
Ada (*), Adda
Aa
Anevena
Anina
Anona
Arezera
Afifa
Aviva
Aia, Aya
Arora
Atta
Ece
Elle (*)
Eve (*)
Hawah, Hawwah
Immi
Ireri
Ivi
Izzi
Layal
Lenel
Malayalam
Maram
Okko
Viv
Prénoms masculins :
Aba, Abba
Alla
Aoloa
Bob (*)
Did
Efe
Lehel
Nan
Natan (*), Nattan
Nayan
Neven
Odo
Oto, Otto (*)
Reber
Reinier
Sabas
Savas
Talat, Tanat
Prénoms mixtes :
Aja (*)
Ama (*), Amma
Ana (*), Anna (*), Anena, Hannah (*)
Ara
Asa
Ava (*), Awa
Axa
Aza, Azza, Aziza
Civic
Ebbe
Ede
Eme, Emme (*)
Görög
Kajak, Kayak
Lil (*), Lyl
Noon
Nosson
Ono
Siris
Uru
Yay
Zaz
B5.6. Palindromes de mots :
Les palindromes de mots sont des phrases qui se lisent à l'identique de droite à gauche et de gauche à droite au niveau des mots, indépendamment de la casse (majuscules/minuscules) et des signes de ponctuation (point, virgule, tiret, parenthèse, etc.), comme dans les exemples suivants :
Un pour tous, tous pour un
Papa aime maman, maman aime papa
Nous avions les avions, nous !
Pierre baise à Baise-Pierre
Certains palindromes de mots, moins stricts, acceptent l'omission des signes diacritiques (accent, tréma, cédille, tilde, etc.), comme dans les exemples suivants :
La juste est juste là
La foule, foule-là !
Saint-Pierre a marié Marie à Pierre Saint
B5.7. Palindromes numériques :
Les plus beaux palindromes numériques sont les suivants [PAL][VIL] :
02-02-2020
21-12-2112
121 = 38 + 83 = 121
12 345 678 987 654 321 qui est le carré du nombre palindromique 111 111 111
982 623 644 294 744 275 088 611 239 676 071 787 170 676 932 116 880 572 447 492 446 326 289 qui est le carré du nombre non palindromique 31 346 828 297 209 660 045 268 842 120 992 233 (5 juillet 2024 - Patrick De Geest)
1 030 607 060 301 qui est le cube du nombre palindromique 10 101
1 331 000 039 930 000 399 300 001 331 qui est le cube du nombre palindromique 1 100 000 011
10 662 526 601 qui est le cube du nombre non palindromique 2 201
B5.8. Palindromes rotationnels :
Les palindromes rotationnels (appelés aussi "ambigrammes rotationnels") sont des mots ou des phrases qui se lisent de manière identique après pivotement de l'ensemble d'un demi-tour.
Cette propriété concerne exclusivement les caractères suivants [AMB][DEL] :
Chiffres : 0, 1, 8 qui restent invariants par rotation, et 6/9 qui est une paire de rotation l'un de l'autre.
Signes de ponctuation : - : () [] {} qui restent invariants par rotation.
Symboles : + - / x = ≠ ∞ \ ∫ ⊗ # $ % § | θ ι ο χ qui restent invariants par rotation.
Lettres majuscules : H, I, N, O, S, X, Z qui restent invariantes par rotation, et M/W qui est une paire de rotation l'une de l'autre.
Lettres minuscules : i, l, o, s, x, z qui restent invariantes par rotation, et a/e, b/q, d/p, h/y, m/w, n/u qui sont des paires de rotation l'une de l'autre.
Les plus beaux palindromes rotationnels sont les suivants :
NON
SOS
SONOS
NOW NO SWIMS ON MON (qui signifie "Maintenant plus de piscine le lundi")
NeW MaN
aie
axe
aune
yeah
apode
inoui
sales
saxes
suons
nounou
salles
saisies
saillies
elle alla
andin basnoda a une épouse qui pue (Georges Perec).
A noter que certains mots peuvent donner un autre mot par rotation d'un demi-tour. Exemples :
91 = 90 + 01 / 10 + 06 = 19
NOM/WON
NOS/SON
las/sel
epis/sida
eues/sana
iles/sali
oued/pano
sans/sues
ailes/salie
aillé/allié
esses/sassa
assassins/suissesse
le pou / nodal
A noter également que certains mots peuvent donner le même mot ou un autre mot par rotation d'un quart de tour. Exemples :
Sens anti-horaire (où les majuscules C E H I M N O X Z deviennent respectivement U W I H E Z O X N) :
OHIO/OHIO
MON/ZOE
ZOE/WON
con/cou
Sens horaire (où les majuscules E H I N O U W X Z deviennent respectivement M I H Z O C E X N) :
OIE/OHM
ZOE/NOM
B5.9. Palindromes miroirs :
Les palindromes miroirs sont des mots ou des phrases qui présentent une symétrie axiale, horizontale ou verticale, et se lisent de manière identique après réflexion dans un miroir tenu horizontalement ou verticalement.
La symétrie horizontale inverse le haut et le bas, tout en conservant la gauche et la droite ainsi que l'ordre des lettres. BEC dans un miroir horizontal reste BEC
La symétrie verticale inverse la gauche et la droite ainsi que l'ordre des lettres au sein du mot, tout en conservant le haut et le bas. TOUT dans un miroir vertical devient TUOT
Ces propriétés de symétrie concernent exclusivement les caractères suivants [AMB][DEL] :
Symétrie horizontale :
Chiffres : 0, 1, 3, 8
Signes de ponctuation : . - : () [] {}
Symboles : + - x = > < ∑ ∞ ∫ ⊗ | € ε θ ι κ ο χ
Lettres majuscules : B, C, D, E, H, I, K, O, X
Lettres minuscules : c, i, k, l, o, x
Symétrie verticale :
Chiffres : 0, 1, 8
Signes de ponctuation : . - : " '
Symboles : + - ± x = * ∏ ∞ ⊗ ° _ | γ θ ι ν ο π τ υ χ ψ ω
Lettres majuscules : A, H, I, M, O, T, U, V, W, X, Y
Lettres minuscules : i, l, m, o, u, v, w, x
Exemples de palindromes miroirs à symétrie horizontale :
BEC
BICHE
DIODE
EXCEDEE
kilo
Exemples de palindromes miroirs à symétrie verticale :
TOT
AVIVA (3ème personne du singulier du passé simple du subjonctif du verbe aviver
MAOAM (marque de bonbons pâte à mâcher d'origine allemande)
MATAM (ville du Sénégal)
TAMAT (3ème personne du singulier de l'imparfait du subjonctif du verbe tamer)
TATAT (3ème personne du singulier de l'imparfait du subjonctif du verbe tâter)
TAXAT (3ème personne du singulier de l'imparfait du subjonctif du verbe taxer)
HAITI, AH !
MOT A TOM
wow (interjection d'origine anglaise exprimant la surprise ou l'émerveillement)
B5.10. Palindromes musicaux :

Les palindromes musicaux sont des séquences sonores construites de manière à rester identique lorsqu'elles sont lues dans un sens ou dans l'autre, selon deux types possibles de symétrie :
- La rétrogradation (B), qui consiste à rejouer la succession des notes (A) en ordre inverse dans le temps. Exemple (voir Figure ci-dessus) : la séquence originale Do Ré Mi Fa Sol La Si La Sol Fa engendre la séquence inverse Fa Sol La Si La Sol Fa Mi Ré Do.
- Le renversement (C), qui consiste à rejouer la succession des notes en inversant la direction des intervalles entre ces notes autour d'un axe horizontal imaginaire. Exemple (voir Figure ci-dessus avec Do choisi comme point de référence de l'axe horizontal) : la séquence Do Ré Mi Fa Sol La Si La Sol Fa engendre la séquence inverse Do Sib Lab Sol Fa Mib Réb Mib Fa Sol.
- La rétrograde du renversement (D), qui consiste à combiner ces deux procédés. Exemple (voir Figure ci-dessus) : la combinaison des deux exemples précédents engendre la séquence Sol Fa Mib Réb Mib Fa Sol Lab Sib Do.
Attention : le renversement palindromique (C) est différent du renversement d'un intervalle ou d'un accord en musique.
Selon les compositeurs, les morceaux A, B, C et D peuvent êtres mixés en séquence ou en superposition. Par exemple :
Chez Guillaume de Michaut ("Ma fin est mon commencement") : superposition A + B, où la voix du Ténor fait partie intégrante de A.
Chez J.S. Bach (Offrande musicale, canon cancrizans ou canon per motum contrarium) : superposition A + B ou parfois superposition A + D
Chez Haydn (symphonie n°47, menuet du Palindrome) : séquence A puis B puis C puis superposition A + D
B5.11. Sources :
[AMB] Wikipedia - Ambigramme
[DEL] Jean-Paul Delahaye, Ambigrammes, revue Pour la Science, N° 323, Septembre 2004
[DUR] Gérard Durand, Palindromes en folie
[PAL] The Palindrome, Palindrome ?
[QUI] Quillbot, Palindromes
[RED] reddit, Quelle est la plus grande ville du monde qui porte un nom palindromique ?
[STA] StarinuX, Liste de palindromes
[VIL] Gérard Villemain, Langue - Palindromes - Villes
[VIL] Gérard Villemain, Formes- Palindromes - Introduction
[VIL] Gérard Villemain, Formes - Palindromes - Dates
[VIL] Gérard Villemain, Formes- Palindromes - Carrés
[VIL] Gérard Villemain, Formes- Palindromes - Cubes
[WIK] Wikipedia, Palindrome
[WIK] Wikipedia, Liste des palindromes en français
[WIK] Wikipedia, Palindrome (multilangues)
Voici une collection de tours de magie spectaculaires.
Sommaire :
B6.1. Tours de magie avec cordes ou élastiques :
Voici quelques tours spectaculaires utilisant des cordes, des élastiques ou rien que les mains.
B6.1.1. Mains retournées :
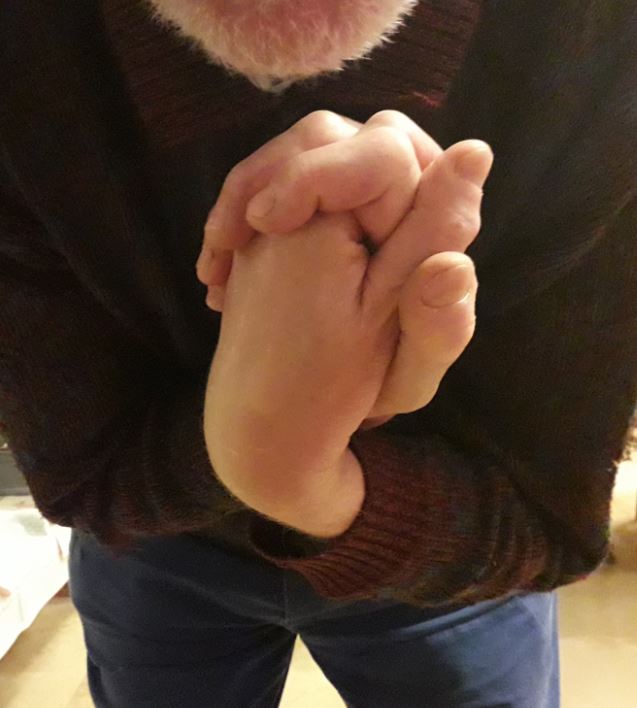
Ce tour est une expérience de psychologie cognitive populaire.
On demande à un spectateur de croiser les bras, de joindre les deux mains, paume contre paume, en entrelaçant les doigts, puis de retourner l'ensemble en le remontant par l'intérieur.
Cette position un peu inconfortable expose alors les deux rangées de doigts vers le haut (voir Figure ci-dessus).
On désigne alors un doigt spécifique sans le toucher, et on demande au spectateur de le lever vite et sans réfléchir.
Le spectateur lève alors fréquemment le doigt symétrique opposé.
Cette erreur vient d'un conflit entre une représentation interne des doigts, perturbée par la posture inhabituelle, et les commandes motrices automatiques, prévues pour des mains en position normale. La vision pourrait corriger, mais pas assez vite lorsqu'on demande une réponse immédiate.
B6.1.2. Echange de piles entre deux mains :

Ce tour de dextérité consiste à échanger deux piles rondes AA d'une main à l'autre, sans lâcher les piles ni utiliser de trucage.
La manipulation est simple et rapide, mais difficile à reproduire par le spectateur.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [PRA][ASH]) :
1. Tenir dans chaque main une pile ronde AA au creux du pouce et de l'index, la pile étant pincée en son milieu, un peu inclinée vers le poignet et cul (pole négatif) vers la paume.
2. Mettre les mains face au spectateur, paumes cachées, en position tête-bêche, doigts à l'horizontale et dans un plan vertical.
3. Tourner la main droite d'un quart de tour dans le sens anti-horaire.
4. Rapprocher les deux mains l'une de l'autre, en gardant les doigts parallèles, le pouce droit venant glisser sous le pouce gauche.
5. Poser chaque pouce sur le cul de chaque pile et boucler avec chaque majeur venant se poser sur l'autre extrémité des piles (pole positif).
6. Pincer chaque pile entre pouce et majeur, puis écarter doucement chaque main.
7. Tourner légèrement les deux mains sur elles-mêmes afin de présenter au spectateur les deux piles en position verticale.
8. Ramener les piles en position initiale (étape 1) en inversant les étapes.
A noter : Au lieu de pincer les piles entre pouce et majeur, on peut aussi le faire entre pouce et index (comme montré sur la Figure ci-dessus), mais cette position de doigts lors du bouclage croisé (étape 5) est plus forcée et moins confortable.
B6.1.3. La bague voyageuse :

1. Ce tour spectaculaire nécessite une bague (ou un anneau) et un élastique coupé, de longueur 10 cm environ et de couleur pas trop voyante (voir Figure ci-dessus, cf. [MIR]).
2. Enrouler l'élastique dans votre main gauche en laissant dépasser de 1 cm environ l'extrémité, la pincer fermement entre pouce et index, puis passer l'élastique dans la bague.
3. Saisir l'élastique entre pouce et index de la main droite, le tendre au maximum et en l'inclinant légèrement vers le haut. La bague vient buter naturellement contre la main gauche.
4. Sans bouger aucune main, la bague se met alors à monter doucement le long de l'élastique.
Solution : après tension de l'élastique, le laisser filer doucement entre pouce et index de la main gauche, ce qui fait monter la bague.
B6.1.4. Elastique sauteur entre doigts :
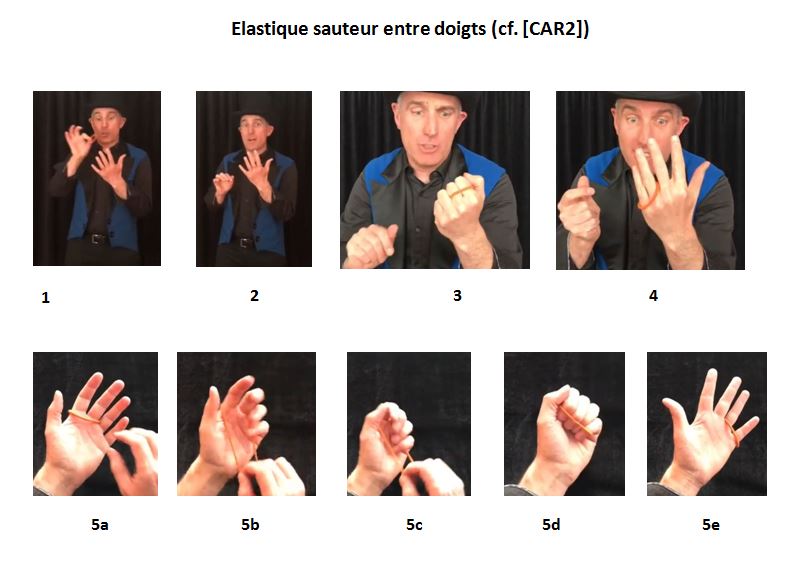
Ce tour de magie nécessite un petit élastique de couleur voyante.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [CAR2]) :
1. Face au spectateur, présenter l'élastique au-dessus d'une main verticale.
2. Passer l'élastique autour de l'index et du majeur de cette main.
3. Coller doigts et pouce contre l'élastique et fermer le poing en le disant.
4. Souffler sur les doigts et réouvrir le poing. L'élastique saute soudainement et vient entourer les deux autres doigts.
Explications : juste avant la fermeture du poing, saisir l'élastique entre le pouce et l'index de l'autre main (5a), le-tirer rapidement vers le bas jusqu'en bas de paume (5b), fermer le poing (5c), déposer l'élastique à la base des quatre ongles des doigts, en allant de l'auriculaire à l'index (5d). Puis ouvrir le poing (5e).
Amélioration : pour mieux cacher cette manipulation secrète, avant la fermeture du poing, saisir l'élastique, le tirer en arrière avec l'index en plaquant la paume sur le poignet, pouce et autres doigts face au spectateur, fermer le poing, baisser les bras sous la table, déposer l'élastique sur les doigts, reformer le placage au poignet, remontrer l'ensemble inchangé au spectateur. Puis ouvrir le poing.
B6.1.5. Elastique sauteur entre mains :
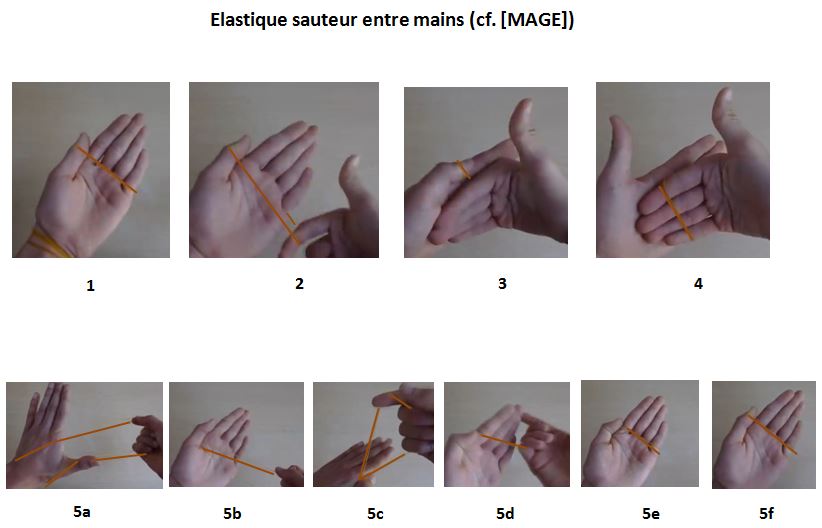
Ce tour de magie nécessite deux élastiques de même couleur et assez longs.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [MAGE]) :
1. Présenter votre paume ouverte au spectateur, avec un élastique entourant le haut du pouce et la base des quatre autres doigts.
2. Avec l'index de l'autre main, décoller l'élastique tout autour de la main pour bien montrer que l'élastique est normal.
3. Présenter l'autre main en position tête-bêche, et tapoter doigts contre doigts.
4. Lever le pouce. L'élastique saute soudainement sur les quatre doigts de l'autre main.
Solution : préparer l'élastique comme suit :
5a. Passer l'élastique autour du poignet, côté paume de la main, puis au creux entre pouce et index.
5b. Serrer fortement le pouce contre l'index pour coincer l'élastique, puis retourner la main, paume vers le haut.
5c. Faire passer l'élastique entre haut du pouce et index en maintenant la pression.
5d. Retourner la main, paume vers le bas, puis passer la boucle de l'élastique autour des quatre doigts.
5e. Retourner à nouveau la main, paume vers le haut, l'élastique se trouvant à la base des quatre doigts.
5f. Tirer un peu l'élastique pour le faire passer au-dessus du haut du pouce.
5g. Porter un second élastique autour du poignet pour camoufler la préparation secrète.
La préparation est maintenant achevée et le tour peut commencer devant un spectateur.
B6.1.6. Elastiques entremêlés :

Ce tour de magie nécessite deux petits élastiques identiques et de même couleur.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [JER]) :
1. Tenir un élastique verticalement entre le pouce et l'index de la main gauche, et un autre entre pouce et majeur de la main droite, les deux élastiques étant entremêlés.
2. Manoeuvrer les deux mains en les rapprochant/éloignant et aussi en les faisant pivoter en sens inverse, pour montrer au spectateur que le système est bloqué.
3. Ecarter les mains soudainement. Les deux élastiques se trouvent libérés.
Solution :
4a. Au moment du pivotement des mains, passer l'index droit, qui est libre, dans la boucle du pouce droit.
4b. Enfoncer l'index droit et le passer derrière l'élastique de gauche.
4c. Retirer le majeur droit de l'élastique de droite.
4d. L'élastique passe automatiquement sur l'index droit.
4e. Recoller immédiatement l'élastique contre l'autre, afin de simuler le blocage.
4f. Ecarter les mains soudainement.
Solution améliorée (cf. [PAU][VAL]) :
A l'étape 1, tenir l'élastique horizontalement (et non verticalement), ce qui évite le passage derrière l'élastique de gauche à l'étape 4b.
B6.1.7. Les lacets fous :
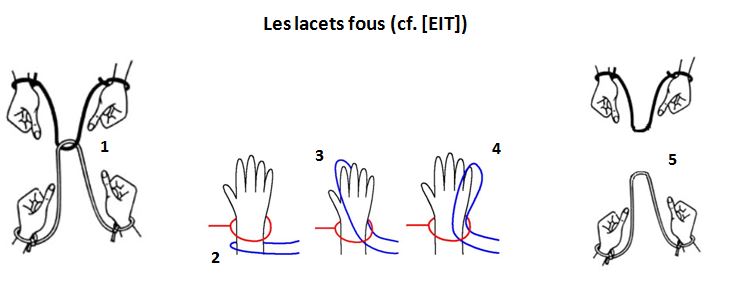
Ce tour spectaculaire est le suivant :
1. Deux personnes sont debout face à face (voir Figure ci-dessus, cf. [EIT]).
Chacune a les poignets reliés par une corde d'environ 1 mètre, formant une boucle peu serrée autour de chaque poignet et fermée par un noeud supposé indémontable.
Les deux cordes sont entrelacées, ce qui relie les deux personnes.
Comment peuvent-elles se séparer sans couper la corde, sans défaire les noeuds et sans faire glisser la corde le long des mains ?
Solution :
2. Faire une Ganse (boucle ouverte en forme de U allongé) avec sa propre corde derrière la corde du partenaire.
3. Passer la Ganse à travers la boucle entourant le poignet du partenaire, en allant du bras vers les doigts.
4. Passer la Ganse par-dessus la main du partenaire.
5. Tirer sur la corde : celle-ci se dégage miraculeusement et les deux personnes se trouvent alors complètement séparées.
B6.1.8. Evasion avec mains liées :
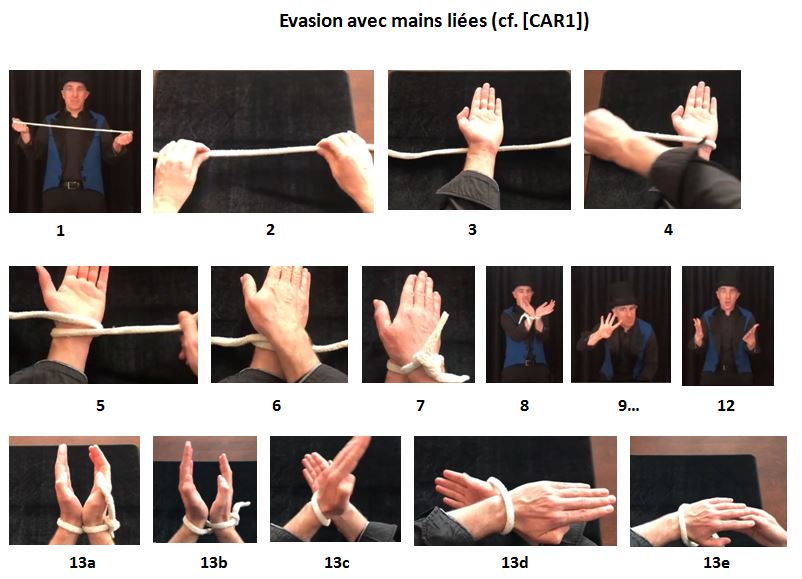
Ce tour de magie nécessite seulement une corde de 70 cm de long environ.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [CAR1]) :
1. Placer une table entre vous et le spectateur, et montrer une "corde bien solide" tendue entre vos deux mains.
2. Poser la corde sur la table, parallèle au spectateur.
3. Poser votre main gauche au milieu de la corde, paume vers le haut.
4. Faire passer le brin droit de la corde, à gauche par-dessus le poignet, et devant le brin gauche.
5. Faire passer le brin gauche de la corde à droite par-dessus le poignet, sans croiser l'autre brin.
6. Poser la main droite sur la main gauche, paume vers le dessous.
7. Demander au spectateur de prendre les deux brins libres et de les nouer au dessus des mains par trois noeuds successifs bien serrés.
8. Lever vos bras en montrant vos deux mains bien attachées.
9. Descendre vos mains derrière la table puis aussitôt... ressortir votre main droite libre.
10. Redescendre la main libre derrière la table puis aussitôt... ressortir à nouveau les deux mains attachées.
11. Recommencer une nouvelle fois la séquence 9 à 10.
12. Descendre vos mains derrière la table puis aussitôt... ressortir les deux mains libérées.
Explications : derrière la table, faire un quart de tour en sens inverse à chaque poignet (13a, 13b, 13c, 13d) et retirer la main droite de la boucle (13e). Inverser la manoeuvre pour réattacher les deux mains ensemble.
A noter : une version plus sophistiquée de ce tour existe (voir [HAF]).
B6.2. Tours de magie avec cartes à jouer :
Voici quelques tours spectaculaires utilisant des cartes à jouer et réalisables par des enfants.
B6.2.1. Les valets voleurs :

Ce tour nécessite un jeu de 32 cartes :
1. Sortir trois valets d'un jeu de cartes et laisser le paquet retourné sur la table (faces cachées).
2. Raconter l'histoire : "Trois voleurs veulent s'introduire dans une maison...
3. Le premier trouve un soupirail et passe par la cave (mettre un valet sous le paquet).
4. Le second monte sur le toit et passe par le grenier (mettre un valet sur le paquet).
5. Le troisième trouve une fenêtre ouverte et passe au rez-de-chaussée (insérer un valet dans le paquet)".
6. Demander au spectateur de "couper" le paquet.
7. Annoncer que les trois valets vont se retrouver ensemble et étaler le jeu en éventail pour le vérifier.
Solution : Préparer le paquet en mettant un valet (le quatrième) sur le dessus. Les trois valets réunis à la fin du tour ne sont pas les mêmes mais cela échappe souvent au spectateur.
B6.2.2. Les quatre rois :

Ce tour est une variante du tour "Les trois voleurs". Il nécessite un jeu de 32 cartes :
1. Présenter les quatre rois en éventail devant le spectateur.
2. Les empiler sur le dessus du paquet restant.
3. Reprendre une à une les quatre cartes du dessus et les insérer dans le paquet.
4. Demander au spectateur de "couper" le paquet en deux parties approximativement égales.
5. Annoncer que les quatre rois vont se retrouver ensemble et étaler le jeu en éventail pour le vérifier.
Solution : avant de commencer le tour, rajouter discrètement une pile de quatre cartes quelconques sous l'éventail des quatre rois, bien cachée par le premier roi (voir Figure ci-dessus).
B6.2.3. Les quatre as :

Ce tour nécessite un jeu de 32 cartes :
1. Donner au spectateur un jeu de cartes pour battre, puis reprendre le jeu et présenter-le verticalement, face au spectateur.
2. Demander-lui de prendre un des as et de le mettre contre sa poitrine, face bien cachée.
3. Passer le jeu derrière votre dos, puis remontrer le jeu au spectateur en lui demandant de replacer son as dans le jeu.
4. Redonner au spectateur le jeu de cartes pour battre, puis reprendre le jeu et sortir l'as choisi.
Solution :
- Préparer le jeu de cartes en mettant la "pointe" de chaque as situé au centre de la carte selon la même orientation (pique, coeur, trèfle), l'as de carreau étant symétrique (voir Figure ci-dessus).
- Derrière votre dos, tourner le jeu de cartes d'un demi-tour (haut/bas inversés).
- L'as choisi est l'as de carreau si aucune "pointe" n'est inversée, et l'as à "pointe" inversée dans le cas contraire.
- Attention : sortir du paquet l'as choisi, pouce dirigé vers soi, puis présenter la carte au spectateur, pouce dirigé vers lui (ce qui inverse le sens de la carte afin de pouvoir refaire le tour). Remettre ensuite la carte dans le paquet, pouce dirigé vers le spectateur
A noter : au niveau des figures (valet, dame, roi et joker), des cartes numériques (de l'as au dix) et des éventuels index disposés en coins opposés, les jeux de 54 cartes français standards post-19e siècle présentent généralement des cartes symétriques par rotation d'un demi-tour. Il existe 18 exceptions : les deux Joker (rouge et noir), les quatre "sept" (un par couleur) et quatre triplets de cartes (pique, coeur, trèfle) correspondant aux as, trois, cinq et neuf.
B6.2.4. La carte retrouvée :

Ce tour est une généralisation spectaculaire et peu connue du tour "Les quatre as". Il nécessite un jeu de 32 cartes :
1. Donner au spectateur un jeu de cartes pour battre, puis reprendre le jeu et présenter-le verticalement, face au spectateur.
2. Demander-lui de prendre une carte quelconque et de la mettre contre sa poitrine, face bien cachée.
3. Passer le jeu derrière votre dos, puis remontrer le jeu au spectateur en lui demandant de replacer sa carte dans le jeu.
4. Redonner au spectateur le jeu de cartes pour battre, puis reprendre le jeu, présenter-le en éventail, faire défiler les cartes une par une rapidement et sortir la carte choisie.
Solution :
- Tout jeu de carte n'est pas parfaitement imprimé au milieu de chaque carte. Le bandeau blanc séparant le bord supérieur de la carte et le haut de sa partie imprimée (petit côté du rectangle entourant chaque figure, ou tête de chaque nombre) n'est pas identique entre le haut et le bas de la carte. Sauf exception, chaque carte possède donc un petit bandeau et un grand bandeau.
- Préparer le jeu de cartes en mettant le petit bandeau partout du même côté. Si le bandeau est quasi-identique entre haut et bas de carte, éliminer la carte du paquet.
- Derrière votre dos, tourner le jeu de cartes d'un demi-tour (haut/bas inversés).
- Lors du défilement des cartes, viser le bandeau du haut. La carte choisie est celle dont le bandeau change subitement de taille (petit/grand) par effet stroboscopique.
- Attention : sortir du paquet la carte choisie, pouce dirigé vers soi, puis présenter la carte au spectateur, pouce dirigé vers lui (ce qui inverse le sens de la carte afin de pouvoir refaire le tour). Remettre ensuite la carte dans le paquet, pouce dirigé vers le spectateur.
B6.2.5. Mémorisation magique :

Ce tour spectaculaire nécessite un jeu de 32 cartes :
1. Battre le jeu de cartes.
2. Passer le jeu derrière votre dos, faire passer la carte du dessous sur le dessus du jeu et présenter verticalement le jeu au spectateur, du côté de cette carte.
3. Annoncer la carte et recommencer à l'étape 2.
4. Continuer ainsi avec toutes les cartes du paquet.
Solution :
- A la fin du battage des cartes, mémoriser discrètement la dernière carte sur le dessous du paquet.
- Pendant la présentation du jeu au spectateur, mémoriser la carte du dessous qui vous fait face.
B6.2.6. Le tour des 27 cartes :
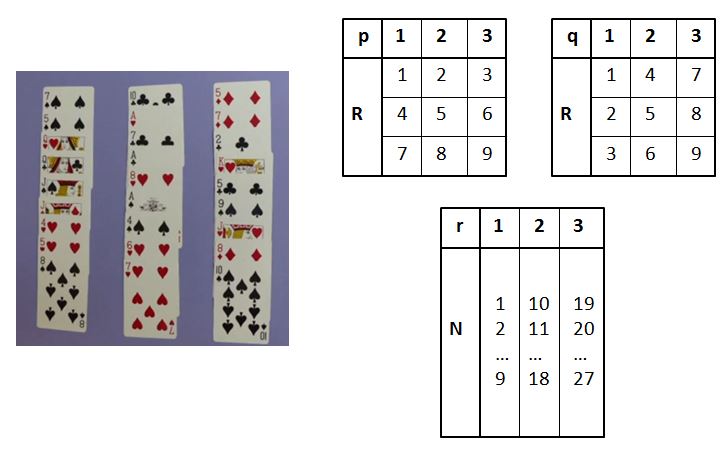
Ce tour purement mathématique nécessite un jeu de 32 cartes :
1. Faire un paquet de 27 cartes exactement.
2. Présenter au spectateur le paquet en éventail. Demander-lui de retenir mentalement une carte C, puis de donner un nombre N de 1 à 27. Calculer secrètement le nombre R = N - multiples de 9, en ajustant R entre 1 et 9 (exemples : si N = 18, alors R = 9 ; si N = 22, alors R = 4).
3. Retourner le paquet, faces cachées, et former trois colonnes de neuf cartes chacune, en retournant les cartes sur la table, faces visibles, par rangées horizontales de trois cartes, de gauche à droite, et de haut en bas (voir Figure ci-dessus).
4. Demander au spectateur de désigner la colonne dans laquelle se trouve sa carte, puis empiler les cartes, faces visibles et colonne par colonne, en ramassant la colonne désignée en position p = R - multiples de 3, en ajustant p entre 1 et 3 (exemple : si R = 4, alors p = 1). Plus simplement, la colonne p se "voit" immédiatement sans aucun calcul en répartissant R dans un carré 3x3, par rangées horizontales de 3, de gauche à droite, et de haut en bas (voir Figure ci-dessus).
5. Retourner le paquet et former à nouveau trois colonnes de neuf cartes chacune, comme précédemment, et redemander la colonne. Empiler les cartes, faces visibles et colonne par colonne, en ramassant la colonne désignée en position q = 1 + Ent[(R - 1)/3] (exemple : si R = 4, alors q = 2). Plus simplement, la colonne q se "voit" immédiatement sans aucun calcul en répartissant R dans un carré 3x3, par colonnes verticales de 3, de haut en bas, et de gauche à droite (voir Figure ci-dessus).
6. Retourner le paquet et former à nouveau trois colonnes de neuf cartes chacune, comme précédemment, et redemander la colonne. Repérer la carte C située dans cette colonne en position R. Empiler les cartes, faces visibles et colonne par colonne, en ramassant la colonne désignée en position r = 1 + Ent[(N - 1)/9] (exemple : si N = 22, alors r = 3). Plus simplement, la colonne r se "voit" immédiatement sans aucun calcul en répartissant N dans un rectangle 9x3, par colonnes verticales de 9, de haut en bas, et de gauche à droite (voir Figure ci-dessus).
7. Retourner le paquet et poser les cartes une à une sur la table, faces cachées, en comptant à partir de 1. A la Nème carte, annoncer la carte C et la retourner.
Démonstration :
Soit p, q et r les numéros d'ordre (entre 1 et 3) de ramassage de la colonne désignée, à chaque étalage des cartes en trois colonnes.
Soit Np, Nq et Nr la position dans le paquet (entre 1 et 27) de la première carte du bloc contenant la carte C, après avoir ramassé la colonne désignée p, q ou r, et reformé le paquet.
A chaque étalage, on ne détermine pas la position exacte de la carte C dans le paquet, mais la position de la première carte du bloc qui la contient. La taille de ce bloc est divisée par 3 à chaque étape.
Au premier étalage, le paquet de 27 cartes est divisé en 3. Après avoir ramassé la colonne p et reformé le paquet, la carte C se trouve mécaniquement dans un bloc continu de 9 cartes, dont la position de la première carte vaut :
Np = 1 + 9(p - 1), correspondant à l'intervalle Ip = [Np, Np + 8].
Exemples :
si p = 1, Ip = [1, 9].
Si p = 2, Ip = [10, 18].
Si p = 3, Ip = [19, 27].
Au second étalage, ce bloc de 9 cartes est divisé en 3. Après avoir ramassé la colonne q et reformé le paquet, la carte C se trouve mécaniquement dans un bloc continu de 3 cartes, dont la position de la première carte vaut :
Nq = 9(q - 1) + 1 + (Np - 1)/3 = 1 + 9(q - 1) + 3(p - 1), correspondant à l'intervalle Iq = [Nq, Nq + 2].
Exemples :
si p = 1 et q = 1, Iq = [1, 3].
Si p = 1 et q = 2, Iq = [10, 12].
Si p = 2 et q = 1, Iq = [4, 6].
Si p = 2 et q = 2, Iq = [13, 15]
Si p = 3 et q = 1, Iq = [7, 9]
Au troisième étalage, ce bloc de 3 cartes est divisé en 3. Après avoir ramassé la colonne r et reformé le paquet, la carte C se trouve mécaniquement dans un bloc de 1 seule carte, dont la position vaut :
Nr = 9(r - 1) + 1 + (Nq - 1)/3 = 1 + 9(r - 1) + 3(q - 1) + (p - 1), correspondant à l'intervalle Ir = [Nr, Nr].
Exemples :
si p = 1, q = 1 et r = 1, Ir = [1, 1].
Si p = 1, q = 1 et r = 2, Ir = [10, 10].
Si p = 1, q = 2 et r = 1, Ir = [4, 4].
Si p = 1, q = 2 et r = 2, Ir = [13, 13].
Si p = 2, q = 1 et r = 1, Ir = [2, 2].
Si p = 2, q = 1 et r = 2, Ir = [11, 11].
Si p = 2, q = 2 et r = 1, Ir = [5, 5].
Si p = 2, q = 2 et r = 2, Ir = [14, 14].
Si p = 3, q = 1 et r = 1, Ir = [3, 3].
Compte tenu de l'expression de Nr, le nombre N en fin de tour vérifie donc la formule : N - 1 = 9(r - 1) + 3(q - 1) + (p - 1)
Ce tour n'est donc qu'un décodage du nombre (N - 1) en base 3, colonne par colonne, où chaque choix de colonne fournit un des trois chiffres ternaires.
Compte tenu de cette formule, les expressions simplifiées de p, q et r sont alors les suivantes :
On pose R = (N - 1) mod 9 + 1 = N - multiples de 9, en ajustant R entre 1 et 9
p = (N - 1) mod 3 + 1 = (R - 1) mod 3 + 1 = R - multiples de 3, en ajustant p entre 1 et 3 = colonne du carré p(R) en Figure ci-dessus.
q = Ent[(N - 1)/3] mod 3 + 1 = Ent[(R - 1)/3] + 1 = colonne du carré q(R) en Figure ci-dessus.
r = Ent[(N - 1)/9] + 1 = colonne du rectangle r(N) en Figure ci-dessus.
B6.2.7. Le bonneteau :
Le bonneteau est un jeu de cartes pratiqué dans la rue, où un joueur doit retrouver la carte rouge parmi trois cartes après un mélange rapide.
Le matériel requis est le suivant :
- une tablette rigide ou un carton épais servant de table.
- trois cartes : deux noires (par exemple : le roi de pique et le roi de trèfle) et une rouge (la dame de coeur).
- de l'argent liquide pour les mises du joueur.
Le bonneteur est un manipulateur professionnel. Il présente le jeu, mélange les cartes et dirige la partie.
Le joueur mise une somme d'argent et désigne la carte qu'il pense être la rouge.
Les barons sont les complices du bonneteur. Ils font semblant de jouer et de gagner pour inspirer confiance, attirent les passants, surveillent la police et apaisent les perdants.
En France, le bonneteau est interdit, car il s'inscrit dans un jeu de hasard réalisé sur la voie publique avec mise d'argent (article L. 324-1 du Code de la sécurité intérieure).
Règles du jeu :
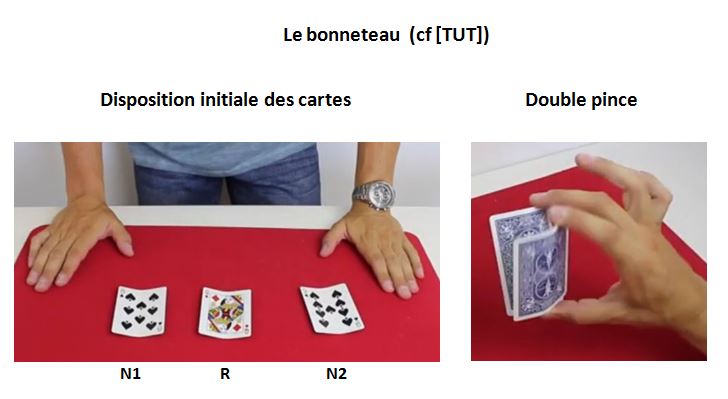
1. Le bonneteur montre les trois cartes, faces visibles, et place la rouge entre les deux noires. Les cartes sont légèrement pliées dans le sens de la longueur pour mieux les saisir par les bords courts quand elles sont faces cachées (voir Figure 1 ci-dessus [TUT]).
2. Il retourne les cartes, faces cachées, et les mélange rapidement sur la table par des mouvements linéaires.
3. Le bonneteur retourne la carte du milieu qui n'a pas changé (rouge). Il la retourne à nouveau et fais un second mélange apparemment identique au premier.
4. Le joueur mise alors une somme d'argent et désigne la carte (gauche, centre, droite) qu'il pense être la rouge.
5. Le bonneteur retourne la carte désignée. Si c'est la rouge, le joueur reçoit le double de sa mise. Sinon, la mise est perdue.
Mais en pratique, le jeu est truqué :
1. Le bonneteur commence souvent par quelques manches honnêtes et lentes, où les barons gagnent facilement pour mettre le public en confiance.
2. Dès qu'un vrai joueur participe, le bonneteur modifie ses manipulations :
- Lancer par rotation d'index : prise spécifique à deux cartes pour permettre un lancer indépendant de la carte supérieure ou inférieure. Cette technique "double pince" est idéale pour les mélanges prolongés.
- Filage : glisse discrète d'une carte sous une autre.
- Echange rapide : permutation dissimulée de deux cartes au moment de la pose.
3. Résultat : Le bonneteur garde à tout moment le contrôle de la position réelle de la rouge.
Technique de lancer par rotation d'index [TUT] :
La technique de lancer par rotation d'index consiste à relâcher discrètement la carte supérieure (noire) tout en retenant la carte inférieure (rouge).
- Position initiale : La carte supérieure (noire) est tenue entre pouce et index au niveau des deux coins. La carte inférieure (rouge) est tenue de façon identique mais entre pouce et majeur. Les deux cartes partagent un point d'appui commun au niveau du pouce, tandis qu'un petit espace en forme de coin existe entre leurs bords opposés (voir Figure 2 ci-dessus [TUT]).
- Exécution : On retourne le poignet pour montrer clairement la rouge au joueur et on se replace paume tournée vers la table. Ensuite, pendant le mouvement linéaire au-dessus de la table, l'index effectue une rotation nette mais discrète, libérant la pression exercée sur la carte supérieure (noire). Celle-ci glisse alors passivement vers l'avant, tandis que le pouce/majeur maintiennent fermement la carte inférieure (rouge).
- Fin du mouvement : La carte lancée semble suivre le continuïté du mélange et être toujours la carte inférieure.
- Double lancer à une main [TUT, 04:20] :
- La disposition initiale des cartes sur la table, vue du joueur, est N1 R N2 (avec N = noire et R = rouge).
- Deux cartes sont prises en double pince, d'abord N1 en carte supérieure, puis R en carte inférieure. On retourne le poignet pour montrer clairement R au joueur.
- On effectue un premier lancer de la carte (N1) en la posant au milieu puis la carte restante (R) à gauche, ce qui transforme secrètement la disposition en R N1 N2.
- Deux autres cartes sont prises ensuite en double pince, d'abord R en carte supérieure, puis N2 en carte inférieure. On retourne le poignet pour montrer clairement N2 au joueur.
- On effectue un second lancer de la carte (R) en la posant à droite puis la carte restante (N2) à gauche, ce qui transforme secrètement la disposition en N2 N1 R.
- Le joueur est doublement piégé, en pensant que R se trouve soit au milieu, soit à gauche.
Technique de mélange :
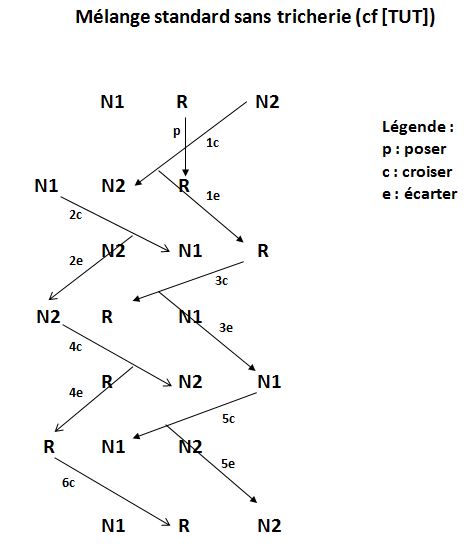
La technique standard de mélange s'exécute sur trois temps rythmés (voir Figure 3 ci-dessus et [TUT, 03:58]) :
- Temps 1 : Pose centrale. Poser au milieu l'une des deux cartes tenues en double pince en utilisant la technique de lancer par rotation d'index.
- Temps 2 : Cinq séquences successives Croiser-Ecarter :
- Le Croiser consiste à faire passer une carte par-dessus celle située immédiatement à sa gauche (resp. à sa droite).
- L'Ecarter consiste à déplacer une carte extérieure vers la droite (resp. vers la gauche) en créant une place vide temporaire destinée à recevoir une autre carte.
- Les cinq séquences alternent systématiquement de côté (Gauche et Droite) selon le schéma binaire : Croiser G - Ecarter D | Croiser D - Ecarter G | Croiser G - Ecarter D | Croiser D - Ecarter G | Croiser G - Ecarter D
- Temps 3 : Croiser final. Croiser une dernière fois à Droite.
Lorsque le mélange est exécuté sans tricherie, avec lancer de la carte inférieure (rouge), la disposition initiale N1 R N2 des trois cartes reste inchangée en final, ce qui renforce l'illusion de neutralité du procédé.
B6.3. Tours de magie avec nombres :
Voici quelques tours spectaculaires utilisant des nombres.
B6.3.1. Lecture de pensée :
[raconté par Clément Brizzard]
Ce tour spectaculaire est une expérience magique de lecture de pensée.
Le magicien demande à une personne de l'auditoire de penser à un nombre entier entre 1 et 100,
puis de le multiplier par 9, puis de retrancher 5, puis de faire la somme des chiffres du nombre obtenu,
puis de recommencer cette dernière opération si le résultat est supérieur à 9,
puis de convertir le résultat obtenu en une lettre de l'alphabet : A pour 1, B pour 2, C pour 3, etc.,
puis de penser (en français) à un pays d'Europe commençant par cette lettre,
puis de penser (en français) à un fruit commençant par la dernière lettre du pays d'Europe.
Le magicien annonce alors que le fruit pensé est un "kiwi". Si la personne dit que cela est faux, alors le magicien annonce que le fruit est un "kaki".
A aucun moment, la personne n'a parlé.
Explication :
Tout nombre entier N à n chiffres est de la forme cn...c2c1 et peut s'écrire :
N = 10n - 1 cn + ... + 100 c3 + 10 c2 + c1 = (10n - 1 - 1) cn + ... + 99 c3 + 9 c2 + (cn + ... + c3 + c2 + c1)
Donc N est de le forme : N = 9 K + somme S des chiffres de N
Si S est supérieur à 9, alors on a de même : S = 9 K' + somme S' des chiffres de S
En final, tout nombre N est donc toujours la somme d'un multiple de 9 et d'un reste compris entre 1 et 9 correspondant à la somme simple ou répétée des chiffres du nombre N.
Exemple 1 : 8 = 9 x 0 + 8, 8 étant le chiffre même du nombre 8.
Exemple 2 : 34 = 9 x 3 + 7, 7 étant la somme 3 + 4 des chiffres du nombre 34.
Exemple 3 : 38 = 9 x 4 + 2, 2 étant la somme 3 + 8 = 11 des chiffres de 38, puis la somme 1 + 1 des chiffres de 11
Si N est déjà un multiple de 9 (comme demandé par le magicien), alors ce reste vaut nécessairement 9.
Si on retranche 5 de ce N multiple de 9, alors ce reste vaut 4.
Le seul pays d'Europe commençant par la lettre D (correspondant à 4 dans l'alphabet) est le "Danemark" (en français).
Les seuls fruits courants commençant par un K (correspondant à la dernière lettre du mot "Danemark") sont le "kiwi" et le "kaki" (en français).
D'où la réponse du magicien, sans aucune lecture de pensée.
Améliorations du tour :
- Proposer de choisir N entre 1 et 10 plutôt qu'entre 1 et 100.
- Multiplier N par 10 puis retrancher N, plutôt que multiplier N par 9.
- On peut refaire le tour une seconde fois, mais avec une autre personne, et avec la modification suivante : ne pas demander un pays d'Europe mais directement un fruit commençant par la lettre de l'alphabet (ce qui donne la "Datte" correspondant au résultat 4 = D).
- On peut refaire le tour une troisième fois avec une personne quelconque, en demandant de retrancher 7 et non 5. Ensuite, ne pas demander un pays d'Europe mais directement un fruit commençant par la lettre de l'alphabet (ce qui donne la "Banane" correspondant au résultat 2 = B).
B6.3.2. L'âge des enfants :
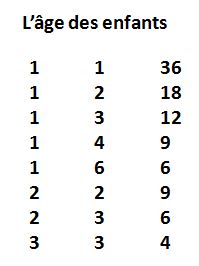
Un père de famille parle au facteur : "J'ai trois enfants. Le produit de leur âge est égal à 36. La somme de leur âge est égal au numéro de la maison en face."
Le facteur regarde ce numéro et demande : "Il me manque une donnée pour résoudre le problème."
Le père répond : "En effet. Mon aîné est blond."
Le facteur donne alors la solution. Comment a-t-il fait ?
Solution de cette énigme :
On peut obtenir 36 de 8 manières différentes :
1 x 1 x 36 dont la somme est 38
1 x 2 x 18 dont la somme est 21
1 x 3 x 12 dont la somme est 16
1 x 4 x 9 dont la somme est 14
1 x 6 x 6 dont la somme est 13
2 x 2 x 9 dont la somme est 13
2 x 3 x 6 dont la somme est 11
3 x 3 x 4 dont la somme est 10
Le facteur ne pouvant pas conclure en voyant le numéro de la maison en face, cela indique que la somme donne plusieurs possibilités et non une seule.
Il n'y a que 13 qui est ambigue et vu qu'il n'y a qu'un seul ainé, les enfants ont donc 2, 2 et 9 ans.
B6.3.3. Le tour de Maurice Dagbert :

[entendu à la radio dans les années 1980]
Un célèbre calculateur prodige français, Maurice Dagbert, a présenté ce problème apparemment impossible :
"Choisissez un nombre entier entre 1000 et 3000 [2139 fut donné]. Je vais calculer maintenant deux listes de 17 nombres entiers chacune, telles que :
- Les sommes des nombres sont égales à 2139,
- Les sommes des carrés des nombres sont égales,
- Les sommes des cubes des nombres sont égales,
et ainsi de suite jusque la puissance sixième des nombres.
De plus, tous les nombres seront différents entre eux, que ce soit dans une liste ou entre listes."
Pour le nombre N = 2139 choisi, il énonça alors, au bout de quelques minutes seulement, les deux listes suivantes :
Première liste (La) = [ 59, 63, 68, 82, 86, 100, 105, 109, 139, 143, 148, 156, 162, 173, 175, 185, 186 ]
Seconde liste (Lb) = [ 60, 61, 70, 79, 89, 98, 107, 108, 140, 141, 151, 153, 164, 170, 178, 183, 187 ]
Un ordinateur confirma les calculs.
L'explication est la suivante :
1. Modélisation mathématique :
Le problème s'écrit sous forme du système d'équations S suivant, avec k = 6, n = 17 et Somme = N.
(1) Système S :
∑iai = ∑ibi = Somme
∑iai2 = ∑ibi2
∑iai3 = ∑ibi3
...
∑iaik = ∑ibik
avec :
i = indice allant de 1 à n
n = taille de chaque liste
k = puissance des termes de la dernière équation
Somme = somme des termes de la première équation
ai et bi = nombres entiers positifs et tous distincts
2. Première astuce :
Chaque liste de 17 nombres est en fait une concaténation de deux sous-listes de 8 et 9 nombres chacune, vérifiant les sous-systèmes (S1) et (S2) suivants :
(21) Sous-système S1 = Système S pour k = 6, n = 8 et Somme = N1, correspondant aux listes partielles suivantes :
L1a = [ 59, 63, 68, 82, 86, 100, 105, 109 ]
L1b = [ 60, 61, 70, 79, 89, 98, 107, 108 ]
(22) Sous-système S2 = Système S pour k = 6, n = 9 et Somme = N2, correspondant aux listes partielles suivantes :
L2a = [ 139, 143, 148, 156, 162, 173, 175, 185, 186 ]
L2b = [ 140, 141, 151, 153, 164, 170, 178, 183, 187 ]
(23) Condition supplémentaire : N1 + N2 = N
3. Seconde astuce :
Chacun de ces sous-systèmes est connu en mathématique comme "Problème PTE (ou de Prouhet-Tarry-Escott)" [WIK1].
Ce problème a pour propriété remarquable d'être invariant par translation des variables [WIK1]. Si on remplace les variables ai et bi respectivement par (a*i = α ai - β) et (b*i = α bi - β), α et β étant deux constantes quelconques, alors les nouvelles variables sont solutions du même problème en modifiant seulement Somme par Somme* = (α Somme - n β)
Cette translation permet de normaliser les solutions, en imposant par exemple qu'elles soient positives et que le zéro y figure.
Pour S1, si on choisit α1 = 1 et β1 = 84, on obtient alors le sous-système translaté S1* comme suit :
(31) Sous-système S1* = sous-système S1 de somme N1* = N1 - 8 β1, correspondant aux listes translatées suivantes :
L1a* = [ -25, -21, -16, -2, 2, 16, 21, 25 ]
L1b* = [ -24, -23, -14, -5, 5, 14, 23, 24 ]
Cette solution, dite de taille paire et symétrique [WIK1], est de la forme [ -c4, -c3, -c2, -c1, c1, c2, c3, c4 ] pour la première liste et [ -d4, -d3, -d2, -d1, d1, d2, d3, d4 ] pour la seconde.
Cette symétrie rend automatiquement valides les équations en puissances impaires dans le sous-système S1*, ce qui se simplifie en :
Sous-système S1* :
n = 4
∑ici2 = ∑idi2
∑ici4 = ∑idi4
∑ici6 = ∑idi6
correspondant aux listes élémentaires suivantes :
C1 = [ ci ] = [ 2, 16, 21, 25 ]
D1 = [ di ] = [ 5, 14, 23, 24 ]
Pour S2, si on choisit α2 = 1 et β2 = 163, on obtient alors le sous-système translaté S2* comme suit :
(32) Sous-système S2* = sous-système S2 de somme N2* = N2 - 9 β2, correspondant aux listes translatées suivantes :
L2a* = [ -24, -20, -15, -7, -1, 10, 12, 22, 23 ]
L2b* = [ -23, -22, -12, -10, 1, 7, 15, 20, 24 ]
Cette solution, dite de taille impaire et symétrique [WIK1], est de la forme [ -c5, -c4, -c3, -c2, -c1, d2, d3, d4, d5 ] pour la première liste et [ -d5, -d4, -d3, -d2, c1, c2, c3, c4, c5 ] pour la seconde.
Cette symétrie rend automatiquement valides les équations en puissances paires dans le sous-système S2*, ce qui s'écrit :
Sous-système S2* :
n = 5
∑ici = ∑idi
∑ici3 = ∑idi3
∑ici5 = ∑idi5
avec d1 fictif = 0
correspondant aux listes élémentaires suivantes :
C2 = [ ci ] = [ 1, 7, 15, 20, 24 ]
D2 = [ di ] = [ 0, 10, 12, 22, 23 ]
Par ailleurs, la symétrie des solutions, pour chaque sous-système S1* et S2*, rend nulles les sommes N1* et N2*, ce qui se simplifie en :
(33) N1 = 8 β1 et N2 = 9 β2
Compte tenu de la relation (23), cela donne la condition nécessaire suivante :
(34) N = 8 β1 + 9 β2
A noter que cette condition est toujours possible à obtenir, vu que 8 et 9 sont premiers entre eux.
4. Choix d'une solution pour le sous-système S1* :
Le sous-système S1* (cf relations (31)) est celui du problème PTE de taille n = 4 et de puissances spécifiques k = 2, 4 et 6.
Plusieurs solutions sont connues depuis 1913, dont les suivantes [SHU1] :
[ 2, 16, 21, 25 ] = [ 5, 14, 23, 24 ]
[ 7, 24, 25, 34 ] = [ 14, 15, 31, 32 ]
[ 7, 31, 36, 50 ] = [ 18, 20, 41, 49 ]
[ 9, 47, 49, 67 ] = [ 23, 31, 61, 63 ]
La première solution est la plus petite solution en entiers non négatifs pour ces trois puissances [SHU2].
Il est fort probable que Maurice Dagbert connaissait ces solutions et a utilisé la première.
5. Choix d'une solution pour le sous-système S2* :
Le sous-système S2* (cf relations (32)) correspond au problème PTE de taille n = 5 et de puissances spécifiques k = 1, 3 et 5.
Les solutions publiées étant rares, elles peuvent cependant être trouvées analytiquement. La démarche consiste à apparier deux à deux les éléments des deux listes élémentaires, puis à résoudre le système quadratique obtenu par une méthode appropriée, comme celle par élimination des variables.
Ces deux approches reposent sur la résolution analytique d'un système quadratique sous-déterminé de rang 2 à 5 variables, produisant une famille de solutions réelles, complétée par une courte phase d'essais successifs ciblés visant à atteindre des valeurs entières vérifiant exactement les équations.
Les étapes sont les suivantes :
1. On fixe arbitrairement 5 valeurs δi entières petites (par exemple entre -3 et 3) telles que ∑i[δi] = 0 avec δi = ci - di
2. On pose xi = mi2 avec mi = (ci + di)/2 correspondant au centre local des variables ci et di, ce qui induit : xi # ci2 # di2 # ci di
où le symbole "#" signifie "très peu différent".
3. Compte tenu des identités : (c3 - d3) = (c - d)(c2 + c d + d2) et (c5 - d5) = (c - d)(c4 + c3 d + c2 d2 + c d3 + d4), les équations 2b deviennent :
∑ici - ∑idi = ∑i[δi] = 0
(∑ici3 - ∑idi3 # 3 ∑i[δi xi]) = 0
(∑ici5 - ∑idi5 # 5 ∑i[δi xi2]) = 0
4. Par l'une des méthodes évoquées ci-avant, on résout le système quadratique suivant :
(50) (∑i[δi xi] = 0) et (∑i[δi xi2] = 0)
ce qui donne une famille de solutions réelles pour xi.
Résolution par élimination des variables :
On fixe 3 variables libres, par exemple x1, x2 et x3
On élimine ensuite x4 entre les deux équations, ce qui donne une équation de la forme : A x52 + B x5 + C = 0, où A, B et C sont des polynômes quadratiques explicites en x1, x2 et x3, comme suit :
A = δ5 (δ4 + δ5)
B = 2 δ5 P
C = P2 + δ4 Q
avec P = ∑i=1,3[δi xi] et Q = ∑i=1,3[δi xi2]
On trouve les solutions réelles x5 = [-B ± √(B2 - 4 A C)]/(2 A) et x4 obtenu à partir de l'équation (∑i[δi xi] = 0).
5. On cherche des xi proches du carré d'un entier ou d'un demi-entier, ce qui donne ci = √xi + δi/2 et di = √xi - δi/2
6. On injecte les solutions entières ci et di dans les équations exactes (32) pour vérification.
7. En cas de non-vérification, on fait d'autres essais en modifiant le paramétrage à deux niveaux possibles :
- Exploration des 3 paramètres libres xi.
- Choix du vecteur des écarts δi.
Il est fort probable que Maurice Dagbert a obtenu lui-même les listes élémentaires (32) par cette méthode simple.
Exemple de calcul complet avec méthode d'élimination des variables :
On fixe par exemple les trois premiers nombres ci à 1, 7 et 15, et leurs correspondants di à 0, 10 et 12.
Cela revient à fixer les trois premières valeurs de δi et de xi.
On se fixe également (premier essai) les valeurs de δ4 = -2 et δ5 = 1.
On cherche alors à calculer les deux derniers nombres c4 et c5, et leurs correspondants d4 et d5
Les calculs donnent : P = 330.25, Q = 83985.06, A = -1, B = 2 P, C = P2 - 2 Q, (B2 - 4 A C) = 447.932
D'où :
x5 = 10.312 ou 23.542
On retient x5 = 23.542, proche du carré d'un demi-entier (vu que δ5/2 = 1/2).
c5 = √x5 + δ5/2 = 24.04
d5 = √x5 - δ5/2 = 23.04
x4 = -(δ5 x5 + P)/δ4 = 21.032
On retient x4 = 21.032, proche du carré d'un entier (vu que δ4/2 = -1).
c4 = √x4 + δ4/2 = 20.03
d4 = √x4 - δ4/2 = 22.03
On injecte les solutions entières c5 = 24, d5 = 23, c4 = 20, d4 = 22, dans les équations exactes (32), qui se trouvent vérifiées dès ce premier essai.
6. Calcul de β1 et β2 à partir de N donné :
La relation (34) est une équation diophantienne pouvant s'écrire plus simplement :
(60) β1 = 9 u - N et β2 = N - 8 u, avec u quelconque
Mais il faut en plus assurer trois contraintes :
1. Les listes partielles de S1 et S2 doivent se raccorder afin de donner l'illusion de deux listes uniques et croissantes de 17 nombres chacune.
2. Ces listes partielles ne doivent pas avoir de doublons entre elles.
Compte tenu des listes translatées (31)(32), ces deux contraintes s'écrivent :
(β2 + Min[L2a*, L2b*]) supérieur et proche de (β1 + Max[L1a*, L1b*])
avec Min[L2a*, L2b*] = -24 et Max[L1a*, L1b*] = 25
Compte tenu des relations (60), cela s'écrit :
(61) u inférieur et proche de u max
avec u max = (2 N - (Max[L1a*, L1b*] - Min[L2a*, L2b*]))/17 = (2 N - 49)/17
Pour N = 2139, u max = 248.8
3. Tous les nombres des listes (La) et (Lb) doivent être supérieur à zéro.
Compte tenu des listes translatées (31)(32), cela s'écrit :
β1 + Min[L2a*, L2b*] > 0
Compte tenu des relations (60), cela s'écrit :
(62) u > u min
avec u min = (N - Min[L2a*, L2b*])/9 = (N + 24)/9
Pour N = 2139, u min = 240.3
Compte tenu des conditions (61)(62), Maurice Dagbert a choisi 247 pour valeur de u, induisant les valeurs 84 et 163 pour β1 et β2.
Il reste à s'assurer que u min < u max pour toute valeur de N.
Compte tenu des conditions (61)(62), cela introduit une nouvelle contrainte :
(63) N > (9 Max[L1a*, L1b*] - 26 Min[L2a*, L2b*] = 849)
Maurice Dagbert a imposé 1000 pour valeur minimale de N afin de satisfaire cette contrainte, qui dispense alors de calculer u min.
7. Absence de doublon dans une liste ou entre listes de 17 nombres :
Cette propriété remarquable résulte de trois constats :
- Par construction, les listes élémentaires C1 et D1 (cf relations (31)) n'ont aucun doublon, ni interne ni entre elles. Il en va donc de même pour les listes translatées L1a* et L1b*, compte tenu de leurs symétries, ainsi que des listes partielles L1a et L1b.
- Par construction également, les listes élémentaires C2 et D2 (cf relations (32)) ont cette même propriété. Il en va donc de même pour les listes translatées L2a* et L2b*, compte tenu de leurs symétries, ainsi que des listes partielles L2a et L2b.
- Par choix précédent (cf relation (61)), les listes partielles L1a et L1b sont disjointes des listes partielles L2a et L2b.
En conséquence, les deux listes de 17 nombres ne peuvent avoir de doublon, en interne ou entre elles, vu qu'elles résultent de la simple concaténation de L1a et L2a pour la première et de L1b et L2b pour la seconde.
8. Construction des listes de 17 nombres :
Les deux listes de 17 nombres fournies par Maurice Dagbert se construisent alors en quatre étapes :
1. Calcul de u selon les relations (61)(62).
2. Calcul de β1 et β2 selon les relations (60).
3. Mémorisation de trois listes d'écarts basées sur les écarts entre nombres consécutifs de chaque liste translatée L1a*, L1b*, L2a*, L2b* (cf relations (31)(32)) :
Liste d'écarts E1 = [ 4, 5, 14, 4, 14, 5, 4]
Liste d'écarts E2 = [ 4, 5, 8, 6, 11, 2, 10, 1 ]
Liste d'écarts E3 = [ 1, 9, 9, 10, 9, 9, 1 ]
4. Construction de deux listes (La) et (Lb) de 17 nombres en fonction de ces listes d'écarts et des translations β1 et β2, selon la répartition suivante :
La = [ L1a, L2a ]
Lb = [ L1b, L2b ]
avec :
L1a = [ (β1 - 25), +E1 ] composé de 8 termes
L2a = [ (β2 - 24), +E2 ] composé de 9 termes
L1b = [ (β1 - 24), +E3 ] composé de 8 termes
L2b = [ (β2 - 23), +E2! ] composé de 9 termes
Le symbole "!" signifie que la liste doit être lue à l'envers.
Nota : Il existe un autre moyen (plus compliqué) pour construire les deux listes de 17 nombres, basé sur la mémorisation des listes élémentaires C1, D1, C2, D2 (cf relations (31)(32)) :
L1a = [ (β1 - C1!)4, (β1 + C1)4 ]
L2a = [ (β2 - C2!)5, (β2 + D2°)4 ]
L1b = [ (β1 - D1!)4, (β1 + D1)4 ]
L2b = [ (β2 - D2°!)4, (β2 + C2)5 ]
Le symbole "!" signifie que la liste doit être lue à l'envers.
Le symbole "°" signifie que le terme fictif 0 de la liste doit être ignoré.
L'indice en partie basse indique, pour rappel, le nombre de termes de la quantité entre parenthèses.
B6.4. Sources :
[ASH] ashmarlow52, Learn This Viral Battery Trick (Youtube, 01:07).
[CAR1] Carrefour francophone, Cours de Magie avec Magislain - Tour 4 : Evasion (Youtube, 03:16).
[CAR2] Carrefour francophone, Cours de magie avec Magislain - Tour 2 : L'élastique à travers les doigts (Youtube, 03:21).
[EIT] Joseph Eitel, The Handcuff Escape Puzzle.
[GAR] Nasr Garouachi, Cordes - Playlist.
[HAF] Nadjib Haffaf, Echapper à la corde facile - DIDACTICIEL (Youtube, 02:45).
[JER] Jérémie-L'école de la magie, 3 TOURS DE MAGIE AVEC 1 ELASTIQUE (Youtube, 08:20).
[MAGE] MagieExpliquée, Apprenez la Téléportation avec un simple Elastique - Secret Révélé (Youtube, 06:43).
[MIR] Minute Facile, Régis le magicien vous explique son incroyable tour de magie avec une corde (Youtube, 03:50).
[PAU] Paulo magie, apprenez un tour impressionnant avec 2 élastiques (Youtube, 05:26).
[PRA] pratiqueTV, Tour de passe passe avec des piles (Youtube, 01:50).
[SHU1] Chen Shuwen, Non-negative Integer Solutions of a1k + a2k + a3k+ a4k = b1k + b2k + b3k + b4k ( k = 2, 4, 6 ).
[SHU2] Chen Shuwen, On the Generalization of the Prouhet-Tarry-Escott Problem.
[TUT] TUTO MAGIE, ARNAQUE OU MAGIE ? COMMENT GAGNER DE L'ARGENT AVEC 3 CARTES EXPLICATION (Youtube, 06:24).
[VAL] TUTUR VAL, 5 TOURS DE MAGIE AVEC DES ELASTIQUES (Youtube, 07:49).
[WIK1] Problème de Prouhet-Tarry-Escott.
Voici une introduction aux jeux de stratégie.
Cette collection regroupe des jeux à un ou plusieurs joueurs, pour lesquels une stratégie est connue, soit gagnante pour l'un des deux joueurs, soit optimale, soit simplement rationnelle.
Sommaire :
B7.1. Jeux avec pions :
Les jeux suivants avec pions ont tous une stratégie gagnante pour l'un des deux joueurs.
B7.1.1. Le jeu des 17 allumettes :
Le jeu des 17 allumettes est un jeu de stratégie à deux joueurs, dans lequel il existe une stratégie gagnante selon la variante choisie.
Règles du jeu :
Deux joueurs se trouvent face à un tas de 17 allumettes.
Les joueurs jouent à tour de rôle et chacun retire 1, 2 ou 3 allumettes.
Deux variantes existent alors :
V1. Celui qui vide le tas gagne la partie.
V2. Celui qui vide le tas perd la partie.
Stratégie gagnante :
V1 : le premier joueur gagne en ramenant toujours le jeu à un multiple de 4 allumettes (c'est-à-dire : 16, 12, 8, 4, 0).
V2 : le second joueur gagne en ramenant toujours le jeu à un multiple de 4 + 1 allumettes (c'est-à-dire : 13, 9, 5, 1).
Explication :
On peut représenter le jeu par un graphe orienté (appelé graphe des options), où chaque sommet correspond à une position n du jeu (nombre d'allumettes restantes) et chaque arête correspond à un coup possible (passer de la position
n
à la position
n - 1, n - 2 ou n - 3). Voir Figure ci-dessus.
On distingue alors deux types de positions :
- une position gagnante (G en blanc) lorsqu'il existe au moins un coup menant à une position perdante (P en jaune).
- une position perdante (P) lorsque tous les coups possibles mènent à des positions gagnantes (G).
Variante V1 :
La position 0 est perdante pour le joueur dont c'est le tour (il ne peut pas jouer et a perdu).
En remontant le graphe, on constate que :
- 1, 2 et 3 sont gagnantes,
- 4 est perdante,
-
puis, par récurrence, toutes les positions multiples de 4 sont perdantes.
Ces positions perdantes correspondent exactement aux positions dont le nombre de Grundy (noté 'mex') est nul (car il s'agit d'un jeu impartial), ce qui explique pourquoi le joueur qui sait les identifier peut toujours forcer la victoire.
Variante V2 :
La position 0 est gagnante pour le joueur dont c'est le tour (il gagne sans jouer puisque l'adversaire a pris la dernière allumette).
En remontant le graphe, on constate que :
- 1 est perdante,
- 2, 3 et 4 sont gagnantes,
-
puis, par récurrence, toutes les positions de la forme 4 k + 1 sont perdantes (avec k entier non négatif).
Là encore, ces positions perdantes sont exactement celles dont le nombre de Grundy est nul, expliquant la périodicité modulo 4.
Nombre de Grundy :
Dans un jeu impartial (comme celui des 17 allumettes), le nombre de Grundy g(n) d'une position n quelconque est défini comme le mex (minimum exclu) des nombres de Grundy de ses positions accessibles en un coup, où mex désigne le plus petit entier naturel absent de l'ensemble.
Toute position sans coup possible a par ailleurs un nombre de Grundy égal à 0.
Appliqué au jeu des 17 allumettes, cela conduit à la relation de récurrence suivante :
g(n) = mex{g(n - 1), g(n - 2), g(n - 3)} pour n ≥ 1
Variante V1 :
g(0) = 0 puisque, depuis la position 0, aucun coup n'est possible, d'où le résultat : g(n) = n mod 4
Variante V2 :
g(1) = 0, d'où le résultat : g(n) = (n - 1) mod 4
Interprétation : Les positions dont le nombre de Grundy est nul sont exactement les positions perdantes. La stratégie gagnante consiste donc à jouer de façon à ramener systématiquement l'adversaire sur une position de Grundy nul.
B7.1.2. Le jeu des tas :
Le jeu des tas, ou jeu de Nim ou jeu de Marienbad, est un jeu de stratégie gagnante à deux joueurs fondé sur des principes mathématiques simples et fascinants.
Règles du jeu :
Deux joueurs se trouvent face à plusieurs tas d'objets (pierres, cartes, allumettes, coquilles Saint-Jacques), le nombre de tas et le nombre d'objets par tas étant arbitraires.
Les joueurs jouent à tour de rôle et chacun retire autant d'objets qu'il veut (mais au moins un) d'un seul tas.
Celui qui vide le dernier tas remporte la partie.
Stratégie gagnante :
La méthode gagnante repose sur une addition particulière appelée "Nim_addition". On calcule la somme XOR des tailles des tas écrites en numération binaire (c'est-à-dire le "ou exclusif" bit à bit, dont le bit du résultat vaut 1 si et seulement si les bits sont différents).
Si cette Nim_addition est nulle, la position est perdante (on parle de position "paire"). Dans le cas contraire, la position est gagnante (position "impaire") et il existe toujours au moins une action permettant de ramener la Nim_addition à zéro.
Exemple (voir Figure ci-dessus) : supposons trois tas de taille 3 (011 en binaire), 4 (100 en binaire) et 5 (101 en binaire). La Nim_addition (notée "⊕") vaut : 3 ⊕ 4 ⊕ 5 = 2 (10 en binaire), ce qui n'est pas nul. Le premier joueur peut donc gagner en ajustant la taille de l'un des tas.
Une manière plus visuelle de procéder est la suivante [DEL1]. On décompose chaque taille en paquets pi ayant chacun un nombre i d'objets, où i est une puissance de 2, ce qui revient à écrire ces tailles en numération binaire.
Pour chaque puissance de 2, on compte le nombre total de paquets correspondants. Une position est perdante si ce nombre est pair pour toutes les puissances de 2.
Dans l'exemple précédent, on a : 3 = p2 + p1 ; 4 = p4 ; 5 = p4 + p1. Ici, le paquet p2 apparaît une seule fois. Pour rétablir une position paire, il faut donc enlever ce paquet, ce qui revient à réduire le tas de taille 3 à 1.
Explication :
Soit n tas avec ti la taille du tas i. La Nim_addition vaut : S = t1 ⊕ ... ⊕ ti ⊕ ... ⊕ tn
Un coup légal consiste à choisir un tas m et à modifier sa taille tm par un entier strictement plus petit t'm, les autres tas restant inchangés.
La Nim_addition initiale S s'écrit alors : S = t1 ⊕ ... ⊕ tm ⊕ ... ⊕ tn
Après le coup joué, elle devient : S' = t1 ⊕ ... ⊕ t'm ⊕ ... ⊕ tn
Compte tenu de l'identité : tm ⊕ tm = 0, de la commutativité et de l'associativité de l'opérateur XOR, cela s'écrit aussi :
(*) S' = S ⊕ (tm ⊕ t'm)
1. Cas S = 0 : Une position paire mène toujours à une position impaire.
Compte tenu de la relation (*), si S = 0, alors on a : S' = tm ⊕ t'm
Comme tm ≠ t'm, on a nécessairement : tm ⊕ t'm ≠ 0, donc S' ≠ 0.
La nouvelle position est donc impaire.
2. Cas S ≠ 0 : A partir d'une position impaire, il existe au moins une action menant à une position paire.
Si S ≠ 0, soit r max le rang du bit de poids fort non nul de S. Dans l'exemple précédent (S = 10 en binaire), r max correspond au second rang à partir de la droite.
Il existe alors au moins un tas m dont la taille tm possède un bit égal à 1 au rang r max.
On définit alors une nouvelle taille t'm = tm ⊕ S
Au rang r max, on a un 1 dans tm et un 1 dans S, donc le bit de rang r max devient 0 dans t'm. Par ailleurs, aucun bit de rang supérieur n'est modifié. On a donc : t'm < tm et cette action permet de jouer un coup légal en réduisant la taille du tas tm.
La relation (*) s'écrit alors :
S' = S ⊕ (tm ⊕ (tm ⊕ S)) = (S ⊕ S) ⊕ (tm ⊕ tm) = 0
La nouvelle position est donc paire.
B7.1.3. Le Nim de Moore :

Une généralisation du jeu des tas, appelée Nim de Moore, est définie comme suit [DEL1] :
Règles du jeu :
A chaque tour, le joueur choisit entre 1 et k tas distincts (k fixé, exemple : k = 2) et retire au moins un objet de chacun des tas choisis.
Stratégie gagnante :
La méthode consiste à écrire la taille de chaque tas en binaire (comme pour le jeu des tas), puis à calculer une "Moore_addition" qui est le vecteur obtenu en additionnant les bits de chaque tas colonne par colonne modulo (k + 1).
La position est paire (et perdante) si toutes les colonnes donnent un reste nul, et impaire (et gagnante) dans le cas contraire.
Exemple (voir Figure ci-dessus) : supposons k fixé = 2 et trois tas de taille 3 (11 en binaire), 4 (100 en binaire) et 5 (101 en binaire). La Moore_addition (notée "⊕") vaut : 3 ⊕ 4 ⊕ 5 = vecteur 212, ce qui n'est pas nul. Le premier joueur peut donc gagner en ajustant la taille de un ou deux tas, par exemple en retirant 1 objet du tas de 4 et 2 objets du tas de 5. La position devient alors : 3 ⊕ 3 ⊕ 3 = 0 qui devient paire pour l'autre joueur.
Explication :
Soit n tas avec ti la taille du tas i, et un entier k fixé entre 2 et n. La Moore_addition vaut : S = {c1, c2, ..., cr, ...} avec cr = (nombre de tas dont le bit au rang r vaut 1) mod (k + 1)
1. Cas S = 0 : Une position paire mène toujours à une position impaire.
Si S = 0, alors pour tout rang r, le nombre cr de bits à 1 est divisible par k + 1, ce qui s'écrit : cr = 0 mod (k + 1).
Soit r max le plus grand rang effectivement modifié parmi les tas choisis par le joueur. Dans cette colonne, seuls les tas modifiés peuvent changer des bits. Comme le joueur ne peut modifier au plus que k tas, cr max varie d'un entier de valeur absolue au plus égale à k.
Aucune variation non nulle de valeur absolue au plus égale à k n'étant divisible par (k + 1), la divisibilité par (k + 1) dans cette colonne est rompue.
La nouvelle position est donc impaire.
2. Cas S ≠ 0 : A partir d'une position impaire, il existe au moins une action menant à une position paire.
Si S ≠ 0, soit r max le rang du bit de poids fort non nul de S.
Soit T l'ensemble des tas k dont la taille tk possède un bit égal à 1 au rang r max.
Parmi ces tas, on peut alors choisir un sous-ensemble T' de 1 à k tas tel que, si l'on bascule le bit de rang r max dans chacun des tas de T' de 1 à 0 (en diminuant convenablement ces tas), le nouveau nombre de 1 dans cette colonne devienne multiple de (k + 1).
On procède alors par récurrence descendante sur les rangs : pour chaque rang r < r max, on ajuste éventuellement les mêmes tas (toujours en les diminuant) de sorte que la colonne r devienne elle aussi multiple de (k + 1), sans jamais modifier les bits de rang strictement supérieur déjà fixés.
A chaque étape, on agit sur au plus k tas, de sorte que cette correction locale est toujours possible, exactement comme on "corrige" les colonnes une à une dans le jeu des tas (k = 1) avec l'opérateur XOR.
Au terme de ce processus, toutes les colonnes ont un nombre de bits à 1 divisible par (k + 1).
La nouvelle position est donc paire.
Sur l'exemple des trois tas précédents (avec k fixé à 2), le procédé de correction colonne par colonne est le suivant :
- Les trois tas ti s'écrivent en binaire comme suit :
t1 = 3 = 011
t2 = 4 = 100
t3 = 5 = 101
- La Moore-addition donne S = 212, qui n'est pas nulle (position impaire).
- La colonne r max vaut 2 avec T = {t2, t3}
- On peut agir sur au plus k = 2 tas. Ici, ces 2 tas suffisent avec T' = T
- Pour rendre la colonne de rang 2 multiple de 3, il faut enlever les 1 de ces deux tas.
- Une façon de faire est de viser la position {ti} = {3, 3, 3}, seule solution possible avec k = 2
- On laisse le tas 1 inchangé, on diminue le tas 2 de 1 objet et le tas 3 de 2 objets.
Nota : Pour k = 3, il existe plusieurs solutions aboutissant respectivement aux positions {ti} = {3, 3, 3} ou {2, 2, 2} ou {1, 1, 1}.
B7.1.4. Le jeu des chameaux :
Le jeu des chameaux, ou jeu des pièces de dix francs, ou jeu du "pousse-coque", est une variante du jeu des tas, définie comme suit :
Règles du jeu :
Le jeu se joue sur une ligne de cases comportant une case initiale et plusieurs pièces, une par case, placées initialement à des distances arbitraires entre pièces (voir Figure ci-dessus).
Le nombre de pièces doit être pair. Dans le cas impair, il faut ajouter une pièce fictive, placée juste avant la case initiale.
Les joueurs jouent à tour de rôle et chacun déplace une seule pièce vers la case initiale, d'une ou plusieurs cases, sans sauter une pièce déjà en place.
Cette façon de se déplacer est analogue à une caravane de chameaux en file indienne dans le désert, chaque animal suivant l'autre sans pouvoir le dépasser.
La partie s'arrête lorsque tous les pièces sont bloquées.
Le joueur qui joue le dernier coup gagne la partie.
Stratégie gagnante :
La stratégie gagnante consiste à jouer comme au jeu des tas en maintenant une position à Nim_addition nulle, et, lorsqu'un coup modifie cette lecture en augmentant un tas, à effectuer immédiatement un coup de restauration afin de revenir à une position Nim équivalente.
La méthode est la suivante [TRI1] :
1. La position initiale est fixée. Voir en exemple la Figure ci-dessus "Position initiale" = 0111000001001000011000001, la case initiale étant à gauche, avec 0 désignant une case libre et 1 une case occupée par une pièce.
2. En partant de la pièce la plus éloignée de la case initiale, former des paires disjointes de pièces successives depuis la case la plus éloignée de la case initiale, chaque pièce n'appartenant qu'à une seule paire, puis compter le nombre de cases libres à l'intérieur de chaque paire.
Ce comptage revient à définir un ensemble de tas d'objets. Voir Figure ci-dessus "Position initiale" montrant la configuration (0, 5, 4, 5) de ces tas.
3. Ensuite, déplacer une pièce sur la ligne de cases revient à retirer autant d'objets que l'on veut d'un tas parmi plusieurs, le vainqueur étant celui qui vide le dernier tas.
Cette règle de jeu est exactement celle du jeu des tas et l'on joue pour atteindre une position paire gagnante. Voir Figure ci-dessus "Joueur A - Coup n°1" = 0111010000001000011000001, montrant le déplacement permettant d'aboutir à la configuration gagnante (0, 1, 4, 5) correspondant à la Nim_addition 0 ⊕ 1 ⊕ 4 ⊕ (4 ⊕ 1) = 0.
4. Mais, contrairement au jeu des tas, un coup peut augmenter la taille d'un tas.
Voir Figure ci-dessus "Joueur B - Coup n°1" = 0111011000000000011000001, montrant un tel déplacement aboutissant à la configuration (0, 1, 10, 5).
5. Pour se ramener à une position "Nim équivalente", il faut alors annuler tout coup de l'adversaire qui augmenterait la taille de l'un des tas. Pour cela, il faut ramener à sa valeur initiale la taille du tas.
Voir Figure ci-dessus "Joueur A - Coup n°2" = 0111011000010000001000001, montrant le déplacement permettant de revenir à la configuration gagnante précédente (0, 1, 4, 5).
B7.2. Jeux avec damier :
Les jeux suivants se jouent sur un échiquier classique 8 x 8 ou un damier 10 x 10 de type dames internationales.
B7.2.1. Le jeu de Northcott :
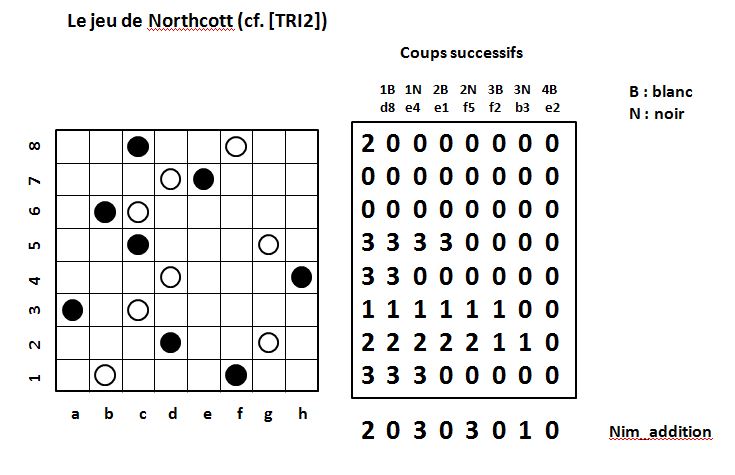
Le jeu de Northcott, inventé par le mathématicien américain D.G. Northcott, est une variante du jeu des tas et du jeu des chameaux, définie comme suit :
Les règles du jeu sont les suivantes :
Configuration initiale :
Le jeu se joue sur un échiquier classique 8 x 8, chaque joueur disposant de 8 pions, les blancs pour l'un, les noirs pour l'autre (voir Figure ci-dessus).
Les joueurs posent leurs pions sur les cases de l'échiquier, un de chaque couleur par rangée de l'échiquier, sans qu'ils occupent la même case.
On obtient ainsi sur chacune des 8 rangées, un pion noir et un pion blanc.
Objectif :
Les joueurs jouent à tour de rôle.
Chaque joueur choisit un de ses pions et le déplace horizontalement sur sa rangée, d'un nombre quelconque de cases, vers la droite ou vers la gauche, sans sauter le pion adverse.
Le joueur qui joue le dernier coup gagne la partie.
Dans la version originale, le jeu se termine dès que les pions sont tous adjacents (même au centre des rangées).
La variante bord-bloqué prolonge la partie jusqu'au blocage complet des pions aux bords de l'échiquier. Cette règle rend le jeu plus symétrique et visuellement concluant.
Stratégie gagnante :
La méthode est exactement celle du jeu des tas. Chaque rangée correspond à un tas dont la taille est le nombre de cases libres entre les deux pions (blanc et noir) de cette rangée.
La stratégie optimale est donc le calcul de la Nim_addition de ces 8 valeurs.
Cependant, comme au jeu des chameaux, le joueur peut augmenter la taille d'un tas (en reculant son pion), ce qui ne change rien à la stratégie, la situation pouvant être rétablie au coup suivant.
Exemple (voir Figure ci-dessus, cf [TRI2]) :
1. La configuration initiale des tas est donnée par la première colonne du tableau de la Figure. Elle vaut (2, 0, 0, 3, 3, 1, 2, 3) dont la Nim_addition vaut 1 ⊕ 3 = 2 ≠ 0.
2. Supposons que les pions blancs appartiennent au joueur gagnant. Pour laisser une position paire à son adversaire, ce joueur devra ôter 2 à l'une des rangées, par exemple en déplaçant son pion blanc en position d8, laissant une configuration (0, 0, 0, 3, 3, 1, 2, 3) dont la Nim-addition vaut 0 (voir Figure ci-dessus).
3. Les coups suivants pour les deux joueurs sont donnés dans le tableau de la Figure.
4. Dans le cas où les pions blancs et noirs sont tous l'un contre l'autre, mais sans être tous bloqués contre les bords de l'échiquier, le joueur contraint de jouer (joueur des noirs) ne peut que reculer un des pions en augmentant le nombre de cases libres entre pions, que l'autre joueur (joueur des blancs) ramène immédiatement à 0.
5. La partie se termine donc au profit du joueur initialement gagnant (joueur des blancs), que ce soit dans la version originale du jeu ou la variante bord-bloqué.
B7.2.2. Le jeu du loup et des agneaux :

Le jeu du loup et des agneaux est un jeu de stratégie gagnante à deux joueurs.
Les règles du jeu sont les suivantes :
Configuration initiale :
Le jeu du loup et des agneaux se joue sur un damier de type dames internationales 10 x 10, orienté avec une case blanche en bas à droite, et en utilisant uniquement les cases blanches.
Au début de la partie, le loup (pion noir) est placé sur l'une des cases blanches d'un bord du damier, au choix du joueur qui le dirige. Les 5 agneaux (pions blancs) sont placés en ligne sur les 5 cases blanches du bord opposé.
Objectif :
Les joueurs jouent à tour de rôle.
Le loup commence la partie. Son objectif est de franchir la ligne formée par les agneaux et d'atteindre le bord opposé du damier occupé initialement par ceux-ci.
Les agneaux gagnent s'ils parviennent à bloquer totalement le loup.
Règles de déplacement :
Le loup se déplace d'une seule case en diagonale, vers l'avant ou vers l'arrière.
Les agneaux se déplacent également d'une seule case en diagonale, mais uniquement en avant.
Règles de capture :
Il n'y a ni capture ni saut.
Stratégie gagnante :
La stratégie est gagnante pour les agneaux en 25 coups environ s'ils respectent sans erreur les règles suivantes [PER][CHA] :
1. Avancer sans poursuivre : Les agneaux ne doivent jamais chercher à encercler le loup ni à progresser vers sa position. L'objectif est de réduire progressivement l'espace de mouvement du loup, jamais de l'attaquer.
2. Avancer en ligne compacte
: Les agneaux doivent rester alignés sur une même rangée ou sur deux rangées adjacentes, sans avancées isolées, afin de ne jamais créer de trou exploitable.
3. Bloquer les deux coups possibles du loup : Les agneaux doivent occuper en priorité les deux cases situées en diagonale juste devant le loup.
4. Ne jouer que des coups utiles : Les agneaux ne doivent effectuer que des déplacements qui contribuent directement au respect des trois règles précédentes.
5. Bloquage final : lorsque le loup est coincé contre un bord ou dans un coin du damier, les agneaux peuvent rompre la ligne compacte afin d'occuper toutes les cases diagonales adjacentes accessibles.
B7.2.3. Le jeu de dames :

Les règles du jeu sont les suivantes [PER][CHA] :
Configuration initiale :
Le jeu de dames internationales se joue sur un damier 10 x 10, orienté avec une case blanche en bas à droite, et en utilisant uniquement les cases noires.
Au début de la partie, 20 pions blancs et 20 pions noirs sont placés sur les quatre premières rangées de chaque côté des joueurs.
Objectif :
Les joueurs jouent à tour de rôle.
Les Blancs jouent toujours en premier.
Un joueur gagne si l'adversaire n'a plus de pièces ou ne peut plus bouger.
La partie est déclarée nulle si :
- Aucun joueur ne peut progresser vers une capture (par exemple, lorsque le jeu ne comporte que des dames mobiles, sans possibilité de capture),
- La même position se répète trois fois avec le même joueur au trait et les mêmes possibilités de mouvement,
- 25 coups consécutifs sont joués sans prise ni promotion de dame.
Règles de déplacement :
- Les pions se déplacent d'une case en diagonale vers l'avant si la case est libre.
- Une dame se déplace en diagonale sur plusieurs cases, avant ou arrière, tant que la case est libre.
Règles de capture :
- Une pièce (pion ou dame) peut sauter, en avant ou en arrière, une ou plusieurs pièces adverses en un seul tour, sans pouvoir toutefois sauter plusieurs fois la même pièce.
- Chaque pièce adverse sautée est capturée et enlevée du jeu à la fin de la séquence complète de captures.
- Si une pièce peut capturer, elle doit le faire obligatoirement. Si plusieurs séquences de capture sont possibles (rafle), le joueur doit choisir obligatoirement celle qui capture le plus de pièces.
Règles spéciales :
- Promotion : Un pion devient dame lorsqu'il atteint la dernière rangée adverse, symbolisé par l'empilement d'un deuxième pion.
- Toucher-jouer : Une pièce touchée doit être jouée, sauf pour annoncer "j'adoube" (ajuster sa position) avant de toucher la pièce.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au jeu de dames, connue à ce jour. La stratégie optimale consiste à minimiser les erreurs grossières en suivant les règles suivantes [PER][CHA] :
1. Avancer en bloc : Les pions en tandem ou groupes de 2 ou 3 se protègent mutuellement et compliquent les captures adverses.
2. Protéger par formation pyramidale : Quand on avance une pièce, s'assurer que deux autres pièces en diagonale arrière la protègent.
3. Jouer d'abord au centre : Les ailes sont difficiles à défendre et faciles à bloquer.
4. Simplifier le jeu : Provoquer des échanges simples (1 pour 1) dès que possible, à condition de garder une position compacte. Moins de pièces signifie moins de pièges possibles.
5. Détecter les diagonales ouvertes : Lorsqu'il existe de longues diagonales ouvertes, vérifier que l'adversaire ne peut pas les exploiter pour placer une dame ou déclencher une rafle, tout en les exploitant offensivement soi-même.
6. Anticiper les rafles : Vérifier avant de jouer que le coup n'implique pas une rafle adverse.
7. Sécuriser toute promotion de dame : Avant de tenter une promotion, vérifier que la case d'arrivée ne permet pas une capture immédiate.
8. Couronner tôt : Viser à promouvoir 1 ou 2 pions rapidement en dames pour prendre le contrôle du jeu.
B7.2.4. Les échecs :
Les règles du jeu sont les suivantes [PER][CHA] :
Configuration initiale :
Les échecs se jouent sur un damier 8 x 8, orienté avec une case blanche en bas à droite.
Au début de la partie, 16 pièces blanches et 16 pièces noires sont placées comme suit :
- sur la première rangée : en partant de chaque extrémité, une tour, un cavalier, un fou. Les deux cases centrales sont occupées par le roi et la dame, la dame étant placée sur la case de sa couleur.
- sur la seconde rangée : les 8 pions.
Objectif :
Les joueurs jouent à tour de rôle.
Les Blancs jouent toujours en premier.
Un joueur gagne la partie s'il met le roi adverse en échec et mat, ou si l'adversaire dépasse la limite de temps alors que le joueur a un matériel suffisant pour mater l'adversaire.
Règles de déplacement :
- Roi : Une seule case dans toute direction (horizontale, verticale, diagonale). Il ne peut pas se déplacer sur une case le mettant en échec.
- Dame : Toute distance dans toute direction, si chemin libre.
- Fou : Toute distance diagonale, si chemin libre.
- Cavalier : déplacement en L (2 cases dans une direction et 1 autre perpendiculairement). Il est la seule pièce à sauter par-dessus les autres.
- Tour : Toute distance horizontale ou verticale, si chemin libre.
- Pion : Avance d'une seule case vers l'avant, dans la colonne où il se trouve (et 2 cases possibles depuis sa position initiale, si chemin libre). Il ne recule jamais.
Règles de capture :
- Toutes les pièces, sauf le pion, capturent selon leur déplacement normal en occupant la case adverse.
- Le pion capture uniquement d'une case en diagonale avant (droite ou gauche), jamais en ligne droite.
- Prise en passant : Un pion avançant de 2 cases depuis sa position initiale et se plaçant à côté d'un pion adverse, peut être capturé par ce dernier au coup immédiatement suivant, comme s'il n'avait avancé que d'une case. La capture s'effectue en diagonale sur la case que le pion capturé aurait occupée après un déplacement d'une seule case.
- La pièce qui capture prend la place de la pièce capturée, laquelle est retirée du jeu.
Règles spéciales :
- Promotion : Un pion atteignant la dernière rangée se transforme en dame, tour, fou ou cavalier (avec choix immédiat).
- Roque : Le roi se déplace de deux cases dans sa rangée d'origine vers la tour adjacente, laquelle saute ensuite par-dessus le roi pour se placer à côté de lui. Deux roques différents sont possibles mais un seul par joueur et par partie : grand roque côté dame et petit roque côté roi. Les conditions de roque sont les suivantes :
1. Le roi et la tour concernés n'ont pas bougé auparavant.
2. Le chemin est libre entre eux (aucune pièce intermédiaire).
3. Le roi n'est pas en échec au moment du roque.
4. Le roi ne traverse pas de case menacée.
5. Les cases finales du roi et de la tour ne sont pas menacées.
- Toucher-jouer : Une pièce touchée doit être jouée (déplacée si pièce alliée, capturée si pièce adverse), sauf pour annoncer "j'adoube" (ajuster sa position) avant de toucher la pièce.
Règles de fin de partie :
- Echec au roi : Le roi est menacé. Trois parades sont possibles (acronyme PIF) : Prendre l'attaquant, Interposer une pièce entre roi et attaquant, Fuir la menace.
- Echec et mat : Le roi est en échec sans parade possible.
- Partie nulle : les cas possibles sont les suivants :
1. Pat : Aucun coup légal n'est possible, avec roi non en échec.
2. Partie nulle par accord : Les deux joueurs acceptent d'arrêter.
3. Triple répétition : La même position exacte est répétée trois fois au cours de la partie, avec le même joueur au trait.
4. Règle des 50 coups : 50 coups consécutifs sont joués par chaque joueur sans capture ni mouvement de pion.
5. Mat impossible par insuffisance de matériel : Le mat est impossible dans toute position possible (exemples : roi seul contre roi ; roi + cavalier contre roi ; roi + fou contre roi ; etc.).
6. Position morte (forteresse) : Le mat est impossible depuis la position actuelle (exemple : roi blanc dans un coin avec trois pions blancs bloquant l'accès au roi, contre dame noire).
7. Temps écoulé sans mat possible (article 6.9 de la FIDE pour le principe général et 6.12.1 pour l'exception de nullité) : La partie est nulle si un joueur dépasse la limite de temps et que l'autre joueur a un matériel insuffisant pour mater son adversaire.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante aux échecs, connue à ce jour. La stratégie optimale consiste à minimiser les erreurs grossières en suivant les règles suivantes [PER][CHA] :
1. Principe fondamental : La plupart des parties se gagnent par les erreurs de l'adversaire plutôt que par des coups parfaits.
2. Développer rapidement ses pièces :
- Sortir les cavaliers et les fous dès l'ouverture vers des cases actives.
- Eviter de déplacer plusieurs fois la même pièce sans nécessité.
3. Assurer la sécurité du roi :
- Roquer tôt, sauf raison tactique contraire.
- Eviter d'exposer le roi au centre en début de partie.
4. Occuper ou contrôler le centre :
- Exercer une influence sur les cases centrales (d4, d5, e4, e5) par pions et pièces, soit par occupation directe, soit par contrôle à distance.
- N'attaquer sur les ailes qu'après stabilisation du centre.
- Eviter de sortir la reine trop tôt.
5. Sécuriser les pièces :
- Placer les pièces sur des cases où elles ont de nombreuses possibilités d'action.
- Coordonner les pièces afin qu'elles se soutiennent mutuellement.
6. Structurer les pions :
- Chaque mouvement de pion modifie durablement la position et doit être justifié par un plan.
- Eviter les pions doublés (sur une même colonne), isolés (sans pions alliés sur les colonnes adjacentes) ou arriérés (en retard sur sa colonne).
7. Echanger avec tactique :
- Favoriser les échanges de pièces quand ils améliorent sa position.
- Simplifier la position lorsqu'on dispose d'un avantage matériel ou positionnel.
8. Traquer les menaces :
- Vérifier les menaces à chaque coup.
- Ne pas laisser de pièces en prise.
9. Exploiter les faiblesses adverses :
- Pions doublés, isolés ou arriérés
- Cases faibles (celles que les pions adverses ne contrôlent plus) : occuper la case avec un cavalier (meilleur choix).
- Pièces bloquées ou mal placées : forcer les échanges défavorables à l'adversaire.
- Mauvais fou (fou sur cases de la même couleur que les pions) : ne jamais l'échanger contre une de ses pièces actives, sauf exception rare.
10. Anticiper la finale :
- Activer votre roi : il devient une pièce offensive une fois en sécurité.
- La structure de pions prend une importance accrue.
11. Gérer son temps :
- Eviter de consommer trop de temps en début de partie.
B7.3. Jeux avec cartes :
Les jeux de cartes suivants illustrent différentes façons de jouer avec le hasard, où la réflexion, la patience et parfois la ruse influencent le résultat.
B7.3.1. La réussite du prisonnier :

La réussite du prisonnier, ou jeu de l'Accordéon, ou "La poussette", se joue seul et nécessite un jeu de 32 ou 52 cartes.
Règles du jeu :
L'histoire raconte qu'elle faisait passer le temps aux prisonniers dans leur cellule.
Les règles du jeu sont les suivantes [PER][CHA] (voir également la vidéo [JEU]) :
Le joueur tient le paquet de cartes face cachée et les tire une à une, les étalant en ligne unique face visible sur le sol ou sur une table.
Dès qu'une carte se trouve encadrée par deux cartes voisines de même valeur (toutes figures ou nombres, comme deux 7 ou deux dames) ou de même couleur exacte (pique, coeur, carreau ou trèfle), il la place sur la carte précédente et resserre l'espace vacant.
Chaque recul peut créer un nouvel encadrement local et potentiellement un second juste en amont. La priorité absolue va alors à l'encadrement le plus en amont non encore traité, de manière récursive jusqu'à ce qu'aucun encadrement ne subsiste dans la ligne complète de cartes étalées.
Cette règle hiérarchique assure un traitement optimal des encadrements, évitant les omissions et accélérant la convergence vers deux tas finaux.
Exemple (voir Figure ci-dessus) : les cartes tirées successivement sont les suivantes :
As Coeur, Valet Trèfle, 8 Pique, 5 Coeur, Valet Pique.
Les opérations sont alors les suivantes :
As coeur, Valet Trèfle, 8 Pique, 5 coeur, Valet Pique, 5 coeur sur 8 Pique, Valet Trèfle sur As Coeur, 5 Coeur sur Valet Trèfle.
La partie se termine ici au premier étalement avec deux tas uniques (5 Coeur, Valet Pique).
Quand toutes les cartes du jeu ont été tirées avec traitement de tous les encadrements en cours, le joueur ramasse les cartes en les empilant de l'aval vers l'amont, retourne le jeu face cachée et recommence un nouvel étalage.
Le but du jeu est de réduire l'étalement à deux tas uniques, ce qui est généralement faisable et très long.
Toutefois, il existe une probabilité non nulle d'échec (inférieure à 5 % selon les études empiriques). Par exemple, lors d'un étalage des cartes, si aucune ne se trouve en encadrement, alors les étalages suivants reproduiront exactement la configuration initiale ou son inverse selon la méthode de ramassage des cartes.
B7.3.2. La bataille :

La bataille un jeu simple pour deux joueurs qui nécessite un jeu de 32 ou 52 cartes.
En version moderne, les règles sont les suivantes [WIK1] :
Objectif :
On distribue une à une toutes les cartes du jeu entre les joueurs, qui les rassemblent face cachée en un seul paquet.
Chaque joueur tire ensuite la carte du dessus de son paquet et la pose face visible sur la table.
L'as est la plus forte carte, puis viennent le roi, la dame, le valet, le 10, puis les autres valeurs par ordre décroissant.
Le joueur qui a la carte la plus forte en valeur remporte le pli. Il ramasse toutes les cartes posées et les place sous son paquet.
En cas d'égalité - appelée "bataille" - les joueurs tirent chacun une nouvelle carte et la posent, face cachée, sur la carte déjà posée, puis une seconde carte qu'ils posent face visible sur les deux autres posées. C'est cette dernière carte qui départage les joueurs. Si une nouvelle égalité survient, cette procédure est répétée autant de fois que nécessaire.
Le gagnant de la partie est celui qui remporte toutes les cartes du paquet de son adversaire.
La partie est déclarée nulle - quand bien même l'un des deux adversaires aurait une supériorité manifeste - si la dernière carte posée par un joueur est une carte face cachée ou si elle est de même valeur que la carte de l'adversaire. Dans ces deux cas, la bataille ne peut pas avoir lieu.
Variante :
Il existe une variante où chaque joueur reçoit au départ un jeu complet de 32 cartes, mélangé indépendamment.
On joue ensuite exactement selon les règles classiques.
Cette variante a l'avantage de supprimer l'injustice initiale liée au partage des cartes d'un seul jeu complet.
En revanche, la durée de la partie se trouve doublée.
Stratégie gagnante :
La bataille est un jeu de pur hasard, donc sans stratégie gagnante.
La partie dure environ (en médiane) 30 minutes avec 350 plis pour un jeu de 52 cartes, et 20 minutes avec 250 plis pour un jeu de 32 cartes - idéal pour une partie familiale rapide.
B7.3.3. La crapette :
La crapette est un jeu de cartes de la famille des réussite pour deux joueurs, qui nécessite deux jeux de 52 cartes (sans joker).
Le mot "crapette" pourrait signifier "petit crapaud bombé", par analogie avec le tas de 13 cartes cachées, bombé comme un crapaud accroupi, avec son oeil en dernière carte visible.
Les règles du jeu en version souple (dite familiale) sont les suivantes [PER][CHA] :
Configuration initiale :
Chaque joueur dispose de son propre jeu qu'il bat et commence à étaler sur la table selon la configuration suivante (voir Figure ci-dessus) :
- Crapette : Chacun tire 13 cartes qu'il met en tas faces cachées devant lui à sa droite.
- Suites latérales (ou piles de travail) : Chacun tire 4 autres cartes qu'il dispose à sa droite, faces visibles, en une colonne personnelle verticale. Ces cartes constituent le début de 8 piles (4 personnelles et 4 adverses).
- Suites centrales : 8 emplacements centraux communs aux deux joueurs sont laissés vides. Ils recevront ultérieurement 8 piles de cartes, faces visibles, disposées en 2 colonnes verticales de 4 couleurs chacune.
- Talon : Les 35 cartes restantes sont mises en tas faces cachées, à gauche de la crapette.
- Ecart (ou défausse) : Cet autre tas, vide initialement, est situé entre talon et crapette. Il reçoit, face visible, la carte du talon lorsqu'elle ne peut pas être placée sur le jeu.
Départage initial :
- Chaque joueur retourne ensuite la carte de dessus de sa crapette. La plus forte carte en valeur (selon l'ordre décroissant : As, Roi, Dame, ..., 2) détermine qui va commencer la partie.
- En cas d'égalité, les joueurs comparent les 4 cartes des suites latérales personnelles, position par position, du haut vers le bas.
Objectif : Chaque joueur doit se défaire de toutes ses cartes en empilant les cartes, faces visibles :
- soit dans les suites centrales constituées de 8 piles croissantes depuis l'As jusqu'au Roi, et de même couleur (Pique, Coeur, Carreau, Trèfle). Cet empilage est définitif, sans possibilité de retirer une carte d'une pile.
- soit dans les suites latérales constituées de 8 piles décroissantes depuis le Roi jusque l'As, en alternant les couleurs opposées (noir/rouge). Cet empilage est provisoire, les cartes étant destinées à être transferrées dans les suites centrales.
- soit sur les tas de son adversaire (crapette ou écart) à condition que la carte soit de même couleur et de rang immédiatement supérieur ou inférieur (par exemple, un 10 de Pique sur un 9 ou Valet de Pique).
Les joueurs jouent à tour de rôle, un joueur jouant autant de fois qu'il peut jouer.
Le gagnant est le premier qui arrive à déposer toutes ses cartes sur la table.
En cas de blocage, le joueur qui a le moins de cartes au total (crapette + écart + talon) a également gagné.
Sources de pioche : On ne pioche jamais chez l'adversaire, que ce soit dans ses tas ou dans ses suites latérales personnelles.
Les sources de pioche sont les suivantes (avec ordre à respecter) :
- Ordre strict : 1. Crapette personnelle, 2. Talon personnel, 3. Ecart personnel.
- Complément de pioche à tout moment : Suites latérales personnelles (4 piles).
Lorsqu'on pioche une carte dans la crapette ou le talon, il faut retourner la suivante, face visible.
Si le talon est épuisé, l'écart est retourné sans mélange pour en faire le nouveau talon.
Lorsqu'on pioche dans les suites latérales, seule la carte en sommet de pile peut être déplacée.
Destinations de pose :
- Priorité absolue : les suites centrales (8 piles).
- Destinations secondaires : Les suites latérales (8 piles, personnelles ou adverses) et les tas adverses (crapette ou écart).
Les cartes sont toujours posées ou déplacées une par une.
Les cartes des suites latérales doivent toutes être visibles, la carte posée ne recouvrant pas entièrement la précédente.
Les suites latérales ne peuvent être réorganisées que par déplacements successifs de cartes situées au sommet des piles. Une case vide peut recevoir n'importe quelle carte.
Cas de faute :
Il y a faute chaque fois qu'un joueur viole l'une des règles ci-dessus, à savoir :
- Oublie de poser sur les suites centrales en priorité
- Pioche une carte du talon alors qu'il peut placer une carte de la crapette
- Pioche une carte de l'écart alors qu'il peut placer une carte du talon ou de la crapette
A chaque faute, l'adversaire crie "crapette !". Le joueur laisse le jeu en l'état, pose la carte en faute sur son écart et passe le tour à l'adversaire.
Variantes usuelles :
1. Variante sans ordre de pioche : L'ordre de pioche (crapette, talon, écart) est supprimé. Le joueur peut piocher librement dans n'importe quel tas. Cette variante privilégie la fluidité et l'optimisation des suites au détriment de la contrainte classique de priorité, transformant la crapette en un jeu plus libre et plus tactique.
2. Variante avec suites latérales communes : Les piles latérales sont communes et non propres aux deux joueurs, donc sans la distinction personnelles/adverses. Les piles latérales sont manipulables par les deux joueurs. Cette variante augmente considérablement le niveau tactique et le potentiel de réagencement des piles.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante à la crapette. Mais il existe un ensemble de principes directeurs à mettre en oeuvre selon l'ordre hiérarchique suivant [PER][CHA] :
1. Poser sur les piles centrales afin d'éviter la faute et d'avancer le jeu central.
2. Créer un maximum de case vides dans les suites latérales par deux moyens possibles : restructurer les suites latérales (souvent jusqu'à fusionner plusieurs courtes en une seule longue), et charger les deux tas de l'adversaire.
3. Libérer sa crapette en accompagnant quand c'est possible la carte de crapette avec celle du talon ou de l'écart, sauf si cette libération
donne à l'adversaire une restructuration favorable.
B7.3.4. Le poker :

Le poker est un jeu de cartes stratégique pratiqué par 2 à 10 joueurs, avec un paquet standard de 52 cartes.
Son but principal est de remporter les mises (le "pot"), soit en formant la meilleure combinaison de cinq cartes, soit en poussant les adversaires à se coucher grâce au bluff.
Les 4 variantes de poker les plus jouées dans le monde sont le Texas Hold'em, l'Omaha, le 7-Card Stud et le 5-Card Draw.
Une partie désigne l'ensemble des manches jouées à une table, tandis qu'une manche correspond à un coup complet, depuis la mise initiale jusqu'à l'attribution du pot.
Attention : en anglais, le mot "hand" peut désigner soit la main de cartes (combinaison), soit la manche d'une partie (coup).
Types et valeurs des cartes :
Deux types de cartes sont possibles :
- les cartes privées, propres à chaque joueur, pouvant être cachées dites "fermées" (visibles uniquement par lui) ou visibles dites "ouvertes" (révélées aux autres joueurs),
- les cartes communes, visibles et utilisables par tous les joueurs.
Selon la variante, les cartes distribuées se répartissent comme suit :
- Texas Hold'em : 2 cartes privées cachées et 5 cartes communes.
- Omaha : 4 cartes privées cachées et 5 cartes communes
- 7-Card Stud : 3 cartes privées cachées et 4 cartes privées visibles.
- 5-Card Draw (ou "poker fermé") : 5 cartes privées cachées, révélées uniquement à l'abattage des cartes.
Les valeurs des cartes sont les suivantes, classées par ordre croissant de force :
2, 3, 4, ... , 10, Valet (J), Dame (Q), Roi (K), As (A), l'As pouvant compter pour 1 dans les suites autorisées (par exemple : As-2-3-4-5).
Dans les parties à 4 ou 5 joueurs, il est courant d'éliminer les 2, 3 et 4, ce qui réduit le jeu à 40 cartes.
Hiérarchie des mains [WIK9] :
La hiérarchie dans la force des mains est la suivante, avec leur probabilité d'apparition pour un jeu de 52 cartes selon deux cas :
- Liste 1 : tirage de 5 cartes au hasard, typique de la variante 5-Card Draw.
- Liste 2 : meilleure main parmi 7 cartes, pour les variantes Texas Hold'em, Omaha et 7-Card Stud.
Cette hiérarchie reste la même dans toutes les variantes de poker. Seules leurs probabilités d'apparition varient, en fonction du nombre de cartes distribuées et de celles pouvant être combinées pour former la meilleure main.
Chaque main est définie par son critère minimal, la hiérarchie des mains se chargeant de départager automatiquement les cas de recouvrement.
| Main | Définition | Exemple | Cas d'égalité | Probabilité Liste 1 | Probabilité Liste 2 |
|---|---|---|---|---|---|
| Quinte flush royale | Quinte flush dont la carte la plus haute est l'As | 10 J Q K A | impossible | 0,00015 % | 0,0032 % |
| Quinte flush | 5 cartes de valeurs consécutives et de même couleur, avec As autorisé en carte basse | 8 9 10 J Q | carte la plus haute | 0,0014 % | 0,028 % |
| Carré | 4 cartes de même valeur | Q Q Q Q | valeur du carré, puis carte restante | 0,024 % | 0,17 % |
| Full | Brelan + paire | 10 10 10 K K | valeur du Brelan, puis paire la plus haute | 0,14 % | 2,60 % |
| Couleur (ou Flush) | 5 cartes de même couleur | 8 9 10 J K | cartes en ordre décroissant | 0,20 % | 3,03 % |
| Quinte (ou Straight) | 5 cartes de valeurs consécutives, avec As autorisé en carte basse | 8 9 10 J Q | carte la plus haute | 0,39 % | 4,6 % |
| Brelan | 3 cartes de même valeur | 10 10 10 | valeur du Brelan, puis cartes restantes en ordre décroissant | 2,11 % | 4,83 % |
| Deux paires | deux paires | K K 8 8 | paire la plus haute, puis deuxième paire, puis carte restante | 4,75 % | 23,50 % |
| Une paire | 2 cartes de même valeur | K K | paire la plus haute, puis cartes restantes en ordre décroissant | 42,26 % | 43,82 % |
| Carte haute | Aucune des mains précédentes | A J 9 6 2 | cartes en ordre décroissant | 50,12 % | 17,41 % |
| Total | 100,00 % | 100,00 % |
A noter dans ce tableau :
- La couleur n'affecte pas la force intrinsèque d'une main dans la hiérarchie par rapport aux autres mains, sauf pour former une Couleur, une Quinte flush ou une Quinte flush royale. Entre elles, les couleurs sont équivalentes et neutres, sauf pour départager des égalités dans certaines variantes non standard.
- Les probabilités n'augmentent pas toujours strictement avec la faiblesse de la main, mais l'ordre hiérarchique reste correct pour déterminer le gagnant.
Droit d'entrée (la cave) :
La cave est le montant que chaque joueur engage pour participer à la partie.
- Au début de la partie, le joueur achète des jetons correspondant à sa cave.
-
Pendant la partie, toutes les mises et relances se font uniquement avec des jetons.
- A la fin, le joueur échangera ses jetons contre de l'argent selon leur valeur.
Mise avant distribution des cartes (mise initiale) :
Avant toute distribution de cartes, une mise obligatoire est imposée afin de constituer le pot de départ.
Elle prend la forme d'antes (tous les joueurs misent) ou de blinds (mises forcées de certains joueurs), et est effectuée sans connaissance des cartes.
Ante :
L'ante est une mise identique obligatoire placée par chaque joueur avant la distribution des cartes pour créer un pot initial.
Elle est obligatoire dans la variante 7-Card Stud et facultative dans 5-Card Draw.
Blind :
Les blinds sont des mises forcées placées avant la distribution des cartes pour créer un pot initial.
Elles sont obligatoires dans les variantes Texas Hold'em et Omaha, et peuvent se cumuler avec des antes selon les spécificités de la partie.
Deux types de blind existent :
-
Small Blind (SB) : petite mise, placée par le joueur immédiatement à gauche du bouton (donneur).
-
Big Blind (BB) : mise complète (généralement le double de SB), placée par le joueur à gauche du Small Blind.
Les autres joueurs, hors SB et BB, ne misent rien au départ.
Le sur-blind (ou straddle)
est une mise facultative supplémentaire (généralement le double de BB), placée par le joueur situé à gauche du Big Blind.
Il donne un avantage stratégique en permettant au joueur qui le place d'agir en position tardive sur le premier tour, d'augmenter le pot initial et de mettre la pression sur ses adversaires.
Distribution des cartes (la donne) :
Les cartes sont données une par une, dans le sens horaire, à partir du joueur à gauche du donneur, selon la variante jouée.
Le rôle de donneur tourne à chaque manche de jeu.
Déroulement du jeu :
Après la donne, les joueurs misent par tours d'enchères successifs, selon les étapes prévues par la variante.
L'action consiste à prendre une décision : se coucher, suivre ou relancer.
Elle commence par le joueur à gauche des blinds lors des tours d'enchères et suit le sens horaire.
Sans blinds, on part du joueur à gauche du donneur (5-Card Draw) ou de la carte la plus faible visible (7-Card Stud).
Le principe de base des enchères est qu'un joueur doit "suivre" en engageant le même montant que la mise la plus élevée pour rester dans la manche. S'il ne le fait pas, il "se couche" et perd ses mises géjà engagées. Il peut également "relancer", c'est-à-dire augmenter la mise, obligeant alors les autres joueurs à suivre, relancer ou se coucher.
Le tour d'enchères se termine lorsque tous les joueurs encore en lice ont, soit abandonné, soit égalisé la mise la plus élevée.
Tours d'enchères :
Une manche comprend plusieurs tours d'enchères selon les variantes.
Pour chaque tour, le nombre de cartes indiqué ci-dessous est le nombre de cartes distribuées, révélées, ajoutées ou échangées, mises à la disposition du joueur, qu'il s'agisse de cartes privées ou communes.
Texas Hold'em et Omaha : 4 tours
- Préflop : 2 cartes privées pour Texas Hold'em et 4 pour Omaha
-
Flop : 3 cartes communes
-
Turn : quatrième carte commune
-
River : cinquième et dernière carte commune
7-Card Stud : 5 tours
- 3rd Street : 3 cartes (2 cachées, 1 visible)
-
4th Street : 1 carte visible
- 5th Street : 1 carte visible
-
6th Street : 1 carte visible
-
7th Street : 1 carte cachée
5-Card Draw : 2 tours
- Après la donne : 5 cartes
- Après l'échange : 0 à 5 cartes
Echange de cartes :
Selon la variante, un joueur peut ou non échanger des cartes qui sont tirées du sabot par le donneur ou par le croupier en casino.
Dans les variantes de type Draw (notamment le 5-Card Draw), un échange de cartes est autorisé après le premier tour d'enchères.
Dans les autres variantes courantes (Texas Hold'em, Omaha, 7-Card Stud), aucun échange n'est possible : les cartes sont uniquement distribuées par la donne.
Fin de manche :
La manche se termine, soit par l'abandon de tous les joueurs sauf un, lequel remporte le pot, soit par l'abattage des cartes après le dernier tour d'enchères.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au poker, mais il existe une stratégie optimale pour débutants qui consiste à respecter les principes suivants [PER][CHA] :
1. Jouer pour l'espérance
: Une décision est bonne si elle est rentable à long terme, même si elle conduit parfois à une perte immédiate.
2. Adapter sa stratégie à sa position : Il faut jouer prudemment lorsqu'on agit tôt dans les tours d'enchères, et agressivement en exploitant l'information disponible lorsqu'on agit tard, idéalement en dernier.
3. Adapter ses mises à la situation : Il faut miser gros lorsqu'on a de bonnes cartes ou pour protéger le pot, et miser peu ou se coucher dans le cas contraire.
4.
Bluffer intelligemment : Il faut bluffer juste assez pour rendre l'adversaire indifférent entre suivre et se coucher.
5. Jouer les adversaires : Il faut bluffer plus contre les joueurs prudents et moins contre les suiveurs.
6. Gérer sa cave : Il ne faut jamais risquer trop sur une seule manche et savoir quitter la table à temps.
7. Jouer serré : Pour une stratégie volontairement prudente, il faut participer à seulement 20 % environ des manches d'une partie, d'où la règle ultra-simple selon la variante :
- 5-Card Draw : Se coucher à moins d'avoir une paire haute (JJ, QQ, KK ou AA), ou mieux, dès la donne.
- Texas Hold'em : Se coucher à moins d'avoir une paire, un As accompagné d'une carte haute, ou deux cartes consécutives de même couleur (connecteurs suited), au Préflop.
- Omaha : Se coucher à moins d'avoir deux mains Flush possibles avec des cartes de même couleur (double tirage suited), ou une paire forte (AA ou KK), au Préflop.
- 7-Card Stud : Se coucher à moins d'avoir une paire haute cachée ou trois cartes pouvant former une Quinte ou une Couleur, après la troisième carte.
B7.4. Jeux avec dés :
Les jeux de dés suivants sont des jeux mêlant hasard et stratégie.
B7.4.1. Le jeu du 101 :

Le jeu du 101, appelé également Pig ou jeu du Porc, est un jeu de dés simple pour deux ou plusieurs joueurs, mêlant hasard et stratégie.
Attention à ne pas confondre avec le jeu du "Cochon qui rit" (jeu d'assemblage d'un cochon miniature ou dessiné) ou le jeu de "cochons" (ou "Pass the Pigs" : figurines de cochons utilisées comme dés).
Le jeu repose sur un équilibre entre prise de risque et prudence, chaque joueur devant choisir le bon moment pour s'arrêter avant qu'un 1 ne vienne tout annuler.
Le jeu nécessite un dé classique à six faces, une feuille de papier et un crayon pour noter les scores.
Les règles du jeu usuel sont les suivantes [WIK6] :
Configuration initiale :
Le score total de chaque joueur commence à 0.
Objectif :
Les joueurs jouent à tour de rôle.
A son tour, le joueur lance le dé autant de fois qu'il le souhaite.
Tant que la face obtenue est différente de 1, il ajoute la valeur obtenue aux points du tour.
Il peut alors choisir de relancer pour tenter de gagner plus ou s'arrêter pour sécuriser les points du tour et les ajouter à son score total.
En revanche, s'il obtient un 1, tous les points du tour sont perdus (mais pas les points du score total) et son tour s'arrête immédiatement.
Le joueur gagnant est celui qui atteint ou dépasse 101 points au score total, à la fin de son tour.
Variante :
Une variante sévère consiste à remettre le score total du joueur à 0 lorsqu'il obtient un 1.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au jeu du 101 car le hasard domine. Mais il existe une stratégie optimale fondée sur l'analyse mathématique des probabilités, selon les règles suivantes [PER][CHA].
1. Le nombre optimal de points à viser par tour est d'environ 20 points (seuil optimal pour maximiser l'espérance du gain).
2. Ce seuil est à diminuer à mesure que le score total approche de 101 afin de réduire le risque face à l'adversaire : typiquement 15 points à partir d'un score total de 75 points, puis 10 points à partir de 91 points.
Ces seuils proviennent de l'analyse mathématique par tour isolé : chaque relance a une espérance positive de gain, mais également un risque de 1/6 de perdre l'intégralité des points du tour. Cette espérance devient défavorable lorsque les points accumulés dans le tour approchent 20.
Démonstration :
La valeur moyenne d'un lancer, conditionnellement au fait de ne pas faire 1, est : (2 + 3 + 4 + 5 + 6)/5 = 4
La probabilité de ne pas obtenir 1 est : 5/6
L'espérance brute d'un lancer supplémentaire est donc : (5/6) x 4
Mais il faut tenir compte du risque de perdre les points déjà accumulés dans le tour. Si le joueur a déjà T points dans le tour, l'espérance nette E(T) d'une relance est : E(T) = (5/6) x 4 - (1/6) x T = 3,33 - T/6
La relance reste donc favorable tant que : T < 20
B7.4.2. Le Yam's :
Le Yam's, ou Yahtzee, est un jeu de dés pour un ou plusieurs joueurs, mêlant hasard et stratégie.
Chaque joueur cherche à réaliser des combinaisons de dés pour maximiser son score sur une grille de scores dédiée.
Le jeu trouve son origine au Canada dans les années 1950, sous le nom "Yacht Game". Il aurait été créé par un couple qui le faisait découvrir à ses invités lors de croisières en yacht. Le jeu a ensuite été popularisé et commercialisé en 1956 sous le nom Yahtzee par Edwin S. Lowe.
Le jeu nécessite 5 dés classiques à six faces, une feuille de papier et un crayon pour noter les scores.
Les règles du jeu ordinaire (familial) sont les suivantes [PER][CHA] :
Configuration initiale :
La grille de scores comporte autant de colonnes que de joueurs, et autant de lignes que de combinaisons possibles (voir Figure ci-dessus).
Les lignes sont réparties en deux parties :
- Partie supérieure (ou mineure) : Chaque ligne correspond à une valeur de dé (As, Deux, ..., Six).
As : somme des faces identiques montrant un As. Score = cette somme (exemple : 1-1-1-1-6 donne 4 points).
Deux : somme des faces identiques montrant un 2. Score = cette somme.
Trois : somme des faces identiques montrant un 3. Score = cette somme.
Quatre : somme des faces identiques montrant un 4. Score = cette somme.
Cinq : somme des faces identiques montrant un 5. Score = cette somme.
Six : somme des faces identiques montrant un 6. Score = cette somme.
Total : total des six scores ci-dessus.
Bonus : +35 points si Total ≥ 63 points.
Total 1 : Total + Bonus
- Partie inférieure (ou majeure) :
Brelan : au moins 3 faces identiques. Score = total de ces faces (exemple : 2-2-2 donne 6 points).
Carré : au moins 4 faces identiques. Score = total de ces faces (exemple : 3-3-3-3 donne 12 points).
Full : Un triplet et une paire de faces identiques (exemple : 3-3-3-6-6). Score = 25 points.
Petite suite : au moins 4 faces qui se suivent (exemple : 2-3-4-5). Score = 30 points.
Grande suite : au moins 5 faces qui se suivent (exemple : 2-3-4-5-6). Score = 40 points.
Yam's (ou Quine) : 5 faces identiques (exemple : 4-4-4-4-4). Score = 50 points.
Chance (ou Joker) : toute combinaison. Score = total des cinq faces. Cette combinaison permet de sauver un tour en évitant de barrer une combinaison.
Total 2 : total des sept scores ci-dessus.
Score final : Total 1 + Total 2
Objectif :
Les joueurs jouent à tour de rôle.
A son tour, le joueur lance les cinq dés, sans dépasser trois lancers successifs au total (le premier plus deux relances optionnelles).
Après chaque lancer, il peut reprendre tous ou partie des dés, selon son gré, pour tenter d'obtenir la combinaison voulue.
A la fin de son tour, il remplit obligatoirement une des cases vides de la grille.
Si aucune combinaison n'est possible ou jugée intéressante, il doit barrer une combinaison de son choix.
La partie se termine au bout de 13 tours correspondant aux 13 combinaisons, lorsque toutes les cases de la grille sont remplies pour tous les joueurs.
Le joueur gagnant est celui qui a obtenu le score le plus élevé dans la ligne Score final de la grille.
Variante - Blocage des lignes de la partie supérieure :
Lorsqu'un joueur obtient le score maximum possible dans une ligne de la partie supérieure, cette ligne devient inaccessible aux autres joueurs pour le reste de la partie.
Par exemple, un joueur réalise 3-3-3-3-3 dans la combinaison Trois. La ligne Trois est alors barrée pour tous les autres joueurs.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au Yam's car le hasard domine. Mais il existe une stratégie optimale basée sur les règles suivantes [PER][CHA].
1. Partie supérieure : Viser le Bonus de 35 points et le blocage des lignes de la partie supérieure.
2. Scores variables (Partie supérieure, Brelan, Carré) : toujours relancer jusqu'au 3ème lancer pour maximiser le score.
3. Scores fixes (Full, Petite suite, Grande suite) : s'arrêter immédiatement dès que la combinaison est obtenue.
4. Ligne Chance : La réserver pour des scores élevés, ou en dernier recours pour éviter de barrer une combinaison.
5. Stratégie globale (timing) :
- En début de partie (tours 1 à 4), viser en priorité les scores fixes (Full, Petite suite, Grande suite) qui sont relativement accessibles et libèrent la partie supérieure pour plus tard.
- En milieu de partie (tours 5 à 9), viser les scores variables (Partie supérieure, Brelan, Carré) pour accumuler des scores élevés, y compris le Bonus.
- En fin de partie (tours 10 à 13), viser Yam's et Chance avec scores élevés afin de maximiser le Score final ou de sauver les dernières cases vides.
B7.5. Jeux sur feuille de papier :
Les jeux suivants, faciles à mettre en place avec une simple feuille et un crayon, mettent en oeuvre des stratégies basées sur le contrôle de l'espace de jeu.
B7.5.1. La bataille navale :
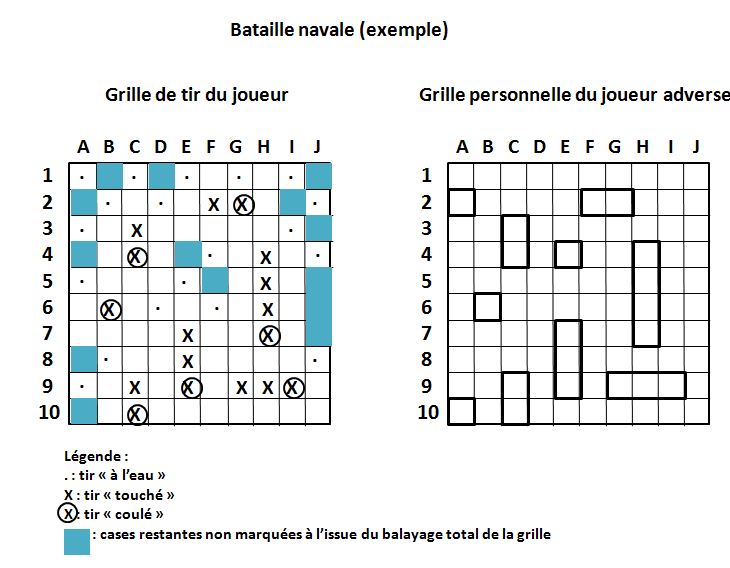
La bataille navale, appelée aussi touché-coulé, est un jeu de société dans lequel deux joueurs doivent placer des "bateaux" sur une grille tenue secrète et tenter de "toucher" les bateaux adverses.
Les règles du jeu usuel en France et en Belgique sont les suivantes [WIK2] :
Configuration initiale :
Chaque joueur dispose de deux grilles quadrillées 10 x 10 et numérotées comme les grilles de mots croisés (en France : lignes de haut en bas de 1 à 10 et colonnes de gauche à droite de A à J).
Chaque joueur dispose aussi d'une flotte composée de 10 bateaux symbolisés par des rectangles d'une à quatre cases de long, comme suit :
- 1 grand bateau de 4 cases
- 2 bateaux moyens de 3 cases
- 3 bateaux moyens de 2 cases
- 4 petits bateaux de 1 case
Les formes en L, en T, en carré, en zigzag ou discontinues sont interdites.
L'une des grilles (grille personnelle) représente la zone contenant sa propre flotte. Au début du jeu, chaque joueur place tous les bateaux sur sa grille, verticalement ou horizontalement, en dessinant chaque bateau par un rectangle plus appuyé.
Deux bateaux doivent être séparés d'au moins une case et sans se toucher par un coin. Les cases non occupées représentent l'eau.
L'autre grille (grille de tir) représente la zone adverse, où chaque joueur cherchera à couler les bateaux de son adversaire.
Objectif :
Les joueurs jouent à tour de rôle en annonçant une case (par exemple "B6"). L'adversaire répond obligatoirement par l'une des annonces suivantes :
- "A l'eau" si le tir tombe à l'eau
- "Touché" si le tir touche un bateau en laissant des cases intactes
- "Coulé" si le tir touche la dernière case intacte d'un bateau
Sur sa grille de tir, le joueur marque :
- un point (.) pour un tir "à l'eau"
- une croix (X) pour un tir "touché"
- une croix cerclée (⊕) pour un tir "coulé". Juste après ce tir, le joueur doit également marquer par un point (.) toutes les cases non déjà marquées entourant le bateau coulé afin de matérialiser la règle de non-contact.
Le gagnant est celui qui parvient le premier à "couler" tous les bateaux de l'adversaire.
Exemple :
La Figure ci-dessus montre un exemple de bataille navale, avec grille personnelle du joueur adverse (non connue du joueur) et grille de tir du joueur.
Le premier tir est réalisé sur la case A1. Les suivants se succèdent ligne après ligne, de gauche à droite, et de haut en bas, selon la stratégie optimale (voir ci-dessous).
Pour ne pas alourdir la Figure, la grille de tir ne comporte pas les marques supplémentaires (.) posées sur les cases non marquées entourant les bateaux coulés, juste après un tir "coulé".
A l'issue du balayage total de cette grille de tir, tous les bateaux de taille 2 cases ou plus sont coulés. Ne restent que 3 petits bateaux de taille 1 case (A2, E4 et A10) à trouver ensuite en 14 tirs maximum (cases grisées sur la Figure).
Variante :
Chaque joueur tire une salve de trois tirs successifs. Cette variante accélère la partie.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante à la bataille navale. Mais il existe une stratégie optimale basée sur les règles suivantes [PER][CHA] :
1. Phase de placement : Dispersion maximale.
- Répartir les bateaux sur toute la grille afin de limiter les corrélations spatiales et rendre toute information locale peu exploitable.
- Privilégier le centre de la grille. Les cases centrales
autorisent davantage de placements possibles, ce qui
permet aux bateaux de se fondre dans l'incertitude (camouflage statistique).
- Eviter les coins et les regroupements. En exploration intuitive, ces zones font l'objet d'un ciblage préférentiel psychologique ("zones suspectes"). En exploration systématique (maillage, damier), les coins sont atteints en tirs précoces et les regroupements favorisent des tirs concentrés susceptibles de déclencher l'abandon de la recherche systématique au profit d'une fouille ciblée.
2. Phase de recherche : Nombre de tirs minimum.
- Colorier mentalement la grille adverse selon un damier comportant des cases noires et blanches alternées (comme sur un jeu de dames).
- Choisir une couleur puis balayer exhaustivement les cases de cette couleur, en tirant uniquement sur les cases non déjà marquées par (.),(X) ou (⊕).
- Dès qu'un tir est annoncé "touché", abandonner la recherche et passer en phase de poursuite.
- Ce balayage en 50 tirs maximum permet de couler tous les bateaux de taille 2 cases ou plus.
- A l'issue de ce balayage, rechercher les bateaux restants de taille 1 case, en tirant au hasard sur les n cases restantes non marquées (n = 15 en moyenne). Le nombre moyen de tirs (E) pour trouver les k bateaux restants est alors de 12 tirs si k = 3 (selon la formule E = k (n + 1)/(k +1)).
3. Phase de poursuite (après un "touché") : Pugnacité.
- Tirer immédiatement sur les cases adjacentes orthogonales afin de localiser et détruire le bateau touché.
- Déterminer l'orientation du bateau (vertical ou horizontal) dès le deuxième touché.
- Continuer dans la direction correspondante jusqu'à destruction complète du bateau.
- Ne jamais revenir à la recherche globale tant que le bateau n'est pas coulé.
B7.5.2. Le jeu de Zip :
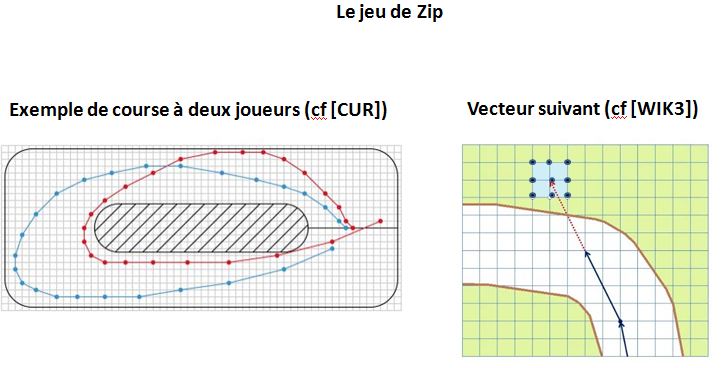
Le jeu de Zip, ou Formule 1, ou Course sur papier, ou Racetrack, popularisé par Martin Gardner en 1973, est un jeu ludique dans lequel un ou plusieurs joueurs réalisent une course de vitesse sur une piste dessinée sur papier quadrillé, en faisant intervenir de manière réaliste les contraintes d'accélération et de freinage.
Les règles du jeu de base sont les suivantes [WIK3] :
Configuration initiale :
Le jeu nécessite une feuille de papier quadrillée (à grand carreaux si possible), une gomme et un crayon par joueur (de couleurs différentes si possible).
La piste est dessinée sur la feuille selon deux bords sinueux plus ou moins parallèles, terminés par une ligne droite de départ, large d'autant de carreaux qu'il y a de joueurs, et une ligne d'arrivée.
Les bords de piste peuvent être uniquement des segments de droite. Cela évite d'avoir à trancher des situations litigieuses.
La piste peut être aussi une boucle fermée avec même ligne de départ et d'arrivée (voir Figure ci-dessus).
Chaque joueur marque au crayon la position de départ de sa voiture, qui est un des points de quadrillage sur la ligne de départ.
Objectif :
Les joueurs jouent ensuite à tour de rôle.
Le gagnant est le premier joueur à toucher ou franchir la ligne d'arrivée.
Règles de déplacement :
1. Tout déplacement menant sur une position déjà occupée par un autre joueur est interdit.
2. Le premier déplacement se fait d'une case vers l'avant de la piste, représenté par un vecteur reliant le point de départ à l'un de ses trois points voisins situés dans le sens de la course.
3. A chaque coup, le joueur prolonge le déplacement précédent en reportant le vecteur depuis sa position actuelle.
Le point obtenu est appelé point principal. Le joueur peux également choisir de se déplacer sur l'un des huit points voisins du point principal (voir Figure ci-dessus). Ces choix simulent l'accélération ou le freinage maximum autorisé compte-tenu de l'inertie de la voiture.
Cas de faute :
1. Lorsqu'un joueur sort de la piste en franchissant l'un des bords, l'un des deux types de pénalités peut être appliqué au tour suivant (à convenir en début de partie) :
- Pénalité douce (avec freinage d'urgence) : Le joueur passe son tour. Au tour suivant, le vecteur correspondant à la sortie de piste est remis à zéro. Le joueur redémarre en se se déplaçant sur l'un des huit points voisins de sa position (point principal confondu avec la position courante). Cette règle sanctionne l'erreur sans élimer le joueur de la course, en lui offrant une seconde chance de gagner.
- Pénalité stricte (avec course de récupération) : Le joueur doit réintégrer la piste en franchissant le bord en un point situé derrière celui où il a quitté la piste. Plus la vitesse est grande au moment de la sortie, plus le nombre de mouvements pour revenir sur la piste est élevé. Cette règle réduit considérablement les chances de gagner après une erreur.
2. Sur certaines pistes très sinueuses, il peut arriver qu'un déplacement hors piste corresponde à un vecteur qui coupe deux fois le bord de la piste, avec un point de départ et un point d'arrivée tous deux situés à l'intérieur de la piste. Ce type de "raccourci hasardeux" est autorisé et ne constitue pas une sortie de piste.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au jeu de Zip. Mais il existe une stratégie optimale basée sur les règles suivantes [PER][CHA] :
1. Anticiper les virages en ralentissant progressivement pour maximiser la vitesse moyenne sur l'ensemble de la course.
2. Eviter les accélérations et les changements de direction brusques afin de réduire les risques de sortie de piste.
3. Dans les virages, négocier les courbes comme le fait un pilote automobile : approcher le virage en cotoyant le bord extérieur de la piste. Pendant le virage, maintenir cette trajectoire tant que la sortie du virage n'est pas visible. Puis couper progressivement le virage pour rejoindre la ligne droite. Cette trajectoire minimise la distance parcourue dans la courbe et aide à préserver une vitesse de sortie élevée.
B7.5.3. Le morpion 10 x 10 :

Le morpion 10 x 10, ou "Tic-tac-Toe étendu", est un jeu stratégique pour deux joueurs, dont le but est d'être le premier à aligner une série de 5 symboles identiques sur une grille 10 x 10.
Les règles du jeu de base sont les suivantes [WIK7] :
Configuration initiale :
Le jeu nécessite une feuille de papier quadrillée (de taille 10 x 10 en général) et un crayon par joueur.
La grille est vide au début de la partie.
Chaque joueur choisit un symbole distinct : X ou O
Le joueur X commence toujours la partie et a donc un avantage, non pas géographique (position sur la grille), mais fonctionnel (rôle offensif avec toujours un coup d'avance).
Pour rétablir l'équilibre, on peut appliquer la "pie rule". Après le premier coup de X, le joueur O choisit soit de conserver son rôle O, soit d'échanger les symboles (il devient X et son adversaire devient O). Selon la qualité du premier coup ou sa préférence personnelle, le joueur O peut ainsi choisir librement son rôle (offensif ou défensif) pour la suite de la partie, chaque rôle présentant un intérêt selon le style de jeu du joueur.
Objectif :
Les joueurs jouent à tour de rôle.
A son tour, le joueur
place un seul symbole dans une case vide. Le symbole est définitif et ne peut pas être retiré ou déplacé.
Le joueur gagnant est celui qui crée le premier un alignement d'au moins 5 symboles identiques consécutifs, horizontalement, verticalement ou en diagonale (voir exemple de début de partie sur Figure ci-dessus).
Si la grille est entièrement remplie sans aucun alignement formé, la partie est déclarée nulle.
Variante :
La partie se termine lorsque la grille est entièrement remplie. Le gagnant est le joueur ayant réalisé le plus grand nombre d'alignements gagnants.
Un alignement gagnant est une série d'au moins 5 symboles identiques consécutifs sans interruption (les alignements de 6 ou plus sont également gagnants). Les séries, courtes ou longues, comptent comme un seul alignement et ne peuvent ni se chevaucher ni se croiser.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au morpion 10 x 10. Mais il existe une stratégie optimale basée sur les règles suivantes [PER][CHA] :
Règles à prioriser dans l'ordre suivant (Légende : 'X' pour le joueur, 'O' pour l'adversaire, '_' pour une case vide) :
1. Victoire immédiate : Compléter un XXXX_ ou XXX_X ou XX_XX ou X_XXX
2. Défaite écartée : Bloquer impérativement un OOOO_ ou OOO_O ou OO_OO ou O_OOO
3. Fourchette écartée : Bloquer impérativement une fourchette potentielle de l'adversaire.
4. Attaque double (fourchette) : Placer un X créant simultanément deux menaces immédiates dans deux lignes distinctes, chacune formant un alignement de quatre X avec une case libre située soit en extrémité, soit à l'intérieur de l'alignement.
5. Attaque simple : Créer un XXXX_ ou XXX_X ou XX_XX ou X_XXX
6. Prolonger les alignements (plutôt que jouer isolé).
7. Privilégier le centre de la grille et les intersections (cases vides situées au croisement de deux ou plusieurs alignements existants).
B7.5.4. Tic-tac-toe :
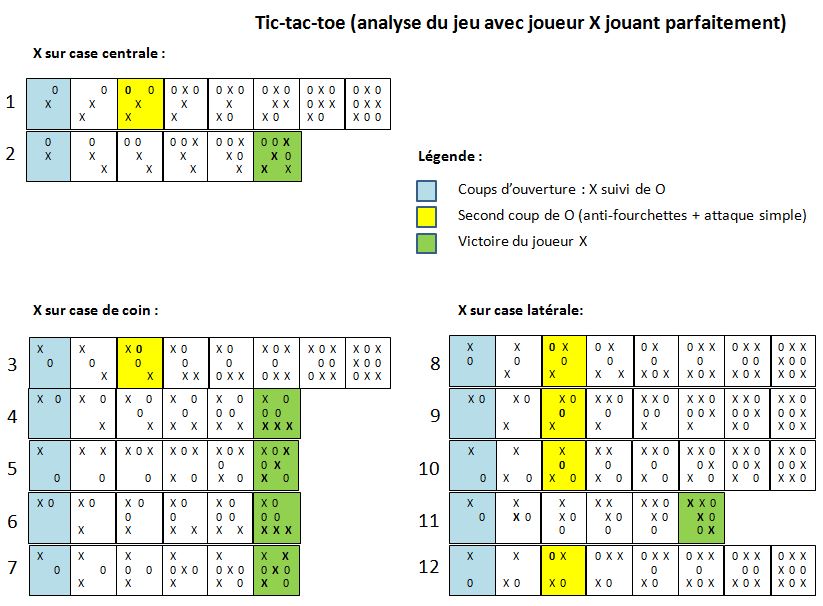
Tic-tac-toe est une version standard réduite du jeu de morpion 10 x 10 [WIK8]. Les différences avec la version 10 x 10 sont les suivantes :
- Grille de taille 3 x 3 (au lieu de 10 x 10) avec un repérage des cases réduit (A1, A2, A3, B1, B2, B3, C1, C2, C3).
- Alignement de 3 symboles identiques (au lieu de 5 symboles identiques consécutifs au moins).
- Remplacement possible de la règle d'équilibre "pie rule" par la règle où chaque joueur joue deux parties, une en tant que X et une en tant que O. Le gagnant est celui qui remporte au moins une des deux parties sans en perdre aucune. Dans tous les autres cas, le match est déclaré nul.
- Victoire au premier alignement (la variante consistant à compter le nombre d'alignements est exclue).
- Stratégie optimale particulière due à la présence immédiate des bords de grille (voir ci-dessous).
Analyse du jeu :
Si les deux joueurs jouent parfaitement, la partie se termine toujours par un match nul.
Le joueur X commence la partie. Son premier coup peut appartenir à trois classes de positions distinctes sur la grille : la case centrale, l'un des coins ou l'une des cases latérales.
Le joueur O répond avec un coup qui peut appartenir à cinq classes de positions distinctes : la case centrale, l'un des coins (adjacent ou distant de la case X) ou l'une des cases latérales (adjacente ou distante de la case X).
Ce qui fait 12 cas possibles hors cases équivalentes par symétrie (voir Figure ci-dessus), avec les résultats suivants lorsque le joueur X joue parfaitement :
- Si X joue la case centrale, alors la partie est gagnée par X si O joue par erreur une case latérale (cas 2 de la Figure), et nulle dans le cas contraire (O joue une case de coin).
- Si X joue une case de coin, alors la partie est gagnée par X si O joue par erreur une case de coin ou latérale (cas 4 à 7 de la Figure), et nulle dans le cas contraire (O joue la case centrale).
- Si X joue une case latérale, alors la partie est gagnée par X si O joue par erreur une case latérale adjacente à celle de X (cas 11 de la Figure), et nulle dans le cas contraire (O joue la case centrale, une case de coin ou la case latérale opposée à celle de X).
Les stratégies d'ouverture optimale pour chaque joueur sont alors les suivantes :
* Joueur X :
- Pour éviter des cas défavorables (en particulier le cas 11 : X latéral suivi de O latéral adjacente à X),
X doit jouer en premier soit la case centrale, soit l'un des coins (cas 1 à 7).
- Dans la majorité des réponses possibles de O (cas 2, 4, 5, 6 et 7), cette ouverture place X dans une position pratiquement gagnante.
- Dans les autres cas (cas 1 et 3), X laisse à O une situation défensive délicate dès son second coup, où O doit jouer un coup souvent unique combinant prévention des fourchettes et attaque simple pour maintenir le match nul.
- Toute victoire de X repose donc sur une erreur de O.
* Joueur O :
- A son premier coup, O doit jouer la case centrale si elle est libre et, à défaut, l'un des coins adjacents à la case initiale X (cas 1, 3, 8, 9), ce qui écarte d'office certains cas défavorables. Cette stratégie garantit le match nul si les deux joueurs jouent parfaitement. Toute autre réponse peut conduire à une défaite de O.
- A son second coup, O doit impérativement jouer la case (souvent unique) qui, à la fois, neutralise toutes les fourchettes potentielles de X et le force à répondre à un alignement de O, lorsque ce forçage est possible (voir les cases mises en jaune sur la Figure).
- O est ainsi doublement désavantagé : pour obtenir le match nul, il doit jouer sans aucune erreur ses deux premiers coups critiques : le premier (centre ou coin adjacent) et le second (anti-fourchettes + attaque simple).
- Toute victoire de O nécessite donc une erreur de X.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au tic-tac-toe. Mais il existe une stratégie optimale basée sur les règles suivantes [PER][CHA] :
Règles à prioriser dans l'ordre suivant (Légende : 'X' pour le joueur, 'O' pour l'adversaire, '_' pour une case vide) :
1. Victoire immédiate : Compléter un XX_ ou X_X
2. Défaite écartée : Bloquer impérativement un OO_ ou O_O
3. Fourchette écartée : Bloquer impérativement une fourchette potentielle de l'adversaire.
4. Attaque double (fourchette) : Placer un X créant simultanément deux menaces immédiates dans deux lignes distinctes, chacune formant un alignement XX_ ou X_X
5. Attaque simple : Créer un XX_ ou X_X
B7.6. Jeux de loterie :
Les jeux de loterie, tels que le Loto, la roulette ou les machines à sous, forment une vaste famille de jeux d'argent où le hasard prime sur la stratégie. A long terme, le joueur subit des pertes inéluctables en raison d'une espérance mathématique négative.
En pourcentage approximatif du coût de participation, la perte moyenne du joueur par unité de mise (une grille ou un jeton) est en effet la suivante :
- Loto FDJ télévisé (60 %)
- EuroMillions (50 %)
- Ticket à gratter (45 %)
- Rapido (33 %)
- Boule (11 %)
- Roulette américaine - mise spéciale 5 numéros (8 %)
- Machine à sous classique à trois rouleaux (6 %)
- Roulette américaine - autres mises (5 %)
- Roulette française (3 à 1 % selon règles spéciales).
On observe ainsi que les loteries type Loto redistribuent peu aux joueurs, tandis que les casinos mieux structurés entraînent des pertes moindres, surtout sur la roulette française.
Attention : Les organismes de jeux annoncent souvent un taux de redistribution global par mise (TRG) calculé à partir des gains pondérés par leur probabilité.
Ce taux est doublement trompeur : arrondi à la hausse et surtout masquant la perte réelle du joueur. Par exemple, au jeu de Boule, le TRG de 90 % correspond en réalité à une espérance négative par mise (E = TRG - 1) de -11 %
B7.6.1. Le loto français :
Le loto français est un jeu de hasard individuel ou collectif, admettant une dimension stratégique très limitée.
Deux variantes principales existent :
- Loto traditionnel : pratiqué lors de fêtes locales ou dans un cadre associatif, avec des cartons de jeu de 90 numéros.
- Loto FDJ télévisé : proposé par la Française des Jeux (FDJ), avec des grilles de 49 numéros + 10 numéros pour le numéro Chance.
B7.6.1.1. Loto traditionnel [PER][CHA] :
Matériel :
-
Machine de tirage : boulier ou dispositif équivalent.
-
Boules : 90 boules numérotées de 1 à 90.
-
Cartons de jeu : carton prédéfini remis aux joueurs avant la partie (voir Figure ci-dessus).
-
Chaque carton contient 1 à 3 grilles.
-
Chaque grille = 3 lignes × 9 cases.
-
Chaque ligne = 5 numéros et 4 cases vides.
-
Certains cartons ont 2 lignes de 5 cases numérotées (1 à 10) en haut à gauche pour repérage administratif.
-
Tous les cartons et toutes les grilles participent au même tirage, mais les gains sont calculés par grille.
Remplissage des grilles :
- Les joueurs cochent sur leurs grilles les numéros tirés.
- Les cases vides ne doivent pas être cochées. Toute coche parasite entraîne l'invalidation de la grille.
- Chaque grille est indépendante. Utiliser plusieurs grilles multiplie simplement les chances de gagner.
Conditions de gain :
- Il y a gain dès qu'une des figures suivantes est obtenue sur une grille :
-
Quine : 5 numéros cochés sur une ligne horizontale.
-
Double quine : 10 numéros cochés sur deux lignes horizontales.
-
Grille pleine : 15 numéros cochés sur toute la grille.
- Seules les lignes horizontales comptent. Aucune autre configuration (verticale, diagonale) n'est valide.
- Les montants des gains pour une grille sont donnés par le tableau suivant :
| Figure | Gain (G) | probabilité (p) |
|---|---|---|
| Quine | défini par l'organisateur | 1/43 949 268 |
| Double quine | défini par l'organisateur | 1/(5,72 1012) |
| Grille pleine | défini par l'organisateur | 1/(4,58 1016) |
A noter dans ce tableau :
La probabilité (p) est la probabilité théorique minimale, correspondant à
une figure obtenue exactement au premier instant possible.
En pratique, le tirage se poursuit, ce qui augmente légèrement les probabilités. Par ailleurs, jouer plusieurs grilles augmente les probabilités de manière proportionnelle au nombre de grilles.
La probabilité (p) se calcule comme suit, avec n = nombre de numéros gagnants requis (5, 10 ou 15) :
p(n) = C(n, n) C(90 - n, 0) / C(90, n) = 1/C(90, n) avec :
Coefficient binomial C(a, b) = a! / (b! (a - b)!)
C(n, n) = 1 : nombre de façons de choisir les n numéros gagnants parmi les n numéros constituant la figure.
C(90 - n, 0) = 1 : nombre de façons de choisir zéro numéro perdant parmi les (90 - n) numéros restants.
C(90, n)
: nombre total de tirages possibles de n numéros parmi 90.
Les probabilités associées aux différentes figures (quine, double quine et grille pleine) sont donc extrêmement faibles, quasi nulles.
Déroulement du tirage :
- Les dates des tirages sont fixées par l'organisateur du loto.
- Chaque figure (quine, double quine, grille pleine) est associée à un nombre maximal de boules pouvant être tirées, typiquement : 40 pour la quine, puis 20 supplémentaires pour la double quine et 15 supplémentaires pour la grille pleine. Ces plafonds cumulatifs sont annoncés en début de soirée par l'organisateur.
- Le tirage commence après distribution des cartons.
- Les numéros sont tirés un à un, puis annoncés ou affichés.
- Un joueur pensant avoir une figure lève la main et l'annonce clairement.
- Le tirage est interrompu pour vérifier et valider les gains.
- Il se poursuit jusqu'à ce que toutes les figures prévues soient réalisées ou jusqu'à épuisement des 90 numéros.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au loto traditionnel. Contrairement au Loto FDJ où une gestion rationnelle du risque reste possible, le loto traditionnel n'offre aucune stratégie viable : ni choix de grille (carton fixe imposé), ni contrôle sur les tirages (séquentiels sans intervention).
Au vu des probabilités extrêmement faibles associées aux différentes figures, le loto traditionnel ne peut donc être considéré comme un jeu de gain, mais uniquement comme un jeu de divertissement collectif.
B7.6.1.2. Loto FDJ télévisé [PER][CHA] :
Matériel :
- Machine de tirage FDJ.
- Boules :
49 boules numérotées de 1 à 49 pour les 5 numéros principaux. Une boule complémentaire ("numéro Chance") est tirée ensuite parmi 10 boules numérotées de 1 à 10.
- Bulletins
de jeu : achetés dans les bureaux de tabac (voir Figure ci-dessus).
- Chaque bulletin contient 1 à plusieurs grilles à remplir librement par le joueur ou proposée automatiquement par le terminal FDJ (mode "FLASH").
- Chaque grille = 5 numéros choisis parmi 49, et 1 numéro optionnel ("numéro Chance") choisis parmi 10.
- Terminal FDJ dans les bureaux de tabac, disposant de deux entrées possibles (manuel/Flash), d'un lecteur scanner des bulletins et d'une sortie papier (reçu de participation et de preuve légale).
Remplissage des grilles :
-
Les joueurs remplissent leurs grilles avant le tirage.
- Chaque grille est indépendante. Utiliser plusieurs grilles multiplie simplement les chances de gagner.
Conditions de gain :
- Il y a gain sur une grille selon le nombre de numéros corrects, y compris le numéro complémentaire.
- Les montants des gains pour une grille simple sont donnés par le tableau suivant :
| Combinaison | Gain (G) | probabilité (p) |
|---|---|---|
| 5 + Chance | Jackpot (2 000 000) | 1/19 068 840 |
| 5 | 200 000 | 1/1 906 884 |
| 4 + Chance | 800 | 1/86 676,55 |
| 4 | 300 | 1/8 667,655 |
| 3 + Chance | 40 | 1/2 015,73 |
| 3 | 20 | 1/201,573 |
| 2 + Chance | 7 | 1/143,98 |
| 2 | 4 | 1/14,398 |
| 1 + Chance | 2,20 | 1/28,09 |
| 1 | 0 | 1/2,809 |
| 0 + Chance | 2,20 | 1/17,56 |
| 0 | 0 | 1/1,756 |
A noter dans ce tableau :
1. Le gain (G) est le gain en euros, versé par la FDJ par grille standard pour un coût de participation c = 2,20 euros, correspondant au barème officiel de la FDJ, variable selon le tirage. Les valeurs de G indiquées dans le tableau sont un exemple illustratif mais plausible.
2. La probabilité (p) est la probabilité qu'une combinaison donnée aboutisse au gain G. Elle se calcule comme suit, avec n = nombre de numéros gagnants :
p(n) = C(5, n) C(44, 5 - n) / C(49, 5) et p(n + Chance) = p(n) x 1/10 avec :
Coefficient binomial C(a, b) = a! / (b! (a - b)!)
C(5, n) : nombre de façons de choisir les n numéros gagnants parmi les 5 tirés
C(44, 5 - n) : nombre de façons de choisir les (5 - n) numéros perdants parmi les 44 non tirés.
C(49, 5)
: nombre total de combinaisons possibles de 5 numéros parmi 49
3. L'espérance mathématique (E) de la grille est la différence entre le gain espéré ∑i [Gi x pi] et le coût c, soit : Egrille = -1,297 euros
En moyenne, sur chaque grille simple, le joueur perd donc environ 1,30 euros sur un coût de 2,20 euros, soit près de 60 % du montant misé.
Déroulement du tirage :
- Les dates officielles des tirages sont : lundi, mercredi et samedi soir.
- Le tirage est diffusé en direct ou sur plateformes officielles.
-
Les 5 numéros principaux et le complémentaire sont tirés de manière continue.
-
Les résultats sont vérifiés individuellement après le tirage.
-
Les gains sont attribués automatiquement selon les règles officielles.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au loto FDJ car le hasard intervient à deux niveaux :
- celui des numéros gagnants. Toutes les grilles sont équiprobables avec une probabilité fixe indépendante du choix du joueur.
- celui des gains qui sont variables avec le nombre de joueurs. Le Jackpot (5 numéros + Chance) et le "5 numéros" sont partagés entre gagnants.
Mais il existe une stratégie rationnelle de gestion du risque, basée sur les règles suivantes [PER][CHA] :
1. Définir un budget par tirage : par exemple 5 à 10 grilles maximum, pour un coût entre 11 et 22 euros.
2. Respecter strictement votre budget : le loto FDJ demeure un divertissement coûteux, avec une perte statistique moyenne de 1,30 euros par grille, soit près de 60 % du coût.
3. Répartir le jeu dans le temps, non pour augmenter l'espérance de gain (qui reste négative), mais pour limiter l'impact psychologique des pertes ponctuelles.
4. Varier les grilles (choix personnels et FLASH) afin de diversifier les combinaisons et de rendre le jeu plus ludique.
B7.6.2. La roulette [PER][CHA] :
La roulette est un jeu de hasard à plusieurs joueurs indépendants, admettant une dimension stratégique très limitée.
Elle se joue généralement de 1 à 9 joueurs, selon la taille du tapis de jeu.
Matériel :
1. Une roue de roulette (ou "cylindre") : roue circulaire compartimentée en cases numérotées et colorées, montée sur un axe permettant une rotation libre.
La roue peut être européenne ou française (37 cases avec un seul zéro), ou américaine (38 cases avec deux zéros).
2. Une bille : petite sphère destinée à circuler dans la roue et à se fixer dans l'une des cases lors de l'arrêt de la roue.
3.
Un tapis (ou table) de jeu : surface plane portant les numéros et types de mises possibles, sur laquelle les joueurs placent leurs mises.
4. Les jetons : unités utilisées par les joueurs pour matérialiser leurs mises.
Disposition des numéros sur la roue :
En roulette européenne, française et américaine, l'ordre exact des numéros sur la roue, en commençant par le zéro et en allant dans le sens des aiguilles d'une montre, est historique et ne suit aucune règle mathématique simple. Cet ordre est le suivant (voir Figures ci-dessus [BLE][GUI1][GUI2]) :
- Roulette européenne et française (37 cases avec un seul zéro) : 0, 32, 15, 19, 4, 21, 2, 25, 17, 34, 6, 27, 13, 36, 11, 30, 8, 23, 10, 5, 24, 16, 33, 1, 20, 14, 31, 9, 22, 18, 29, 7, 28, 12, 35, 3, 26
- Roulette américaine (38 cases avec 0 et 00) : 0, 28, 9, 26, 30, 11, 7, 20, 32, 17, 5, 22, 34, 15, 3, 24, 36, 13, 1, 00, 27, 10, 25, 29, 12, 8, 19, 31, 18, 6, 21, 33, 16, 4, 23, 35, 14, 2
L'ordre des numéros sur la roue est conçu pour obtenir un équilibre optimal et garantir l'équité du jeu. Si l'on sépare la roue en deux au niveau du zéro :
- Chaque moitié contient exactement le même nombre de rouges et noirs
- Chaque moitié contient exactement le même nombre de pairs et impairs
- Chaque moitié contient exactement le même nombre de manque (1-18) et passe (19-36)
-
Chaque moitié contient exactement une moitié de chaque douzaine.
-
Chaque moitié contient exactement une moitié de chaque colonne.
Les numéros 0 et 00 sont verts. Les numéros 1 à 36 comprennent 18 rouges et 18 noirs, disposés en alternance stricte rouge/noir autour de la roue, sans aucun doublon de couleur.
Pour ces trois variantes de roulette, la couleur des numéros de 1 à 36 peut être mémorisée simplement comme suit : les numéros dont la somme des chiffres est impaire sont rouges, ceux dont la somme est paire sont noirs. Cette règle admet deux exceptions : les numéros 10 et 28, qui sont noirs.
La disposition des numéros sur la roue a toutefois peu d'importance d'un point de vue probabiliste, tant que la roulette est mécaniquement parfaite et non usée, c'est-à-dire sans défauts minimes d'équilibrage ou de rugosité favorisant une portion de la roue. Historiquement, cette disposition pouvait légèrement atténuer les biais mécaniques locaux [TOU], mais aujourd'hui, avec des roues parfaitement équilibrées et un contrôle statistique rigoureux par les casinos, cet effet est devenu pratiquement nul.
Déroulement d'un tour :
Le but du jeu est de prédire correctement la case ou la couleur où la bille va s'arrêter.
Un tour typique se déroule ainsi :
-
Le croupier fait tourner la roue et lance la bille en sens inverse.
-
Les joueurs placent leurs mises sur le tapis avant que la bille ne s'immobilise.
-
La bille s'arrête dans une case.
- Les gains sont payés en fonction des mises.
Le croupier [WIK10] :
Le croupier est un employé du casino. Il manipule la bille et la roue, enregistre les mises, règle les gains des joueurs et annonce les phases de jeu à l'aide de formules consacrées :
- "Faites vos jeux" : début de la période de mises.
- "Les jeux sont faits" : lancement de la bille. Aucune nouvelle mise n'est acceptée.
- "Rien ne va plus" : confirmation de la clôture des mises. L'issue du coup est imminente.imminent.
- "4 rouge pair et manque" (exemple) : annonce du numéro gagnant et de ses caractéristiques (couleur, parité, plage).
- "Rien au numéro" : aucun joueur n'a gagné sur une mise en Plein.
- "Rien ne va" : la bille est sortie accidentellement de la roue avant de s'immobiliser. Le coup est annulé et rejoué.
Types de mise :
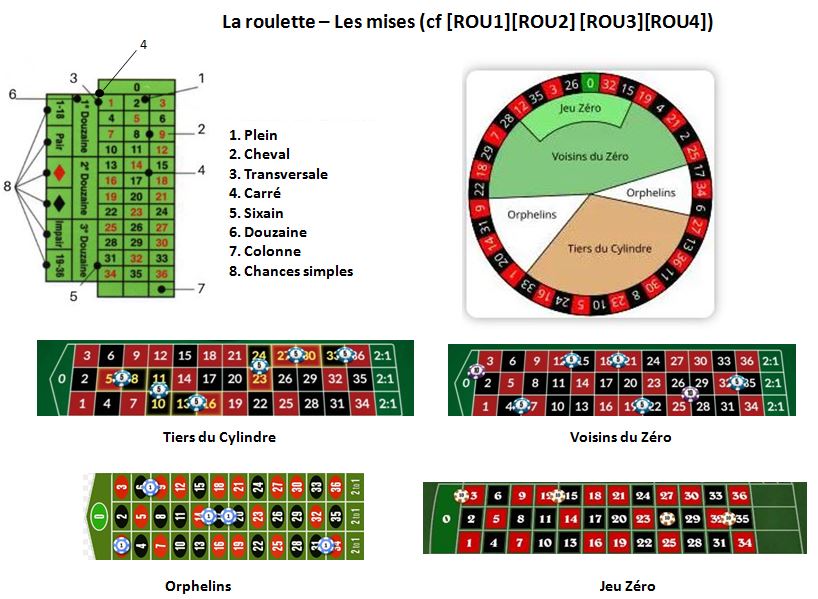
On peut classer les mises en trois grandes catégories selon l'emplacement de la mise sur le tapis :
- Mises internes (voir Figure 1 ci-dessus, repères 1 à 5) : mises placées directement sur un ou plusieurs numéros de la grille, couvrant des numéros précis (Plein, Cheval, Transversale, Carré, Sixain).
-
Mises externes simples (voir Figure 1 ci-dessus, repères 6 à 8) : mises placées à l'extérieur de la grille, portant sur des caractéristiques ou groupes de numéros (couleur, parité, Manque/Passe, Douzaine, Colonne).
-
Mises externes spéciales (voir Figure 2 ci-dessus) : mises annoncées par le joueur et constituées de plusieurs mises internes réparties par le croupier sur le tapis, couvrant un secteur particulier de la roue (Tiers du Cylindre, Voisins du Zéro, Orphelins, Jeu Zéro).
Le tableau suivant couvre tous les types de mise classiques en roulette européenne (EU), française (FR) et américaine (US) [WIK10] :
| Type de mise | Nom | Description | EU/FR/US : Gain (G) | EU/FR : probabilité (p) | EU/FR : Espérance (E) | US : probabilité (p) | US : Espérance (E) | Type de Chance |
|---|---|---|---|---|---|---|---|---|
| Mises internes | Plein (ou Straight Up) | Mise sur un seul numéro | 36 | 1/37 | -1/37 | 1/38 | -2/38 | Chance multiple |
| Cheval (ou Split) | Mise sur 2 numéros adjacents | 18 | 2/37 | -1/37 | 2/38 | -2/38 | Chance multiple | |
| Transversale (ou Street) | Mise sur une rangée de 3 numéros | 12 | 3/37 | -1/37 | 3/38 | -2/38 | Chance multiple | |
| Carré (ou Corner) | Mise sur 4 numéros formant un carré | 9 | 4/37 | -1/37 | 4/38 | -2/38 | Chance multiple | |
| Carré "Quatre Premiers" | Mise sur 4 numéros 0-1-2-3 | EU/FR : 9 | 4/37 | -1/37 | N/A | N/A | Chance multiple | |
| Sixain (ou Six Line) | Mise sur deux rangées adjacentes (6 numéros) | 6 | 6/37 | -1/37 | 6/38 | -2/38 | Chance multiple | |
| Cinq numéros (ou Five Number Bet) | Mise sur 5 numéros 0-00-1-2-3 | US : 7 | N/A | N/A | 5/38 | -3/38 | Chance multiple | |
| Mises externes simples | Rouge/Noir (ou Red/Black) | Pari sur la couleur de la case | 2 | 18/37 | -1/37 ou FR : -1/74 (La Partage ou En prison) | 18/38 | -2/38 | Chance simple |
| Pair/Impair (ou Even/Odd) | Pari sur la parité du numéro | 2 | 18/37 | -1/37 ou FR : -1/74 (La Partage ou En prison) | 18/38 | -2/38 | Chance simple | |
| Manque/Passe (ou Low/High) | Pari sur les numéros 1-18 (Manque) ou 19-36 (Passe) | 2 | 18/37 | -1/37 ou FR : -1/74 (La Partage ou En prison) | 18/38 | -2/38 | Chance simple | |
| Douzaine (ou Dozen) | Pari sur 12 numéros consécutifs (Premiers : 1-12, Moyens : 13-24, Derniers : 25-36) | 3 | 12/37 | -1/37 | 12/38 | -2/38 | Chance multiple | |
| Colonne (ou Column) | Pari sur une des trois colonnes verticales du tapis (12 numéros) | 3 | 12/37 | -1/37 | 12/38 | -2/38 | Chance multiple | |
| Mises externes spéciales | Tiers du Cylindre | Mise couvrant 12 numéros opposés au 0 (6 jetons) | EU/FR : Variable selon le numéro sorti (mise composée) | Proportion de numéros couverts sur la roue | -1/37 | N/A | N/A | Chance multiple |
| Voisins du Zéro | Mise couvrant 17 numéros autour du 0 (9 jetons) | EU/FR : Variable selon le numéro sorti (mise composée) | Proportion de numéros couverts sur la roue | -1/37 | N/A | N/A | Chance multiple | |
| Orphelins | Mise couvrant 8 numéros non couverts par Tiers du Cylindre et Voisins (5 jetons) | EU/FR : Variable selon le numéro sorti (mise composée) | Proportion de numéros couverts sur la roue | -1/37 | N/A | N/A | Chance multiple | |
| Jeu Zéro | Mise couvrant 7 numéros autour du 0 (4 jetons) | EU/FR : Variable selon le numéro sorti (mise composée) | Proportion de numéros couverts sur la roue | -1/37 | N/A | N/A | Chance multiple |
A noter dans ce tableau :
1. Le gain (G) est le gain total en jetons (mise comprise), versé par le casino pour 1 jeton misé (coût c = 1), lorsque la mise est gagnante. Par exemple, si le joueur mise 1 jeton sur un numéro Plein gagnant, il récupère 35 + 1 soit 36 jetons.
2. La probabilité (p) est la probabilité qu'un tour de roulette aboutisse à un gain total G pour un jeton misé.
- Pour les mises à gain fixe (Plein, Chance simple, Douzaine, etc.), p est la probabilité physique que l'événement gagnant se produise.
- Pour les mises composées ou les règles spéciales ("La Partage", "En Prison"), p peut être une probabilité effective, intégrant des gains partiels,
des neutralisations (zéro)
ou des tours conditionnels.
3. L'espérance mathématique (E) est la différence entre le gain espéré (G x p) et le coût c, soit : E = (G x p) - c
En roulette européenne et française, et hors règles spéciales "Le Partage" et "En Prison" (voir ci-dessous), on trouve : E = -1/37 = -0,027, soit une perte moyenne de 2,7 % par mise, quelle que soit le type de mise (interne ou externe).
4. L'indication N/A signifie : Non Applicable.
5. Bien que l'espérance soit identique pour toutes les mises, distinguer Chances simples et Chances multiples est important pour le joueur car :
- Les Chances simples sont des mises à gain faible et forte probabilité, donc offrant des gains moins spectaculaires mais plus fréquents, idéales pour un joueur prudent.
- Les Chances multiples sont des mises à gain élevé et faible probabilité, donc offrant des gains plus volatils, adaptées à un joueur audacieux.
6. Pour les mises externes spéciales, la disposition des jetons sur la grille est la suivante ;
Attention : dans certaines impressions sur roue de fabricant ainsi que dans des photos d'articles, le numéro 27 est classé à tort parmi les Orphelins alors qu'il appartient au Tiers du Cylindre.
- Tiers du Cylindre (6 jetons pour 12 numéros, voir Figure 3 ci-dessus) : 6 jetons, un sur chaque Cheval (5/8, 10/11, 13/16, 23/24, 27/30, 33/36)
- Voisins du Zéro (9 jetons pour 17 numéros, voir Figure 4 ci-dessus) : 1 jeton sur le zéro + 8 jetons, un sur chaque Cheval (4/7, 12/15, 18/21, 19/22, 32/35), deux sur Transversale (0-2-3), deux sur Carré (25-26-28-29)
- Orphelins (5 jetons pour 8 numéros, voir Figure 5 ci-dessus) : 1 jeton sur le numéro 1 + 4 jetons, un sur chaque Cheval (6/9, 14/17, 17/20, 31/34)
- Jeu Zéro (4 jetons pour 7 numéros, voir Figure 6 ci-dessus) : 1 jeton sur le numéro 26 + 3 jetons, un sur chaque Cheval (0/3, 12/15, 32/35)
7. La roulette américaine standard diffère de la roulette européenne et française par des probabilités légèrement plus faibles (donnant E = -2/38) et l'ajout d'une mise spéciale : la mise de Cinq numéros 0-00-1-2-3 (donnant E = -3/38). L'espérance E passe de -2,7 % à respectivement -5,26 % et -7,89 %, nettement moins favorable pour le joueur.
8. Les limites de mise, variables selon le type de mise et la variante de roulette, s'étendent typiquement de 1 à 1000 euros pour les Chances simples (afin de satisfaire la majorité des joueurs) et de 1 à 100 euros pour les Chances multiples (afin de protéger la trésorerie du casino en cas de gains ponctuels très élevés).
Les numéros verts :
Lorsque la bille tombe sur un numéro vert (0, et 00 pour la roulette américaine), toutes les mises couvrant le 0 sont gagnantes (Plein 0, Chevaux 0-1, 0-2 et 0-3, Carré 0-1-2-3, Cinq numéros US, Voisins du Zéro, Jeu Zéro).
Toutes les autres mises sont perdantes, à l'exception des Chances simples en roulette française lorsqu'elles bénéficient des règles spéciales suivantes :
La Partage, où le joueur récupère la moitié de sa mise, ce qui conduit à une espérance E = -1/74 = -1,35 %
Démonstration : Sur cas non-zéro, le casino verse au joueur (mise comprise) G = 2 avec probabilité 18/37. Sur cas zéro, le casino verse G = 0,5 avec probabilité 1/37. D'où E = ∑[Gi x pi] - c = 36/37 + 0,5/37 - 1 = -1/74
En Prison, où la mise est conservée pour le coup suivant et n'est perdue que si ce second tirage est défavorable, ce qui conduit à une espérance par mise E = -1/74 = -1,35 %
Démonstration : Sur cas non-zéro, le casino verse au joueur (mise comprise) G = 2 avec probabilité 18/37. Sur cas zéro, et en supposant que le zéro ne sorte pas deux fois de suite, le casino verse G avec probabilité 1/37, G valant 1 avec probabilité 18/36 si succès du joueur au second tour. D'où l'espérance E par mise = ∑[Gi x pi] - c = 36/37 + 1/74 - 1 = -1/74
Attention : Certains articles aboutissent au résultat erroné E = -1/73. L'erreur vient de l'exclusion arbitraire d'un cas sur 74, celui du cas zéro + succès (probabilité (1/37)(18/36) avec G = 1), résultant d'une confusion entre "gain net = 0" (qui est correct) et "paiement réel G = 1" (qui est exclu à tort comme "ne comptant pas" [DEL2]). D'où le calcul biaisé : E = 72/73 + 0 - 1 = -1/73 au lieu du calcul correct : E = 72/74 + 1/74 - 1 = -1/74
Calcul général pour m cas zéro successifs ( m ≥ 1) :
On note : a = 1/37
1. Cas non-zéro (au premier tour) : le casino verse au joueur (mise comprise) G = 2 avec probabilité 18/37, soit une contribution : 36 a
2. Cas zéros successifs : Si le zéro sort k fois de suite (avec k < m), alors le casino verse G avec probabilité ak, G valant 1 avec probabilité 18 a si succès du joueur au tour suivant, soit une contribution : ak 18 a = 18 ak + 1, pour k = 1, 2,..., m - 1
3. Cas du dernier zéro sans suite : Au m ième zéro, le casino verse G avec probabilité am, G valant 1 avec probabilité 18/36 = 1/2 si succès conditionnel du joueur au tour suivant (zéro exclu), soit une contribution : (1/2) am
L'espérance E pour une mise de 1 (coût c = 1) est donc la suivante :
E = 36 a + 18 a2 + 18 a3 + ... + 18 am + (1/2) am - c
En posant : A = 1 + a + ... + am - 2 = (1 - am - 1)/(1 - a) = (1 - am - 1)/(36 a), E s'écrit alors :
E = 36 a + B - 1
avec : B = 18 a2 A + (1/2) am = 18 a2 (1 - am - 1)/(36 a) + (1/2) am = a/2
On obtient finalement : E = 36 a + a/2 - 1 = 73 a/2 - 1 = -1/74
Conclusion : Quel que soit le nombre m de zéros successifs envisagés dans le mode En prison, l'espérance mathématique d'une mise unitaire reste exactement égale à E = -1/74, sans aucune approximation.
Dans ces deux règles particulières, les Chances simples ne sont pas perdues intégralement ou fatalement. Le joueur est ainsi avantagé car l'espérance passe de -2,7 % à -1,35 % avec la règle La partage ou En prison.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante à la roulette. Mais il existe une stratégie optimale visant à limiter les pertes et gérer le risque, basée sur les règles suivantes [PER][CHA] :
1. Limiter le nombre de coups : La roulette étant un jeu de hasard avec espérance négative, plus on joue longtemps, plus la perte moyenne converge vers l'espérance théorique (-2,7 % en roulette européenne et française).
Jouer moins de coups réduit la probabilité d'atteindre des pertes importantes.
2. Privilégier les Chances simples (Rouge/Noir, Pair/Impair, Manque/Passe) : Toutes les mises ont la même espérance négative de gain par coup (-2,7 %), mais les Chances simples offrent des gains moins spectaculaires mais plus fréquents, évitant les pertes brutales. Par ailleurs, à la roulette française, cette espérance négative est réduite à -1,35 % par mise avec la règle La Partage ou En Prison.
3. Jouer les numéros dits "fréquents" est une illusion, non pas en raison de la disposition des numéros sur le tapis, mais parce qu'un défaut mécanique sur une case précise de la roue est extrêmement improbable pour deux raisons principales :
- Une roulette usée ou défectueuse favorise une zone géographique de la roue (secteur contigu), non une case isolée.
- Les casinos contrôlent, ajustent et remplacent les roues dès qu'une anomalie statistique apparaît.
4. Une stratégie rationnelle à la roulette consiste à fixer un capital initial et un seuil d'arrêt, par exemple -30 %, le joueur assumant psychologiquement une éventuelle perte totale de ses gains. Elle ne modifie pas l'espérance négative du jeu, mais permet de jouer sereinement et longtemps, tout en limitant les pertes avant qu'elles ne s'aggravent.
B7.6.3. La boule [PER][CHA] :
La Boule est une variante simplifiée de la roulette, utilisant uniquement les chiffres de 1 à 9.
Elle se joue généralement de 1 à 8 joueurs, selon la taille du tapis de jeu.
Matériel :
1. Un roue de jeu : cylindre circulaire compartimenté en cases numérotées de 1 à 9 et colorées, montée sur un axe permettant une rotation libre.
2.
Une boule : petite sphère destinée à circuler dans la roue et à se fixer dans l'une des cases lors de l'arrêt de la roue. La boule est une bille un peu plus grosse que celle de la roulette afin de s'adapter aux cases plus grandes.
3.
Un tapis (ou table) de jeu : surface plane portant les numéros et les types de mises possibles, sur laquelle les joueurs placent leurs mises.
4.
Les jetons : unités utilisées par les joueurs pour matérialiser leurs mises.
Disposition des numéros sur la roue :
En casino, la Boule se joue principalement sur une roue à 18 cases (avec deux séries successives de 1 à 9).
Les autres versions (comme 27 cases) existent mais sont rares et hors du cadre standard.
L'ordre exact des numéros sur la roue, en commençant par le 1 et en allant dans le sens des aiguilles d'une montre, suit un ordre linéaire 1-2-3-4-5-6-7-8-9 (première séquence) suivi d'une seconde séquence identique (voir Figure ci-dessus [BON]) :
Le numéro 1 est noir. Les numéros rouge et noir alternent ensuite sur la roue, en sautant le numéro 5 qui est vert.
Déroulement d'un tour :
Le déroulement d'un tour est identique à celui de la roulette.
Le croupier :
Le rôle du croupier au jeu de Boule en version "roue tournante" est identique à celui de la roulette en remplaçant le mot "bille" par "boule".
Types de mise :
On peut classer les mises en deux grandes catégories selon l'emplacement de la mise sur le tapis (voir Figure ci-dessus) :
- Mises internes : mises placées directement sur un ou plusieurs numéros de la grille, couvrant des numéros précis (Plein).
-
Mises externes : mises placées à l'extérieur de la grille, portant sur des caractéristiques ou groupes de numéros (couleur, parité, Manque/Passe).
Le tableau suivant couvre tous les types de mise classiques :
| Type de mise | Nom | Description | Gain (G) | probabilité (p) | Espérance (E) | Type de Chance |
|---|---|---|---|---|---|---|
| Mises internes | Plein (ou Straight Up) | Mise sur un seul numéro | 8 | 1/9 | -1/9 | Chance multiple |
| Mises externes | Rouge/Noir (ou Red/Black) | Pari sur la couleur de la case | 2 | 4/9 | -1/9 | Chance simple |
| Pair/Impair (ou Even/Odd) | Pari sur la parité du numéro | 2 | 4/9 | -1/9 | Chance simple | |
| Manque/Passe (ou Low/High) | Pari sur les numéros 1-4 (Manque) ou 6-9 (Passe) | 2 | 4/9 | -1/9 | Chance simple |
A noter dans ce tableau :
1. Le gain (G) est le gain total en jetons (mise comprise), versé par le casino pour 1 jeton misé (coût c = 1), lorsque la mise est gagnante. Par exemple, si le joueur mise 1 jeton sur un numéro Plein gagnant, il récupère 7 + 1 soit 8 jetons.
2. La probabilité (p) est la probabilité physique qu'un tour de jeu aboutisse à un gain total G pour un jeton misé.
3. L'espérance mathématique (E) est la différence entre le gain espéré (G x p) et le coût c, soit : E = (G x p) - c.
On trouve donc : E = -1/9 = -0,111, soit une perte moyenne de 11,1 % par mise, quelle que soit le type de mise (interne ou externe).
4. Bien que l'espérance soit identique pour toutes les mises, distinguer Chances simples et Chances multiples est important pour le joueur car :
- Les Chances simples sont des mises à gain faible et forte probabilité, donc offrant des gains moins spectaculaires mais plus fréquents, idéales pour un joueur prudent.
- Les Chances multiples sont des mises à gain élevé et faible probabilité, donc offrant des gains plus volatils, adaptées à un joueur audacieux.
Le numéro vert :
Lorsque la bille tombe sur le numéro vert (5), seule la mise Plein 5 est gagnante et toutes les autres mises (Plein 1-4 et 6-9, et Chances simples) sont perdantes.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante à la Boule. Mais il existe une stratégie optimale visant à limiter les pertes et gérer le risque.
Cette stratégie est identique à celle de la roulette mais avec une espérance négative nettement plus élevée (environ -11 % contre -2,7 %).
En contrepartie, la Boule est un jeu plus simple, offrant des parties rapides et intuitives.
B7.6.4. Les machines à sous [PER][CHA] :

Les machines à sous sont des jeux de hasard individuels, admettant une dimension stratégique très limitée.
On distingue principalement trois catégories de machines :
- les machines mécaniques classiques à trois rouleaux.
- les machines vidéo modernes avec écran numérique et rouleaux virtuels, souvent au nombre de cinq.
- les machines progressives, dont une partie des mises alimente un pot collectif partagé entre plusieurs machines connectées.
Sont décrites ci-dessous les règles de jeu de la machine classique à trois rouleaux.
Matériel (voir Figure ci-dessus):
1. Une machine constituée de trois rouleaux mécaniques disposé l'un contre l'autre. Chaque rouleau porte un nombre déterminé de symboles distincts répartis sur sa circonférence. Une "ligne de paiement" horizontale traverse les rouleaux. Les symboles qui s'y alignent à l'arrêt déterminent si la combinaison est gagnante et le montant du gain associé.
2. Les jetons (ou pièces) : unités utilisées par les joueurs pour participer au jeu.
3. Le levier ou bouton de mise en jeu : mécanisme actionné par le joueur pour déclencher la rotation simultanée des trois rouleaux.
Disposition des symboles sur le rouleau :
Chaque rouleau est un cylindre comportant un nombre déterminé de positions successives (généralement 64), chacune marquée d'un symbole standard.
Les symboles les plus courants sont les suivants :
- Cerise : symbole fréquent, gain modeste.
- Bar (BAR) : symbole moins fréquent, gains plus élevés.
- Etoile ou Cloche : symboles rares, gains substantiels.
- Chiffre 7 : symbole très rare, souvent associé au gain maximal (jackpot).
- Symbole sans valeur de gain (généralement : blanc).
La fréquence d'apparition de chaque symbole, ainsi que la table de paiements associée aux différentes combinaisons gagnantes, sont définies par le fabricant de la machine, de manière à assurer un avantage mathématique pour la maison (casino), généralement compris entre 5 % et 10 % des mises engagées.
Déroulement d'un coup de jeu :
- Mise : Le joueur insère 1, 2 ou 3 jetons. 3 jetons sont requis pour accéder au jackpot.
- Lancement : Le joueur actionne le levier ou le bouton, faisant tourner simultanément les trois rouleaux.
- Arrêt : Les rouleaux s'arrêtent successivement. Les gains sont attribués uniquement lorsque les trois symboles alignés sur la ligne de paiement centrale sont rigoureusement identiques. Sinon, le coup est perdu.
- Fin : La mise engagée par le joueur est définitivement consommée. Lorsque la combinaison obtenue est gagnante, la machine délivre un nombre de jetons correspondant au gain prévu par la table de paiements.
Conditions de gain :
- Le montant du gain dépend de la combinaison obtenue et du nombre de jetons misés (1, 2 ou 3), selon la table de paiements.
- La table de paiements indique les gains en jetons, versés par la machine pour 1 jeton misé et consommé.
- Sur une machine classique à trois rouleaux, chaque rouleau comportant 64 symboles, les montants des gains par combinaison sont donnés par le tableau suivant :
| Combinaison | Nombre de symboles par rouleau | Gain (G) | probabilité (p) |
|---|---|---|---|
| une cerise | c = 16 | 0 | 3 × (c/64) × ((64 - c)/64)2 = 0,422 |
| deux cerises | c = 16 | 0 | 3 × (c/64)2 × (64 - c)/64 = 0,0469 |
| trois cerises | c = 16 | 10 | (c/64)3 = 0,0156 |
| trois Bar | b = 8 | 120 | (b/64)3 = 1,95 10 -3 |
| trois Etoile ou Cloche | e = 4 | 250 | (e/64)3 = 2,44 10 -4 |
| trois 7 | s = 1 | 800 (Jackpot) | (s/64)3 = 3,81 10-6 |
A noter dans ce tableau :
1. Le gain (G) est le gain en jetons, versé par la machine pour 1 jeton misé et consommé (coût c = 1), selon le tableau des paiements. Les valeurs de G indiquées dans le tableau sont un exemple illustratif mais plausible pour une machine classique.
2. La probabilité (p) est la probabilité qu'une combinaison donnée aboutisse au gain G.
Pour exemple, le calcul de p pour la combinaison "Une cerise" est le suivant :
3 = trois positions possibles pour la cerise sur la ligne de paiement (gauche, centre ou droite).
(c/64) = probabilité d'avoir 1 cerise sur la position donnée.
((64 - c)/64)2 = probabilité que les 2 autres symboles soient n'importe quoi sauf cerise.
3. L'espérance mathématique (E) d'un coup est la différence entre le gain espéré ∑i [Gi x pi] et le coût c, soit : Ecoup = -0,055
En moyenne, sur chaque coup de jeu, le joueur perd donc environ 5,5 % de sa mise initiale.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante sur une machine à sous, car chaque coup est indépendant et régi par le hasard.
Mais il existe une stratégie optimale visant à limiter les pertes et gérer le risque.
Cette stratégie est identique à celle de la roulette mais avec une espérance négative nettement plus élevée (environ -5,5 % contre -2,7 %).
B7.7. Jeux de pari sportif :
B7.7.1. Le PMU français [PER][CHA] :
Le PMU français (Pari Mutuel Urbain) est un jeu de pari hippique, opposant plusieurs joueurs indépendants misant sur un même événement.
Ce jeu n'admet qu'une dimension stratégique limitée, le comportement des chevaux demeurant prépondérants.
Matériel :
1. Liste officielle des partants, publiée avant chaque course, permettant au joueur de connaître les numéros, noms, jockeys (ou drivers) et cotes indicatives des chevaux engagés.
2. Grille de jeu mentionnant dans l'ordre standardisé (voir Figure ci-dessus) :
- l'identification de la course dans l'en-tête de la grille : numéro de réunion (correspondant à l'hippodrome avec date/heure) et numéro de la course
- le type de pari, sélectionné au moyen de boutons ou de cases
- le mode ordre/désordre, à cocher dans des cases spécifiques
- les numéros des chevaux choisis par grille principale : cases numérotées 1 à 18
- la mise engagée : montant unitaire (1.50, 2, 3 euros, etc.) ou multiples
Exemple de grille Quinté+ ordre : [Réunion 1 - R5 Vincennes], [Quinté+], [Ordre], [Numéros cochés : 2-8-11-14-6], [Mise : 2 euros].
3. Type de support de jeu : soit bulletin papier (rempli manuellement et validé à un guichet de point de vente agrée), soit enregistrement numérique réalisé via un terminal électronique en point de vente (exemple : bureaux de tabac partenaires), soit application mobile ou site officiel du PMU (pmu.fr)
Déroulement d'une course :
- Début : La course débute par la présentation des chevaux au public et au rond de présentation (environ 30 minutes avant le départ). Les prises de paris demeurent ouvertes jusqu'à leur fermeture officielle, généralement 2 à 5 minutes avant le départ effectif.
- Course : L'épreuve, d'une durée moyenne comprise entre 1 et 5 minutes (courses de plat, de trot ou d'obstacles), se déroule sous le contrôle des officiels et des commissaires chargés de veiller au respect du code des courses. A l'arrivée, un classement provisoire est établi. En cas d'arrivée serrée, le recours à la photo-finish permet de déterminer l'ordre d'arrivée.
- Résultats définitifs : Les résultats deviennent définitifs après validation par les commissaires, en principe dans un délai de 10 à 20 minutes suivant l'arrivée, sauf réclamation ou enquête.
Cette validation entraîne la publication officielle des rapports et déclenche le règlement des gains aux parieurs gagnants.
Conditions de gain :
Le montant de gains est proportionnel à la mise engagée et inversement proportionnel au montant total des mises gagnantes enregistrées sur le même pari.
Pour chaque type de pari et pour chaque course, les mises des parieurs constituent une masse commune (appelée "pool"). Après application des prélèvements réglementaires (généralement 20 %), le solde est réparti entre les seuls parieurs gagnants, au prorata de leur mise.
Exemple :
- Pool total de 100 euros.
- Somme des mises à répartir R = 80 euros (après application d'un prélèvement de 20 %).
- S'il y a 2 seuls gagnants ayant misé respectivement 1 euro et 3 euros, alors le rapport r (ou "cote") est le rapport entre la somme R des mises à répartir et la somme des mises gagnantes soit r = 80/(1 + 3) = 20
- Chaque gagnant reçoit alors un montant égal à mise x rapport, soit 20 euros pour le premier joueur et 60 euros pour le second.
- Le gain réel de chaque joueur, après déduction de la mise initialement engagée, est donc respectivement de 19 euros et 57 euros.
Le tableau suivant donne les principaux types de pari proposés par le PMU, avec leur probabilité théorique de gain (calculée sur une course à n = 15 chevaux partants).
| Type de pari | Description | rapport moyen (r) | probabilité (p) | Espérance (E) |
|---|---|---|---|---|
| Simple gagnant | 1er exact | 6-12 | 1/n = 1/15 = 6.67 % | -0.60 à -0.20 |
| Simple placé | 1er, 2e ou 3e | 1-3 | 3/n (pour n ≥ 8) = 3/15 = 20.0 % | -0.80 à -0.40 |
| Couplé ordre | 1er et 2e dans l'ordre | 80-200 | 1/(n(n - 1)) = 1/210 = 0.476 % | -0.62 à -0.05 |
| Couplé désordre | 1er et 2e dans le désordre | 25-60 | C(n - 2, 0)/C(n, 2) = 2/(n(n - 1)) = 2/210 = 0.952 % | -0.76 à -0.43 |
| 2 sur 4 | Choix de 4 chevaux dont 2 au moins terminent parmi les 4 premiers | 3-15 | C(n - 2, 2)/C(n, 4) = 78/1365 = 5.71 % | -0.83 à -0.14 |
| Trio ordre | 1er, 2e et 3e dans l'ordre | 800-1200 | 1/(n(n - 1)(n - 2)) = 1/2730 = 0.0366 % | -0.71 à -0.56 |
| Trio désordre | 1er, 2e et 3e dans le désordre | 25-40 | C(n - 3, 0)/C(n, 3) = 6/(n(n - 1)(n - 2)) = 6/2730 = 0.220 % | -0.95 à -0.91 |
| Tiercé ordre | 1er, 2e et 3e dans l'ordre, avec report possible | 800-2500 (hors bonus B) 50-200 (avec B moyen = 0.08 %) | 1/(n(n - 1)(n - 2)) = 1/2730 = 0.0366 % + B moyen = 0.12 % | -0.71 à -0.084 -0.067 à +1.92 |
| Tiercé désordre | 1er, 2e et 3e dans le désordre, avec report possible | 80-300 (hors bonus B ou avec B moyen = 0.25 %) | C(n - 3, 0)/C(n, 3) = 3!/(n(n - 1)(n - 2)) = 6/2730 = 0.220 % + B moyen = 0.47 % | -0.82 à -0.34 -0.62 à +0.41 |
| Quarté+ ordre | 1er à 4e dans l'ordre exact, avec report possible | 10000-80000 (hors bonus B ou avec B moyen = 0.15 %) | 1/(n(n - 1)(n - 2)(n - 3)) = 1/32760 = 0.00305 % + B moyen = 0.153 % | -0.70 à +1.4 +14.3 à +121.4 |
| Quarté+ désordre | 1er à 4e dans le désordre, avec report possible | 1000-15000 (hors bonus B ou avec B moyen = 0.30 %) | C(n - 4, 0)/C(n, 4) = 4!/(n(n - 1)(n - 2)(n - 3)) = 24/32760 = 0.0732 % + B moyen = 0.301 % | -0.27 à +10.0 +2.0 à +44.2 |
| Quinté+ ordre | 1er à 5e dans l'ordre exact | 80000-300000 | 1/(n(n - 1)(n - 2)(n - 3)(n - 4)) = 1/360360 = 0.00028 % | -0.78 à -0.16 |
| Quinté+ désordre | 1er à 5e dans le désordre, avec report possible | 2500-25000 (hors bonus B ou avec B moyen = 0.11 %) | C(n - 5, 0)/C(n, 5) = 5!/(n(n - 1)(n - 2)(n - 3)(n - 4)) = 120/360360 = 0.0333 % + B moyen = 0.143 % | -0.17 à +7.3 +2.6 à +34.8 |
| Tic 3 | Choix de 5 chevaux permettant de jouer conjointement au Tiercé, Quarté+ et Quinté+ dans le désordre | 15-80 | C(5, 3)/C(n, 3) + C(5, 4)/C(n, 4) + C(5, 5)/C(n, 5) = 10/455 + 5/1365 + 1/3003 = 2.60 % | -0.61 à +1.08 |
A noter dans ce tableau :
1. Le rapport (r) est le rapport final (euros gagnés par euro misé), publié après course.
2. La probabilité (p) est la probabilité purement combinatoire de victoire du pari, en supposant chaque cheval équiprobable.
Coefficient binomial C(a, b) = a! / (b! (a - b)!)
3. Le Bonus B est la probabilité additionnelle du pari en cas de report du pool quand aucun joueur ne gagne le pari (redistribution des mises vers les positions étendues de la même course (4 premiers, 5 premiers, etc., en Tiercé par exemple).
4. L'espérance mathématique (E) d'un pari de mise unitaire (coût c = 1) est la différence entre le gain espéré (c x r) x p et le coût c
Exemple : Pour une mise c = 1 euro sur le Simple gagnant de rapport moyen historique r = 10, et avec n = 15 chevaux partants, E = (1 x 10) x 1/15 - 1 = -0.33 euro, soit une perte moyenne de 33 % par euro misé.
L'espérance mathématique E montre une perte moyenne de 30 à 60 %, tous paris confondus, mais peut approcher zéro de façon exceptionnelle, notamment sur Tiercé, Quarté+ ou Quinté+ lors de reports importants.
Stratégie gagnante :
Il n'y a pas de stratégie gagnante au jeu du PMU français, mais il existe une stratégie rationnelle visant à réduire la perte.
L'espérance E est positive si et seulement si le rapport r est supérieur à la valeur 1/p. En conséquence, la stratégie rationnelle est la suivante [PER][CHA] :
- Considérer les paris dont le rapport estimé avant course (r) est très proche du seuil critique 1/p du tableau précédent.
- Identifier les favoris sous-joués (cheval ayant une grande probabilité réelle de gagner, mais peu joué, donc avec rapport r élevé).
- Eviter les paris sur des pools fortement sursouscrits (trop de parieurs sur un cheval).
- Diversifier les mises sur plusieurs types de paris.
- Ne pas considérer les paris Tiercé, Quarté+ et Quinté+ comme intrinsèquement préférables en raison d'un bonus éventuel, car les situations de bonus restent statistiquement exceptionnelles.
- Pour les paris simples (un seul cheval), éviter les extrêmes du marché (favori surjoué et outsider spéculatif) et privilégier les chevaux intermédiaires (2e ou 3e favori).
- Pour les paris composés (plusieurs chevaux), construire des combinaisons équilibrées, souvent autour d'un favori solide, en y ajoutant des chevaux intermédiaires susceptibles d'être sous-joués.
B7.8. Sources
[BLE] Bleach-Mx, Comment fonctionne la roulette française ?.
[BON] Bonus Roulette, COMMENT JOUER AU JEU DE LA BOULE AU CASINO ?.
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[CUR] Courses de vecteurs, Course de vecteurs.
[DEL1] Jean-Paul Delahaye, Stratégies magiques au pays de Nim, Pour la Science - n°377 - Mars 2009.
[DEL2] Jean-Paul Delahaye, Les martingales et autres illusions, Pour la Science - n°251 - Septembre 1998.
[GUI1] Guide Roulette, Roulette Européenne.
[GUI2] Guide Roulette, Roulette Américaine.
[JEU] Jeux Solo ici et là, ACCORDEON #31 (Youtube, 11:54).
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[ROU1] Roulette 17, Tiers Du Cylindre.
[ROU2] Roulette 17, Voisins Du Zero.
[ROU3] Roulette 17, Orphelins.
[ROU4] Roulette 17, Jeu Zero.
[TOU] Pierre Tougne, Roulette, Loto et probabilités, La mathématique des jeux, pp.147-156, Pour la Science, 1991.
[TRI1] Jean Tricot, Jeux et informatique - Le jeu des pièces de 10 francs, Science et Vie - n°722 - Novembre 1977.
[TRI2] Jean Tricot, Jeux et informatique - Le jeu de Northcott, Science et Vie - n°724 - Janvier 1978.
[WIK1] Wikipedia, Bataille (jeu).
[WIK2] Wikipedia, Bataille navale(jeu).
[WIK3] Wikipedia, Racetrack (game).
[WIK4] Wikipedia, Crapette.
[WIK5] Wikipedia, Yahtzee.
[WIK6] Wikipedia, Pig (dice game).
[WIK7] Wikipedia, Morpion (jeu).
[WIK8] Wikipedia, Tic-tac-toe.
[WIK9] Wikipedia, Poker.
[WIK10] Wikipedia, Roulette (jeu de hasard).
Voir détail.
Les constellations, regroupements apparents d'étoiles formant des figures imaginaires dans le ciel, ont fasciné l'humanité depuis des millénaires.
Aujourd'hui, 88 constellations officielles servent à cartographier le ciel. Certaines, comme la Petite Ourse ou Cassiopée, sont visibles toute l'année, tandis que d'autres, comme le Cygne en été ou Orion en hiver, ne se dévoilent qu'en certaines saisons.
Les constellations zodiacales, traversées par le Soleil au cours de l'année, font partie de ces 88 officielles et jouent un rôle particulier en astrologie.
L'observation du ciel révèle également des étoiles remarquables, telles que Sirius ou Vega, véritables points de repère dans la voûte céleste. Pour en profiter au mieux, il est alors important de suivre certains conseils pratiques d'observation.
C4.1. Généralités [CHA][PER] :
Définitions :
- Une constellation est un groupement apparent d'étoiles dans le ciel nocturne, vu depuis la Terre.
- Une constellations circumpolaire est une constellation qui, pour un observateur situé à une latitude donnée (nord ou sud), reste visible toute l'année.
- Une constellation saisonnière est une constellation non-circumpolaire, donc visible uniquement pendant ou autour d'une saison donnée, et absente du ciel nocturne le reste de l'année.
- L'écliptique est le plan de l'orbite terrestre autour du Soleil ou, vu depuis la Terre, le cercle tracé par le Soleil sur la voûte céleste au cours d'une année.
- L'horizon est la ligne circulaire horizontale où le ciel et la Terre (ou la mer) semblent se rejoindre.
- Le zénith est le point du ciel situé exactement à la verticale de l'observateur, au-dessus de sa tête.
- Le pôle nord céleste est le point du ciel situé au-dessus de l'horizon nord, à une hauteur égale à la latitude de l'observateur. Pour Paris (environ 49° de latitude nord), sur une carte du ciel en disque rotatif, ce point apparaît à mi-chemin entre le centre du disque (zénith) et son bord nord (horizon nord). Pour utiliser correctement le disque, il faut le tenir au-dessus de la tête et orienter le bord nord du disque vers le nord géographique, à l'aide d'une boussole par exemple.
- Attention : sur une carte du ciel, les directions est et ouest sont inversées par rapport à une carte géographique classique, afin de correspondre au point de vue de l'observateur tenant sa carte vers le ciel. Retourner une carte (la mettre à l'envers) tout en gardant le nord devant soi inverse en effet la droite et la gauche.
- L'étoile polaire (Polaris) est un excellent représentant du pôle nord céleste, par lequel passe l'axe de rotation propre de la Terre. L'écart angulaire entre ces deux points (environ 0°38' en 2025) est en effet imperceptible à l'oeil nu car le pôle nord céleste n'est qu'un point abstrait du ciel, situé très près de Polaris.
Mouvement et position des constellations :
- Le mouvement des constellations est le suivant : en raison de la rotation quotidienne de la Terre sur elle-même, toutes les constellations visibles depuis l'hémisphère nord décrivent un cercle autour de Polaris en 24 heures, dans le sens inverse des aiguilles d'une montre, mais seules les circumpolaires restent toujours visibles. Les saisonnières passent sous l'horizon lors de leur rotation avec un lever à l'est et un coucher à l'ouest chaque jour.
- La position géométrique relative entre les constellations, ainsi qu'entre les étoiles d'une même constellation, ne change pas de manière significative au cours de la rotation quotidienne de la Terre (mouvement diurne), ni pendant sa révolution annuelle autour du Soleil (mouvement saisonnier). Cela s'explique par la très grande distance existant entre la Terre et les étoiles de ces constellations. Seul change la portion du ciel visible depuis un lieu donné sur Terre à un moment précis.
- La "main ouverte" est un bon repère pour mesurer une distance entre deux points dans le ciel : tenez la main à bout de bras, doigts écartés, et considérez la largeur qui s'étend du bout du pouce au bout du petit doigt. Cette largeur correspond à un écart angulaire d'environ 20° mesuré depuis l'observateur.
Etoiles, planètes, Lune, satellites artificiels, avions, étoiles filantes, amas stellaire :
- Les étoiles scintillent. Ce phénomène est dû à la turbulence de l'atmosphère terrestre qui perturbe la lumière provenant de ces sources ponctuelles très éloignées.
- Les planètes du système solaire, en revanche, ne scintillent pas ou très peu. Elles sont en effet beaucoup plus proches de la Terre et apparaissent à l'oeil nu sous forme de points lumineux tout comme les étoiles, et au téléscope sous forme de petits disques lumineux.
- Les planètes et la Lune ne traversent que les constellations du zodiaque astronomique, jamais les constellations circumpolaires ni les constellations saisonnières non zodiacales. En effet, les planètes et la Lune restent toujours très proches de l'écliptique, tandis que ces constellations sont situées loin de l'écliptique (les circumpolaires autour du pôle céleste, nord ou sud, les saisonnières non zodiacales ailleurs dans le ciel).
- Les planètes et la Lune ne sont pas circumpolaires : elles se lèvent et se couchent chaque jour, tout en se déplaçant graduellement par rapport aux étoiles lointaines du fond du ciel. La Lune avance d'environ 13° vers l'est chaque jour par rapport à ces étoiles et met donc 27,3 jours pour effectuer un tour complet apparent autour de l'étoile polaire. Les planètes se déplacent bien plus lentement et mettent plusieurs années, selon la planète, pour effectuer un tour complet.
- La Lune est absente du ciel nocturne pendant les nuits proches de la nouvelle lune selon certains horaires (voir Conseils pour bien observer), ce qui permet une observation optimale des constellations.
- Les satellites artificiels en orbite terrestre basse apparaissent sous forme d'un point lumineux blanc, non clignotant, qui traverse le ciel d'ouest en est en quelques minutes.
- Les avions évoluant à haute altitude apparaissent sous forme d'un point lumineux blanc et clignotant (feu stroboscopique anticollision), qui se déplace plus lentement que les satellites artificiels. A moyenne ou basse altitude, les avions se distinguent par plusieurs points lumineux colorés fixes (feux de position), en plus du point blanc clignotant, tous ces points pouvant apparaître séparés ou fusionnés selon la distance à l'observateur.
- Les étoiles filantes (ou météores) sont des traînées lumineuses visibles une à deux secondes. Elles proviennent de nuages de poussières laissées par des comètes ou des astéroïdes. Chaque année, la Terre croise l'orbite de ces nuages, faisant brûler leurs poussières au contact de l'atmosphère terrestre. On observe 5 à 10 étoiles filantes par heure en moyenne, et jusqu'à 50 à 100 lors des pics d'activité de ces nuages météoritiques, notamment entre mi-juillet et mi-août dans la constellation de Persée, et début à mi-décembre dans la constellation des Gémeaux.
- Un amas stellaire est un groupement local d'étoiles liées entre elles par la gravitation, nées d'une même région de gaz et de poussières au sein d'une même galaxie. Vu depuis la Terre, il apparaît projeté dans une constellation.
Objets brillants :
Les objets naturels les plus brillants du ciel nocturne terrestre, visibles depuis l'hémisphère nord, sont les suivants, par ordre décroissant de brillance :
C4.2. Liste des constellations :
L'Union Astronomique Internationale (UAI) a défini 88 constellations officielles en 1922 [IAU1]. Elles couvrent la totalité de la sphère céleste, répartie entre l'hémisphère nord et sud.
Elles se répartissent comme suit :
* 54 constellations visibles totalement ou partiellement depuis la France métropolitaine :
- 7 constellations visibles toute l'année
- 20 constellations saisonnières visibles pendant l'été étendu (de mai à octobre)
- 15 constellations saisonnières visibles pendant l'hiver étendu (de novembre à avril)
- 12 constellations difficiles à voir à l'oeil nu
* 34 constellations non visibles depuis la France métropolitaine
Les 54 constellations visibles totalement ou partiellement depuis la France métropolitaine sont les suivantes, classées par ordre alphabétique :
Ces constellations sont décrites ci-dessous, en les classant par période de l'année puis par position dans le ciel, selon les définitions suivantes :
|
En synthèse, les constellations sont ensuite localisées précisément dans le ciel selon une représentation neutre qui n'utilise ni points cardinaux, ni notions directionnelles relatives, ni position de l'observateur sur Terre, ni référence à l'heure ou au jour dans l'année. Cette méthode de repérage céleste, développée par l'Auteur, repose exclusivement sur les principes suivants : - L'identification initiale d'étoiles ou de constellations majeures, visibles et reconnaissables sans erreur à l'oeil nu. - La construction de lignes droites imaginaires entre ces repères célestes, permettant une triangulation récursive : chaque nouveau repère est localisé par alignement géométrique avec les repères déjà identifiés, ce qui étend progressivement la carte mentale du ciel. - L'estimation des distances angulaires apparentes à l'aide de la largeur d'une main ouverte tendue à bout de bras, utilisée comme unité de mesure naturelle et universelle. Cette méthode pragmatique est particulièrement adaptée à l'apprentissage progressif de l'astronomie visuelle et à la navigation céleste sans instrument. |
C4.3. Constellations visibles toute l'année :
Les constellations visibles toute l'année (constellations circumpolaires) depuis la France métropolitaine sont les suivantes (voir Figures ci-dessous [IST][LES]) :




|
Synthèse : Pour trouver dans le ciel ces constellations, la méthode la plus simple est la suivante [DAR][CHA][PER], en se reportant aux cartes ci-dessus : - Carte du 25 juillet 2025 à 0h00 pour France métropolitaine ou latitudes de 40 à 55°N, avec zénith au centre de la portion de ciel visible [STE]. - Guide de localisation des constellations circumpolaires (en représentation neutre). 1a. Trouver la Grande Ourse : grande casserole avec sept étoiles brillantes, située dans la moitié nord du ciel. Sa hauteur est basse (proche de l'horizon) en automne et en hiver, et très haute (proche du zénith) au printemps et en été. Sa longueur, du bout du manche (η) au bord externe (α ou β) de la casserole, correspond à une largeur de main ouverte. 1b. Trouver l'étoile polaire Polaris : étoile brillante située près de la Grande Ourse dans le prolongement du bord externe de la casserole, en direction opposée à son fond, à une distance équivalente à une largeur de main ouverte ou à cinq fois la distance entre les deux étoiles (α et β) de ce bord (voir Figure 1 ci-dessus). Trouver la Petite Ourse : petite casserole avec trois étoiles brillantes, dont Polaris (α) à l'extrémité du manche et deux étoiles (β et γ) au bord externe de la casserole (voir Figure 1 ci-dessus). Les quatre étoiles intermédiaires (δ, ε, ζ, η) sont souvent peu visibles. 2. Trouver Cassiopée : forme caractéristique en W, située à l'opposé du centre de la Grande Ourse (point d'attache du manche de la casserole) par rapport à Polaris. 3. Trouver le Dragon : sa tête est un carré déformé de quatre étoiles brillantes (γ β, ν, ξ) situé près de la Grande Ourse, à deux largeurs de main ouverte, en traçant depuis l'extrémité (η) du manche de la casserole une perpendiculaire dans la direction où le manche est courbé. Le corps (δ, ζ, η, ι, α) et la queue (λ) du Dragon forment un grand S inversé (comme vu dans un miroir) de six étoiles brillantes qui s'enroule partiellement entre la Grande Ourse et la Petit Ourse. 4. Trouver Céphée : polygone à sept étoiles brillantes formant une maison d'enfant (rectangle α, β, ι, ζ) à toit pointu (γ), situé à mi-chemin entre Cassiopée et la tête du Dragon. 5. Trouver la Girafe : groupe de neuf étoiles dont un long cou (α, HD 42818, HD 49878, VZ) pointant vers Polaris. L'étoile la plus brillante (β) est située à l'opposé de la tête du Dragon par rapport à Polaris. 6. Trouver le Lynx : ligne brisée de sept étoiles dont trois brillantes (α, 38, 10 UMa), visible complètement en fin d'hiver et au printemps, située près de la Grande Ourse, à une largeur de main ouverte, dans le prolongement du fond de la casserole, en direction opposée au manche. |
C4.4. Constellations saisonnières d'été :
Les constellations saisonnières visibles uniquement pendant l'été étendu (de mai à octobre) depuis la France métropolitaine sont les suivantes (voir Figures ci-dessous [IST][LES]) :






|
Synthèse : Pour trouver dans le ciel d'été ces constellations, la méthode la plus simple est la suivante [CHA][PER], en se reportant aux cartes ci-dessus : - Triangle d'été. - Carte du 25 juillet 2025 à 0h00 pour France métropolitaine ou latitudes de 40 à 55°N, avec zénith au centre de la portion de ciel visible [STE]. - Guide de localisation des constellations saisonnières d'été (en représentation neutre). 0. Trouver le Triangle d'été situé proche du zénith vers minuit en été (juillet à septembre) : triangle quasi-équilatéral formé de trois étoiles super brillantes : Vega (Lyre), Altair (Aigle) et Deneb (Cygne). La distance entre chaque étoile correspond à une largeur de main ouverte. 1. Trouver l'étoile Vega, étoile la plus brillante du Triangle d'été, de couleur bleue-blanche. Vega est située près de la tête du Dragon, sur une ligne venant de l'extrémité du manche de la Grande Ourse et passant par la tête du Dragon. Trouver la Lyre : petit parallélogramme de quatre étoiles, dont deux brillantes (β, γ), relié à Vega (α) et prolongeant cette ligne depuis Vega. 2. Trouver l'étoile Altair, étoile du Triangle d'été, flanquée de deux petites étoiles (β et γ), située près de Vega à une largeur de main ouverte, sur une ligne venant de l'extrémité du manche de la Grande Ourse et passant par Vega. Trouver l'Aigle : grande figure située à gauche de cette ligne en arrivant à Altair (α), composée d'une tête (γ-α-β) centrée sur Altair, de deux ailes droites (δ-ζ et δ-θ) tournées vers la tête, d'un corps linéaire (α-δ-λ) et d'une queue (λ). 3. Trouver l'étoile Deneb, étoile du Triangle d'été, située à droite de la ligne allant de Vega à Altair, à mi-chemin entre Altair et Cassiopée. Trouver le Cygne : grande croix composée d'une queue (α, Deneb), d'un corps (α-γ), de deux ailes brisées (γ-ε-ζ et γ-δ-ι) tournées vers la queue, d'un long cou (γ-η-β) tourné vers Altair, et d'une tête (β). 4. Trouver l'étoile Arcturus, étoile super brillante de couleur orange, située dans le prolongement du manche de la Grande Ourse, à une largeur de main ouverte. Trouver le Bouvier : groupe de sept étoiles brillantes en forme de cerf-volant, situé à droite de cette ligne avant d'arriver à Acturus (α). 5. Trouver la Couronne Boréale : demi-cercle de sept étoiles dont trois brillantes (α, β, γ), situé près d'Arcturus, à gauche de la ligne allant de Arcturus à Vega. 6. Trouver Hercule : groupe de quatorze étoiles brillantes, dont quatre formant un carré (ε, ζ, π, η) situé près de Vega, à gauche de la ligne allant de Acturus à Vega. 7. Trouver l'étoile Antares, étoile super brillante, isolée, de couleur rouge, située très bas sur l'horizon sud de mai à août, sur une ligne venant de Deneb et passant par Vega, à trois largeurs de main ouverte de Vega. Trouver le Scorpion : grand S à dix-neuf étoiles brillantes entourant Antares (α), coeur du Scorpion, avec ses deux petites pinces (β1 - δ et ρ - π) situées à l'ouest d'Antares (à gauche de la ligne allant de Vega à Antares). 8. Trouver la Balance : polygone à six étoiles brillantes, dont quatre formant un rectangle (α2, β, γ, σ), situé à l'ouest de Antares (à gauche de la ligne allant de Vega à Antares), à une largeur de main ouverte de Antares. 9. Trouver le Sagittaire : groupe de quinze étoiles brillantes, situé à l'est de Antares (à droite de la ligne allant de Vega à Antares), à deux largeurs de main ouverte de Antares. 10a. Trouver Ophiuchus : polygone à douze étoiles brillantes, dont cinq formant un pentagone irrégulier (α, β, η, ζ, δ) situé à mi-chemin entre Antares et Vega. 10b. Trouver le Serpent : groupe d'étoiles brillantes situé de part et d'autre d'Ophiuchus (six pour la tête du serpent formant un Y et une pour la queue) 11. Trouver Pégase : groupe de onze étoiles brillantes, dont quatre formant un grand carré vide (α, β, γ, δ) situé près de Deneb, à deux largeurs de main ouverte, sur une ligne venant de Vega et passant par Deneb. 12. Trouver Andromède : groupe de huit étoiles brillantes touchant Pégase, dont une ligne brisée de quatre étoiles (α, δ, β, γ) située à l'opposé de Polaris par rapport à Cassiopée. 13. Trouver les Poissons : grand V à trois étoiles brillantes. Sa base (α Piscium) se trouve dans le prolongement d'un des côtés du grand carré de Pégase comme suit : 1. Identifier l'étoile (δ) la plus brillante du carré, 2. Identifier le coin (α) opposé en diagonale, 3. Identifier le coin suivant (γ) dans le sens horaire depuis α, 4. Prolonger la ligne α-γ sur une distance équivalente à une largeur de main ouverte. 14. Trouver la Baleine : polygone de six étoiles brillantes prolongé par une ligne de trois autres brillantes. La bouche (β) de la Baleine, étoile la plus brillante, se trouve dans le prolongement d'un des côtés du grand carré de Pégase comme suit : 1. Identifier l'étoile (δ) la plus brillante du carré, 2. Identifier le coin suivant (γ) dans le sens anti-horaire depuis δ, 4. Prolonger la ligne δ-γ sur une distance équivalente à une largeur de main ouverte. 15. Trouver le Verseau : groupe de huit étoiles brillantes, dont quatre formant une ligne brisée (δ, α, β, ε) située dans le prolongement d'une diagonale du grand carré de Pégase comme suit : 1. Identifier l'étoile (δ) la plus brillante du carré, 2. Identifier le coin (α) opposé en diagonale, 3. Prolonger la ligne δ-α sur une distance équivalente à une largeur de main ouverte. 16. Trouver le Capricorne : triangle aplati à huit étoiles brillantes, situé à l'opposé de Vega par rapport à Altair. 17. Trouver la Flèche : flèche à quatre étoiles dont deux brillantes (γ, δ), située près de Altair, à droite de la ligne allant de Altair à Deneb. 18. Trouver le Dauphin : petit losange de quatre étoiles dont deux brillantes (α, β), prolongé par une queue (ε) et situé près de Altair, à gauche de la ligne allant de Altair à Pégase. 19. Trouver l'Ecu : petit losange allongé à quatre étoiles dont une brillante (α), situé à côté de la queue de l'Aigle (λ). |
C4.5. Constellations saisonnières d'hiver :
Les constellations saisonnières visibles pendant l'hiver étendu (de novembre à avril) depuis la France métropolitaine sont les suivantes (voir Figures ci-dessous [IST][LES]) :




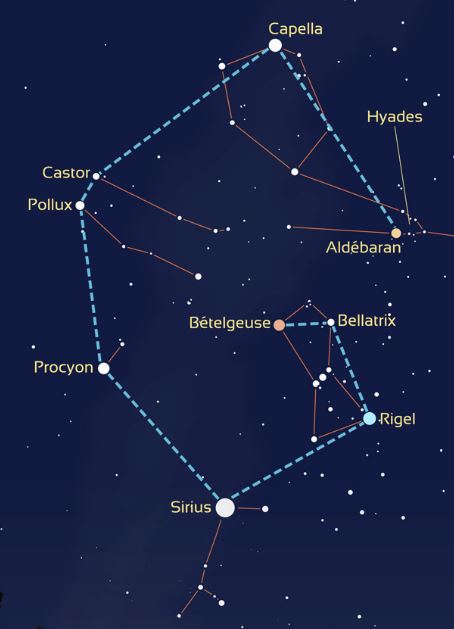
|
Synthèse : Pour trouver dans le ciel d'hiver ces constellations, la méthode la plus simple est la suivante [CHA][PER], en se reportant aux cartes ci-dessus : - Triangle d'hiver et hexagone d'hiver. - Carte du 14 février 2025 à 0h00 pour France métropolitaine ou latitudes de 40 à 55°N, avec zénith au centre de la portion de ciel visible [STE]. - Le "Grand G". - Guide de localisation des constellations saisonnières d'hiver (en représentation neutre). 0. Trouver le Triangle d'hiver situé bas au-dessus de l'horizon sud vers minuit en hiver (décembre à février) : triangle quasi-équilatéral, quasi-vide d'étoiles, formé de trois étoiles super brillantes : Sirius (Grand Chien), Procyon (Petit Chien) et Betelgeuse (Orion). La distance entre chaque étoile correspond à une largeur de main ouverte. 1. Trouver l'étoile Sirius, étoile la plus brillante et la plus basse du Triangle d'hiver, de couleur bleue-blanche. Trouver le Grand Chien : trapèze de quatre étoiles brillantes (α, β, ε, δ) dont Sirius (α), prolongeant la ligne Polaris-Sirius depuis Sirius (α). 2. Trouver l'étoile Procyon, étoile la plus à l'est du Triangle d'hiver (à droite de la ligne allant de Polaris à Sirius), de couleur blanche. Trouver le Petit Chien : groupe de deux étoiles brillantes (α, β) dont Procyon (α), tourné vers cette ligne. 3. Trouver l'étoile Betelgeuse, étoile la plus à l'ouest du Triangle d'hiver (à gauche de la ligne allant de Polaris à Sirius), de couleur rouge. Trouver Orion : grand rectangle (α, γ, β, κ) dont Betelgeuse (α), traversé en son centre par une ceinture de trois étoiles alignées (ζ, ε, δ). Remarque importante : cette méthode de repérage peu courante (d'abord Sirius qui est immanquable, puis Orion) semble plus adaptée pour les observateurs débutants que la méthode classique inverse (d'abord Orion puis Sirius). 4. Trouver le Lièvre : trapèze à quatre étoiles brillantes (α, β, ε, μ), situé près de la ceinture d'Orion, sur une ligne venant de Polaris et passant par la ceinture d'Orion. 5. Trouver l'étoile Aldebaran, étoile super brillante de couleur orange, située près d'Orion, à droite de la ligne venant de Sirius et passant par Betelgeuse, à une largeur de main ouverte de Betelgeuse. Trouver le Taureau : grand V à onze étoiles brillantes dont Aldebaran (α), oeil du Taureau, situé tout près de la base du V. 6. Trouver l'étoile Capella, étoile super brillante de couleur jaune, située à mi-chemin entre la ceinture d'Orion et Polaris. Trouver le Cocher : hexagone à six étoiles brillantes (α, β, θ, γ, ι, ε) dont Capella (α), touchant le Taureau et tourné vers Orion. 7. Trouver l'étoile Mirfak, étoile super brillante de couleur blanche, située à mi-chemin entre Capella et Cassiopée. Trouver Persée : grand Y à trois branches (α-β, α-γ et α-δ-ε-ζ) centré sur Mirfak (α). 8. Trouver l'étoile Hamal, étoile brillante située à l'opposé de la tête du Dragon par rapport à Cassiopée. Trouver le Bélier : ligne brisée de trois étoiles brillantes (β, α, 41) dont Hamal (α). 9. Trouver le Triangle : triangle allongé de trois étoiles brillantes, situé près de Hamal entre Hamal et Polaris. 10. Trouver les étoiles Castor et Pollux, deux étoiles rapprochées super brillantes (Castor, blanche, et Pollux, orange), situées près de Procyon entre Procyon et Polaris. Trouver les Gémeaux : groupe de onze étoiles brillantes dont Castor (α) et Pollux (β), formant un grand rectangle allongé (α, β, γ, μ) tourné vers Orion. 11. Trouver le Cancer : grand Y à quatre étoiles brillantes, situé à l'opposé de Sirius par rapport à Procyon. 12. Trouver l'étoile Regulus, étoile super brillante de couleur bleue, située à gauche de la ligne venant de Sirius et passant par Procyon, à deux largeurs de main ouverte de Procyon, et située aussi à l'opposé de la tête du Dragon par rapport au centre de la Grande Ourse (point d'attache du manche de la casserole). Trouver le Lion : groupe de neuf étoiles brillantes formant un trapèze aplati de quatre étoiles (α, β, δ, γ) dont Regulus (α), et prolongé par une tête (ε) et une crinière (ε, μ, ζ, γ). 13. Trouver l'étoile Spica, étoile super brillante de couleur bleue, située bas dans le ciel, sur une ligne venant de Sirius et passant par Procyon, à cinq largeurs de main ouverte de Procyon. Trouver la Vierge : groupe de neuf étoiles brillantes dont Spica (α). 14. Trouver le Corbeau : polygone de cinq étoiles dont quatre brillantes (β, δ, γ, ε), situé bas dans le ciel, à l'ouest de Spica (à gauche de la ligne allant de Sirius à Spica), à une largeur de main ouverte de Spica. 15. Trouver la Coupe : polygone de quatre étoiles dont une brillante (δ), situé bas dans le ciel, à l'ouest du Spica (à gauche de la ligne allant de Sirius à Spica), à deux largeurs de main ouverte de Spica. Remarquer l'Hexagone d'hiver proche du zénith vers minuit en hiver (décembre à février) : hexagone symétrique à six étoiles super brillantes : Sirius (Grand Chien), Procyon (Petit Chien), Pollux (Gémeaux), Capella (Cocher), Aldebaran (Taureau), Rigel (Orion). Remarquer le "Grand G" proche du zénith vers minuit en hiver (décembre à février) : grand G à neuf étoiles super brillantes : Betelgeuse, Bellatrix et Rigel (Orion), Sirius (Grand Chien), Procyon (Petit Chien), Pollux et Castor (Gémeaux), Capella (Cocher), Aldebaran (Taureau). |
C4.6. Autres constellations :
Les autres constellations sont les suivantes :
12 constellations difficiles à voir à l'oeil nu :
* Constellations trop proches de l'horizon :
- La Colombe (Columba, Col)
- L'Eridan (Eridanus, Eri)
- L'Hydre (Hydra, Hya)
- Le Poisson Austral (Piscis Austrinus, PsA)
* Constellations trop faibles en brillance (aucune étoile n'ayant une magnitude inférieure à 4.0) :
- La Chevelure de Bérénice (Coma Berenices, Com)
- Le Lézard (Lacerta, Lac)
- Le Petit Lion (Leo Minor, LMi)
- Le Petit Renard (Vulpecula, Vul)
- Le Sextant (Sextans, Sex)
* Constellations noyées dans des régions denses en étoiles :
- Les Chiens de chasse (Canes Venatici, CVn)
- La Licorne (Monoceros, Mon)
- Le Petit Cheval (Equuleus, Equ)
34 constellations non visibles depuis la France métropolitaine :
- L'Autel (Ara, Ara)
- La Boussole (Pyxis, Pyx)
- Le Burin (Caelum, Cae)
- Le Caméléon (Chamaeleon, Cha)
- La Carène (Carina, Car)
- Le Centaure (Centaurus, Cen)
- Le Compas (Circinus, Cir)
- La Couronne Australe (Corona Australis, CrA)
- La Croix du Sud (Crux, Cru)
- L'Equerre (Norma, Nor)
- Le Fourneau (Fornax, For)
- La Grue (Grus, Gru)
- L'Horloge (Horologium, Hor)
- L'Hydre Mâle (Hydrus, Hyi)
- L'Indien (Indus, Ind)
- Le Loup (Lupus, Lup)
- La Machine Pneumatique (Antlia, Ant)
- Le Microscope (Microscopium, Mic)
- La Mouche (Musca, Mus)
- L'Octant (Octans, Oct)
- L'Oiseau de Paradis (Apus, Aps)
- Le Paon (Pavo, Pav)
- Le Peintre (Pictor, Pic)
- Le Phénix (Phoenix, Phe)
- Le Poisson Doré (Dorado, Dor)
- Le Poisson Volant (Volans, Vol)
- La Poupe (Puppis, Pup)
- Le Réticule (Reticulum, Ret)
- Le Sculpteur (Sculptor, Scl)
- La Table (Mensa, Men)
- Le Télescope (Telescopium, Tel)
- Le Toucan (Tucana, Tuc)
- Le Triangle Austral (Triangulum Australe, TrA)
- Les Voiles (Vela, Vel)
C4.7. Constellations zodiacales :
Le zodiaque astronomique est une bande dans le ciel qui s'étend d'environ 8° de part et d'autre de l'écliptique.
Il comprend treize constellations officielles qui sont les seules que le Soleil masque au cours de son parcours annuel, vu de la Terre.
Le zodiaque astrologique reprend les noms et la succession des constellations du zodiaque astronomique, mais se limite à douze signes en excluant Ophiuchus, afin de diviser symboliquement l'écliptique en douze parts égales.
Le point vernal (équinoxe de printemps) marquait autrefois l'entrée du Soleil dans la constellation du Bélier, ce qui a justifié son statut de premier signe du zodiaque. Mais aujourd'hui, en raison de la précession des équinoxes, ce point se situe dans la constellation des Poissons.
Les constellations du zodiaque sont les suivantes, listées dans l'ordre où le Soleil les traverse :
Leur visibilité depuis l'hémisphère nord est la suivante :
* Constellations visibles toute l'année : aucune.
* Constellations saisonnières d'été (de mai à octobre) : Balance, Scorpion, Ophiuchus, Sagittaire, Capricorne, Verseau, Poissons.
* Constellations saisonnières d'hiver (de novembre à avril) : Bélier, Taureau, Gémeaux, Cancer, Lion, Vierge.
C4.8. Conseils pour bien observer :
Pour bien observer les étoiles, constellations, planètes et satellites dans le ciel, il est conseillé de [CHA][PER] :
C4.9. Coordonnées, couleur et magnitude d'un astre :
Les coordonnées d'un astre sont généralement les coordonnées équatoriales (α et δ) définies comme suit (voir Figure ci-dessus) :
- Sphère céleste : sphère imaginaire de rayon infini, centrée sur la Terre, sur laquelle sont projetés tous les astres observés depuis la Terre.
- Equateur céleste : grand cercle imaginaire tracé sur la sphère céleste, correspondant à la projection de l'équateur terrestre sur cette sphère.
- Point vernal (γ) : point d'intersection de l'équateur céleste et de l'écliptique au moment de l'équinoxe de printemps dans l'hémisphère nord.
- Ascension droite (α) : angle horaire mesuré le long de l'équateur céleste, vers l'est à partir du point vernal, entre le méridien passant par ce point et celui passant par l'astre. Elle s'exprime en heures, de 0 à 24 h, avec la correspondance : 1 h = 15°. L'ascension droite est l'analogue céleste de la longitude terrestre.
- Déclinaison (δ) : angle mesurant la distance d'un astre par rapport à l'équateur céleste. Elle s'exprime en degrés, de -90° (pôle sud céleste) à +90° (pôle nord céleste). La déclinaison est l'analogue céleste de la latitude terrestre.
Exemple pour l'étoile Vega [IAU2] : α = 18 h 36 min 56.345 s (soit 279.234735°), δ = +38° 47' 01.28" (soit +38.783689°).
La distance angulaire (d) séparant deux astres dans le ciel, mesurée depuis la Terre, est donnée par la formule suivante de trigonométrie sphérique :
cos(d) = sin(δ1) sin(δ2) + cos(δ1) cos(δ2) cos(α1 - α2)
où α1 et α2 sont les ascensions droites des deux astres, δ1 et δ2 leurs déclinaisons.
La couleur apparente des astres (vue à l'oeil nu) dépend principalement de leur température de surface selon le classement simplifié suivant :
- Bleu : astres très chauds ( > 10 000 K environ), comme Spica.
- Blanc : astres chauds (de 6 000 à 10 000 K environ), comme Sirius.
- Jaune : astres de température moyenne (de 5 200 à 6 000 K environ), comme le Soleil.
- Orange : astres froids (de 3 700 à 5 200 K environ), comme Aldebaran.
- Rouge : astres très froids ( < 3 700 K environ), comme Betelgeuse.
Cependant, des facteurs influencent sensiblement la couleur apparente :
- La brillance (effet blanchâtre pour les astres très lumineux)
- L'atmosphère terrestre (effet rougeâtre près de l'horizon dû à la diffusion de la lumière dans l'air)
- La poussière interstellaire (accentuation du rouge par absorption des longueurs d'onde courtes (bleu))
- Les nuages de gaz interstellaires (absorption et diffusion de certaines longueurs d'onde selon leur composition)
- La sensibilité de l'oeil humain (atténuation du bleu et du rouge dans l'obscurité)
Attention : contrairement aux idées courantes (rouge = chaud, et bleu = froid), plus on va du rouge au bleu, plus l'astre a une température de surface élevée.
La magnitude apparente (M) d'un astre correspond à son état de brillance perçu depuis la Terre :
M = -2.5 log10[F/F0]
avec :
F = flux lumineux reçu de l'astre (en W/m2)
F0 = flux lumineux de référence correspondant à M = 0 (historiquement celui de Vega, avant les mesures actuelles plus précises).
M est une mesure normalisée qui tient compte de quatre facteurs :
- La luminosité intrinsèque de l'astre. Elle correspond à la puissance totale de lumière (L en Watt) émise au niveau de sa surface, puis diffusée uniformément dans toutes les directions à travers une surface sphérique de rayon croissant r.
- La distance entre l'astre et le Terre. La luminosité apparente (I en W/m2), perçue à la distance r de l'astre, diminue en effet selon la loi de l'inverse du carré : I = L/(4 π r2).
- L'extinction (absorption et diffusion de la lumière par l'atmosphère terrestre, les poussières interstellaires et les nuages de gaz entre l'astre et la Terre)
- La sensibilité de l'oeil humain (qui perçoit la luminosité apparente selon une échelle logarithmique inverse)
Attention : plus la valeur numérique (M) de la magnitude apparente est faible, plus l'astre est brillant.
C4.10. Sources relatives aux constellations :
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[DAR] Découvrir le ciel à l'oeil nu, Bertrand D'Armagnac et Carine Souplet, Stelvision.
[IAU1] IAU, Les constellations.
[IAU2] IAU, Comment sont nommées les étoiles ? ou Current List of IAU Star Names.
[IMA] Imago Mundi, Les 88 constellations.
[IST] iStock, Constellations.
[IMA] Imago Mundi, Ophiuchus.
[LES] Les Astronautes, Comment reconnaître les constellations dans le ciel ?.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[STE] Stelvision, Carte du ciel du jour (pour France métropolitaine ou latitudes de 40 à 55°N, avec zénith au centre de la portion de ciel visible).

La Lune exerce une influence subtile mais réelle sur la vie terrestre. Par ses cycles et sa gravitation, elle rythme les marées, guide certains comportements animaux et semble affecter la croissance des plantes. Chez l'être humain, ses effets sont plus difficiles à démontrer de manière certaine.
L'influence de la Lune fait l'objet de nombreux dictons.
C8.1. L'influence de la Lune sur les animaux :
Chez les animaux, la Lune influence leur comportement principalement par la luminosité accrue lors de la pleine lune. Cette clarté nocturne modifie notamment les cycles de chasse et de reproduction.
Ainsi, les prédateurs comme les chats ou les hiboux chassent plus efficacement grâce à une meilleure luminosité, tandis que les proies comme les rongeurs ou les insectes réduisent leur déplacement pour limiter les risques d'être repérées.
Dans le milieu marin, de nombreuses espèces synchronisent leur reproduction avec les cycles lunaires, influencées à la fois par la luminosité et par les marées.
Les animaux domestiques sont parfois plus agités lors des nuits de pleine lune, probablement en raison de cette luminosité inhabituelle.
C8.2. L'influence de la Lune sur les êtres humains :
Chez les humains, l'influence de la Lune sur le sommeil, l'humeur, les naissances ou les comportements fait l'objet d'études souvent contradictoires ou peu concluantes.
En revanche, l'effet perçu de la Lune pourrait relever d'un phénomène psychologique : les gens ont tendance à se souvenir davantage des événements inhabituels lorsqu'ils coïncident avec la pleine lune, tout en oubliant les périodes sans événement notable.
C8.3. L'influence de la Lune sur les plantes :
L'influence de la Lune sur la croissance des plantes a toujours suscité un vif débat entre les scientifiques et les adeptes de la biodynamique.
Selon l'approche biodynamique héritée des travaux de Rudolf Steiner, les cycles solaires et lunaires, ainsi que les autres rythmes cosmiques, seraient l'expression de forces cosmiques incluant la Lune, le Soleil et les planètes. La sève monterait dans les plantes pendant la Lune ascendante, ce qui favoriserait la croissance des parties aériennes comme les feuilles et les fleurs, période propice aux semis et récoltes. A l'inverse, la sève descendrait vers les racines durant la Lune descendante, période propice aux travaux de taille, division, bouturage et récolte des légumes-racines.
Les biodynamiciens considère également que la position de la Lune par rapport aux constellations du zodiaque a une influence spécifique sur la croissance des plantes. Par exemple, quand la Lune est devant la constellation de la Vierge (élément terre), cette période favoriserait particulièrement les racines, tandis que devant la Balance (élément air), elle favoriserait plutôt la croissance des fleurs.
A l'inverse, selon l'approche scientifique, l'influence de la phase lunaire sur la croissance des plantes n'a jamais été établi de manière robuste, claire et reproductible.
Les forces gravitationnelles lunaires, même si elles expliquent les grandes marées océaniques terrestres, sont trop faibles pour avoir un effet significatif sur les plantes prises isolément.
De plus, l'intensité de la lumière lunaire, issue de la réflexion du rayonnement solaire, est insuffisante pour influencer la photosynthèse et d'autres processus biologiques essentiels.
En revanche, il est avéré que les pratiques biodynamiques ont des effets bénéfiques sur la qualité des sols et la biodiversité, mais ces effets sont attribués principalement aux pratiques agricoles et non aux influences directes des forces lunaires ou cosmiques revendiquées par la biodynamique.
Ainsi, pour la science moderne, même si une influence lunaire existe, elle est marginale par rapport aux autres facteurs agronomiques qui conditionnent la gestion des cultures.
Les conditions déterminantes de réussite, reconnus et validés par la recherche agronomique, sont avant tout liées aux facteurs fondamentaux suivants :
1. La qualité du matériel végétal de reproduction (graines, plants, bulbes, boutures) :
- Matériel issu de sources fiables (sain et vigoureux, exempt de maladies et de parasites)
- Variété adaptée au climat local, au pH du sol et à l'exposition (ensoleillée ou ombragée)
2. La nature du sol :
- Drainage du sol pour éviter la stagnation de l'eau autour des racines
- Enrichissement du sol en humus (fumier, compost) et en apports minéraux (chaux, sable, argile)
- Rotation culturale pour éviter maladies et épuisement
- Travail du sol sans le déstructurer pour conserver son activité biologique
3. La protection contre les aléas climatiques :
- Brise-vent (haies, filets, tunnels, serres)
- Anti-gel (voiles d'hivernage, paillage épais, cloches)
- Anti-sécheresse (paillage organique, arrosage adapté)
4. Les pratiques agricoles :
- Respect de la profondeur et de l'espacement des plantations
- Arrosage au bon moment et sans excès d'eau
- Désherbage régulier
- Paillage pour conserver l'humidité et limiter les mauvaises herbes
- Enrichissement de la plante par apport d'engrais (azote, phosphate, potassium)
- Surveillance et traitement phytosanitaire
5. Les périodes de plantation :
- Saison adaptée à chaque variété
- Prise en compte des conditions météorologiques à venir
- Phase lunaire dont l'influence, si elle existe, reste très marginale par rapport aux autres influences
C8.4. Les dictons :
Sont listés ci-dessous les principaux dictons ayant une explication scientifique connue.
Lune et marées :
- La Lune est la maîtresse des marées,
- Quand la Lune rit, l'eau rit aussi : les marées sont directement provoquées par l'attraction gravitationnelle de la Lune (et du Soleil). Et quand la Lune est pleine ou nouvelle, la Terre, la Lune et le Soleil sont alignés (marées de vives-eaux).
Lune et animaux :
- Pleine Lune fait hurler le chien et veiller le coq,
- Quand la Lune est pleine, les bêtes sont en peine,
- Lune claire, loups en colère,
- Quand la Lune s'arrondit, les chiens hurlent à son cri,
- Lune rousse fait souffrir bêtes et pousses : les animaux nocturnes (loups, chiens, oiseaux) réagissent à la luminosité.
Lune et humains :
- Qui dort à la pleine Lune, songe d'infortune,
- Pleine lune fait veiller chacun,
- A la pleine lune, les enfants dorment mal,
- Lune claire rend le coeur en alerte : certaines personnes dorment moins profondément et moins longtemps lors de la pleine Lune.
- Lune claire, amour prospère : la lumière lunaire stimule l'activité nocturne et les sorties sociales.
Lune et plantes :
- Lune montante, sève montante,
- Quand la Lune croît, tout croît,
- Lune descendante, racines grandissantes,
- Quand la Lune décroît, tout décroît : phases lunaires dont l'influence, si elle existe, reste très marginale par rapport aux autres influences.
- Lune rousse, rien ne pousse,
- Lune rousse brûle les jeunes pousses,
- Lune rousse fait souffrir bêtes et pousses : période après Pâques pendant laquelle les nuits claires entraînent une perte de chaleur par rayonnement, rendant une gelée possible.
Lune et météo :
Voir Météo : les dictons
Voir détail.


L'acquisition d'une voiture électrique, qu'elle soit 100 % électrique, hybride ou à hydrogène, nécessite une réflexion approfondie.
Ces différents types de véhicule présentent les avantages et inconvénients suivants par rapport à une voiture classique à motorisation thermique (essence ou diesel).
D3.1. La voiture 100 % électrique
D3.2. La voiture hybride
D3.3. La voiture à hydrogène
D3.4. Synthèse :
|
Statistiques : Fin 2024, le parc électrique roulant français des voitures particulières (hors utilitaires légers) représente environ 8 % du parc roulant total, se répartissant comme suit : 2.2 % (100 % électrique), 1.5 % (hybrides rechargeables) et 4.4 % (hybrides non rechargeables). Achat d'un véhicule 100 % électrique ou hybride : De nombreux acheteurs se focalisent sur le prix d'acquisition, les économies de carburant à court terme et les avantages fiscaux ou écologiques. Mais il faut aussi prendre en compte : - les coûts au-delà de 8 ans, incluant le remplacement éventuel de la batterie. - les dépenses sous-estimées, comme les surcoûts d'assurance, de réparation, de mises à jour logicielles, et le coût de recharge de la batterie, en particulier sur les bornes rapides. - le risque financier qu'un accident mineur endommage la batterie (par exemple, un simple choc contre un trottoir) et entraîne le classement du véhicule comme épave (atteinte du système électrique, choc sur zones sensibles des véhicules électriques, immersion totale ou partielle dans l'eau). - les inquiétudes sur l'autonomie de la voiture 100 % électrique et sur le réseau des bornes de recharge. - le peu de garagistes habilités à intervenir sur des véhicules électriques et hybrides. Pour les ménages aux revenus modestes, deux obstacles majeurs subsistent : le prix élevé à l'achat et le risque de classement en épave après un choc, même léger. Ainsi, l'attrait pour une voiture 100 % électrique ou hybride repose davantage sur des préoccupations environnementales, notamment la réduction des émissions de CO2, que sur une logique strictement économique à court ou long terme. Une décision éclairée passe donc par une analyse complète de tous ces aspects afin de permettre aux acheteurs de faire un choix objectif et adapté à leur situation. A noter que les voitures électriques ayant une garde au sol supérieure, comme les SUV ou Crossovers électriques, offrent une meilleure protection contre les deux risques majeurs pour véhicules électriques : choc au soubassement et immersion accidentelle. Achat d'un véhicule à hydrogène : L'achat d'un véhicule à hydrogène est aujourd'hui plus pertinent pour les flottes professionnelles que pour les particuliers en raison d'un marché encore en développement. Parmi les principaux obstacles, on note : - un prix d'achat élevé, - un réseau insuffisant de stations de ravitaillement en hydrogène, - comme pour les voitures électriques ou hybrides, le risque financier qu'un accident endommage la batterie, voire le réservoir d'hydrogène ou la pile à combustible, et entraîne le classement du véhicule comme épave. Réglementation européenne : A partir de 2035, selon la réglementation européenne publiée au Journal officiel de l'UE le 25 avril 2023 et entrée en vigueur le 15 mai 2023 [EUR] : - La vente de voitures neuves à moteur thermique (essence, diesel et hybrides actuelles), de type voiture particulière ou véhicule utilitaire léger, sera interdite dans l'Union européenne. Seuls les véhicules "zéro émission", comme les voitures 100 % électrique ou celles utilisant des carburants synthétiques (e-fuels) ou de l'hydrogène (FCEV), pourront être commercialisées. - L'interdiction ne s'applique pas au marché de l'occasion. - Les voitures thermiques déjà en circulation ne sont pas concernées et pourront continuer à être utilisées et revendues. Le marché des voitures hybrides, malgré leur succès actuel, est donc amené à disparaître progressivement d'ici 2035, sauf si elles atteignent des performances exceptionnelles en mode électrique. La voiture hybride apparaît ainsi comme une simple étape de transition vers le tout électrique. Secourisme : Les gestes supplémentaires à faire sur un véhicule accidenté de type électrique, hybride ou à hydrogène, sont les suivants : - Identifier et signaler aux secours le type de véhicule car ces véhicules présentent des risques spécifiques concernant notamment la batterie haute tension, le réservoir d'hydrogène haute pression et la gestion du feu. - Maintenir une distance de sécurité d'au moins 30 mètres autour du véhicule accidenté pour éviter tout danger de choc électrique, d'explosion ou d'incendie. - Ne pas utiliser d'eau pour éteindre un feu de batterie sans l'avis des pompiers. Dans le cas rare d'un feu de batterie Lithium-Métal, l'utilisation de l'eau peut aggraver l'incendie. |
D3.5. Sources relatives aux voitures électriques :
[ADE] ADEME, Mondial de l'automobile : l'ADEME publie son avis sur le véhicule électrique : une batterie de taille raisonnable assure une pertinence climatique et économique.
[AUJ1] L'auto-journal, Voitures électriques : quel est le coût des réparations ?.
[AUJ2] L'auto-journal, Véhicules électriques et entretiens : un vrai cauchemar ?.
[AUM] L'Automobile Magazine, Les voitures électriques sont-elles 3 fois plus dangereuses pour les piétons ?.
[AUT] Auto, Attention, les voleurs s'attaquent aux batteries des véhicules hybrides.
[CAP1] Capital, Accidents de la route : dans quels cas votre voiture est-elle jugée irréparable ?.
[CAP2] Capital, Automobile : découvrez pourquoi réparer un véhicule électrique coûte plus cher !.
[CEN] La Centrale, Quand la batterie flanche : dites adieu à votre voiture électrique et direction la casse !.
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[CNR] CNRS Le journal, Les défis de la voiture à hydrogène.
[ECO] Ecoconso, Voiture électrique : ses avantages et inconvénients.
[EDM] Les éditions du moteur, Voiture électrique : Le désamour inattendu qui touche 30 % des propriétaires.
[EUR] EUR-Lex, Règlement (UE) 2023/851 du Parlement européen et du Conseil du 19 avril 2023 modifiant le règlement (UE) 2019/631 en ce qui concerne le renforcement des normes de performance en matière d'émissions de CO2 pour les voitures particulières neuves et les véhicules utilitaires légers neufs conformément à l'ambition accrue de l'Union en matière de climat.
[MAC] Machines Production, Voitures électriques : l'épineux problème des batteries après un accident.
[NUM] Numerama, Au moindre accident votre voiture électrique peut finir au rebut à cause de sa batterie.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[PRE] Pressecitron, Une voiture électrique coûte-t-elle vraiment moins cher à l'usage qu'une thermique ?.
[QUE] Que choisir, Comment choisir une voiture hybride.

D7.1. Introduction :
La physique quantique est une branche fondamentale de la physique qui décrit l'univers à l'échelle microscopique au niveau des atomes, des molécules et des particules élémentaires, en tenant compte de leur nature duale d'onde et de particule.
Elle se distingue de la physique classique par des concepts contre-intuitifs tels que la quantification de l'énergie, la dualité onde-corpuscule, la superposition des états, l'indéterminisme quantique et la non-localité quantique.
Ces concepts ont donné naissance à de nombreuses technologies modernes telles que l'électronique, les ordinateurs quantiques, l'imagerie médicale et la nanotechnologie.
Albert Einstein a joué un rôle majeur dans le développement de la physique quantique, notamment par l'explication de l'effet photoélectrique (1905), la quantification des oscillateurs atomiques (1907), la dualité onde-corpuscule pour la lumière (1909), l'émission stimulée (1917) et le paradoxe EPR (1935).
Bien qu'il ait toujours reconnu la validité et l'efficacité du formalisme quantique, il s'opposait toutefois à l'interprétation probabiliste de Niels Bohr et de l'école de Copenhague. Einstein défendait une vision à la fois déterministe et locale du monde quantique, croyant en l'existence de "variables cachées" qui pourraient expliquer les phénomènes quantiques de manière plus complète.
Cependant, les expériences ultérieures, notamment celles de Alain Aspect en 1982 [ASP], ont contredit cette vision en démontrant que la mécanique quantique viole la localité quantique indépendamment de son caractère déterministe ou non.
La mécanique quantique constitue le socle théorique et mathématique qui formalise les principes fondamentaux régissant la physique quantique.
D7.2. Modèle standard de la physique des particules (rappel) :
Voir sujet Relativité - Lexique : Modèle standard de la physique des particules.
D7.3. Principes fondamentaux :
Les principes fondamentaux régissant la physique quantique sont les suivants [CHA][PER], listés par ordre chronologique de découverte.
1. Quantification de l'énergie (Max Planck, 1900, Albert Einstein, 1905-1917)
L'énergie ne peut prendre que des valeurs discrètes, appelées quanta, et non des valeurs continues.
Ce principe a été progressivement établi et étendu comme suit :
- Rayonnement du corps noir (Max Planck, 1900, et prix Nobel de physique en 1918) : pour un atome, la différence d'énergie E entre deux niveaux d'énergie est donnée par : ΔE = h ν, où h est la constante de Planck et ν la fréquence associée à la transition.
- Effet photoélectrique (Albert Einstein, 1905, et prix Nobel de physique en 1921) : Einstein étend la quantification de Planck à la lumière elle-même.
- Quantification des oscillateurs atomiques (Albert Einstein, 1907) : Einstein applique la quantification aux vibrations des atomes dans un solide.
- Emission stimulée (Albert Einstein, 1917) : Einstein complète la description de l'interaction entre lumière et matière dans laquelle un photon incident provoque la désexcitation d'un atome, émettant un second photon de mêmes direction, fréquence et polarisation.
Confirmation de la quantification introduite par Planck (1900) : expérience de Franck et Hertz (1914) qui a montré que les électrons accélérés perdaient de l'énergie par quantités discrètes lors de collisions avec des atomes de mercure.
2. Dualité onde-corpuscule (Albert Einstein, 1909, Louis de Broglie, 1924)
Les objets quantiques, comme les électrons et les photons, présentent à la fois des propriétés corpusculaires et ondulatoires selon les conditions expérimentales.
La longueur d'onde λ associée à une particule de quantité de mouvement p est donnée par : λ = h/p
Pour une particule non relativiste de masse m et de vitesse v, on a : p = m v.
Pour un photon d'énergie E, on a : p = E/c
Ce principe a été établi en deux étapes comme suit :
- Einstein pose les bases de la dualité onde-corpuscule pour la lumière (1909).
- De Broglie généralise ce concept à toute la matière (1924, et prix Nobel de physique en 1929).
Confirmation : expérience de Davisson-Germer (1927) qui a montré la diffraction d'électrons par un cristal de nickel, confirmant ainsi leur nature ondulatoire.
3. Statistique des bosons et des fermions (Satyendra Nath Bose et Albert Einstein, 1924, Enrico Fermi et Paul Dirac, 1926)
Les bosons (de spin entier, comme le photon) suivent les statistiques de Bose-Einstein quant à leur comportement collectif.
Les fermions (de spin demi-entier, comme l'électron) suivent les statistiques de Fermi-Dirac quant à leur comportement collectif.
Confirmations :
- Condensat de Bose-Einstein (Eric Cornell et Carl Wieman, 1995, et prix Nobel de physique 2001) par refroidissement des atomes de rubidium (bosons).
- Blocage de Pauli (MIT, 2021) par refroidissement d'un nuage de gaz de lithium-6 (fermions).
4. Exclusion de Pauli (Wolfgang Pauli, 1925, et prix Nobel de Physique en 1945)
Deux fermions identiques, comme les électrons, protons ou neutrons, ne peuvent pas occuper simultanément le même état quantique dans un même système.
Ce principe est fondamental pour expliquer la structure électronique des atomes, en particulier la répartition des électrons dans les couches et sous-couches atomiques, ce qui conduit à la structure du tableau périodique des éléments.
Confirmations :
- Analyse de l'effet Zeeman (1927-1930).
- Etude de la structure des bandes électroniques et physique nucléaire (1930-1940).
5. Superposition quantique (collectif, 1926)
Un système quantique existe dans un état global indéterminé sous forme d'une superposition de plusieurs états simultanément jusqu'à ce qu'une mesure soit effectuée. Après la mesure, le système s'effondre dans un état unique correspondant au résultat observé.
Confirmation : expérience de Clinton Davisson et Lester Germer (1927) portant sur la diffraction d'électrons par un cristal.
|
Formalisation [PER][CHA] : Elle s'applique à tout phénomème quantique, comme l'expérience de Stern-Gerlach (voir ci-après) pour le cas discret et le calcul avec méthode Schrödinger continue dans le cas continu. La fonction d'onde Ψ(x, t) est une représentation abstraite contenant toutes les informations possibles sur l'état d'une particule ou d'un système quantique à un instant donné. Elle permet de calculer les probabilités des différents résultats des mesures mais ne détermine pas avec certitude la résultat d'une mesure unique. Elle s'exprime mathématiquement de façon standard comme la superposition d'états propres Ψj sous la forme : - Cas discret : Ψ(x, t) = ∑j [cj Ψj(x, t)] où j est l'indice qui numérote les différents états propres Ψj - Cas continu : Ψ(x, t) = ∫R [c(k) Ψk(x, t) dk] où k est une variable continue. où la variable x peut être une position, un volume, une quantité de mouvement, une énergie, etc. Compte tenu de la condition de normalisation (voir ci-après), l'unité de Ψ(x, t) est sans dimension dans le cas discret et la racine carrée de l'inverse de l'unité de x dans le cas continu (par exemple, Ψ(x,t) a l'unité de m-1/2 pour x exprimé en mètre). Les états propres Ψj sont des modes caractéristiques du système pour lesquels la mesure d'un observable donne toujours le même résultat avec une probabilité de 100 %. Ces modes sont analogues : - Cas discret : aux fréquences spécifiques de réglage d'une radio, où l'observable est la fréquence radio, - Cas continu : aux modes de vibration spécifiques d'une corde tendue, où l'observable est la fréquence de vibration. Chaque état propre Ψj(x, t) s'exprime sous la forme complexe : Ψj(x) e-i Ej t/h' avec une partie non temporelle Ψj(x) solution de l'équation de Schrödinger stationnaire et une partie phase dépendant du temps t. Ej est l'énergie associée à l'état propre Ψj et h' la constante de Planck réduite. Les coefficients cj sont les amplitudes de probabilité associées à chaque état propre Ψj. Ils s'expriment sous la forme complexe : |cj| ei θj où |cj| est le module du coefficient et θj l'angle de phase initiale dans le plan complexe. La détermination des coefficients cj est essentiellement expérimentale. Les modules |cj| sont obtenus par des mesures statistiques sur de nombreuses copies du système. Les phases relatives nécessitent des techniques plus avancées comme la tomographie quantique. Plus généralement, quel que soit le type d'état quantique (propre ou superposé), l'amplitude de probabilité est un coefficient complexe associé à chaque état propre de la fonction d'onde, permettant de calculer la probabilité d'observer un résultat spécifique lors d'une mesure. Ce concept fut introduit en 1926 par Max Born [BOU] qui montra que la fonction d'onde Ψ ne pouvait pas être interprétée directement comme une probabilité car cela violerait les règles de calcul des probabilités pour des événements composés. Il proposa que la probabilité d'observer un état donné soit donnée par le carré du module de l'amplitude de probabilité, soit |Ψ|2 D'où les quatre cas suivants : 1. Cas discret d'un état propre Ψj : l'état du système est Ψj, avec une amplitude de probabilité de 1 pour Ψj et une probabilité de 1 d'observer l'état Ψj 2. Cas continu d'un état propre Ψj : l'état du système est Ψj(x, t), avec une amplitude de probabilité Ψj(x, t) et une densité de probabilité ρ(x, t) = |Ψj(x, t)|2 donnant la probabilité de trouver au temps t la valeur x de la variable mesurée. 3. Cas discret d'une superposition d'états propres : l'état du système est une superposition Ψ(x, t) = ∑j cj Ψj(x, t), avec une amplitude de probabilité cj pour chaque état propre Ψj et une probabilité Pj = |cj|2 d'observer l'état Ψj 4. Cas continu d'une superposition d'états propres : l'état du système est une superposition Ψ(x, t) = ∫R c(k) Ψk(x, t) dk, avec une densité d'amplitude de probabilité c(k) pour chaque état propre Ψk et une densité de probabilité ρ(x, t) = |Ψ(x, t)|2 donnant la probabilité de trouver au temps t la valeur x de la variable mesurée en tenant compte des effets d'interférence quantique entre les différents états propres. A noter que l'amplitude de probabilité est la fonction d'onde elle-même uniquement dans le cas continu d'un état propre (cas 2). La condition de normalisation garantissant que la somme des probabilités est égale à 1 impose par ailleurs que : 1. Cas discret d'un état propre Ψj : ∑i |Ψj(xi)|2 = 1 où xi sont les points de discrétisation. 2. Cas continu d'un état propre Ψj : ∫R |Ψj(x, t)|2 dx = 1 3. Cas discret d'une superposition d'états propres : ∑j |cj|2 = 1 4. Cas continu d'une superposition d'états propres : ∫R |c(k)|2 dk = 1 ou ∫R |Ψ(x, t)|2 dx = 1 Exemple concret (expérience de Stern-Gerlach, 1922) : La fonction d'onde d'un atome d'argent dont le spin est dans une superposition d'états selon l'axe z, peut s'écrire : Ψ = c1 |+z> + c2 |-z> où les états propres |+z> et |-z> représentent respectivement les orientations "up" et "down" du spin selon l'axe z. Ces états propres sont aussi les vecteurs propres de l'opérateur de spin Sz qui permet de mesurer la projection du moment angulaire sur l'axe z. Cet opérateur est défini par la matrice suivante : Sz = h'/2 (1 0) (0 -1) où h' est la constante de Planck réduite. Les vecteurs propres associés à cette matrice sont |+z> = (1, 0)T pour la valeur propre +h'/2 (spin "up"), et |-z> = (0, 1)T pour la valeur propre -h'/2 (spin "down"). Ces valeurs propres traduisent la quantification des projections du moment angulaire sur l'axe z, exprimées en unités de h' Les coefficients complexes c1 = 1/(21/2) et c2 = i/(21/2) sont les amplitudes de probabilité, tenant compte à la fois des modules et de la phase relative entre les deux états propres. Par conséquent, si l'on effectue une mesure du spin sur l'axe z, il y a 50 % de chances (= |c1|2) d'obtenir la valeur + h'/2 (état "up") et 50 % de chances (= |c2|2) d'obtenir la valeur -h'/2 (état "down"). |
6. Indéterminisme quantique (Max Born, 1926, et prix Nobel de Physique en 1954)
Les résultats des mesures ne sont pas déterministes, mais probabilistes, lorsque le système évolue librement entre les mesures ou est réinitialisé à son état initial avant chaque nouvelle expérience.
En revanche, des mesures répétées dans les mêmes conditions expérimentales, à très court intervalle, donnent le même résultat car le système reste dans l'état mesuré après la première observation.
Confirmation : expériences répétées sur les fentes de Young.
Interprétations :
- Dans l'interprétation de Copenhague (Bohr, Heisenberg), ce principe remet en question l'idée que les propriétés d'un système quantique ont une réalité objective indépendante de la mesure.
- Mais d'autres interprétations, comme celle de De Broglie-Bohm (théorie à variables cachées) ou celle de Everet (mondes multiples), contestent cette idée tout en restant compatibles avec les prédictions expérimentales. Pour ce faire, l'interprétation de De Broglie-Bohm préserve le déterminisme tout en acceptant le principe de non-localité quantique, et l'interprétation de Everett évite le problème de la non-localité en proposant que tous les résultats possibles d'une mesure se produisent simultanément dans des branches d'univers distinctes.
7. Incertitude quantique (Werner Heisenberg, 1927, et prix Nobel de Physique en 1932)
Il existe une limite fondamentale à la précision avec laquelle certaines paires de grandeurs physiques peuvent être mesurées, notamment position et quantité de mouvement, énergie et temps, spin et orientation.
Par exemple, la relation liant les incertitudes entre position (x) et quantité de mouvement (p) est donnée par :
Δx Δp ≥ h'/2
où h' est la constante de Planck réduite.
Confirmation indirecte : expérience de Davisson-Germer (1927) portant sur la diffraction d'électrons par un cristal de nickel.
8. Effet tunnel (George Gamow, 1928)
Une particule peut traverser une barrière énergétique même sans l'énergie suffisante classiquement requise. La fonction d'onde de la particule ne s'annule pas au niveau de la barrière mais s'atténue à l'intérieur de celle-ci, permettant une probabilité non nulle de la traverser.
Confirmation : expérience de George Gamow (1928) portant sur la désintégration alpha des noyaux radioactifs.
9. Intrication quantique (paradoxe EPR, par Albert Einstein, Boris Podolsky, Nathan Rosen, 1935)
Deux particules sont dites intriquées lorsqu'elles forment un système quantique global tel que la mesure de l'état de l'une détermine instantanément l'état de l'autre, quelle que soit la distance qui les sépare.
Ces corrélations quantiques instantanées ne constituent pas une transmission de signal, échappant ainsi au cadre de causalité relativiste sans le contredire.
Confirmation : expériences de Alain Aspect (1982, et prix Nobel de physique 2022) qui ont confirmé les prédictions de la mécanique quantique en violation des inégalités de Bell, confirmant ainsi l'intrication quantique [ASP].
10. Intégrale de chemin (Richard Feynman, 1948)
Une particule allant d'un point à un autre emprunte simultanément tous les chemins possibles pour arriver à destination. Chaque chemin est associé à une amplitude complexe (module et phase) et le probabilité de trouver la particule à un endroit donné est déterminée par la somme des amplitudes de toutes les trajectoires possibles.
Cette approche est une reformulation élégante et puissante de l'équation de Schrödinger.
Confirmation : expérience de Hitachi (1989) portant sur l'interférence d'électrons uniques.
11. Décohérence quantique (David Bohm, 1951)
Un système quantique peut perdre sa cohérence (superposition d'états) en interagissant avec son environnement, conduisant à un comportement apparemment classique.
Confirmation : expériences montrant la transition quantique-classique (Serge Haroche, 1996, Anton Zeilinger, 2003).
12. Non-localité quantique (théorème de Bell, par John Bell, 1964)
Les objets quantiques peuvent présenter des corrélations instantanées à distance. La non-localité englobe l'intrication quantique en incluant des corrélations dans le temps, des systèmes multi-particules complexes, des interactions entre particules et objets macroscopiques, des phénomènes délocalisés sans nécessiter d'interaction directe.
Confirmation : expériences de Alain Aspect (1982) qui ont confirmé les prédictions de la mécanique quantique en violation des inégalités de Bell, confirmant ainsi la non-localité [ASP].
13. Théorie quantique des champs (collectif)
La théorie quantique des champs (TQC) est un cadre théorique unifiant mécanique quantique et relativité restreinte. Elle modélise les particules comme des excitations localisées de champs quantiques qui remplissent tout l'espace-temps, permettant notamment d'expliquer la création et l'annihilation de particules.
Seule l'intrication quantique échappe à l'interprétation de la causalité par son caractère non-local et l'absence de transmission de signal, tout en restant compatible avec le formalisme de la relativité restreinte.
On peut citer les contributions suivantes :
- Théorie quantique du champ électromagnétique (Paul Dirac, 1927) confirmé en 1930 par l'analyse des spectres atomiques (notamment Alfred Lande et Otto Stern).
- Electrodynamique quantique (QED) décrivant l'interaction entre la lumière et la matière (Richard Feynman, Julian Schwinger, Sin-Itiro Tomonaga, Freeman Dyson, 1940, et prix Nobel de physique en 1965), confirmée en 1947 par Polykarp Kusch et Henry Foley par des expériences sur le moment magnétique de l'électron.
- Théories de jauge non abéliennes (Yang Chen-Ning et Robert Mills, 1954) donnant un cadre théorique pour décrire les interactions non abéliennes comme l'interaction faible et forte.
- Unification de l'électromagnétisme et de l'interaction faible dans un modèle standard (Steven Weinberg, Abdus Salam, Sheldon Glashow, 1960, et prix Nobel de physique 1979), confirmée en 1983 au CERN par la découverte des bosons W+, W- et Z0.
- Boson de Higgs (Peter Higgs et François Englert, 1964, et prix Nobel de physique 2013) confirmé en 2012 au CERN par les expériences ATLAS et CMS du LHC (Grand collisionneur de hadrons).
- Chromodynamique quantique (QCD) décrivant l'interaction forte entre quarks et gluons (David Gross, Frank Wilczek, David Politzer, 1973, et prix Nobel de physique 2004, Kenneth G. Wilson, 1974), confirmée en 1979 au centre DESY (Deutsches Elektron SYnchrotron) par l'observation des jets hadroniques issus de collisions de particules à haute énergie.
D7.4. Etat quantique :
L'état quantique d'une particule élémentaire est une description mathématique complète de ses aspects observables et probabilistes, distincte de ses propriétés intrinsèques.
Il s'étend également aux systèmes composés où les interactions, les corrélations et les phénomènes d'intrication entre particules jouent un rôle fondamental.
Il se formalise par un vecteur d'état |Ψ> dans un espace abstrait de Hilbert, associé à une fonction d'onde Ψ(x,t) dans une base concrète, généralement celle des positions ou des quantités de mouvement.
Les propriétés intrinsèques sont des caractéristiques invariantes qui définissent la nature fondamentale de la particule, en particulier la masse m et les nombres quantiques intrinsèques.
Les observables sont des grandeurs physiques mesurables (comme la position x ou la quantité de mouvement p) représentés mathématiquement par des opérateurs hermitiens (comme X ou P).
- Avant mesure, l'observable est une prédiction statistique obtenue en calculant la moyenne pondérée des résultats possibles de la mesure, les poids étant déterminés par les probabilités associées à l'état quantique initial du système.
- Après mesure, un observable fournit une valeur qui correspond à l'une des valeurs propres de l'opérateur associé à l'observable.
Les opérateurs agissent sur l'état quantique du système (fonction d'onde ou vecteur d'état dans un espace de Hilbert) pour calculer des informations, telles que les valeurs possibles des observables (valeurs propres) et les probabilités associées à chaque résultat de mesure. Pour exemples :
- l'opérateur position X est la multiplication par x sous la forme : X(Ψ(x)) = x Ψ(x), permettant de calculer la valeur moyenne de la position pour cet état.
- l'opérateur énergie cinétique T agit sur la fonction d'onde sous la forme : T(Ψ(x)) = -h'2/(2 m) (d2Ψ(x, t)/dx2)
- l'opérateur quantité de mouvement P agit par dérivation sous la forme : P(Ψ(x)) = -i h' dΨ(x)/dx, permettant de calculer la valeur moyenne de la quantité de mouvement pour cet état.
A noter que P peut s'écrire aussi : P = -i h' d/dx
- l'opérateur hamiltonien H agit sur la fonction d'onde sous la forme : H(Ψ(x, t)) = -h'2/(2 m) (d2Ψ(x, t)/dx2) + V(x) Ψ(x, t), permettant de calculer l'énergie totale du système.
A noter que H peut s'écrire aussi : H = -h'2/(2 m) (d2/dx2) + V(X) = P2/(2 m) + V(X)
- l'opérateur moment cinétique J agit sur la fonction d'onde sous forme d'un produit vectoriel : J(Ψ(x, t)) = r x P(Ψ(x, t)), où r est le vecteur position et P l'opérateur quantifié de mouvement, permettant de calculer le moment cinétique du système.
- l'opérateur parité π agit la fonction d'onde sous la forme : π(Ψ(x)) = Ψ(-x), permettant de déterminer la symétrie de la fonction d'onde par rapport à l'inversion spatiale.
- les opérateurs d'échelle (création a+ et annihilation a) agissent sur les états quantiques en ajoutant ou retirant une particule ou un quantum d'excitation.
- l'opérateur spin S agit sur les fonctions d'onde de spin sous la forme de matrices 2x2 de Pauli, permettant de décrire le moment cinétique intrinsèque des particules. Ces matrices sont les suivantes :
σ1 = σx =
(0 1)
(1 0)
σ2 = σy =
(0 -i)
(i 0)
σ3 = σz =
(1 0)
(0 -1)
Ces matrices vérifient la propriété : σ1 σ2 σ3 = i I où I est la matrice Identité.
La valeur propre est un résultat possible et spécifique obtenu lors de la mesure d'un observable sur un système quantique. Elle est obtenue avec certitude si le système est dans un état propre correspondant, et avec une probabilité donnée si le système est dans une superposition d'états propres. Voir expérience de Stern-Gerlach.
Le vecteur propre représente l'état du système lorsque la mesure d'un observable donne une valeur propre. Voir expérience de Stern-Gerlach.
Les vecteurs propres forment une base de l'espace des états quantiques permettant de décrire toutes les configurations possibles du système.
Les probabilités de mesure décrivent comment ces observables se distribuent dans leurs domaines de valeurs possibles en termes de densité de probabilités.
Elles suivent la règle de Born selon laquelle la densité de probabilité ρ vaut |<Ψj|Ψ>|2 où Ψj est l'état propre associé à une valeur propre de l'observable mesuré, c'est-à-dire l'état dans lequel se trouve le système immédiatement après la mesure.
La notation bra-ket <.|.> désigne le produit scalaire hermitien qui généralise le produit scalaire classique aux espaces vectoriels complexes sous la forme :
< u|v > = v+.u
où :
u et v = deux vecteurs colonnes quelconques
v+ = adjoint de v = conjugué complexe transposé tel que v+ = (v*)T
* = opérateur conjugué complexe sans transposition
Exemple : si u = (1 + 2 i, 3)T et v = (4 + 5 i, 6 i)T, alors v* = (4 - 5 i, -6 i)T, v+ = (v*)T = (4 - 5 i, -6 i) et < u|v > = v+.u = (4 - 5 i)(1 + 2 i) + (-6 i)(3) = 14 - 15 i
Exemples de particules élémentaires avec distinction intrinsèque/observable :
Caractéristiques de l'Electron e- :
| Classification : Lepton
| Composition : N/A (Particule élémentaire)
| Masse (m) = 0,511 MeV/c2
| Moment magnétique intrinsèque (μ) = -9,284 10-24 J/T
| Chiralité = Droite et Gauche (mélange possible)
| Symétrie CPT (Charge, Parité, Temps) : Oui
| Interactions fondamentales : forces électromagnétique, faible et gravitationnelle
| Durée de vie (τ) = parfaitement stable (6,6 1028 années)
| Anti-particule : positron
| Nombres quantiques intrinsèques :
| | Spin (S) = 1/2
| | Isospin (T3) = -1/2 (pour l'isospin faible)
| | Charge électrique (Q) = -1e
| | Charge de couleur : N/A (particule autre que Quark et Gluon)
| | Saveur (Le) = électronique
| | Nombre leptonique (L) = +1
| | Nombre baryonique (B) = 0
| Nombres quantiques observables :
| | Nombre quantique principal (n) = entier strictement positif
| | Nombre quantique secondaire ou azimutal (l) = entier de 0 à n - 1
| | Nombre quantique magnétique (ml) = entier de -l à +l
| | Nombre quantique magnétique de spin ou projection de spin (ms) = +1/2 ("up") ou -1/2 ("down")
| | Nombre quantique de moment angulaire total (j) = |l ± s|
| | Nombre quantique ou projection du moment angulaire total (mj) = de -j à +j par pas entiers
| | Projection du moment magnétique (μz) = ±9,284 10-24 J/T
| | Parité (P) = selon contexte
| | Position, quantité de mouvement et énergie totale
Caractéristiques du Positron e+ = Anti-électron :
| Classification : Anti-Lepton
| Composition : N/A (Particule élémentaire)
| Masse (m) = 0,511 MeV/c2
| Moment magnétique intrinsèque (μ) = +9,284 10-24 J/T
| Chiralité = Gauche et Droite (mélange possible)
| Symétrie CPT (Charge, Parité, Temps) : Oui
| Interactions fondamentales : forces électromagnétique, faible et gravitationnelle
| Durée de vie (τ) = parfaitement stable en isolation et courte en présence de matière
| Anti-particule : électron
| Nombres quantiques intrinsèques :
| | Spin (S) = 1/2
| | Isospin (T3) = +1/2 (pour l'isospin faible)
| | Charge électrique (Q) = +1e
| | Charge de couleur : N/A (particule autre que Quark et Gluon)
| | Saveur (Le) = électronique
| | Nombre leptonique (L) = -1
| | Nombre baryonique (B) = 0
| Nombres quantiques observables :
| | Nombre quantique principal (n) = entier strictement positif
| | Nombre quantique secondaire ou azimutal (l) = entier de 0 à n - 1
| | Nombre quantique magnétique (ml) = entier de -l à +l
| | Nombre quantique magnétique de spin ou projection de spin (ms) = +1/2 ("up") ou -1/2 ("down")
| | Nombre quantique de moment angulaire total (j) = |l ± s|
| | Nombre quantique ou projection du moment angulaire total (mj) = de -j à +j par pas entiers
| | Projection du moment magnétique (μz) = ±9,284 10-24 J/T
| | Parité (P) = selon contexte
| | Position, quantité de mouvement et énergie totale
D7.5. Méthodes de calcul quantique :
Toutes les méthodes de calcul quantique ont pour objet de calculer les valeurs possibles des observables et leurs probabilités de mesure, mais elles le font de manières différentes selon les domaines d'application.
Attention : il est courant d'omettre dans les équations certaines constantes universelles, notamment la constante de Planck (h), la constante de Planck réduite (h'), la vitesse de la lumière (c), la matrice Identité (I) et la constante gravitationnelle (G).
Parmi les méthodes de calcul, on peut citer :
D7.5.1. Méthode non-relativistes de type Schrödinger :
Ces approches étudient l'évolution temporelle de l'état quantique |Ψ> (i.e. fonction d'onde Ψ(x, t)), tandis que les observables restent fixes sauf si le potentiel V(x, t) dépend explicitement du temps.
Elles sont utilisées notamment en chimie quantique et suivent l'équation de Schrödinger (1926, et prix Nobel de Physique 1933).
En particulier, pour une particule sans spin de masse m, se déplaçant dans un espace unidimensionnel et soumise à un potentiel V(x), cette équation s'écrit sous la forme :
(L1) i h' dΨ(x, t)/dt = -(1/2)(h'2/m)(d2Ψ(x, t)/dx2) + V(x) Ψ(x, t)
où h' est la constante de Planck réduite (ou constante de Dirac = h' = h/(2 π))
et h est la constante de Planck (h = 6,626 10-34 J.s).
Voir exemple de calcul avec méthode Schrödinger continue et exemple de calcul avec méthode Schrödinger discrétisée.
D7.5.2. Méthodes relativistes de type Schrödinger :
L'évolution temporelle de l'état quantique est décrite par des équations d'onde généralisant l'équation de Schrödinger pour des particules se déplaçant à des vitesses proches de celle de la lumière. On peut citer :
1. Equation de Dirac pour les particules relativistes de spin 1/2 (exemples : électron, neutrino).
En particulier, pour une particule libre, cette équation s'écrit :
(D1) (i h' γμ dμ - m c I) Ψ = 0
où :
Ψ est la fonction d'onde de Dirac à quatre composantes, appelée spineur, qui encode simultanément les deux états propres du spin ("up"/"down"), les solutions d'énergie positive/négative (particule/anti-particule) et leur couplage relativiste, comme suit :
- Lorsque la quantité de mouvement p est nulle, les quatre composantes se décomposent en deux paires distinctes. La première (Φ) encode les amplitudes de probabilité associées aux états propres du spin de la particule (exemple : électron). La seconde (Χ) encode celles de l'antiparticule correspondante (exemple : positron).
- Dès que p ≠ 0, les quatre composantes décrivent soit une particule (énergie positive), soit une antiparticule (énergie négative). Chaque solution individuelle reste un état à quatre composantes où le spin (décrit par les matrices de Pauli σ) et la quantité de mouvement (vecteur p) sont couplés. L'une des paires encode les états propres du spin hérités du référentiel au repos, modulés par le mouvement. L'autre paire encode leur modification relativiste en reliant les deux paires via l'énergie totale E.
m est la masse de la particule au repos.
I est la matrice Identité 4x4
γμ sont des matrices 4x4 spécifiques introduites par Dirac, l'indice μ variant de 0 à 3 (0 correspondant au temps). Ces matrices sont les suivantes en représentation standard Pauli-Dirac :
γ0 =
(I 0)
(0 -I)
γi =
(0 σi)
(-σi 0)
γ5 = i γ0 γ1 γ2 γ3
(0 I)
(I 0)
dans lesquelles σi sont les matrices 2x2 de Pauli et I est la matrice Identité 2x2.
Les matrices γμ satisfont à la relation d'anticommutation du groupe de Lorentz : {γμ, γν} = γμ γν + γν γμ = 2 gμν I avec gμν = métrique de Minkowski et I = matrice Identité 4x4.
dμ sont les dérivées partielles par rapport aux coordonnées xμ = (ct, x1, x2, x3) dans l'espace-temps de Minkowski.
γμ dμ implique une sommation sur l'indice μ conformément à la convention de sommation d'Einstein.
L'équation de Dirac relie donc les propriétés dynamiques de la particule (énergie et quantité de mouvement via l'opérateur différentiel i h' γμ dμ) à sa masse propre m.
Voir exemple de calcul avec méthode Dirac.
2. Equation de Klein-Gordon pour les particules relativistes de spin
0
(exemple : boson de Higgs).
3. Equation de Proca pour les particules relativistes de spin
1
(exemples : photon, bosons W et Z).
4.
Equation de Rarita-Schwinger pour les particules relativistes de spin 3/2
(exemple : gravitino).
5. Généralisations des équations de Rarita-Schwinger pour les particules relativistes de spin demi-entier supérieur à 3/2.
6. Equations d'Einstein linéarisées pour le graviton sans masse de spin 2.
Toutes ces équations sont invariantes par transformation de Lorentz-Poincaré, ce qui les rend compatibles avec la relativité restreinte.
Cependant, l'interprétation de ces équations dans le cadre d'une théorie à une seule particule conduit à certaines incohérences.
C'est pourquoi la Théorie quantique des champs s'impose comme un cadre plus général et cohérent.
D7.5.3. Méthodes de type Heisenberg :
Ces approches étudient l'évolution temporelle des observables, tandis que l'état quantique reste fixe.
Elles sont utilisées notamment en calculs d'opérateurs quantiques et Théorie quantique des champs. Elles suivent l'équation de Heisenberg :
(H1) dA/dt = (i/h') [H, A] + DA/Dt
où :
A est l'opérateur A(t) qui représente l'observable à étudier (par exemple la position x(t) ou la quantité de mouvement p(t))
H est l'opérateur hamiltonien du système
[H, A] est le commutateur entre H et A, défini par : [H, A] = H A - A H
DA/Dt est la dérivée explicite de l'opérateur A en représentation de Schrödinger, obtenue en dérivant uniquement sa partie temporelle. Par exemple si A(t) = cos(ω t) X alors DA/Dt = -ω sin(ω t) X
Voir exemple de calcul avec méthode Heisenberg.
D7.5.4. Méthodes de type Dirac :
Ces approches combinent l'évolution temporelle de l'état quantique et des observables en décrivant les interactions entre particules relativistes dans le cadre de la théorie quantique des champs, notamment en électrodynamique quantique à travers les calculs perturbatifs et les diagrammes de Feynman.
Ces approches utilisent une version élargie de l'équation relativiste de Dirac pour particule libre de spin 1/2.
D7.5.5. Méthodes algébriques avancées :
Ces méthodes générales, basées sur des outils algébriques (matrices, opérateurs, algèbres de Lie), sont utilisées lorsqu'il est difficile, voire impossible, de résoudre exactement les équations de mouvement, qu'elles soient différentielles (type Schrödinger), matricielles (type Heisenberg) ou interactionnelles (type Dirac).
Elle permettent la résolution de systèmes simples (atome, petites molécules) ou plus complexes (grandes molécules, matériaux) en fournissant des solutions exactes ou approximatives.
On peut citer :
- la théorie des perturbations qui est utilisée lorsque le système peut être considéré comme une modification d'un cas soluble.
- la méthode variationnelle qui fournit une estimation des énergies des états liés en minimisant une fonction d'essai.
- les approches ab initio qui résolvent approximativement l'équation de Schrödinger à partir des principes fondamentaux, sans recourir à des paramètres empiriques.
D7.5.6. Méthodes numériques :
Ces méthodes sont utilisées lorsqu'il est impossible d'obtenir les solutions analytiques des équations.
On peut citer : méthode de Monte-Carlo, méthode des différences finies, méthode de Lanczos.
D7.6. Exemple de calcul avec méthode Schrödinger continue :
L'exemple suivant illustre les calculs quantiques en utilisant l'équation de Schrödinger.
Hypothèses :
On considère une particule libre, non relativiste, massique et sans spin, située dans un puits de potentiel infini unidimensionnel.
L'évolution temporelle de la fonction d'onde Ψ est alors donnée par l'équation de Schrödinger (relation L1).
(L1) i h' dΨ(x, t)/dt = -(1/2)(h'2/m)(d2Ψ(x, t)/dx2) + V(x) Ψ(x, t)
Dans le cas ou l'on cherche les états propres Ψj du système (numérotés par l'indice j), la fonction d'onde Ψj(x,t) peut se décomposer en une partie spatiale stationnaire et une partie temporelle oscillante, sous la forme :
(L2) Ψj(x,t) = Ψj(x) T(t)
La relation (L1) devient alors :
(L3) i h' (1/T) dT/dt = -(1/2)(h'2/m) (1/Ψj(x)) (d2Ψj(x)/dx2) + V(x)
Puisque le membre de gauche dépend uniquement de t et celui de droite uniquement de x, ils sont égaux à une constante Ej (l'énergie totale de la particule dans l'état propre Ψj).
Equation spatiale :
En conséquence, la relation (L3) devient :
(S1) -(1/2)(h'2/m) (d2Ψj(x)/dx2) + V(x) Ψj(x) = Ej Ψj(x)
Si le puits de potentiel infini est de largeur L, on a de plus :
(S2) V(x) = 0 pour 0 < x < L et V(x) = ∞ pour x ≤ 0 ou x ≥ L
A l'intérieur du puits, l'équation (S1) devient alors :
(S3) d2Ψj(x)/dx2 + kj2 Ψj(x) = 0
avec : kj = (2 m Ej)1/2 / h'
La solution générale est donc :
(S4) Ψj(x) = A sin(kj x) + B cos(kj x)
où A et B sont des constantes arbitraires.
Pour x = 0, Ψj(x) = 0 d'où B = 0
Pour x = L, Ψj(x) = 0 d'où A sin(kj L) = 0 qui nécessite d'avoir des valeurs discrètes pour kj et Ej telles que :
(S5) kj = j π/L
(S6) Ej = (1/2)(h' kj)2 /m = (1/2)(j π h'/L)2 /m
avec j entier positif non nul (Ψj ne pouvant pas être nulle partout dans le puits).
Finalement, on obtient :
(S7) Ψj(x) = A sin(j π x/L)
Il reste à calculer A en tenant compte de la condition de normalisation de Ψj(x, t) :
(S8) ∫0 à L [|Ψj(x)|2 dx] = 1
Compte tenu de la relation (S7) et de l'identité trigonométrique : sin2(θ) = (1/2) (1 - cos(2 θ)), on obtient alors :
1 = ∫0 à L [(1/2) A2 (1 - cos(2 j π x/L)) dx] = (1/2) A2 (∫0 à L [dx] - ∫0 à L [cos(2 j π x/L) dx])
La première intégrale vaut [x]0 à L = L
La seconde intégrale vaut (L/(2 j π)) [sin(2 j π x/L)]0 à L = 0
D'où : A = ±(2/L)1/2
On prend par convention la valeur positive de A car une fonction d'onde peut toujours être multipliée par un facteur de phase globale (comme -1 ou même eiθ) sans changer les prédictions physiques.
La relation (S7) devient alors :
(S9) Ψj(x) = (2/L)1/2 sin(j π x/L) avec j entier positif non nul
Equation temporelle :
compte tenu de la constante Ej, la relation (L3) devient :
(T1) dT(t)/dt + i Qj T(t) = 0
avec :
(T2) Qj = Ej/h' = (j π/L)2 h'/(2 m)
qui admet comme solution :
(T3) T(t) = Cj e-i Qj t
avec Cj constante complexe arbitraire qui vaut n'importe quel facteur de phase de module 1 (Cj = ei θj avec θj nombre réel) afin de respecter la condition de normalisation de Ψj(x, t) (relation S8).
Pour simplifier les calculs, on prend conventionnellement Cj = 1. Mais ce choix est arbitraire et doit être revu si des interférences ou des superpositions d'états sont étudiées, car les phases relatives entre différents états jouent un rôle crucial dans ces situations.
Fonction d'onde complète :
compte tenu des relations (L2)(S9)(T3), la fonction d'onde normalisée complète est donc :
(C1) pour 0 < x < L : Ψj(x,t) = Ψj(x) T(t) = (2/L)1/2 sin(j π x/L) ei θj e-i Qj t avec j entier positif non nul ; sinon : Ψj(x,t) = 0
Pour toute valeur de j, il y a toujours deux noeuds aux extrémités du puits (x = 0 et x = L) et (j - 1) noeuds additionnels à l'intérieur du puits.
L'état fondamental (j = 1) correspond à : Ψ1(x,t) = (2/L)1/2 sin(π x/L) ei θ1 e-i Q1 t avec deux noeuds aux extrémités du puits.
Le premier état excité (j = 2) correspond à : Ψ2(x,t) = (2/L)1/2 sin(2 π x/L) ei θ2 e-i Q2 t avec un noeud additionnel.
etc.
Amplitudes de probabilité :
La densité ρ de probabilité s'écrit alors :
(D1) ρ = |Ψj(x,t)|2 = (2/L) sin2(j π x/L)
A noter que cette densité de probabilité est indépendante du temps, ce qui caractérise un état stationnaire.
Mesures de l'observable :
compte tenu de la relation (T2), l'énergie Ej de la particule dans l'état propre Ψj(x) s'écrit :
(O1) Ej = (j π h'/L)2/(2 m) = (j h/L)2/(8 m) avec j entier positif non nul
En conclusion :
- Si la particule est dans un état propre Ψj(x), son énergie mesurée sera toujours Ej.
- Si la particule est dans une superposition d'états propres Ψ(x) = ∑j [cj Ψj(x)], son énergie mesurée sera Ej avec une probabilité |cj|2 où cj est le coefficient de la superposition.
D7.7. Exemple de calcul avec méthode Schrödinger discrétisée :
L'exemple suivant est le même que le précédent en supposant que la fonction d'onde Ψ(x) est discrétisée sur un ensemble de N points {x1, ..., xi, ..., xN} intérieurs à l'intervalle [0, L].
Equation de Schrödinger discrétisée :
Soit j l'indice qui numérote les différents états propres Ψj du système quantique.
Attention à ne pas confondre les indices i et j : l'indice j, bien que limité à N dans cette représentation discrétisée, n'est pas intrinsèquement lié à l'indice i des points de discrétisation spatiale et pourrait, en principe, s'étendre à l'infini dans un système quantique continu. Cette distinction est fondamentale pour éviter toute confusion entre la nature physique des états quantiques (indexés par j) et leur représentation numérique discrète (indexée par i).
Le développement de Taylor à l'ordre 2 de Ψj(xi+1) et de Ψj(xi-1) s'écrit :
Ψj(xi+1) = Ψj(xi) + Δ dΨj(xi)/dx + (1/2) Δ2 d2Ψj(xi)/dx2
Ψj(xi-1) = Ψj(xi) - Δ dΨj(xi)/dx + (1/2) Δ2 d2Ψj(xi)/dx2
où Δ est l'espacement entre les points discrétisés.
En additionnant ces deux relations, on obtient la dérivée seconde d2Ψj(xi)/dx2 sous forme discrétisée comme suit :
d2Ψj(xi)/dx2 = (Ψj(xi+1) - 2 Ψj(xi) + Ψj(xi-1)) / Δ2
Dans le cas de l'exemple, cela donne :
- intervalle Δ = L/(N + 1)
- en limite gauche : Ψj(x0) = Ψj(0) = 0
- en limite droite : Ψj(xN+1) = Ψj(L) = 0
L'équation de Schrödinger (relation S1) sous forme discrétisée devient alors une équation matricielle pour tout état propre Ψj :
f H Ψj = Ej Ψj
avec :
f = facteur multiplicatif = -(h'/Δ)2/(2 m)
Ψj = vecteur colonne de composantes Ψj(xi)
Ej = énergie propre associée à l'état propre Ψj
H = matrice hermitienne =
(-2 1 0 0 ... 0 0 0)
( 1 -2 1 0 ... 0 0 0)
( 0 1 -2 1 ... 0 0 0)
( 0 0 1 -2 ... 0 0 0)
( . . . . . . .)
( 0 0 0 0 ... -2 1 0)
( 0 0 0 0 ... 1 -2 1)
( 0 0 0 0 ... 0 1 -2)
Il reste maintenant à trouver les N valeurs propres λj de la matrice H et les N vecteurs propres Ψj associés. Deux méthodes existent :
Résolution par diagonalisation de H :
Elle consiste à trouver, généralement par des méthodes numériques, deux matrices D et P tel que : H = P D P-1
dans laquelle :
- D est une matrice diagonale qui contient sur sa diagonale les valeurs propres de H
- P est une matrice dont les colonnes sont les vecteurs propres associés aux valeurs propres
- P-1 est la matrice inverse de P
- A noter que pour une matrice symétrique réelle comme H, alors P est orthogonale (P-1 = PT).
Résolution par calcul direct :
Le calcul direct des N valeurs propres λj de la matrice H, généralement par des méthodes numériques, consiste à résoudre l'équation caractéristique : det(H - λ I) = 0 où I est la matrice Identité.
Plus rapidement, la matrice H étant tridiagonale symétrique avec a = -2 sur la diagonale principale et b = 1 sur les deux diagonales secondaires, on obtient la solution : λj = a + 2 b cos(j π/(N + 1)). Voir démonstration ci-après.
Les énergies propres Ej sont alors liées aux valeurs propres λj par la relation : Ej = f λj
Ces énergies représentent les résultats possibles d'une mesure de l'énergie du système.
Le calcul direct des N vecteurs propres Ψj consiste ensuite à résoudre le système : (H - λ I) Ψj = 0, par exemple par la méthode de Gauss.
Plus rapidement, la matrice H étant tridiagonale symétrique, les composantes i du jième vecteur propre normalisé est donné par : Ψji = (2/(N + 1))1/2 sin(j i π/(N + 1)). Voir démonstration ci-après.
Ces vecteurs propres décrivent les états propres de la particule, chaque vecteur propre représentant la distribution spatiale de probabilité de la particule pour l'énergie correspondante. Cela signifie que |Ψji|2 = (2/(N + 1)) sin2(j i π/(N + 1)) donne la probabilité de trouver la particule en position xi pour l'état d'énergie Ej.
La condition de normalisation : ∑i |Ψji|2 = 1 pour chaque état propre Ψj se trouve alors automatiquement vérifiée.
Comparaison avec la solution du cas continu :
En remplaçant i par x/Δ = x (N + 1)/L dans l'expression de Ψji, on obtient :
Ψj(x) = (2/(N + 1))1/2 sin(j π x/L)
qui est équivalent à la partie spatiale de Ψj(x,t) dans la relation C1 à un facteur de normalisation près ((2/(N + 1))1/2 au lieu de (2/L)1/2).
Cette différence reflète la nature différente de la normalisation portant sur une densité de probabilité dans le cas continu, et sur des probabilités ponctuelles dans le cas discret.
Concernant l'énergie Ej, elle s'écrit : Ej = f λj = f (-2 + 2 cos(j π/(N + 1)))
Quand N est grand, compte tenu du développement limité du cosinus autour de 0 : cos(α) = 1 - (1/2)α2 + o(α2), l'expression Ej devient : Ej = -f (j π/(N + 1))2
compte tenu de Δ = L/(N + 1), on a par ailleurs : f = -(h'/Δ)2/(2 m) = -(h' (N + 1)/L)2/(2 m)
En remplaçant f dans Ej, on trouve alors : Ej = (j π h'/L)2/(2 m) qui est équivalent à l'énergie Ej du cas continu (relation O1).
Ces deux équivalences montrent la cohérence entre les approches continue et discrète pour cet exemple de calcul.
Démonstration de : λj = a + 2 b cos(j π/(N + 1)) :
Pour simplifier la notation, on pose vi = Ψji
L'équation (H - λ I) Ψj = 0 donne la relation (R1) suivante pour chaque composante i telle que 2 ≤ i ≤ N - 1 :
(R1) b vi-1 + a vi + b vi+1 - λ vi = 0
On suppose la solution de la forme vi = sin(i θj) où θj est un paramètre à déterminer.
compte tenu de l'identité trigonométrique : sin((i ± 1) θj) = sin(i θj) cos(θj) ± cos(i θj) sin(θj), la relation (R1) se simplifie alors en :
(R2) λ = a + 2 b cos(θj)
Les conditions aux limites : v0 = vN + 1 = 0 donnent ensuite :
v0 = 0 = sin(0 θj), ce qui est satisfait.
vN + 1 = 0 = sin((N + 1) θj), ce qui nécessite :
(R3) θj = j π/(N + 1)
D'où la solution complète : λj = a + 2 b cos(j π/(N + 1))
Démonstration de : Ψji = (2/(N + 1))1/2 sin(j i π/(N + 1))
Soit Cj un facteur de normalisation positif tel que : Ψji = Cj sin(i θj)
La norme du vecteur Ψj doit être égale à 1, ce qui impose :
1 = ∑i Ψji2 = Cj2 ∑i sin2(i θj)
Il reste à calculer : ∑i sin2(i θj)
compte tenu de l'identité trigonométrique : sin2(α) = (1/2) (1 - cos(2 α)) et de la formule d'Euler pour l'exponentielle complexe : exp((-1)1/2 α) = cos(α) + (-1)1/2 sin(α), on obtient :
(R4) ∑i sin2(i θj) = (1/2) (N - S)
avec : S = Partie_réelle[∑i exp(2 i θj (-1)1/2)]
La somme des exponentielles forment une série géométrique de raison r = exp(2 θj (-1)1/2) et de premier terme r, ce qui s'écrit :
S = Partie_réelle[r (1 - rN)/(1 - r)]
On a par ailleurs :
r = exp(2 θj (-1)1/2) = exp(2 j π/(N + 1) (-1)1/2)
Supposons que r = 1. Cela impliquerait que son argument est un multiple entier de 2 π c'est-à-dire : 2 j π/(N + 1) = 2 k π avec k entier, soit après simplification : j = k (N + 1) ce qui impossible (vu que 0 < j < N + 1). Le dénominateur (1 - r) n'est donc jamais nul.
On a aussi :
rN = exp(2 θj (-1)1/2)N = exp((-1)1/2 2 j π N/(N + 1)) = exp((-1)1/2 2 j π (1 - 1/(N + 1)) = exp((-1)1/2 2 j π) / exp((-1)1/2 2 j π/(N + 1)) = 1/r
D'où finalement : S = Partie_réelle[-1] = -1
En reportant cette valeur dans la relation (R4), on obtient :
∑i sin2(i θj) = (1/2) (N + 1)
Cj2 = 2/(N + 1)
D'où la forme normalisée du vecteur Ψj :
Ψji = (2/(N + 1))1/2 sin(j i π/(N + 1))
D7.8. Exemple de calcul avec méthode Heisenberg :
L'exemple suivant illustre les calculs quantiques en utilisant l'équation de Heisenberg.
On considère un oscillateur harmonique quantique unidimensionnel de masse m et de fréquence angulaire ω (relative à la raideur du ressort).
L'évolution temporelle d'un observable quelconque a(t) est alors donnée par l'équation de Heisenberg (relation H1) sous la forme :
(H1) dA/dt = (i/h') [H, A] + DA/Dt
avec :
A = opérateur A(t) qui représente l'observable a(t)
X = opérateur position
P = -i h' d/dx = opérateur quantité de mouvement
(H2) H = P2/(2 m) + V(X) = hamiltonien H du système
V(X) = (1/2) m ω2 X2 = potentiel pour un oscillateur quantique harmonique
[H, A] = H A - A H = commutateur entre H et A
DA/Dt = dérivée explicite de l'opérateur A en représentation de Schrödinger
On cherche à calculer les deux opérateurs A(t) = X(t) et A(t) = P(t).
Ce sont deux opérateurs de base qui ne dépendent pas explicitement du temps dans leur définition mathématique, donc : DA/Dt = 0
Calcul de [P, X] :
[P, X] Ψ = P (X Ψ) - X (P Ψ) = -i h' d(x Ψ)/dx - x (-i h' dΨ/dx) = -i h' (Ψ + x dΨ/dx) + i h' x dΨ/dx = -i h' Ψ
donc [P, X] = -i h'
Calcul de [P2, X] :
compte tenu de la propriété des commutateurs : [AB, C] = (AB)C - C(AB) = (ABC - ACB) + (ACB - CAB) = A[B, C] + [A, C]B, on peut écrire :
(H3) [P2, X] = P[P, X] + [P, X] P = -2 i h' P
Calcul de [X2, P] :
(H4) [X2, P] = X [X, P] + [X, P] X = 2 i h' X
Calcul de [H, A] pour A = X :
compte tenu de la relation (H2), cela s'écrit :
[H, X] = (1/(2 m)) [P2, X] + (1/2) m ω2 [X2, X]
compte tenu de la relation (H3) et de la propriété [X2, X] = 0, cela s'écrit finalement :
[H, X] = -i h' P/m
Et la relation (H1) devient alors :
(H5) dX/dt = P/m
Calcul de [H, A] pour A = P :
compte tenu de la relation (H2), cela s'écrit :
[H, P] = (1/(2 m)) [P2, P] + (1/2) m ω2 [X2, P]
compte tenu de la propriété [P2, P] = 0 et de la relation (H4), cela s'écrit finalement :
[H, P] = i h' m ω2 X
Et la relation (H1) devient alors :
(H6) dP/dt = -m ω2 X
Les relations (H5)(H6) constituent un système d'équations différentielles couplées dont la solution est la suivante :
X(t) = X(0) cos(ω t) + (1 /(m ω)) P(0) sin(ω t)
P(t) = P(0) cos(ω t) - m ω X(0) sin(ω t)
Les opérateurs X et P oscillent donc de manière harmonique à la fréquence ω en fonction des conditions initiales X(0) et P(0).
A noter qu'on retrouve la relation classique P(t) = m dX(t)/dt qui est valide dans le cas de l'exemple et dans certains systèmes simples en représentation de Heisenberg, mais qui n'est pas universelle pour tous les problèmes quantiques. Cette relation est notamment valide pour tout H de la forme : P2/(2 m) + V(X) avec V(X) combinaison de termes polynomiaux (V(X) = a + b X + c X2 + ...), vu que [Xn, X] = 0 pour tout n entier positif ou nul.
D7.9. Exemple de calcul avec méthode Dirac :
L'exemple suivant illustre les calculs quantiques en utilisant l'équation de Dirac.
On considère un fermion de Dirac libre (sans interaction externe), décrit par une fonction d'onde relativiste.
L'évolution temporelle de la fonction d'onde Ψ est alors donnée par l'équation de Dirac (relation D1) sous la forme :
(D1) (i h' γμ dμ - m c I4) Ψ(ct, x) = 0
qui s'explicite comme suit :
(D1*) i h' γ0 dΨ/d(ct) = (-i h' γk dk + m c I4)Ψ(ct, x)
avec :
k = 1, 2, 3 (composantes spatiales)
m = masse de la particule au repos.
I4 = matrice Identité 4x4
γμ = matrices 4x4 spécifiques introduites par Dirac.
x = vecteur spatial 3D = (x1, x2, x3)
dμ = dérivées partielles par rapport aux coordonnées xμ = (ct, x1, x2, x3) dans l'espace-temps de Minkowski.
Dans le cas ou l'on cherche les états propres Ψj du système (numérotés par l'indice j), la fonction d'onde Ψj(ct, x) peut se décomposer en une partie spatiale stationnaire et une partie temporelle oscillante, sous la forme :
(D2) Ψj(ct, x) = Ψj(x) T(ct)
La relation (D1*) devient alors :
(D3) i h' (1/T(ct)) dT(ct)/d(ct) γ0 Ψj(x) = (-i h' γk dk + m c I4) Ψj(x)
En multipliant à gauche les deux membres par la matrice γ0, et compte tenu de la propriété (γ0)2 = I4, la relation D3 devient :
(D4) i h' (1/T(ct)) dT(ct)/d(ct) I4 Ψj(x) = γ0 (-i h' γk dk + m c I4) Ψj(x)
Pour que cette relation soit vraie quel que soit t et x, il faut nécessairement que les deux membres soient des opérateurs matriciels agissant de manière identique sur Ψj(x), donc proportionnels à la matrice Identité (I4) avec un facteur scalaire commun Ej/c (l'énergie relativiste totale de la particule dans l'état propre Ψj).
Equation spatiale :
En conséquence, la relation (D4) devient :
(DS1) γ0 (-i h' γk dk + m c I4) Ψj(x) = (Ej/c) I4 Ψj(x)
On cherche alors une solution sous la forme d'une onde plane progressive :
(DS2) Ψj(x) = uj(pj) exp(i pj.x/h')
où :
pj = (p1, p2, p3) est le vecteur quantité de mouvement relativiste en référentiel inertiel, exprimée dans l'espace 3D = m γj vj où γj est le facteur de Lorentz (γj = (1 - vj2/c2)-1/2).
uj(pj) est un spineur associé à pj
pj.x est le produit scalaire spatial 3D = pjk xk
compte tenu de la dérivée spatiale dkexp(i pj.x/h') = (i pk/h') exp(i pj.x/h'), la relation (DS1) se simplifie comme suit :
(DS3) γ0 (γk pk + m c I4) uj(pj) = (Ej/c) I4 uj(pj)
On décompose ensuite le spineur uj(pj) en deux spineurs de Pauli Φj et Χj tel que :
(DS4) uj(pj) = (Φj, Χj)T
compte tenu de l'expression des matrices γ0 et γk, la relation DS3 devient alors un système couplé de deux équations :
(DS5) σk pk Χj = (Ej/c - m c) Φj
σk pk Φj = (Ej/c + m c) Χj
En substituant Χj dans la première équation, et compte tenu de l'expression des matrices de Pauli σ, on obtient :
(Ej/c - m c)(Ej/c + m c) Φj = (σk pk)2 Φj = pj2 I2 Φj
D'où l'expression de l'observable Ej :
(DS6) Ej = ±(pj2 c2 + m2 c4)1/2
Cette relation dite "de dispersion" correspond aux particules (électrons) pour l'énergie Ej positive et aux anti-particules (positrons) pour l'énergie Ej négative.
Il reste maintenant à exprimer Φj et Χj pour trouver uj(pj)
Pour l'électron (Ej > 0), la seconde équation DS5 donne :
(DS7) Χj = Φj σk pk/(Ej/c + m c)
Si * désigne le conjugué complexe sans transposition et si wj est un spineur de Pauli normalisé arbitraire (tel que (wj*)T.wj = 1), par exemple (1, 0)T pour un spin orienté selon l'axe +z, alors Φj peut être choisi comme suit :
Φj = ((Ej/c + m c)/(2 m c))1/2 wj afin de vérifier la relation de normalisation : (uj*(pj))T γ0 uj(pj) = 2 m c
Pour le positron (Ej < 0), la première équation DS5 donne :
(DS8) Φj = -Χj σk pk/(|Ej|/c + m c)
et Χj peut être choisi comme suit :
Χj = ((|Ej|/c + m c)/(2 m c))1/2 wj
Equation temporelle :
compte tenu de la constante (Ej/c) I4, la relation (D4) devient :
(DT0) i h' (1/T(ct)) dT(ct)/d(ct) I4 Ψj(x) = (Ej/c) I4 Ψj(x)
ou encore :
(DT1) dT(ct)/d(ct) + i Qj T(ct) = 0
avec :
(DT2) Qj = Ej/(c h')
qui admet pour solution :
(DT3) T(ct) = Cj exp(-i Qj ct) = Cj exp(-i Ej t/h')
avec Cj constante complexe arbitraire, qui vaut n'importe quel facteur de phase de module 1 (Cj = exp(i θj) avec θj nombre réel) afin de respecter la condition de normalisation de Ψj(ct, x).
Pour simplifier les calculs, on prend conventionnellement Cj = 1. Mais ce choix est arbitraire et doit être revu si des interférences ou des superpositions d'états sont étudiées, car les phases relatives entre différents états jouent un rôle crucial dans ces situations.
Fonction d'onde complète :
compte tenu des relations (D2)(DS2)(DS4)(DS7)(DS8)(DT3), la fonction d'onde normalisée complète pour tout état propre j est donc :
(DC1) Ψj(t, x) = (Φj, Χj)T exp(i θj) exp(i pj.x/h') exp(-i Ej t/h')
Cette solution élémentaire Ψj(t, x) décrit un fermion libre de spin 1/2 sous forme d'onde plane relativiste, dont l'énergie et la quantité de mouvement satisfont à la relation Ej2 = pj2 c2 + m2 c4.
Par superposition de ces états propres (paquets d'ondes), elle constitue le fondement de la description quantique relativiste, intégrant la prédiction de l'antimatière via les solutions à énergie négative.
Amplitudes de probabilité :
compte tenu de la relation DS2, la densité ρ de probabilité s'écrit alors :
(DD1) ρ = (Ψj*(x))T Ψj(x) = (uj*(pj))T uj(pj)
D7.10. Similitudes entre mécanique quantique et mécanique classique :
La mécanique classique, qui est déterministe et basée sur des trajectoires bien définies, contraste avec la mécanique quantique fondée sur des probabilités, des superpositions d'états et d'autres principe fondamentaux spécifiques à son domaine.
Toutefois, malgré ces différences conceptuelles fondamentales, les deux approches présentent un certain nombre de similitudes :
- Description du système isolé en termes d'objets (exemples : particules, solides) et d'interactions internes ou externes au système (exemples : forces, champs, interactions quantiques)
- Données (ou propriétés) intrinsèques (exemples : masse, dimensions, spin, niveaux d'énergie quantifiés d'un atome)
- Observables (exemples : position, vitesse, énergie, fonction d'onde, valeur propre)
- Conditions initiales (à t = 0) et conditions aux frontières du système (exemple : conditions aux bords pour une corde vibrante)
- Conservation de certaines quantités physiques (exemples : quantité de mouvement, moment cinétique, énergie)
- Constantes physiques universelles (exemples : accélération de la pesanteur (g), vitesse de la lumière (c), constante de Planck (h))
- Cadre de résolution (exemples : lois de la dynamique, équation de Schrödinger)
- Certains formalisme mathématiques (exemples : calcul différentiel et intégral, algèbre linéaire, équations différentielles)
- Calcul des observables (avec résultats déterministes ou probabilistes)
- Evolution du système dans le temps (exemples : trajectoires, fonction d'onde)
- Analyse et interprétation des résultats par comparaison entre prédictions théoriques et observations expérimentales, permettant de valider ou d'ajuster les modèles.
D7.11. Sources relatives à la physique quantique :
[ASP] Alain Aspect, Si Einstein avait su, Odile Jacob, 2025.
[BOU] Alain Bouquet, Noyaux et particules.
[COH] Cohen-Tannoudji, Mécanique quantique, Tome I, CNRS Editions
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
Réaliser un noeud exige des gestes précis, maîtrisés et adaptés à la situation.
Ni une simple vidéo, ni les conseils d'un auteur reconnu ne peuvent, à eux seuls, garantir une exécution correcte.
Pour apprendre et progresser en toute sécurité, il est donc préférable de s'appuyer sur des manuels officiels, des guides approuvés ou de suivre une formation encadrée.
La suite de cette page présente une compilation issue de plusieurs ouvrages spécialisés sur les noeuds, enrichie pour combler certaines lacunes et clarifier les imprécisions ou ambiguïtés que l'on peut parfois y rencontrer.
|
A retenir : Dans le cas de fortes charges ou variables (à-coups), les techniques largement validées en escalade, spéléo, nautisme et froissartage sont les suivantes : - Noeuds d'arrêt : pour bloquer une corde en extrémité, le noeud le plus sécuritaire est le Noeud en huit d'arrêt. - Noeuds de friction : pour faire coulisser une corde librement sans charge, tout en assurant un blocage automatique sous charge, l'autobloquant le plus couramment utilisé en escalade est le Noeud de Prusik. - Noeuds de jonction : pour lier deux cordes ensemble, le noeud priorisant simplicité, solidité et démontage est le Noeud de Zeppelin pour des diamètres identiques ou proches, et le Noeud de plein poing doublé pour des diamètres très différents. - Noeuds d'amarrage : pour fixer une corde à un point fixe (bitte, arbre, anneau, etc.), le noeud le plus sécuritaire est le Noeud en double huit sur bitte ou arbre, et le Noeud d'ancre sur anneau. - Noeuds de brêlage : pour lier deux pièces rigides ensemble (perches, rondins, etc.) à l'aide d'une corde, le noeud privilégié pour sa robustesse est le noeud de Surliure d'assemblage sur deux pièces parallèles et le noeud de Brêlage en diagonale sur deux pièces se croisant selon un angle quelconque. Existent également les Noeuds de décoration qui permettent de créer des motifs esthétiques. |
Sommaire :
D8.1. Liste des noeuds :
Le tableau ci-dessous liste les principaux noeuds utilisés dans la vie courante, classés par grandes catégories d'utilisation (cf. [PER][CHA]).
Légende du tableau : N/A = Non Applicable
| Catégorie | Noeud | Serrage | Utilisation | Fortes charges | Charges variables (à-coups) | Facilité de nouage | Facilité de dénouage (après forte charge) | Risque d'erreur (noeud instable) |
|---|---|---|---|---|---|---|---|---|
| Noeuds d'arrêt | Noeud en huit d'arrêt (ou noeud de Savoie) | bloquant | corde quelconque | oui | oui | simple | difficile | faible |
| Noeud simple | bloquant | corde quelconque | non | non | simple | difficile | serrage insuffisant | |
| Noeud de chirurgien | bloquant | fil de suture | oui | oui | complexe | très difficile | important | |
| Noeuds de friction (ou autobloquants) | Noeud de Prusik | semi-coulant | cordes différentes | oui | oui | simple | difficile | faible |
| Noeuds de jonction (ou d'ajut ou d'assemblage de cordes) | Noeud de Zeppelin (ou de Rosendahl) | bloquant | cordes identiques | oui | oui | simple | très facile | faible |
| Noeud de plein poing doublé | bloquant | cordes quelconques | oui | oui | simple | très difficile | serrage insuffisant | |
| Noeud de pêcheur | bloquant | cordes identiques | oui | oui | simple | difficile | important | |
| Noeud plat | bloquant | cordes identiques | non | non | simple | difficile | important | |
| Noeud d'écoute en jonction (ou noeud de tisserand marin) | bloquant | cordes différentes | non | non | simple | difficile | important | |
| Noeud de chirurgien en jonction | bloquant | cordes fines identiques | oui | oui | simple | difficile | important | |
| Noeuds d'amarrage (ou d'attache) | Noeud en double huit | bloquant | tout Support | oui | oui | simple | difficile | faible |
| Noeud d'ancre | bloquant | Support = anneau | oui | oui | complexe | difficile | important | |
| Noeud de chaise (ou noeud de bouline) | bloquant | tout Support | en traction seule | non | complexe | facile | important | |
| Noeud de papillon alpin (ou noeud de milieu d'alpinisme) | bloquant | tout Support en milieu de corde | oui | oui | complexe | facile | important | |
| Noeud de cabestan (ou noeud de batelier) | semi-coulant sur bitte, bloquant sur arbre ou anneau | tout Support | oui | non sur bitte, oui sur arbre ou anneau | simple | facile | important | |
| Noeud d'amarrage à tour mort et deux demi-clés | bloquant | tout Support | oui | oui | simple | difficile | faible | |
| Noeud constricteur | bloquant | tout Support | oui | oui | simple | très difficile | important | |
| Noeud de chirurgien en boucle | bloquant | tout Support | oui | oui | simple | difficile | serrage insuffisant | |
| Noeud d'hameçon à palette | bloquant | pêche légère | non | non | simple | difficile | faible | |
| Noeud coulant à plusieurs spires | coulant | tout Support | oui | oui | simple | difficile | faible | |
| Noeud de lasso (ou noeud Honda) | coulant | tout Support | oui | oui | complexe | difficile | important | |
| Noeud d'élingue à tonneau | coulant | Support cylindrique vertical | oui | non | complexe | difficile | faible | |
| Noeuds de brêlage (ou d'assemblage rigide) | Noeud de surliure d'assemblage | bloquant | deux rondins parallèles | non | non | complexe | difficile | important |
| Brêlage en diagonale (ou en croix) | bloquant | deux rondins formant un angle | oui | non | complexe | difficile | important | |
| Noeuds de décoration | Noeud de cravate Windsor | bloquant | cravate | N/A | N/A | complexe | facile | faible |
| Noeud carré chinois | bloquant | foulard | N/A | N/A | complexe | difficile | faible | |
| Noeud de capucin | semi-coulant | corde | oui | oui | simple | difficile | important |
D8.1.1. Noeud en huit d'arrêt :
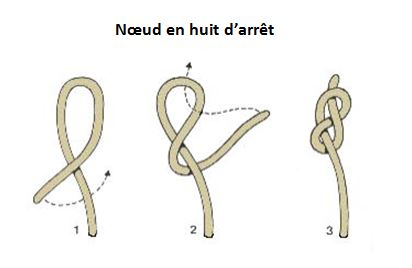
Le noeud en huit d'arrêt (ou noeud de Savoie) est un Noeud d'arrêt Bloquant, en extrémité de corde. Il peut supporter de fortes charges ou variables (à-coups).
Il est bien visible (volumineux) et difficile à dénouer.
Le noeud en huit d'arrêt est le standard le plus sûr pour des activités comme l'escalade, car il est simple à nouer, offre un risque d'erreur faible et présente une forme symétrique qui permet une vérification rapide.
A noter que ce noeud a une variante tout aussi sécurisée : le noeud en double huit. Ce dernier, plus volumineux, est rarement utilisé en escalade comme Noeud d'arrêt.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [MIS]) :
1. Passer le Brin courant par-dessus le Brin dormant pour former une petite boucle.
2. Faire le tour complet du Brin dormant.
3. Passer le Brin courant dans la boucle par-dessus (et non par-dessous).
4. Tirer sur les deux brins pour serrer et former la figure en "8".
D8.1.2. Noeud simple :
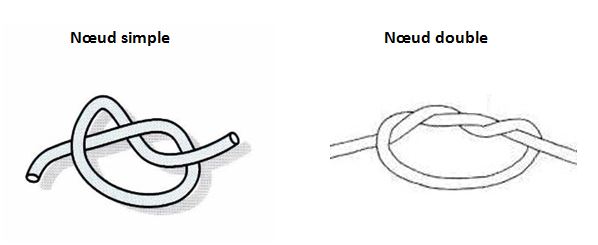
Le noeud simple (ou Demi-noeud) est un Noeud d'arrêt Bloquant, en extrémité de corde, pour faibles charges et constantes (sans à-coups).
Il est discret (peu volumineux), simple à nouer mais difficile à dénouer (voir Figure ci-dessus).
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
Le noeud simple doublé (ou noeud de capucin double) est une variante du noeud simple en passant deux fois le brin libre dans la boucle, équivalent à un Noeud de capucin à deux tours seulement (voir Figure ci-dessus).
Il est simple à nouer, plus résistant que le noeud simple et moins sensible au serrage imparfait, mais plus difficile à dénouer.
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
D8.1.3. Noeud de chirurgien :
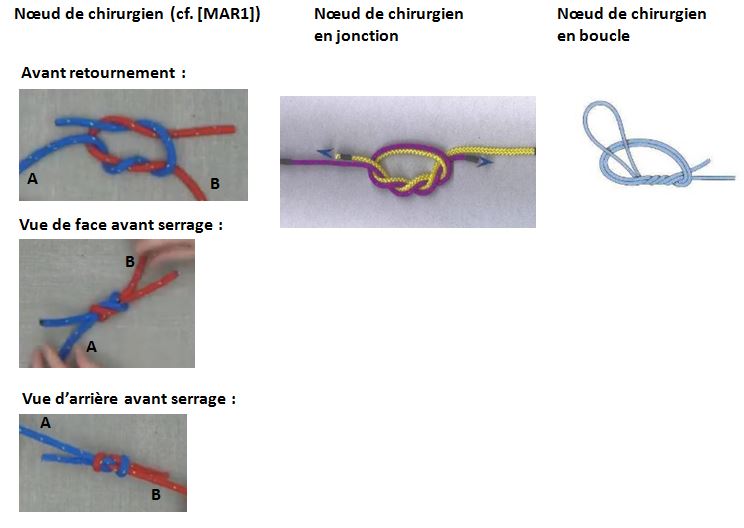
Le noeud de chirurgien est un Noeud d'arrêt Bloquant pour maintenir une tension entre deux points de suture. Il peut supporter de fortes charges ou variables (à-coups).
Il est complexe à nouer et quasiment impossible à dénouer.
Ce noeud est une variante du Noeud plat dans laquelle le premier tour simple du brin A autour de B est remplacé par plusieurs tours successifs, à la manière du Noeud de capucin (voir Figure ci-dessus, cf. [MAR1]). Cette modification ajoute de la friction et renforce la tenue du noeud.
Attention : ce noeud est instable s'il est mal exécuté aux étapes 3, 5 et 6.
Les étapes sont les suivantes, plus complexes que pour le Noeud plat (voir Figure ci-dessus, cf. [MAR1][MAR2]) :
1. Repérer un brin de référence (A) et le passer par-dessus l'autre brin (B), les deux brins formant une paire de cornes.
2. Faire deux tours complets du brin A autour de B et reformer la paire de cornes.
3. Passer à nouveau le brin A par-dessus le brin B et faire un second tour complet autour de B. Attention : si le croisement est réalisé derrière le brin B au lieu de devant, le noeud se défait entièrement lorsqu'on tire sur les deux brins longs ("noeud de vache").
4. Vérifier que le noeud présente deux boucles entrecroisées, avec les deux brins de chaque boucle passant tous deux par-dessous ou par-dessus le brin de la boucle opposée.
5. Tirer doucement sur les deux dormants pour "retourner" le noeud [MAR2]. Attention : vérifier le bon "retournement" comme suit : 1. Vue de face : deux brins obliques et parallèles traversent le centre du noeud, 2.
Vue arrière : deux boucles apparaissent aux extrémités du noeud.
6. Tirer fermement sur les deux paires de brins pour serrer le noeud.
D8.1.4. Noeud de Prusik :
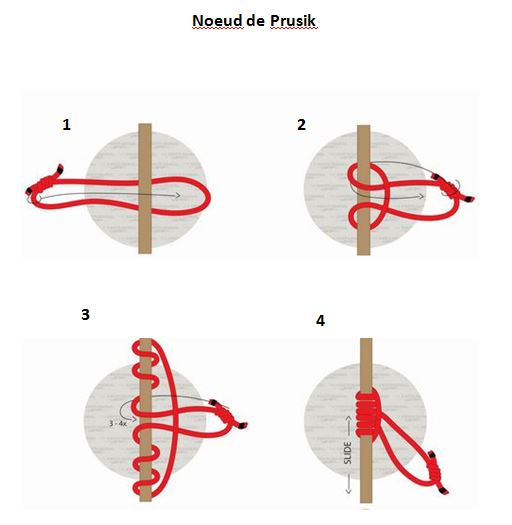
Le noeud de Prusik est un Noeud de friction Semi-coulant réalisé avec une boucle de cordelette enroulée autour d'une corde porteuse. Il coulisse librement lorsqu'il n'est pas chargé et se bloque automatiquement sous charge de façon symétrique (dans les deux sens de traction le long de la corde porteuse), ce qui en fait un système simple et fiable en escalade, secours ou travaux en hauteur.
Il peut supporter de fortes charges ou variables (à-coups) mais devient alors difficile à dénouer à cause des spires tassées.
Le noeud de Prusik est l'autobloquant le plus couramment utilisé en escalade, car il est simple à nouer, offre un risque d'erreur faible et présente une forme symétrique qui permet une vérification rapide.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [THE]) :
1. Utiliser une cordelette fermée en anneau (généralement par un Noeud de pêcheur double) et la positionner sur la corde porteuse de manière à former deux portions : une courte et une longue.
2. Tenir la portion courte et enrouler la portion longue autour de la corde porteuse en passant dans l'espace situé entre la corde porteuse et la portion courte.
3. Continuer l'enroulement en faisant plusieurs tours, toujours dans le même sens et en veillant à bien serrer chaque tour autour de la corde porteuse.
4.
Tirer doucemement sur la portion longue pour tasser les tours les uns contre les autres.
5. Pour plus de sécurité, attacher un mousqueton dans la portion longue formant la boucle mobile supportant la charge, afin de la connecter à votre matériel ou harnais.
D8.1.5. Noeud de Zeppelin :
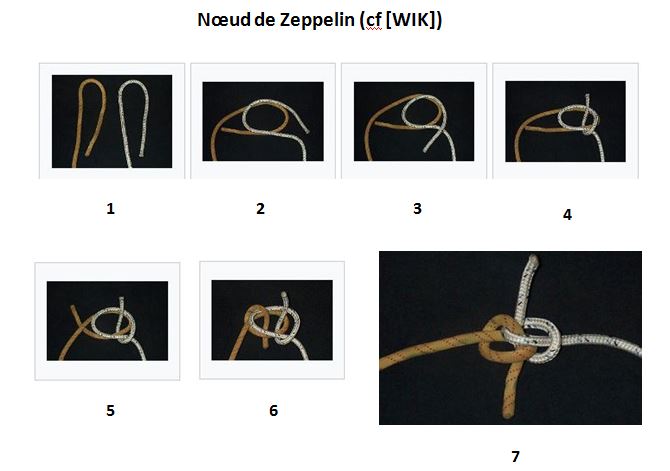
Le noeud de Zeppelin (ou de Rosendahl) est un Noeud de jonction Bloquant. Il permet d'assembler deux cordes de même diamètre sous fortes charges ou variables (à-coups).
Il est simple à nouer, offre un risque d'erreur faible et présente une forme symétrique qui permet une vérification rapide.
Il a deux avantages distinctifs que n'ont pas les autres Noeuds de jonction :
- Il peut être mis en charge avant d'être complètement serré, ce qui permet de l'utiliser dans des situations où la charge varie avant le serrage définitif.
- Il est très facile à dénouer, même après avoir supporté des charges importantes.
Le noeud de Zeppelin, comme le Noeud de pêcheur double, est le Noeud de jonction le plus sécuritaire sur des cordes de même diamètre (mais pas sur cordes de diamètres différents).
Il est souvent préféré au Noeud de pêcheur double pour les deux avantages pré-cités.
Il existe plusieurs méthodes pour réaliser ce noeud. Les étapes de la méthode dite "symétrique" sont les suivantes (voir Figure ci-dessus, cf. [WIK, Noeud de Zeppelin]) :
1. Former deux Ganses identiques, orientées dans le même sens.
2. Superposer les deux Ganses en position tête-bêche (à 180°).
3. Prendre le Brin courant de la Ganse du dessus et le croiser au-dessus de son Brin dormant.
4. Avec ce Brin courant, entourer les deux brins en passant par dessous et ressortir de la boucle vers le dessus.
5. Prendre le Brin courant de l'autre Ganse et le croiser au-dessous de son Brin dormant.
6. Avec ce le Brin courant, entourer les deux brins en passant par dessus et ressortir de la boucle vers le dessous.
7. Serrer progressivement et de manière équilibrée en tirant alternativement sur les Brins courants puis sur les Brins dormants.
8. Vérifier que le noeud présente deux barres parallèles encadrées par deux petites oreilles, avec Brins courants perpendiculaires aux Brins dormants, le motif étant identique en face arrière.
D8.1.6. Noeud de plein poing doublé :

Le noeud de plein poing doublé est un Noeud de jonction Bloquant utilisé en escalade. Il permet d'assembler deux cordes de diamètres identiques ou différents, sous fortes charges ou variables (à-coups).
Il est simple à nouer et très difficile à dénouer.
Grâce à son coeur décalé par rapport à l'axe de tension des cordes, les deux noeuds simples se compriment mutuellement en butée sans risque de retournement ou d'échappement.
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
Le noeud de plein poing doublé est le Noeud de jonction le plus sécuritaire sur des cordes de diamètres différents (et moins sur cordes de même diamètre).
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [MAG1][MAG2][ARN2]) :
1. Aligner les deux cordes parallèlement et dans le même sens.
2. Avec la paire de Brins courants, réaliser un premier Noeud simple englobant les deux cordes.
3. Serrer le noeud brin par brin en tirant successivement et séparément sur chacun des quatre brins. Contrôler la symétrie du coeur.
4. Avec la paire de Brins dormants, réaliser un second Noeud simple identique au premier et dans le même sens. Amener ce second noeud en butée contre le premier puis le serrer en tirant simultanément sur les deux brins sortants du noeud, du côté des brins dormants.
5. Tirer simultanément et en opposition sur les deux Brins dormants de chaque corde afin de comprimer les deux noeuds l'un contre l'autre.
D8.1.7. Noeud de pêcheur :
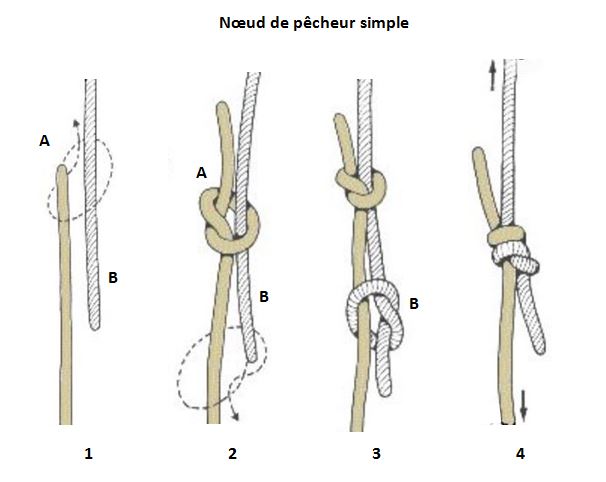
Le noeud de pêcheur simple (ou joint anglais) est un Noeud de jonction Bloquant. Il permet d'assembler deux cordes de même diamètre sous fortes charges ou variables (à-coups). Il convient en particulier pour des cordes fines.
Le noeud de pêcheur simple est en fait l'assemblage de deux Noeuds simples serrés l'un contre l'autre, en opposition parfaite.
Il est simple à nouer et difficile à dénouer.
Attention : ce noeud est instable s'il est mal exécuté aux étapes 3 et 4.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [PIN][MAR3]) :
1. Présenter les deux brins A et B en position tête-bêche sur le plan de travail, avec les extrémités se chevauchant.
2. Avec le brin A, faire un Noeud simple autour du brin B, sans trop serrer pour que les deux noeuds puissent glisser l'un vers l'autre lors du serrage final.
3. Retourner le montage de 180° dans le plan de travail (ce qui revient à inverser le haut et le bas) et répéter les mêmes gestes avec le brin B. La rotation de 180° garantit une symétrie correcte, les deux noeuds pouvant s'emboîter et non se contrarier à la fin du montage.
4. Tirer progressivement sur les deux brins longs pour rapprocher les deux noeuds, les emboîter et les serrer fermement l'un contre l'autre.
5. Vérifier que le noeud présente deux barres parallèles sur le dessus et deux X croisés sur le dessous.

Le noeud de pêcheur double est une variante du noeud de pêcheur simple, encore plus sécuritaire mais plus difficile à dénouer.
Le noeud de pêcheur double est en fait l'assemblage de deux Noeuds coulants à deux spires serrés l'un contre l'autre, en opposition parfaite. Le brin A s'enroule autour du brin B comme un noeud coulant à deux tours s'enroulerait autour de son dormant.
Comme le Noeud de Zeppelin, le noeud de pêcheur double est le Noeud de jonction le plus sécuritaire sur des cordes de même diamètre (mais pas sur cordes de diamètres différents).
Attention :
- En fin de montage, les deux noeuds ont la même forme générale que celle de deux Noeuds doubles mis côte à côte, mais avec une différence essentielle : le brin B ne passe pas dans la boucle laissée par A (voir étape 2 de la Figure "Noeud de pêcheur simple"), mais il remonte à l'intérieur des deux tours (voir étape 4 de la Figure "Noeud de pêcheur double"), serrant ainsi plus efficacement la double torsade.
- Ce noeud est instable s'il est mal exécuté aux étapes 6 et 7.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [COR][MIN]) :
1. Présenter les deux brins A et B en position tête-bêche sur le plan de travail, avec les extrémités se chevauchant.
2. Avec le brin A, faire un premier tour autour du brin B en longeant le brin B vers son extrémité et en chevauchant les deux brins.
3. Passer en dessous de B pour commencer le deuxième tour, toujours en revenant vers l'extrémité de B. Les deux spires doivent être assez larges pour permettre un passage de doigt.
4. Terminer le deuxième tour, puis passer l'extrémité A dans les deux tours.
5. Tirer sur les brins du même noeud, sans trop serrer pour que les deux noeuds puissent glisser l'un vers l'autre lors du serrage final.
6. Retourner le montage de 180° dans le plan de travail (ce qui revient à inverser le haut et le bas) et répéter les mêmes gestes avec le brin B. La rotation de 180° garantit une symétrie correcte, les deux noeuds pouvant s'emboîter et non se contrarier à la fin du montage.
7. Tirer progressivement sur les deux brins longs pour rapprocher les deux noeuds, les emboîter et les serrer fortement l'un contre l'autre.
8. Vérifier que le noeud présente quatre barres parallèles sur le dessus et deux X croisés sur le dessous.
D8.1.8. Noeud plat :
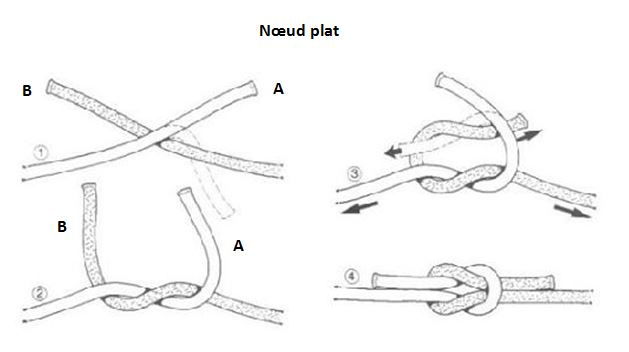
Le noeud plat est un Noeud de jonction Bloquant. Il permet d'assembler deux cordes de même diamètre sous faibles charges et constantes (sans à-coups).
Il est simple à nouer et difficile à dénouer.
Attention : ce noeud est instable ("noeud de vache") s'il est mal exécuté à l'étape 3.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [GRU]) :
1. Repérer un brin de référence (A) et le passer par-dessus l'autre brin (B), les deux brins formant une paire de cornes.
2. Faire un tour complet du brin A autour de B et reformer la paire de cornes.
3. Passer à nouveau le brin A par-dessus le brin B et faire un second tour complet autour de B. Attention : si le croisement est réalisé derrière le brin B au lieu de devant, le noeud se défait entièrement lorsqu'on tire sur les deux brins longs ("noeud de vache").
4. Vérifier que le noeud avant serrage présente deux boucles entrecroisées, avec les deux brins de chaque boucle passant tous deux par-dessous ou par-dessus le brin de la boucle opposée.
5. Tirer sur les deux paires de brins pour serrer le noeud.
D8.1.9. Noeud d'écoute en jonction :
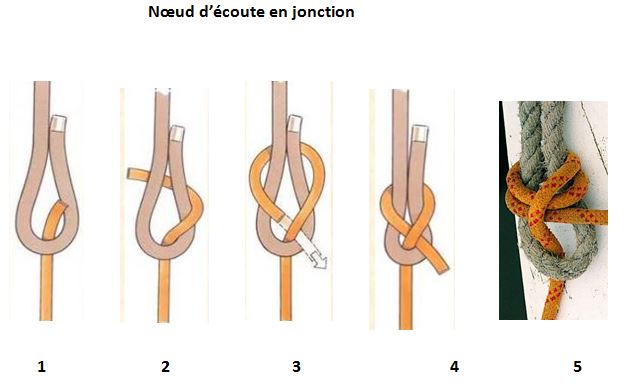
Le noeud d'écoute en jonction (ou noeud de tisserand marin) est un Noeud de jonction Bloquant. Il permet d'assembler deux cordes de diamètres différents sous faibles charges et constantes (sans à-coups).
Il est simple à nouer et difficile à dénouer.
Attention : ce noeud est instable s'il est mal exécuté aux étapes 1 et 2.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [SCE][DIM]) :
1. Faire une boucle large et non fermée avec le brin épais. Attention : une boucle trop petite peut induire un pincement au serrage insuffisamment progressif avec frottement réduit et inégal.
2. Passer le brin fin sous la boucle et faire le tour complet des deux brins épais de la boucle dans le même sens que la formation initiale de la boucle. Attention : inverser le sens donne un noeud instable.
3. Contrairement au Noeud plat, ne pas repasser le brin fin dans la boucle mais le passer le long du côté entre le brin épais et le brin fin. Attention : vérifier que les deux brins courts se retrouvent du même côté latéral du noeud.
4. Tirer sur les brins les plus longs (épais et fin) afin de bloquer le noeud.
5. Variante pour sécuriser le noeud lorsque la charge est importante (noeud d'écoute double) : rajouter un second tour en passant sous le brin fin.
D8.1.10. Noeud de chirurgien en jonction :
Le noeud de chirurgien en jonction est un Noeud de jonction Bloquant utilisé en pêche. Il permet d'assembler deux cordes fines de même diamètre, sous fortes charges ou variables (à-coups).
Il est simple à nouer et difficile à dénouer.
Ce noeud est une variante du Noeud de capucin, réalisée en doublant la corde (voir schéma dans Noeud de chirurgien).
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
D8.1.11. Noeud en double huit :
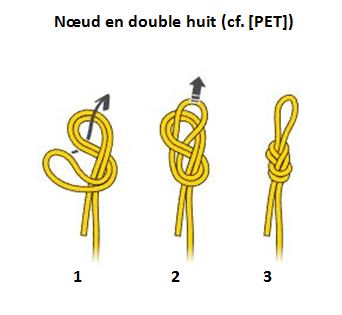
Le noeud en double huit est un noeud Bloquant utilisé comme Noeud d'arrêt ou Noeud d'amarrage, notamment pour s'encorder en montagne. Il peut supporter de fortes charges ou variables (à-coups).
Il ne nécessite pas de Noeud d'arrêt supplémentaire, est simple à nouer et peu sujet aux erreurs.
En revanche, il est difficile à dénouer, notamment après tensions prolongées ou chutes répétées, ce qui limite son utilisation aux amarrages durables plutôt que temporaires.
Ce noeud est une variante du Noeud en huit, réalisée en doublant la corde (voir Figure ci-dessus, cf. [PET][ALP]).
Ce noeud est le Noeud d'amarrage le plus sécuritaire sur Support de type bitte ou arbre (mais pas sur anneau).
En pratique cependant, le noeud en double huit ne se noue pas autour d'un Support, ce qui obligerait à tirer toute la longueur de corde pour la passer dans la boucle. En fait, quel que soit le Support (bitte, arbre ou anneau) :
A. On forme d'abord la boucle en extrémité de corde.
B. On fait un ou plusieurs Tours morts du Support avec le Brin courant.
C. On referme le système par un connecteur (mousqueton, maillon rapide, etc.) reliant la boucle au Brin dormant tendu, sans re-nouer. L'ancrage est dit "sans tension" (si un ou plusieurs Tours morts) ou "tendu" (si seulement un quasi-tour de l'arbre).
D8.1.12. Noeud d'ancre :

Le noeud d'ancre est un Noeud d'amarrage bloquant, utilisable essentiellement sur un anneau ou une manille. Il peut supporter de fortes charges ou variables (à-coups).
Il est complexe à nouer et difficile à dénouer.
Sa réalisation est similaire à celle d'un Noeud d'amarrage à Tour mort et deux Demi-clé, mais les Demi-clés ne sont pas identiques, la première (a) se faisant sur les deux boucles entourant l'anneau, la seconde (b) sur le Brin dormant (voir Figure ci-dessus, cf. [PON]).
Ce noeud est le Noeud d'amarrage le plus sécuritaire sur anneau (mais pas sur bitte ou arbre) car il offre une friction optimale dans un espace restreint grâce à l'enroulement serré de la corde autour de la section relativement petite de l'anneau.
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
D8.1.13. Noeud de chaise :
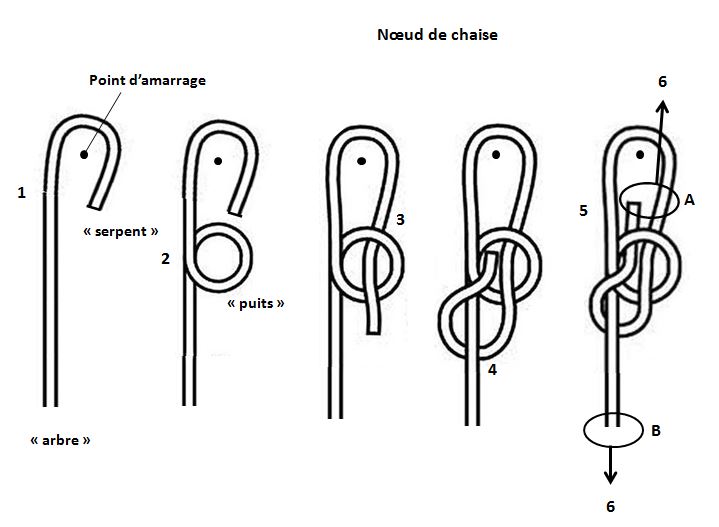
Le noeud de chaise (ou noeud de bouline) est un Noeud d'amarrage Bloquant qui ne glisse pas et permet de tenir de fortes charges en traction seule (sans torsion, ni vibrations, ni chocs répétés).
Il est complexe à nouer et facile à dénouer, même après une forte tension, ce qui le rend idéal pour les amarrages temporaires.
Attention : le noeud de chaise est instable (faux noeud de chaise) s'il est mal exécuté à l'une des étapes 3, 4, 5 ou 6.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [COM][ARN1]) :
Moyen mnémotechnique : le serpent sort du puits, fait le tour de l'arbre et rentre dans le puits.
1. Faire une grande boucle autour du point d'amarrage (arbre, anneau...). La corde présente alors deux brins :
- le Brin dormant (appelé "arbre") qui supportera la charge,
- le Brin courant (appelé "serpent") qui servira à former le noeud.
2. On forme avec l'arbre une boucle (appelée "puits") orientée côté serpent (et non côté opposé).
3. On place le serpent au fond du puits, c'est-à-dire au centre de la boucle et du même côté que l'arbre par rapport au plan de la boucle. Attention : si le serpent est placé de l'autre côté, on obtient un faux noeud de chaise.
4. Le serpent sort du puits et fait le tour de l'arbre en passant par l'arrière. Attention : si le serpent croise l'arbre avant de passer derrière, on obtient un faux noeud de chaise.
5. Le serpent rentre dans le puits en parallèle des deux brins de la boucle d'amarrage, sans croisement. Attention : si le serpent croise les deux brins de la boucle au lieu de rester parallèle, on obtient un faux noeud de chaise.
6. On serre ensuite le noeud en tenant d'un côté le serpent et la partie adjacente de la boucle d'amarrage (partie A), et de l'autre l'arbre (partie B), tout en veillant à ce qu'ils partent dans des directions opposées par rapport au puits. Attention : dans le cas contraire, le puits peut se renverser comme une chaussette et le noeud se défait complètement.
7. Pour prévenir tout desserrage accidentel, rajouter un Noeud d'arrêt (Noeud en huit par exemple) sur le Brin courant, collé contre le noeud de chaise.
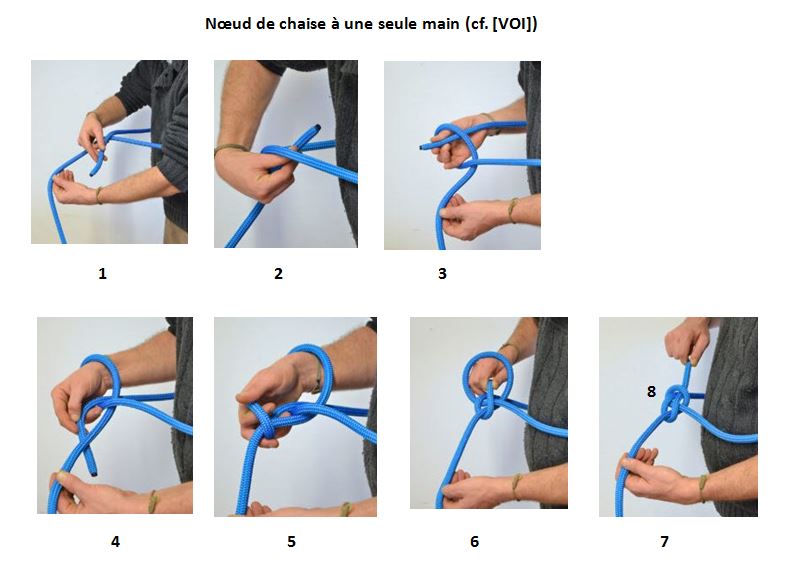
A noter que ce noeud pour se faire sur soi d'une seule main selon une technique rapide pratiquée en escalade.
Attention : le noeud de chaise à une main peut être instable et dangereux (faux noeud de chaise) s'il est mal exécuté, notamment à l'étape 6.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [VOI][KIN][ARN1]) :
1. Faites le tour de votre taille avec la corde puis positionnez le Brin courant par-dessus le Brin dormant.
2. En tournant le poignet, faites une Demi-clé.
3. Retournez le poignet, paume vers le haut.
4. Repassez ensuite le Brin courant sous le Brin dormant, toujours avec la même main.
5. Saisissez l'extrémité et faites-la passer sur le Brin dormant.
6. Tout en tenant le Brin dormant de la main gauche, tirez le Brin courant de la corde en le faisant passer à l'intérieur de la boucle dans laquelle était le poignet, et renverser le noeud en tirant sur le Brin dormant. Attention : il faut tirer modérément, juste ce qu'il faut pour libérer la boucle. Dans le cas contraire, le noeud est instable ou reste ouvert.
7. Serrer le noeud en tirant simultanément sur les deux brins (Courant et Dormant).
8. Pour prévenir tout desserrage accidentel, rajouter un Noeud d'arrêt (Noeud en huit par exemple) sur le Brin courant, collé contre le noeud de chaise.
D8.1.14. Noeud de papillon alpin :

Le noeud de papillon alpin (ou noeud de milieu d'alpinisme) est un Noeud d'amarrage Bloquant, réalisé en milieu de corde pour des ancrages intermédiaires, l'encordement en milieu de cordée ou l'isolation d'une section de corde endommagée. Il peut supporter de fortes charges ou variables (à-coups)
Il est complexe à nouer et facile à dénouer, même après fortes tensions.
Attention : ce noeud est instable s'il est mal exécuté à l'une des étapes.
Il existe plusieurs méthodes pour réaliser ce noeud, donc celle dite "de la main" qui minimise le risque de faux-noeud. Les étapes sont les suivantes (voir Figure ci-dessus, cf. [WIK, Noeud de papillon alpin][SAU][NOD]) :
1. Poser la corde verticalement sur la paume ouverte de la main et former trois tours parallèles, sans chevauchement des brins, en progressant vers les doigts.
2. Avec l'autre main, saisir le brin du milieu par-dessous et le tirer en direction des doigts en formant une Ganse.
3. Ramener la Ganse par-dessus les deux autres brins restés dans la main, l'enrouler autour d'eux et la faire ressortir à nouveau en direction des doigts.
4. Retirer la main des tours et serrer fermement le noeud en tirant symétriquement sur la Ganse et sur les deux brins sortants de la corde.
5. Avant mise en charge, vérifier que le noeud présente deux petites pattes en face avant et un X bien formé en face arrière, qui se transforment après charge en un X aplati en face avant et deux barres parallèles en face arrière.
Une variante de ce noeud existe (cf. [AND]), en posant la corde derrière la paume ouverte de la main (et non devant). Le noeud obtenu est identique mais avec une inversion des brins gauche/droite.
D8.1.15. Noeud de cabestan :

Le noeud de cabestan (ou noeud de batelier) est un Noeud d'amarrage Semi-coulant sur bitte et bloquant sur arbre ou sur anneau. Il permet de fixer une corde sous tension à un point fixe, comme une bitte d'amarrage.
Il peut supporter de fortes charges constantes (sans à-coups) sur bitte et variables (à-coups) sur arbre ou anneau.
Il est simple à nouer et facile à dénouer.
Attention : ce noeud est instable s'il est mal exécuté aux étapes 2 et 3.
Sur une bitte, les étapes sont les suivantes (voir Figure ci-dessus, cf. [ENA][ANI][NAU]) :
1. Faire un Tour mort autour de la bitte pour absorber la tension de la corde et la stabiliser [ENA]. Cette étape est fortement conseillée avant de réaliser le noeud de cabestan proprement dit (étapes suivantes).
2. Former une première boucle horizontale (Demi-clé) en passant le Brin courant sous le Brin dormant [ANI][NAU] et l'empiler sur la bitte.
3. Former une seconde boucle horizontale de façon identique à la première [ANI][NAU] et l'empiler sur la bitte, ce qui crée la forme croisée emblématique du noeud de cabestan. A noter que cette seconde boucle apparait alors inversée par rapport à la première. C'est en effet la méthode de formation (brin libre sous brin fixe), répétée deux fois, qui inverse visuellement le sens des deux boucles.
4. Former une troisième boucle et l'empiler sur la bitte pour sécuriser l'ensemble en cas de distension du Brin dormant.

A noter que ce noeud peut se faire autour d'un point fixe ne présentant pas d'extrémité libre, comme un arbre ou un anneau.
Attention : ce noeud est instable s'il est mal exécuté aux étapes 2 et 3.
Les étapes sont alors les suivantes (voir Figure ci-dessus, cf. [LYO][QUE, repère 18:30]) :
1. Le Tour mort autour de l'arbre est inutile dans cette situation car le premier tour serré de l'étape suivante (étape 1) suffit à absorber la tension de la corde et à la stabiliser.
2. Faire un premier tour complet autour de l'arbre (Demi-clé) en passant le Brin courant sous le Brin dormant. Astuce : pour que cette boucle reste bien serrée pendant la réalisation de la seconde, il est préférable de coincer provisoirement le Brin courant entre l'arbre et le Brin dormant, plutôt que de simplement le placer géométriquement "sous" le Brin dormant [QUE, repère 18:30].
3. Croiser le Brin courant au-dessus du Brin dormant puis effectuer un second tour identique au premier.
4. Tirer sur le Brin courant pour serrer le noeud.
D8.1.16. Noeud d'amarrage à Tour mort et deux Demi-clés :
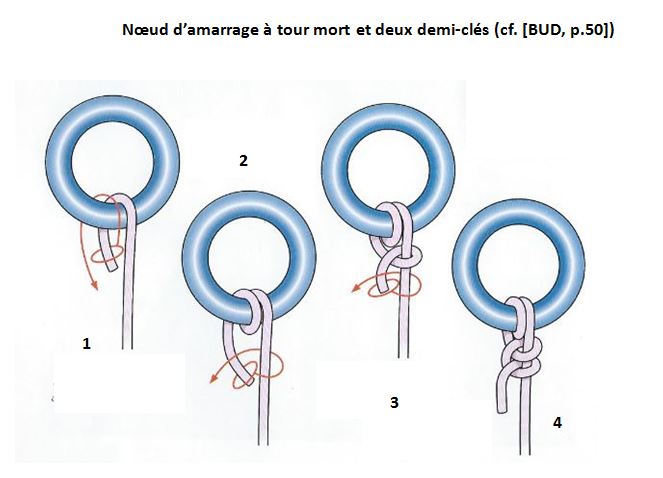

Le noeud d'amarrage à Tour mort et deux Demi-clés est un Noeud d'amarrage bloquant, utilisable sur tout Support externe (bitte, arbre, anneau, etc.). Il peut supporter de fortes charges ou variables (à-coups).
Ce noeud est simple à nouer, peu sujet aux erreurs et difficile à dénouer.
Sa réalisation est similaire à celle d'un Noeud de cabestan sur arbre, avec un Tour mort préalable, mais les deux Demi-clés se font sur le Brin dormant et non sur la bitte (voir Figure de gauche ci-dessus, cf. [BUD, p.50]).
Cette différence fait que les Demi-clés travaillent en enroulement et serrage sur le Brin dormant, et non en étranglement autour de la bitte, ce qui donne un meilleur blocage sous charge et aussi une plus grande aptitude aux charges variables (à-coups).
Pour un amarrage sur bitte, le noeud d'amarrage à Tour mort et deux Demi-clés est plus sécuritaire que le Noeud de cabestan car il est totalement Bloquant et non Semi-coulant.
Ce noeud présente plusieurs variantes, dont :
- Variante avec une seule Demi-clé ("demi-cabestan nautique").
- Variante avec première Demi-clé remplacée par une Clé (voir Figure de droite ci-dessus, cf. [SAI]).
D8.1.17. Noeud constricteur :

Le noeud constricteur est un Noeud d'amarrage bloquant. Il peut supporter de fortes charges ou variables (à-coups).
C'est une variante du Noeud de cabestan sur arbre, beaucoup plus serrant.
Il est simple à nouer et quasi-impossible à dénouer.
Attention : ce noeud est instable s'il est mal exécuté aux étapes 1 et 2.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [WIK, Noeud constricteur]) :
1. Faire un tour complet autour de l'arbre en passant le Brin courant en dessous du Brin dormant.
2. Faire un second tour en passant le Brin courant au-dessus du Brin dormant...
3. ...puis par dessous le premier tour.
4. Tirer sur le Brin courant pour serrer.
D8.1.18. Noeud de chirurgien en boucle :
Le Noeud de chirurgien en boucle est un Noeud d'amarrage Bloquant pour tirer une charge. Il peut supporter de fortes charges ou variables (à-coups).
Il est simple à nouer et difficile à dénouer.
Ce noeud est une variante du Noeud de capucin, réalisée en doublant la corde (voir schéma dans Noeud de chirurgien).
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
D8.1.19. Noeud d'hameçon à palette :
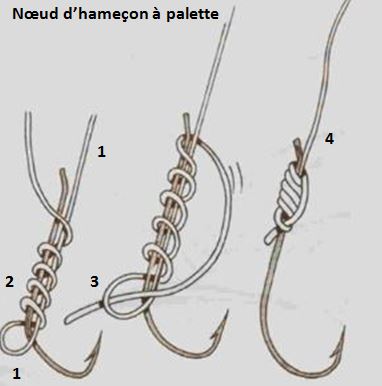
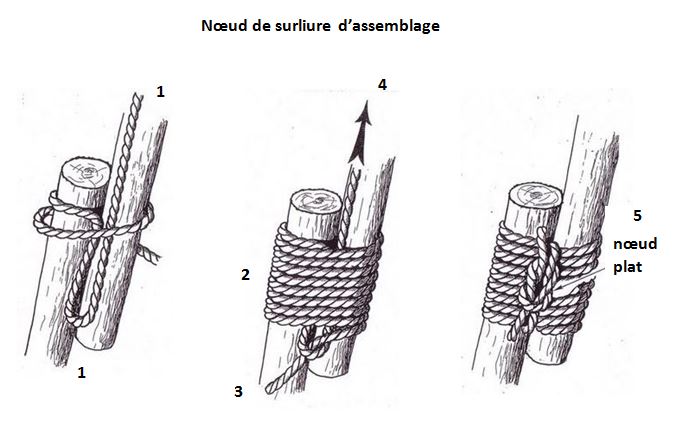
Le noeud d'hameçon à palette est un Noeud d'amarrage Bloquant, utilisé en pêche légère, qui permet d'attacher un fil de pêche le long d'un hameçon à palette (sans oeillet), en assurant un bon alignement du fil avec la palette.
Il supporte de faibles charges et constantes (sans à-coups).
Il est simple à nouer, peu sujet aux erreurs et difficile à dénouer.
Sa réalisation est identique à celle du Noeud de surliure d'assemblage sur deux rondins parallèles faisant office de hampe d'hameçon.
Les étapes sont les suivantes (voir Figures ci-dessus, cf. [PEC]) :
1. Disposer le fil (ou la corde) le long de la hampe de l'hameçon en faisant une boucle côté opposé à la palette et terminée par un brin libre suffisamment long.
2. Maintenir fermement la boucle entre le pouce et l'index, puis enrouler le brin libre autour de la hampe de l'hameçon, depuis la boucle vers la palette, en faisant une dizaine de tours jointifs et bien serrés. Dans le cas de la surliure d'assemblage, les habitudes de matelotage présentent souvent l'enroulement inverse (en progressant vers la boucle) qui reste correct mais avec une résistance mécanique à la traction moindre [SCO].
3. Maintenir le dernier tour entre le pouce et l'index, puis passer le brin libre dans la boucle.
4. Tirer simultanément et fermement sur les deux brins pour serrer le noeud.
5. Dans le cas de la surliure d'assemblage, pour une meilleure solidité, attacher ensemble les deux brins au moyen d'un Noeud plat [SCO].
D8.1.20. Noeud coulant à plusieurs spires :
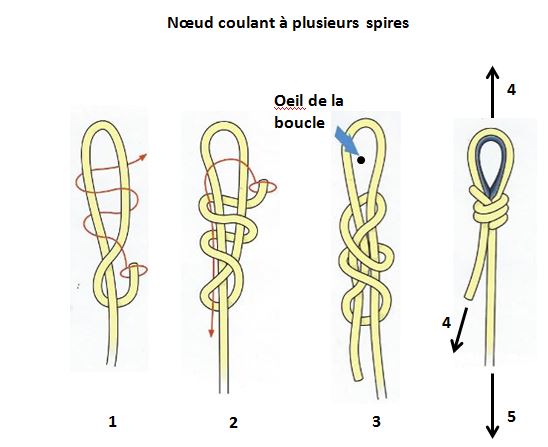
Le noeud coulant à plusieurs spires est un Noeud d'amarrage Coulant qui se resserre automatiquement autour d'un objet lorsqu'il est tiré. Il peut supporter de fortes charges ou variables (à-coups).
Il est simple à nouer, peu sujet aux erreurs et difficile à dénouer.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [BUD, p.62][KIM]) :
1. Faire une boucle avec le Brin courant puis le ramener à la base de la boucle en faisant un tour autour du Brin dormant.
2. Avec le Brin courant, enrouler les deux brins de la base de la boucle par plusieurs spires jointives remontant vers l'oeil de la boucle. Les spires doivent être assez larges pour permettre un passage de doigt.
3. Depuis l'oeil, faire passer l'extrémité du Brin courant sous l'ensemble des spires pour la faire ressortir du côté du Brin dormant.
4. Tirer sur la boucle et sur le Brin courant pour serrer et compacter les spires, en les maintenant bien jointives.
5. Tirer sur le Brin dormant ou appliquer une charge, afin de faire resserrer la boucle autour de l'objet.
D8.1.21. Noeud de lasso :
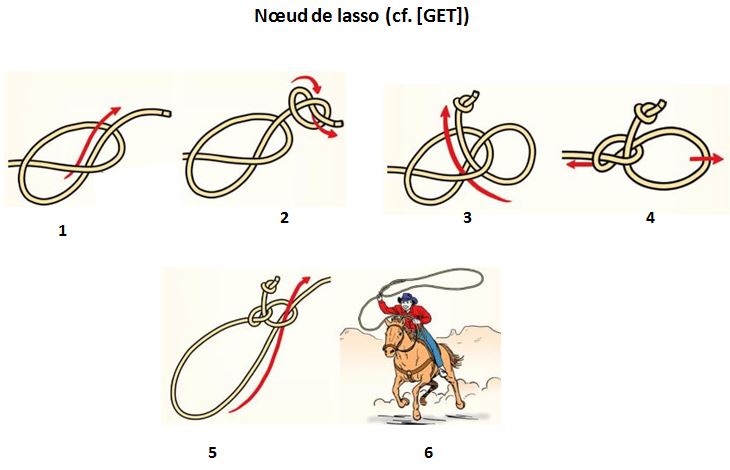
Le noeud de lasso (ou noeud Honda) est un Noeud d'amarrage Coulant qui se resserre automatiquement autour d'un objet lorsqu'il est tiré. Il peut supporter de fortes charges ou variables (à-coups).
Il est complexe à nouer et difficile à dénouer.
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [GET][WHY]) :
1. A 60 cm de l'extrémité de la corde, faire un Noeud simple non serré, en laissant la boucle lâche.
2. A l'extrémité de la corde, faire un Noeud simple serré, qui servira de Noeud d'arrêt.
3. Passer ce noeud d'arrêt dans la boucle lâche en l'introduisant par la petite ouverture ovale située entre le brin sortant et le brin entrant de cette boucle, puis le faire ressortir de l'autre côté. Cela crée automatiquement une petite boucle externe qui sera la boucle coulissante du lasso.
4. Serrer fermement la boucle lâche au contact du noeud d'arrêt afin de verrouiller le montage.
5. Passer la corde principale dans la petite boucle, en laissant une grande boucle externe qui sera la boucle du lasso.
6. Tenir la boucle du lasso dans la main dominante, la faire tournoyer au-dessus de la tête avec un mouvement fluide et régulier (swing), viser la cible puis lancer la boucle pour qu'elle s'enroule autour de cette cible. Tirer ensuite sur la corde principale pour resserrer la boucle et bloquer la cible.
D8.1.22. Noeud d'élingue à tonneau :

Le noeud d'élingue à tonneau est un Noeud d'amarrage Coulant utilisé pour lever en toute sécurité une charge cylindrique en position verticale (comme un tonneau par exemple). Il peut supporter de fortes charges et constantes (sans à-coups).
Il est complexe à nouer, peu sujet aux erreurs et difficile à dénouer.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [KNO]) :
1. Poser au sol une grande boucle formée en Noeud en huit.
2. Poser le tonneau sur le brin principal, au centre de la boucle.
3. Relever les deux brins libres à la verticale, de chaque côté du tonneau.
4. Lier les brins ensemble par un Noeud de jonction sécurisé (généralement un Noeud de pêcheur double) situé sur le côté du tonneau pour éviter qu'il soit écrasé par la charge suspendue.
5. Tester la tension avant le levage complet.
D8.1.23. Noeud de surliure d'assemblage :
Le noeud de surliure d'assemblage est un Noeud de brêlage Bloquant qui permet de relier ensemble deux perches parallèles ou de consolider une fracture sur un manche d'outil.
Il supporte de faibles charges et constantes (sans à-coups).
Il est complexe à nouer et difficile à dénouer.
Attention : ce noeud est instable s'il n'est pas suffisamment serré.
Sa réalisation est identique à celle du Noeud d'hameçon à palette (voir étapes et Figure associée).
D8.1.24. Brêlage en diagonale :
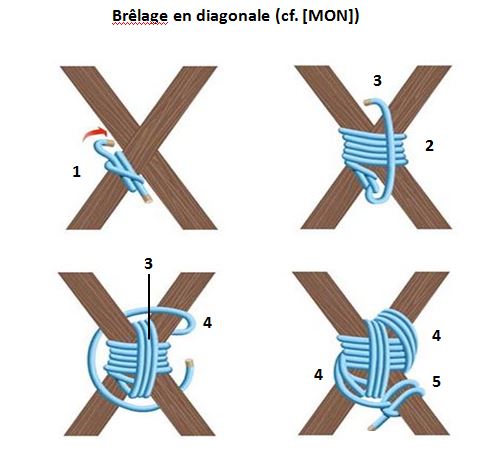
Le brêlage en diagonale (ou en croix) est une technique d'assemblage Bloquant qui permet de solidariser deux rondins se croisant selon un angle quelconque (aigu, droit ou obtus). Il peut supporter de fortes tensions constantes (sans à-coups).
Il est complexe à nouer et difficile à dénouer.
Attention : ce noeud est instable si les tours se chevauchent ou s'il n'est pas suffisamment serré.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [MON][REG][QUE]) :
0. Prévoir un méplat sur les rondins au niveau de l'assemblage pour éviter qu'ils ne roulent.
1. Faire un Noeud de cabestan sur l'un des rondins (point de départ).
2. Enrouler les deux rondins en diagonale avec trois tours de corde serrés, en veillant à ce que les brins soient parallèles et sans chevauchement.
3. Répéter l'opération sur l'autre diagonale. Ces deux séries de tours forment la croix caractéristique du brêlage en croix.
4. Enrouler la partie contact des deux rondins avec trois tours de corde perpendiculaires aux tours diagonaux.
5. Finir par un Noeud de cabestan sur l'un des deux rondins pour bloquer le brêlage.
6. Ajouter un Noeud d'arrêt (souvent un Noeud en huit) sur le brin libre du cabestan final pour éviter tout desserrage accidentel.
D8.1.25. Noeud de cravate Windsor :
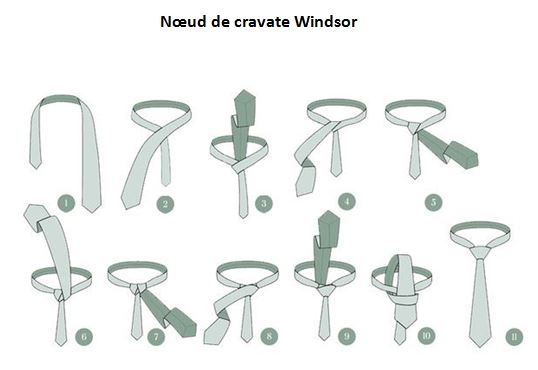
Le noeud de cravate Windsor est un Noeud de décoration Bloquant. Il est élégant et volumineux, en forme de triangle symétrique solide et sans fioritures. Ce noeud nécessite une cravate longue et de tissu fin.
Il est complexe à nouer, peu sujet aux erreurs et facile à dénouer.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [CRA]) :
Moyen mnémotechnique : un tour autour de chaque tour et un tour autour des deux tours.
1. Mettre la cravate autour du col, le brin large à votre gauche et le brin étroit un peu au-dessus de la hauteur du nombril.
2. Croiser le brin large au-dessus de le brin étroit.
3. Remonter le brin large et la passer dans la boucle autour du cou.
4. Redescendre le brin large vers votre droite (premier tour autour du tour de cou).
5. Passer le brin large derrière le noeud, vers votre gauche.
6. Remonter le brin large à nouveau et la passer dans la boucle autour du cou.
7. Redescendre le brin large vers votre gauche (deuxième tour autour du tour de cou).
8. Passer le brin large devant le noeud, vers votre droite (tour autour des deux tours précédents).
9. Remonter le brin large pour la troisième fois et la passer dans la boucle le long du cou.
10. Insérer le brin large dans la boucle frontale formée à l'avant du noeud.
11. Serrer le noeud en tirant doucement sur le brin large, puis ajustez-le pour lui donner une forme symétrique et bien triangulaire.
D8.1.26. Noeud carré chinois :
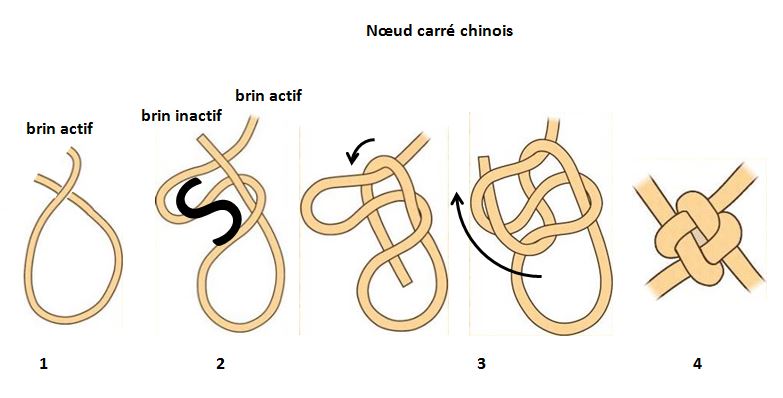
Le noeud carré chinois est un Noeud de décoration Bloquant qui peut être joliment noué sur un foulard.
Il est complexe à nouer, peu sujet aux erreurs et difficile à dénouer.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [SCC][CRE][DAR]) :
1. Croiser un des deux brins du foulard (appelé "actif") sur l'autre brin (appelé "inactif").
2. Avec le brin actif, former un S à deux boucles inversées et trois segments parallèles, le segment inférieur passant au-dessus du brin inactif et les deux autres en dessous.
3. Passer le brin inactif sous les trois segments du S, puis au-dessus du S, et l'insérer dans la boucle supérieure du S.
4. Ajuster le noeud en tirant successivement sur les quatre extrémités des brins.

A noter que ce noeud peut se faire sur soi selon une autre technique pratiquée en scoutisme.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [DAR]) :
1. Croiser à 90° un des deux brins du foulard (appelé "actif") sur l'autre brin (appelé "inactif"), et l'enrouler autour.
2. Placer le doigt sous le noeud derrière le brin inactif et l'enrouler vers l'arrière, ce qui forme une boucle entourant le doigt.
3. Continuer le tour et ramener le brin inactif sur le devant.
4. Passer le brin actif dans la boucle à la place du doigt.
5. Ajuster le noeud en tirant successivement sur les quatre extrémités des brins.
D8.1.27. Noeud de capucin :
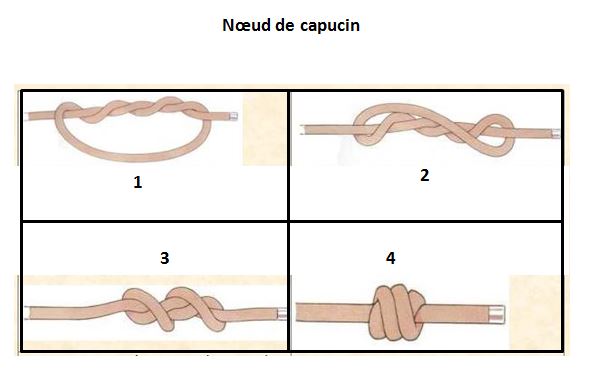
Le noeud de capucin est un Noeud de décoration Semi-coulant, également utilisé comme poignée ou comme lest sur une corde. Il peut supporter de fortes charges ou variables (à-coups)
Il est simple à nouer et difficile à dénouer.
Attention : ce noeud est instable s'il est mal "retourné" ou insuffisamment serré.
Les étapes sont les suivantes (voir Figure ci-dessus, cf. [SCA]) :
1. Faire un Noeud simple mais en passant plusieurs fois le brin libre dans la boucle.
2. Tirer sur les deux brins opposés afin de "retourner" le noeud.
3. Continuer à tirer jusqu'à ce que le noeud soit complètement serré.
4. Vérifier que le noeud se présente comme un cylindre de spires jointives.
A noter qu'un noeud de capucin à deux tours seulement est équivalent à un Noeud simple doublé.
D8.2. Vocabulaire :
Brin courant = Extrémité libre de la corde que l'on manipule pour former le noeud.
Brin dormant = Partie fixe de la corde qui reste immobile pendant la confection du noeud et qui supporte la charge.
Catégorie d'utilisation =
- Noeuds d'arrêt = permettent de bloquer une corde en extrémité afin d'éviter l'effilochage ou le glissement.
- Noeuds de friction (ou autobloquants) = permettent de faire coulisser une corde librement sans charge, tout en assurant un blocage automatique sous charge.
- Noeuds de jonction (ou d'ajut ou d'assemblage de cordes) = permettent de lier deux cordes ensemble.
- Noeuds d'amarrage (ou d'attache) = permettent de fixer une corde à un point fixe (bitte, arbre, anneau, etc.).
- Noeuds de brêlage (ou d'assemblage rigide) = permettent de lier deux pièces rigides ensemble (perches, rondins, etc.) à l'aide d'une corde.
- Noeuds de décoration = permettent de créer des motifs esthétiques.
Clé (terme peu utilisé et sans définition universelle) = Noeud simple dont la boucle entoure totalement le Support, ce dernier pouvant être externe ou interne.
Demi-clé (cf Larousse) = Noeud marin qui consiste, après avoir fait un tour sur un objet quelconque, à faire passer l'extrémité du brin courant sous le brin tendu. L'objet peut être un support externe (bitte, arbre, anneau) ou interne (brin dormant sortant).
Demi-cabestan d'escalade = Noeud de friction sur mousqueton.
Demi-cabestan nautique = Noeud d'amarrage à Tour mort et une seule Demi-clé.
Demi-noeud = Noeud simple. Le demi-noeud est en fait une "moitié" de Noeud plat lorsqu'on concatène virtuellement les deux cordes en un seul cordage continu.
Dénouage = La facilité à dénouer un noeud se définit comme son aptitude à être défait après avoir supporté une forte charge.
Ganse = Boucle d'une corde en forme de U allongé, sans croisement des brins.
Instable = Noeud mal exécuté, donc non fiable et pouvant se défaire spontanément sous charge (sans intervention manuelle).
Nouage = La facilité à nouer un noeud se définit comme son aptitude à être réalisé rapidement et correctement en situation, car reposant sur une chorégraphie spatiale élémentaire des gestes et des brins.
Retournement d'un noeud = Etape qui intervient après avoir enroulé plusieurs tours d'un brin autour d'un autre, comme dans le cas du Noeud de capucin et du Noeud de chirurgien. En tirant simultanément sur les Brins dormants, les tours se réorganisent autour de la partie centrale du noeud, ce qui compacte l'ensemble, modifie la géométrie du noeud et augmente sa friction interne.
Serrage =
- Noeud bloquant : bloque sur le Brin dormant avec ou sans charge, et re-glisse après décharge uniquement sur intervention manuelle (exemple : Noeud en huit d'arrêt).
- Noeud coulant : glisse sur le Brin dormant sans charge, bloque sous charge et re-glisse après décharge uniquement sur intervention manuelle (exemple : Noeud coulant à plusieurs spires).
- Noeud semi-coulant : glisse sur le Brin dormant sans charge, bloque sous charge et re-glisse spontanément (sans intervention manuelle) après décharge (exemple : Noeud de Prusik).
Support d'amarrage = point d'ancrage externe (bitte, arbre, anneau, etc.) ou interne comme une partie de corde (Brin dormant sortant), servant de base fixe pour enroulement du Brin courant lors d'une Demi-clé ou d'une Clé.
Tour mort = Tour complet d'une corde autour d'un Support d'amarrage avant que le Brin courant ne croise le point de départ (Brin dormant), ce qui, dans la pratique, fait souvent un tour et demi de la circonférence du Support (voir Noeud de cabestan).
D8.3. Sources :
[ALP] AlpineSavvy, Using a rope to make a tensionless tree anchor.
[AND] andreba, Noeud papillon alpin (Youtube, 01:45).
[ANI] Animated knots, Clove Hitch - Loops.
[ARN1] ArnO'Voyages, [Tuto'Escalade] Le noeud d'encordement en CHAISE - Comment faire - Quelle utilisation ? (Youtube, 04:08).
[ARN2] ArnO'Voyages, [Tuto'Escalade] Le noeud de jonction - Noeud simple - descente en rappel - Comment faire ? (Youtube 02:52).
[BUD] Budworth Geoffrey, Guide des noeuds, Parragon Books Ltd, 2006.
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[COM] comment_economiser.fr, Le Noeud de Chaise est le Noeud le Plus Utile : Solide, Facile à Faire et à Défaire..
[COR] Cordévasion, Comment faire un noeud de pêcheur double en escalade.
[CRA] E.L. Cravatte, Le noeud Windsor.
[CRE] Les Créatifs, Nouage : une boucle chinoise.
[DAR] Dargis Pierre, Noeud carré (Youtube, 02:05).
[DIM] Dimitri Elledge, Comment faire le noeud d'écoute (+noeud d'écoute double) - Noeud de jonction! (Youtube, 04:45).
[ENA] Enautic, Le Noeud : 1 tour mort et 2 demi clés (Youtube, 00:54).
[FRA] La fraternité du scoutisme, Assemblage du bois.
[GET] gettin, A Cool Guide demonstrating how to Tie a Lasso.
[GRU] Grupo Scout Barrio La Victoria, Nudo rizo.
[KIM] kimoc13, Faire le noeud coulant facilement. (Youtube, 04:30).
[KIN] KINRED, Faire le noeud de chaise avec une main les yeux fermés ! (Youtube, 00:23).
[KNO] knots.neocities.org, Figure 8 Barrel sling.
[LYO] http://lyon.noeuds.free.fr, Les noeuds - Le noeud de cabestan.
[MAG1] Montagnes Magazine, Bien choisir son noeud pour rabouter 2 cordes.
[MAG2] Montagnes Magazine, Comment faire un noeud de jonction de corde ?.
[MAR1] Marsala, Noeud de chirurgien (Youtube, 01:39).
[MAR2] Marsala, Matelotage : Noeud de chirurgien (Youtube, 01:18).
[MAR3] Marsala, Noeud de pecheur simple.MOV (Youtube, 02:08).
[MIN] Minute Forme, Réaliser un noeud double pêcheur (Youtube, 01:57).
[MIS] La Misaine, Noeuds marins.
[MON] Orientacion en el campo y tecnicas de Montanismo - Nudos, amarres y estructuras.
[NAU] Nautisme-pratique.com, le noeud cabestan.
[NOD] Nodo Farfalla (Alpine Butterfly Knot): Tutorial(Youtube, 00:33).
[PEC] Pêche pro, Les noeuds.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[PET] Petzl, Noeuds.
[PIN] Pinterest, Noeud marin.
[PON] Pontonniers de Genève, Cordages.
[QUE] Le Quercus, Les Noeuds de brêlages (Youtube, 25:08).
[REG] Regroupement scout francophone 64e Clarence-Rockland, Brêlage en croix.
[SAI] True Sailor, Noeud tour-mort deux demi-clés.
[SAU] Sauvetage Rivière Boréal, 8 noeuds utiles pour le sauvetage en eau vive et en eaux vives.
[SCA] Science Maison, Noeud de capucin.
[SCC] Science Maison, Noeud carré décoratif.
[SCE] Science Maison, Noeud d'écoute (oeud de tisserand).
[SCO] ScoutWiki, Surliure.
[THE] The Knots Manual, How to Tie a Prusik Knot.
[VOI] Voile & Moteur, Matelotage : Variations sur noeud de chaise.
[WHY] WhyKnot, Apprenez à nouer un lasso de cow-boy (Youtube, 01:49).
[WIK] Wikipedia, Noeud constricteur.
[WIK] Wikipedia, Noeud de papillon alpin.
[WIK] Wikipedia, Noeud de Zeppelin.
Voir détail.

E4.1. Introduction :
La génétique est la science qui étudie l'organisation, le fonctionnement, la régulation et la modification des gènes, tant dans leur transmission d'une génération à l'autre que dans leur expression au sein d'un même individu.
Elle comprend six grands domaines scientifiques [PER][CHA] :
1. Organisation du génome et fabrication cellulaire
Chaque cellule du corps humain possède une copie complète du matériel génétique de l'organisme (le génome), porté par l'ADN (Acide DésoxyriboNucléique).
Ce génome contient toutes les instructions nécessaires à la fabrication de l'ensemble des protéines de l'organisme. Cependant, en pratique, chaque cellule n'exprime qu'une partie des gènes, en fonction de sa spécialisation. Par exemple, une cellule musculaire produira principalement des protéines contractiles, et peu ou pas de protéines spécifiques aux neurones ou aux cellules immunitaires.
Les protéines jouent un rôle essentiel dans l'organisme. D'une part, elles assurent des fonctions structurelles en maintenant et réparant les tissus. D'autre part, elles agissent comme régulateurs des fonctions vitales, en participant notamment à la régulation génétique (histones et facteurs de transcription), hormonale (hormones), digestive (enzymes), au transport de l'oxygène dans le sang (hémoglobine) et à la défense immunitaire (anticorps).
Chaque cellule produit ainsi deux grands types de protéines :
- des protéines effectrices (ou cibles), telles que les protéines structurales, les protéines de transport, les hormones et les enzymes, qui assurent les fonctions cellulaires et physiologiques du corps.
- des protéines régulatrices, telles les histones et les facteurs de transcription, qui contrôlent l'expression des gènes.
Une fois fabriquées, les protéines sont acheminées à leurs lieux d'action (cellules, organes, tissus). Certaines, comme les hormones, voyagent dans le sang pour atteindre des organes éloignés.
2. Régulation génétique
La régulation génétique est le contrôle de l'expression des gènes, notamment par la modulation de l'accessibilité de l'ADN, sans modification de la séquence d'ADN.
Les acteurs principaux de ce mécanisme sont les suivants :
- Les séquences d'ADN non codant (non traduites en protéines) qui sont principalement constituées de Gènes non codants et de Séquences intergéniques.
- Les Protéines régulatrices qui sont de deux types principaux : les Histones assurant le compactage de l'ADN autour d'elles et donc la modulation de son accessibilité, et les Facteurs de transcription venant se fixer sur les séquences d'ADN non codant pour activer ou réprimer l'expression des gènes.
- Les Modifications épigénétiques qui sont des ajouts réversibles de groupes chimiques sur les molécules d'ADN et aussi sur les queues des histones, modifiant l'accessibilité de l'ADN et donc la réponse de l'organisme aux stimuli internes et externes.
- Les ARN longs non codants qui agissent comme régulateurs indirects, par exemple comme guides des protéines vers des régions spécifiques de l'ADN.
3. Variation génétique
La variation génétique est la production des différences génétiques. Les mécanismes principaux sont les suivants :
- Mutation : modification durable de la séquence d'ADN au niveau du gène, du chromosome ou du génome entier.
- Recombinaison (crossing-over) : échange de segment d'ADN entre chromosomes homologues lors de la méiose, créant de nouvelles combinaisons génétiques.
- Polymorphisme : coexistence de plusieurs formes génétiques normales dans une population, comme le montre le système des groupes sanguins ABO chez l'humain qui produit une diversité de groupes (A, B, AB, O, etc.).
- Transposition : changement de position d'un segment d'ADN dans le génome.
- Dérive génétique : changement aléatoire des fréquences des différentes formes d'un gène dans une petite population, souvent dû à des événements fortuits (catastrophes, isolement) qui réduisent le nombre d'individus.
- Migration (ou flux génétique) : déplacement d'individus d'une population vers une autre, entraînant l'arrivée ou le départ de certaines formes de gènes dans la population d'accueil.
- Accouplement aléatoire : reproduction oû les partenaires sont choisis au hasard, favorisant le brassage génétique dans la population.
4. Réparation génétique
La réparation génétique est la correction des erreurs ou des dommages dans l'ADN. Les mécanismes principaux, classés par gravité croissante des lésions, sont les suivants :
- Réparation directe (Direct repair) : pour une base peu endommagée
- Réparation par excision de base (BER) : pour une base absente ou fortement endommagée
- Réparation des erreurs de copie (MMR) : pour une séquence erronée suite à la réplication de l'ADN
- Réparation par excision de nucléotides (NER) : pour une séquence endommagée
- Réparation de cassures simple brin (SSB repair) : pour un brin cassé, avec le second brin intact servant de modèle
- Réparation de cassures double brin (DSB repair) : pour un double brin cassé
5. Transmission génétique
La transmission génétique est la transmission de l'information héréditaire au niveau individuel (entre cellules d'un même organisme) ou transgénérationnel (d'une génération à l'autre). Les mécanismes principaux sont les suivants :
- Réplication : copie fidèle de l'ADN avant chaque division cellulaire.
- Mitose : division cellulaire de cellules somatiques (corporelles) produisant deux cellules filles identiques avec le même nombre de chromosomes que celui de la cellule mère.
- Méiose : division cellulaire de cellules germinales (reproductrices) produisant deux gamètes (ovule et spermatozoïde) contenant chacun la moitié du nombre de chromosomes. Cette division ne fragmente pas l'information génétique mais la redistribue intelligemment entre les gamètes grâce à des mécanismes de brassage et de contrôle, permettant à la fécondation de reconstituter un patrimoine génétique complet et unique.
- Fécondation : fusion de deux gamètes pour former une cellule-oeuf (zygote) à nombre complet de chromosomes.
- Transmission Mendélienne : transmission de caractères héréditaires via des gènes situés sur les chromosomes nucléaires (donc hérités des deux parents), selon les lois de Mendel.
- Transmission non Mendélienne : transmission de caractères héréditaires ne suivant pas les lois de Mendel, soit en raison de la localisation des gènes situés en dehors des chromosomes nucléaires (comme l'ADN mitochondrial hérité uniquement de la mère, ou l'ADN chloroplastique), soit en raison de mécanismes particuliers affectant les gènes nucléaires (comme l'empreinte parentale, la dominance incomplète, la mutation dynamique, la liaison au sexe).
- Transmission épigénétique : transmission, au niveau individuel ou transgénérationnel, des marques de régulation de l'expression des gènes, sans modification de la séquence d'ADN.
6. Sélection naturelle
La sélection naturelle est un mécanisme d'évolution qui trie les individus selon leur aptitude à survivre et à se reproduire.
compte tenu des variations héréditaires entre individus, la sélection naturelle favorise certains traits parmi cette diversité : les individus porteurs de caractères génétiques avantageux pour leur survie et leur reproduction, dans un environnement donné, produisent davantage de descendants.
Ce concept de sélection naturelle a évolué historiquement selon quatre temps (illustré par la girafe) :
- Lamarck (hérédité des caractères acquis, 1809) :
La girafe allonge son cou pour atteindre les feuilles en hauteur et transmet ce caractère acquis à ses descendants.
- Darwin (sélection naturelle, 1859) :
Chez les girafes, celles qui naissent avec un cou plus long par variations individuelles fortuites survivent mieux et se reproduisent davantage, produisant ainsi plus de descendants.
- Néo-darwinisme (génétique moderne, Collectif, 1930-1940) :
Chez les girafes, celles qui naissent avec un cou plus long en raison de mutations génétiques aléatoires (non dirigées par l'environnement) survivent mieux et se reproduisent davantage, produisant ainsi plus de descendants.
- Epigénétique (régulation de l'expression des gènes, Waddington, 1942) : Chez les girafes, en plus des mutations génétiques aléatoires, la difficulté à atteindre les feuilles en hauteur pourrait modifier l'expression des gènes impliqués dans la croissance du cou, sans changer la séquence de l'ADN. Ces modifications épigénétiques pourraient être temporairement transmises à leurs descendants.
En synthèse :
Le fonctionnement cellulaire, à travers ces grandes fonctions (organisation, fabrication, régulation, variation, réparation, transmission), illustre avec finesse l'équilibre dynamique entre assimilation et accommodation, tel que décrit par Jean Piaget.
A l'image de l'intelligence du vivant qui ajuste sans cesse ses schèmes pour intégrer ou transformer l'expérience, la cellule assimile la plupart des événements selon ses programmes génétiques et épigénétiques. Mais elle sait aussi accommoder, c'est-à-dire ajuster ou remodeler ses mécanismes, face à la nouveauté ou à la perturbation.
Cet équilibre adaptatif, moteur de la plasticité cellulaire, fournit à plus grande échelle les innovations sur lesquelles agit la sélection naturelle.
E4.2. Description de la cellule :
Une description hiérarchique de la cellule eucaryote (avec noyau) est donnée comme suit [PER][CHA] :
Nota : Le nombre indiqué est relatif à l'être humain adulte.
Cellule eucaryote = Membrane plasmique + Cytoplasme + Noyau. Nombre = 37 000 milliards
|
| Membrane plasmique = enveloppe séparant l'intérieur et l'extérieur de la cellule.
|
| Cytoplasme = Cytosol + Organites
| | Cytosol = milieu aqueux contenant ions, nutriments et enzymes.
| | Organites = Ribosomes libres + Réticulum endoplasmique + Mitochondries + Appareil de Golgi + Lysosomes + Cytosquelette
| | | Ribosomes libres = synthétisent les protéines à partir de l'ARN messager. Nombre = 10 millions
| | | Réticulum endoplasmique (RE) = synthétise les lipides (RE lisse) et d'autres protéines (RE rugueux, pourvu de Ribosomes fixés).
| | | Mitochondries = produisent l'énergie cellulaire (ATP) par respiration cellulaire. Contiennent leur propre ADN (génome mitochondrial). Nombre = 100 à 10 000 (selon type de cellule).
| | | Appareil de Golgi = trie, emballe et transporte les molécules (protéines et lipides principalement) vers leur destination finale (en interne ou externe à la cellule).
| | | Lysosomes = digèrent les déchets cellulaires. Nombre = 300 à 500
| | | Cytosquelette = maintient la forme celulaire et participe aux mouvements cellulaires.
|
| Noyau = Membrane nucléaire + Nucléoplame + Chromatine + Nucléoles
| |
| | Membrane nucléaire = enveloppe double séparant l'intérieur et l'extérieur du Noyau.
| |
| | Nucléoplame = milieu gélatineux contenant enzymes et ions.
| |
| | Chromatine = Génome nucléaire + Protéines régulatrices + ARN associés + Modifications épigénétiques
| | |
| | | Génome nucléaire = ensemble de Chromosomes. Nombre = 23 paires de chromosomes.
| | | | Chromosome = Molécule d'ADN compactée (double hélice constituée de deux brins antiparallèles de Nucléotides) = Gènes codants + Gènes non codants + Séquences intergéniques
| | | | | Gène codant = séquence d'ADN contenant l'information nécessaire à la synthèse d'une protéine. Nombre = 20 000 gènes codants par génome nucléaire.
| | | | | Gène non codant = séquence d'ADN contenant l'information nécessaire principalement à la synthèse d'un ARN fonctionnel.
| | | | | Séquences intergéniques = séquences d'ADN non codant situées entre deux gènes adjacents (codants ou non codants). Elles constituent notamment les plates-formes d'ancrage pour les Protéines régulatrices et comprennent aussi une diversité de séquences répétées. Proportion = 90 % du génome nucléaire.
| | | | | Nucléotide = Groupement phosphate + Sucre désoxyribose + Base azotée. Nombre = plusieurs millions par Chromosome
| | | | | | Base azotée = Adénine (A), Thymine (T), Cytosine(C) ou Guanine(G). Nombre = 3 milliards de paires de bases azotées par génome nucléaire.
| | |
| | | Protéines régulatrices = Histones + Facteurs de transcription
| | | | Histones = protéines assurant le compactage de l'ADN autour d'elles et donc la modulation de son accessibilité.
| | | | Facteurs de transcription = protéines venant se fixer sur les séquences d'ADN non codant pour activer ou réprimer l'expression des gènes.
| | |
| | | ARN associés = principaux médiateurs de l'expression des gènes.
| | | | ARN messager (ARNm) = copie un Gène codant (le plan de fabrication des protéines) et le transporte jusqu'aux Ribosomes.
| | | | ARN de transfert (ARNt) = transporte les acides aminés vers les Ribosomes et les positionne selon le plan fourni.
| | | | ARN ribosomal (ARNr) = constitue l'ossature des Ribosomes et assemble les acides aminés en chaînes protéiques selon le plan fourni.
| | | | microARN = bloque des ARN messager spécifiques, empêchant leur traduction et réduisant ainsi la production de protéines effectrices.
| | | | ARN long non codant (IncARN) = agit comme régulateur indirect, par exemple comme guide des protéines vers des régions spécifiques de l'ADN.
| | |
| | | Modifications épigénétiques = ajouts réversibles de groupes chimiques sur les molécules d'ADN et sur les histones, modifiant ainsi l'accessibilité de l'ADN.
| |
| | Nucléoles = synthétisent les ARN ribosomaux. Nombre = 1 à 5
E4.3. Epigénétique :
L'épigénétique constitue une sous-couche biologique commune à tous les apprentissages basés sur l'acquisition (stabilisation de la mémoire, plasticité cérébrale, adaptations métaboliques). Elle permet aux cellules de coder l'expérience vécue par des modifications de l'expression des gènes sans altérer la séquence d'ADN, contrairement aux mutations génétiques.
Ce mécanisme fondamental régule dynamiquement l'expression des gènes en fonction du contexte physiologique ou environnemental, permettant ainsi à l'organisme de s'adapter efficacement aux stimuli internes et externes, tels que :
- variations climatiques (température, humidité)
- changements alimentaires (carence, excès, qualité nutritionnelle)
- modifications d'habitat (urbanisation, pollution, migration)
- stress physiologique (maladie, exercice intense)
- stress traumatique (choc émotionnel, violence)
Cette régulation s'effectue par des modifications chimiques réversibles, telles que :
- la méthylation de l'ADN, par ajout de groupes méthyle sur l'ADN.
- la modification de protéines régulatrices (histones principalement) autour desquelles l'ADN s'enroule.
Ces modifications contrôlent dynamiquement l'accès aux gènes et leur niveau d'expression, permettant leur activation ou leur répression, sans altérer le contenu génétique sous-jacent.
Deux niveaux de plasticité sont distingués :
Plasticité individuelle : lorsque les stimuli sont modérés ou transitoires, les modifications restent confinées aux cellules somatiques (corporelles) et ne sont pas transmises aux générations suivantes.
Par exemple :
- Le renard arctique change de pelage (blanc en hiver et brun en été). Les renardeaux naissent avec un pelage adapté à leur saison de naissance, mais leur capacité à changer de couleur dépend ensuite des stimuli environnementaux (étude de Zimova M., Mills L.S., Nowak J.J., 2016).
- Chez l'humain, le bronzage de la peau en réponse au soleil est une adaptation temporaire propre à chaque individu (étude de Slominski A., 2004).
Plasticité transgénérationnelle : lorsque les stimuli sont intenses ou prolongés, les modifications affectent également les cellules germinales (spermatozoïdes et ovocytes). Ces marques sont alors transmises aux descendants et influencent leurs phénotypes (traits comportementaux, physiologiques et morphologiques) sur une à trois générations avant de s'estomper.
Par exemple :
- Chez la puce d'eau (daphnie), l'exposition des parents à des signaux de prédateurs induit chez la descendance le développement de défenses morphologiques (casques ou pointes), même si les jeunes n'ont jamais rencontré de prédateur eux-mêmes (étude de Tollrian R., 1995).
- Des souris mâles exposées durablement au froid donnent naissance à des descendants mieux adaptés aux basses températures (étude de Chan J.C., 2020).
- Des souris mâles conditionnées à craindre une odeur transmettent à leur descendance une hypersensibilité spécifique à cette odeur (étude de Dias B.G., Ressler K.J., 2014).
- Chez l'humain, la malnutrition avant la grossesse chez la mère ou chez le père peut affecter durablement la santé de l'enfant, même si ce dernier grandit ensuite dans un environnement alimentaire normal (étude de Gete DG., Waller M., Mishra GD., 2020).
Dans le cas de l'apprentissage cognitif, l'épigénétique est intimement couplée avec la plasticité cérébrale (réseaux de neurones) selon deux niveaux de codage complémentaires [MER] :
- Un niveau structurel : l'apprentissage modifie la force et l'organisation des connexions synaptiques entre neurones, assurant le stockage et la consolidation des informations acquises (mémoire).
- Un niveau biologique : l'apprentissage induit des modifications épigénétiques dans le génome des cellules neuronales, qui régulent l'expression des gènes impliqués dans la plasticité synaptique et la stabilisation des réseaux neuronaux.
Attention : malgré l'impact profond de l'activité cognitive intensive (comme la pratique musicale) sur la plasticité cérébrale et l'épigénétique neuronale, ces modifications restent strictement individuelles. A ce jour, aucun mécanisme héréditaire, génétique ou épigénétique, n'a été démontré pour transmettre ces adaptations à la descendance.
E4.4. ARN :
L'ARN (Acide RiboNucléique) est le relais dynamique entre l'ADN et l'ensemble des activités cellulaires, assurant à la fois la transmission, la traduction et la régulation de l'information génétique au sein de la cellule.
Tous les ARN sont fabriqués par copie directe (transcription) de séquences d'ADN présent dans le noyau cellulaire, grâce à l'action de l'ARN polymérase, une protéine particulière présente initialement dans la cellule et produite ensuite par l'ARN messager, comme toutes les autres protéines.
Attention : aucun ARN n'est une protéine. L'ARN polymérase, malgré son nom, n'est pas un ARN mais une protéine (enzyme) qui fabrique les ARN.
Un type particulier d'ARN, l'ARN messager (ARNm), est une copie partielle et ciblée de l'information génétique, transmise ensuite aux ribosomes (dans le cytoplasme cellulaire). Ceux-ci "lisent" alors cet ARN messager (ARN codant) comme un plan d'instructions pour fabriquer (synthétiser) les protéines.
D'autres types d'ARN, dits non codants, ne contribuent pas à la fabrication des protéines. Ils sont fonctionnels et remplissent des fonctions régulatrices clés, telles que :
- Bloquer des ARN messager spécifiques pour empêcher leur traduction (par exemple, les microARN), réduisant ainsi la production de protéines effectrices.
- Contrôler l'accès à l'ADN via des modifications épigénétiques (par exemple, les ARN longs non codants), modulant ainsi l'expression des gènes sans altérer la séquence d'ADN.
E4.5. Sources relatives à la génétique :
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[MER] Karine Merienne, Anne-Laurence Boutillier, Régulations épigénétiques et plasticité cérébrale : vers de nouvelles thérapies dans les maladies neurodégénératives ?, 2016.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
Voir détail.
 Dernière mise à jour de la page : 22 février 2026
Dernière mise à jour de la page : 22 février 2026