
| In English | Accueil/Contact | Billard | Bélier | SNH | Relativité | Botanique | Musique | Ornitho | Météo | Aide |

Cette page est destinée aux amoureux de la musique et aux curieux de la science musicale.
Au-delà des aspects bien connus des Sons musicaux (Gamme, Hauteur, Consonance, Timbre, etc.), cette page présente quelques aspects moins connus de leur rapport avec la perception humaine (Psychoacoustique) et le Langage parlé (Sons de type Syllabe).
Cette page comporte également un Lexique détaillé des termes utilisés en Musique, Acoustique et Langage parlé.
Notations de cette page :
- Les mots-clés ont leur première lettre indiquée en majuscule et sont définis dans le Lexique.
- Les auteurs cités sont mentionnés entre crochets sous la forme [AUTEUR Titre Page]. Voir Bibliographie.

La notation musicale a pour but de recenser et d'expliquer tous les symboles utilisés dans une partition de musique.
Ces symboles peuvent se classer en deux domaines : la Mélodie et le Rythme (voir [TOS]).
La Mélodie est l'organisation en Hauteur des événements musicaux. Elle est caractérisée essentiellement par :
- la Portée,
- la Hauteur des Notes (Nom des Notes, Clef, Altération, Intervalle, Accord, Son musical),
- la Structure mélodique (Nuance, Liaison, Ornement),
- la Tessiture des Instruments.
Le Rythme est l'organisation temporelle des événements musicaux. Il est caractérisé essentiellement par :
- les Durées (Figure de Note, Figure de Silence, Durée d'une Note, Durée d'un Silence, Liaison, Ornement),
- les Mesures (Barre de Mesure, Chiffrage de Mesure),
- les Répétitions de Temps, de Mesures, de sections ou de morceaux,
- le Tempo,
- le Caractère,
- les Rythmes parfois Irrationnels.
Certains Instruments (notamment : Guitare, Basse et Batterie) ont une notation spécifique liée à la pratique de la musique Jazz/Rock. La plupart des symboles employés sont les symboles standards mais détournés de leur signification habituelle pour s'adapter au contexte de l'Instrument. On peut se reporter à ce sujet au livre [TOS].
La Gamme diatonique est une échelle de Sons musicaux à sept Degrés, qui est à la base de la musique savante occidentale héritée de la musique grecque antique, stabilisée par le chant liturgique et la musique modale médiévale, et fixée formellement par la polyphonie de la Renaissance.
Sa construction a fait l'objet de trois approches successives marquantes : l'approche psychoacoustique des Anciens, l'approche mathématique de Pythagore et l'approche pragmatique "tempérée".
En particulier, les deux premières approches expliquent simplement pourquoi il n'y a qu'un Demi-ton entre les Notes mi - fa et si - do.
Pourquoi le piano a-t-il sept touches blanches et deux groupes distincts de touches noires ?
Le piano réel offre un avantage essentiel par rapport à un piano fictif à 6 touches blanches et 6 touches noires : les touches noires sont disposées tout le long du clavier en deux groupes, l'un de deux touches, l'autre de trois touches. Cette organisation optimale permet rapidement de situer, visuellement et tactilement, une Note, qu'elle soit altérée ou non, dans une octave donnée, ce qui facilite grandement l'orientation sur le clavier, la précision du doigté et l'exécution fluide de toutes les figures musicales telles que sauts d'Octaves, Arpèges, Accords et passages complexes.

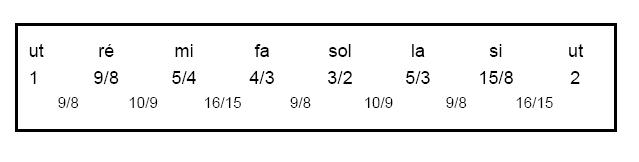
Figure 1 ci-dessus : Les douze premiers harmoniques de do2, montrant sept motifs sonores remarquables présents dans les six premiers harmoniques.
Figure 2 ci-dessus : Gamme diatonique majeure de Zarlino. La première ligne donne les rapports de fréquences des notes par rapport au do de départ. La seconde ligne donne les rapports de fréquences entre notes conjointes.
Dans presque tous les pays du monde, la Gamme rudimentaire est basée sur trois Intervalles qui sont : l'Octave, la Quinte et la Quarte.
Le système auditif humain a ainsi une prédisposition à traiter préférentiellement les Intervalles basés sur des rapports de Fréquences simples, en l'occurrence : 2/1, 3/2 et 4/3.
Cette prédisposition serait, non pas innée, mais acquise très jeune par l'exposition aux Sons harmoniques tels que ceux de la voix humaine (cf [GOY]).
En plaçant ces trois Intervalles sur une même Note (que nous appellerons do par commodité), il devient alors simple d'expliquer la formation de la Gamme diatonique comme suit (cf [LAV]) :
Trois Sons musicaux sont déjà posés :
- le do à l'Octave (Intervalle de rapport 2/1 correspondant à l'Octave),
- le sol (Intervalle de rapport 3/2 correspondant à la Quinte),
- le fa (Intervalle de rapport 4/3 correspondant à la Quarte).
Il est alors fort probable (sans que cela soit prouvé scientifiquement à ce jour) que l'oreille humaine se comporte comme un extracteur de Spectre sonore et entend les Sons musicaux en les Décomposant en série de Fourier sous forme d'une somme d'ondes sinusoïdales dont les Fréquences sont des multiples entiers d'une même Fréquence appelée Fondamentale (voir Figure 1 ci-dessus, exemple du do2).
Si f est la Fréquence Fondamentale du do de base, ses Harmoniques (depuis le rang 1) sont alors les suivantes : f, 2f, 3f, 4f, 5f, 6f, etc.
En entendant chacun des trois sons posés précédemment, une oreille exercée entend donc également leurs Harmoniques respectives.
En se limitant aux six premiers Harmoniques de chaque son (l'intensité des Harmoniques supérieures (7f, 8f, etc.) décroissant rapidement pour la plupart des sons musicaux), l'oreille entend alors l'ensemble des Fréquences suivantes :
- pour le do à l'Octave : (2/1)f, 4f, 6f, 8f, 10f, 12f, correspondant aux Notes Fondamentales : do (f), do (f), sol (3/2 f), do (f), mi (5/4 f), sol (3/2 f)
- pour le sol : (3/2)f, 3f, (9/2)f, 6f, (15/2)f, 9f, correspondant aux Notes Fondamentales : sol (3/2 f), sol (3/2 f), ré (9/8 f), sol (3/2 f), si (15/8 f), ré (9/8 f)
- pour le fa : (4/3)f, (8/3)f, 4f, (16/3)f, (20/3)f, 8f, correspondant aux Notes Fondamentales : fa (4/3 f), fa (4/3 f), do (f), fa (4/3 f), la (5/3 f), do (f)
Les Fréquences ont été toutes normalisées en les divisant par 2 autant de fois que nécessaire pour les ramener dans l'Octave.
Ces trois groupes de Notes font alors apparaître quatre nouvelles Notes : ré, la, mi, si.
On obtient ainsi toutes les Notes d'une Gamme Majeure parfaitement juste (voir Figure 2 ci-dessus) : do (f), ré (9/8 f), mi (5/4 f), fa (4/3 f), sol (3/2 f), la (5/3 f), si (15/8 f), do (2f).
On peut présenter aussi la Gamme de Zarlino comme résultant de l'enchaînement de trois Quintes Pures fa - do - sol - ré, chaque Quinte Pure (rapport 3/2) étant meublée par une Note formant Tierce majeure Pure (rapport 5/4) avec la Note grave de la Quinte (fa la do ; do mi sol ; sol si ré).
Cette Gamme naturelle (appelée Gamme de Zarlino et parfois "Gamme naturelle") a été explicitée au 16e siècle par Gioseffo Zarlino, prêtre et musicien italien, non pas selon cette approche fondée sur les Harmoniques mais sur une construction numérologique par divisions successives.
Les trois Sons musicaux do, sol et fa contiennent chacun, dans leurs Harmoniques de rang 4, 5 et 6, la Triade suivante :
- le do contient la Triade "do - mi - sol",
- le sol contient la Triade "sol - si - ré",
- le fa contient la Triade "fa - la - do".
Chacune des ces Triades est un Accord parfait majeur, empilement de deux Tierces dont la plus grave est Majeure (rapport 5/4), la plus haute Mineure (rapport 6/5), les deux Notes extrêmes étant à distance de Quinte (rapport 3/2).
Par ailleurs, chacun de ces Accords se trouve renforcé en intensité par les trois premiers Harmoniques du Son musical. On peut en effet constater que :
- les rangs 1 et 2 "répètent" la même Note que la Note la plus grave de l'Accord (rang 4).
- le rang 3 "répète" la même Note que la Note la plus aigüe de l'Accord (rang 6).
Au total, une oreille exercée peut percevoir un Accord parfait majeur dans chacun des trois Sons musicaux do, sol et fa entendus isolément.
Cette perception implique d'avoir nécessairement :
- deux Tons entre les Notes do - mi, sol - si et fa - la (correspondant à la Tierce majeure de rapport 5/4),
- un Ton augmenté d'un Demi-ton entre les Notes mi - sol, si - ré et la - do (correspondant à la Tierce mineure de rapport 6/5).
|
Cette approche Psychoacoustique explique pourquoi il n'y a qu'un Demi-ton entre les Notes mi - fa et si - do, seule combinaison permettant d'obtenir à la fois les trois résultats suivants : - Perception d'un Accord parfait majeur dans chacun des trois Sons musicaux do, sol et fa entendus isolément, à savoir : "do - mi - sol" pour le do de base, "sol - si - ré" pour le sol de base, et fa - la - do pour le fa de base. - Construction d'une Gamme diatonique dont l'ensemble des couples de Notes conjointes ne comporte que deux seuls rapports de Fréquences entre Notes : le Ton et le Demi-ton. - Construction d'une Gamme diatonique dont les Demi-tons sont minoritaires par rapport aux Tons. Démonstration : Si rn désigne le rapport de Fréquences entre deux Notes conjointes d'indice n (r1 entre do et ré, r2 entre ré et mi, ..., r7 entre si et do), alors la perception de ces trois Accords parfaits majeurs induit les relations suivantes : Accord parfait majeur "do - mi - sol" : r1 r2 = 5/4 et r3 r4 = 6/5 Accord parfait majeur "sol - si - ré" : r5 r6 = 5/4 et r7 r1 = 6/5 Accord parfait majeur "fa - la - do" : r4 r5 = 5/4 et r6 r7 = 6/5 Ces six relations sont équivalentes à : r1 = r4 = r6 r2 = r5 = (5/4)/r1 r3 = r7 = (6/5)/r1 Lorsque les rapports de Fréquences r1, r2 et r3 sont tous trois différents, on retrouve la gamme de Zarlino. En revanche, si l'on souhaite construire une gamme diatonique à deux seuls rapports de Fréquences, alors il est nécessaire que r2 = r1 ou r3 = r1. Le premier cas (r2 = r1) induit que : r1 = (5/4)1/2 avec les résultats suivants : r1 = r2 = r4 = r5 = r6 = (5/4)1/2 = 1,118 correspondant à une largeur de 0,16 Octave (= log2(1,118)) r3 = r7 = (24/25) r1 = (24/25) (5/4)1/2 = 1,073 correspondant à une largeur de 0,10 Octave Si on considère qu'il y a un Demi-ton entre les Notes mi - fa (rapport r3) et si - do (rapport r7), il y a donc un même Ton pour chacun des autres rapports. Le second cas (r3 = r1) induit que : r1 = (6/5)1/2 avec les résultats suivants : r1 = r3 = r4 = r6 = r7 = (6/5)1/2 = 1,095 correspondant à une largeur de 0,13 Octave r2 = r5 = (25/24) r1 = (25/24) (6/5)1/2 = 1,141 correspondant à une largeur de 0,19 Octave Si on considère qu'il y a un Ton entre les Notes ré - mi (rapport r2) et sol - la (rapport r5), il y a donc un même Demi-ton pour chacun des autres rapports. Si l'on souhaite construire une Gamme diatonique dont les Demi-tons sont minoritaires par rapport aux Tons, alors seul le premier cas convient, ce qui explique pourquoi il n'y a qu'un Demi-ton entre les Notes mi - fa et si - do. |
L'ensemble des trois groupes de Notes Fondamentales prises ensemble a la caractéristique suivante :
- le do y figure 5 fois,
- le sol y figure 5 fois,
- le fa y figure 3 fois,
- le ré y figure 2 fois,
- le la y figure 1 fois,
- le mi y figure 1 fois,
- le si y figure 1 fois.
Ainsi, l'ordre d'importance de ces sept Notes est identique à celui des Fonctions Tonales qui prolongent la notion de Degré en Musique tonale.
Pour construire le reste de la gamme de Zarlino (Notes Altérées), les sept Notes précédentes sont conventionnellement complétées d'une Tierce majeure Pure (rapport 5/4) ascendante et descendante, le fa Dièse étant à la Tierce ascendante du ré, le mi Bémol à la Tierce descendante du sol, et ainsi de suite.
Les nouvelles Notes obtenues servent ensuite à produire les Notes Altérées restantes selon le même procédé, par exemple le la Dièse étant à la Tierce ascendante du fa Dièse.
Ce qui donne au total :
Suite obtenue par procédé ascendant : do, do#, ré, ré#, mi, mi#, fa, fa#, sol, sol#, la, la#, si, si#, do
Suite obtenue par procédé descendant : do, réb, ré, mib, mi, fab, fa, solb, sol, lab, la, sib, si, dob, do
On voit apparaître alors deux sortes de Demi-tons diatoniques :
- le petit diaton de rapport 16/15 (do - réb, ré - mib, ré# - mi, mi - fa, fa# - sol, sol - lab, sol# - la, la# - si, si - do),
- le grand diaton de rapport 27/25 (do# - ré, la - sib, fa - solb),
ainsi que deux sortes de Demi-tons chromatiques :
- le petit chromate de rapport 25/24 (do - do#, dob - do, ré - ré#, mi - mi#, mib - mi, fab - fa, sol - sol#, solb - sol, lab - la, si - si#, sib - si),
- le grand chromate de rapport 135/128 (réb - ré, fa - fa#, la - la#).
Voir synthèse dans Intervalles.
|
Dans la Gamme de Zarlino, les Intervalles entre Notes Conjointes présentent trois mêmes rapports : 9/8, 10/9 et 16/15, appelées Ton majeur, Ton mineur et Demi-ton diatonique (voir Figure 2 ci-dessus). - L'alternance des intervalles selon le schéma MNDMNMD (M = Ton majeur, N = Ton mineur, D = Demi-tons) est donc une conséquence inévitable du fait que les notes proviennent du spectre harmonique des notes de base do (2/1), sol (3/2) et fa (4/3) correspondant respectivement à l'Octave, la Quinte juste et la quarte juste. - L'Intervalle du Ton majeur au Ton mineur vaut 81/80 et s'appelle Comma zarlinien ou syntonique. Cette différence, quoique petite, reste cependant perceptible à l'oreille et peut être source de Dissonances. - En plus de cette différence, les Tons et les Demi-tons sont spécifiques à chaque position, ce qui rend la Transposition quasi-impossible. - Toutes ces raisons font que la Gamme de Zarlino est très peu utilisée par les compositeurs. - Cette Gamme reste néanmoins utile lorsqu'un groupe vocal (choristes) ou un groupe de violonistes interprète une musique polyphonique Consonante et souhaite provoquer au niveau des auditeurs une sensation de perfection que l'on n'a pas avec un Instrument accordé en Gamme tempérée. Par ailleurs, une oreille exercée peut percevoir un Accord parfait majeur dans chacun des trois Sons musicaux do, sol et fa entendus isolément (voir Perception de trois Accords parfaits majeurs). Cette approche Psychoacoustique explique pourquoi il n'y a qu'un Demi-ton entre les Notes mi - fa et si - do. Plus globalement, l'analyse harmonique réalisée sur les trois Sons musicaux do, sol et fa s'applique également à tout Son musical dans la mesure où il est périodique, donc décomposable en séries de Fourier. Il est donc fort probable que l'oreille humaine soit constamment habituée à percevoir (consciemment ou inconsciemment) les motifs sonores suivants présents dans les six premiers Harmoniques de tout Son musical, f étant sa Fréquence Fondamentale (voir Figure 1 ci-dessus) : - l'Octave (Intervalle entre 2f et f (rapport 2/1), par exemple : do - do à l'Octave) ; - la Quinte à l'Octave (Intervalle entre 3f et f, ou entre 6f et f, ramené à l'Octave (rapport 3/2), par exemple : do - sol) ; - la Quarte à l'Octave (Intervalle entre 4f et 3f (rapport 4/3), par exemple : sol - do à l'Octave, ou do - fa) ; - la Tierce majeure à l'Octave double (Intervalle entre 5f et f, ramené à l'Octave (rapport 5/4), par exemple : do - mi) ; - la Tierce mineure à l'Octave (Intervalle entre 6f et 5f (rapport 6/5), par exemple : mi - sol) ; - la Sixte majeure à l'Octave double (Intervalle entre 5f et 3f (rapport 5/3), par exemple : sol - mi à l'Octave, ou do - la) ; - l'Accord parfait majeur à l'Octave double (Triade 4f, 5f, 6f, par exemple : do - mi - sol). A noter que l'oreille identifie plus naturellement une harmonique ramenée à l'Octave de la Fondamentale (par exemple Tierce majeure entre 5f et f) qu'elle ne perçoit le rapport brut entre deux harmoniques adjacentes (par exemple Tierce majeure entre 5f et 4f). A noter également que la Quarte est moins perçue acoustiquement que logiquement sous forme de Quinte Renversée. |
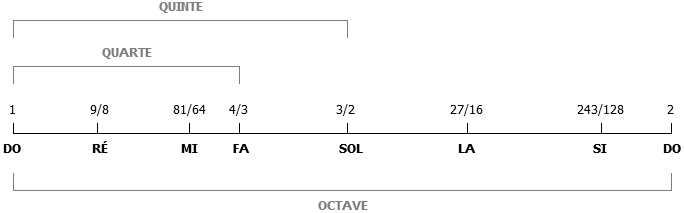

Figures ci-dessus : Gamme diatonique majeure de Pythagore. Le premier axe horizontal donne les rapports de fréquences des notes par rapport au do de départ. Le second axe donne les rapports de fréquences entre notes conjointes.
Au 6e siècle avant J.-C., Pythagore a construit mathématiquement sa Gamme diatonique Majeure en trois étapes :
Etape 1 : l'Octave et le do (cf [MAN])
Voir premier axe en Figure ci-dessus (OCTAVE).
Pythagore prend une corde tendue et la fait vibrer. En la divisant par deux, il s'aperçoit qu'elle vibre à l' Octave (la Fréquence est un multiple de 2 et la Note est identique). Il construit alors l'Intervalle do - do avec le second do à l'Octave (rapport 2/1).
Etape 2 : les cinq Notes ré, mi, sol, la et si (cf [MAN])
Voir premier axe en Figure ci-dessus (QUINTE et autres Notes sauf le FA).
En pinçant les deux tiers de la corde, Pythagore obtient la Quinte (rapport 3/2) et construit le sol. En itérant le principe de la Quinte, il construit le ré (rapport 3/2 x 3/2 = 9/4, que l'on divise par 2 pour normaliser, soit 9/8) puis le la (rapport 9/8 x 3/2 = 27/16) puis le mi (rapport 27/16 x 3/2 = 81/32, que l'on divise par 2, soit 81/64) puis le si (rapport 81/64 x 3/2 = 243/128) puis une Note intermédiaire (rapport 243/128 x 3/2 = 729/256, que l'on divise par 2, soit 729/512). L'itération suivante donne à nouveau le do (rapport 729/512 x 3/2 = 2187/1024, que l'on divise par 2, soit 2187/2048 = 1,068) mais avec un léger décalage par rapport au do du départ.
Il aurait pu continuer mais il s'arrête à sept Notes, probablement parce que ce nombre est celui des astres connus à son époque.
Etape 3 : la Note fa
Voir premier axe en Figure ci-dessus (QUARTE).
La Note intermédiaire (rapport 729/512 correspondant en fait au fa#) n'est pas conservée par Pythagore mais remplacée par 4/3 qui rend la gamme musicalement harmonieuse. Cette valeur 4/3 correspond en effet à la Quarte obtenue en pinçant les trois quarts de la corde et aussi à la "Quinte Renversée" qui est le complémentaire de la Quinte dans l'Octave (4/3 x 3/2 = 2). Ce remplacement ne fait que remplacer localement la paire ton (mi - fa#) - demi-ton (fa# - sol) par la paire inverse demi-ton (mi - fa) - ton (fa - sol), sans toucher au reste des divisions de la gamme. Pythagore construit ainsi le fa.
En réorganisant les Notes par Fréquences croissantes, la Figure ci-dessus donne alors toutes les Notes de la Gamme diatonique : do, ré, mi, fa, sol, la, si, do, qui se trouvent séparées par seulement deux types d'écarts : le ton (rapport 9/8) et le demi-ton (rapport 256/243). Voir second axe en Figure ci-dessus.
Pour construire le reste de la gamme de Pythagore (Notes Altérées), on prolonge les itérations de 7 Quintes jusqu'à 12 Quintes, ce qui fait apparaître sept nouvelles Notes diésées dans la suite des Quintes ascendantes : do - sol - ré - la - mi - si - fa# - do# - sol# - ré# - la# - mi# - si# (principe du Cycle des Quintes, mais en Gamme non Tempérée).
Si le do initial a pour Fréquence f, alors le do final après 12 Quintes justes aura la Fréquence ((3/2)12/27) f = 1,0136 f correspondant à la différence entre 12 Quintes justes et 7 Octaves. Ce léger écart s'appelle comma pythagoricien correspondant exactement à l'écart entre le do# et le réb dans le système pythagoricien. Il correspond également à l'écart minimum existant entre une puissance de 3/2 et une puissance de 2 lorsqu'on prolonge indéfiniment le cycle des Quintes.
Pour former l'Octave juste, on diminue alors la dernière Quinte, laquelle devient très Dissonante ("hurlante") malgré ce très léger décalage, et s'appelle à juste titre "Quinte du loup".
La suite des Quintes descendantes depuis le do initial fait, par ailleurs, apparaître le fa ainsi que onze nouvelles Notes bémolisées : do - fa - sib - mib - lab - réb - solb - dob - fab - sibb - mibb - labb - rébb
A noter que les Notes bémolisées doubles sont des variantes approchantes de Notes naturelles ou simplement altérées voisines (par exemple : sibb proche de la ou de sib), souvent éliminées dans la pratique ou la théorie simplifiée.
La gamme complète de Pythagore présente ainsi deux types de Demi-tons, mais un seul pour chaque catégorie (diatonique et chromatique) :
- Demi-ton diatonique appelé limma, de rapport 256/243, placé soit entre les Notes mi - fa et si - do, soit entre certaines Notes bémolisées et la Note naturelle immédiatement supérieure (dob - do, réb - ré, solb - sol, lab - la).
- Demi-ton chromatique appelé apotome, de rapport 2187/2048, placé entre une Note naturelle et sa forme diésée (par exemple do - do#).
Voir synthèse dans Intervalles ou [HAE Construction].
|
Dans la Gamme de Pythagore, les Intervalles entre Notes Conjointes présentent deux rapports fondamentaux : 9/8 et 256/243 (voir second axe en Figure ci-dessus). Le premier définit le Ton, le second définit le Demi-ton diatonique. - L'alternance des intervalles selon le schéma TTDTTTD (T = ton, D = demi-ton) est une conséquence inévitable du fait que les Notes proviennent d'une chaîne de Quintes justes (rapport 3/2) et qu'on les ramène toutes dans la même Octave (rapport 2/1). - Cette stupéfiante propriété découle d'un principe mathématique (théorème des trois longueurs) appliqué à la musique. Lorsqu'on génère les n premiers multiples d'un rapport musical donné R (par exemple la Quinte juste 3/2) et qu'on ramène chaque fréquence dans une même Octave (c'est-à-dire modulo le rapport 2/1), les points obtenus sur le cercle des fréquences de l'Octave se répartissent en arcs d'au plus trois longueurs différentes (1, 2 ou 3 selon les valeurs de n et de R). Dans le cas particulier où R = 3/2 correspondant à la chaîne des Quintes justes, les tassements de la gamme diatonique (demi-tons) prévus par ce théorème se font en deux endroits précis : entre les Notes fa# - sol (remplacé par mi - fa dans la gamme diatonique pythagoricienne) et si - do. - Cette approche mathématique explique pourquoi il n'y a qu'un Demi-ton entre les Notes mi - fa et si - do. - Ainsi, la construction pythagoricienne, issue du cycle des Quintes (3/2) ramenées dans l'Octave (2/1) et de la Note fa représentative de la Quarte juste (4/3), rejoint la théorie de Zarlino qui fonde la consonance musicale sur la perception privilégiée des trois rapports simples : 2/1, 3/2 et 4/3. - La Quinte du loup reste toutefois un problème. En Gamme Majeure, les musiciens qui accordent leurs Instruments sur la Gamme de Pythagore reportent la Quinte du loup dans un Intervalle peu utilisé, en général sol# - mib, et utilisent alors les Notes suivantes de la Gamme chromatique : mib - sib - fa - do - sol - ré - la - mi - si - fa# - do# - sol#. - Par ailleurs, les Demi-tons (en versions diatonique et chromatique) sont inégaux, ce qui rend la Transposition difficile. - Toutes ces raisons font que la Gamme de Pythagore est peu utilisée par les compositeurs. - Cette Gamme reste néanmoins utile sur les Instruments que l'on accorde par Quintes (violon par exemple) ou par Quartes (contrebasse par exemple). Elle permet également à certains solistes (violoniste, chanteur, etc.) de jouer naturellement une Ligne mélodique plus expressive, la Tierce majeure étant plus haute que dans les autres Gammes usuelles (voir Tableau ci-dessous). |
| Notes | do | ré | mi | fa | sol | la | si | do | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intervalles en Mode Majeur | Ton | Ton | 1/2 Ton | Ton | Ton | Ton | 1/2 Ton | ||||||||
| Gamme de Zarlino | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||
| Gamme de Pythagore | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | ||||||||
| Gamme tempérée | 22/12 | 22/12 | 21/12 | 22/12 | 22/12 | 22/12 | 21/12 |
La Gamme tempérée est la Gamme qui divise l'Octave en Intervalles égaux, sans se préoccuper de la Consonance entre les Notes ainsi déterminées.
Le découpage le plus répandu contient 12 Intervalles (Demi-tons) qui ont chacun une largeur de 1/12 Octave correspondant à un rapport de Fréquences entre deux Notes Conjointes de 1,05946 = 21/12.
Le Tableau ci-dessus compare les trois Gammes diatoniques usuelles (Zarlino, Pythagore et Tempérée), en Mode Majeur, selon leurs Intervalles respectifs donnés par le rapport de Fréquences entre deux Notes Conjointes.
La Gamme tempérée, dont la paternité est généralement attribuée au musicien Andreas Werckmeister en 1691, est largement utilisée en musique occidentale depuis le 18e siècle. J.S. Bach fut l'un des premiers musiciens à l'adopter (cf "Le Clavier bien tempéré", recueil d'oeuvres écrites de 1722 à 1744).
Bien que difficile à accorder et au prix de n'avoir plus aucun Intervalle "juste" au sens de Zarlino ou de Pythagore, elle présente toutefois de nombreux avantages (uniformisation des Demi-tons, Transpositions et Modulations à l'infini, etc.).
La Gamme est tempérée sur la plupart des Instruments à clavier (piano, orgue, clavecin, harmonium, accordéon, etc.), sur certains Instruments à cordes (guitare, mandoline, luth, harpe, viole, etc.) et sur les Instruments à vent avec clés ou pistons (trompette, tuba, clarinette, hautbois, etc.).
En musique, la Consonance est la combinaison de Sons, telle un Intervalle ou un Accord, perçue comme agréable à l'oreille. Dans le cas contraire, on parle de Dissonance.
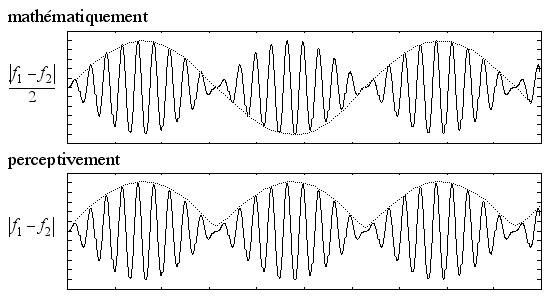
Figure ci-dessus : Battement physique et battement psychoacoustique de deux sons purs de fréquences f1 et f2
Deux Sons purs confondus (de Fréquences identiques ou très proches), ou au contraire séparés de plus d'une Tierce mineure (dont le rapport des Fréquences est supérieur à 6/5), sont perçus comme agréables à l'oreille (Sons Consonants). Dans le cas contraire, les Sons sont Dissonants.
Lorsque deux Sons purs de Fréquences f1 et f2 sont joués simultanément, l'oreille ressent les impressions suivantes (cf [PIER, p.76]) :
- Si f1 et f2 sont identiques ou très proches, les Sons sont confondus.
- Si f1 et f2 sont légèrement éloignés, l'oreille entend, en plus d'une Fréquence voisine de f1 et f2, un Battement lent qui ne nuit pas à l'impression d'Harmonie mais donnent simplement l'impression d'un Tremolo, une augmentation et diminution d'amplitude (voir Figure ci-dessus et Explication du "Battement physique" dans le Lexique).
- Si f1 et f2 sont un peu plus éloignés, l'oreille entend un Battement rapide ou bien une impression désagréable de dureté sans Battement. Dans les deux cas, les Sons sont Dissonants.
- Si la différence entre f1 et f2 dépasse un seuil appelé "largeur de Bande critique", l'impression désagréable disparaît et l'oreille entend des Sons séparés et Consonants.
La largeur de cette Bande critique est de 0,26 Octave (= log2(6/5)) correspondant à l'Intervalle "Tierce mineure" (de rapport 6/5 en Fréquence).
L'oreille décompose les Fréquences comme suit (cf [PIER, p.76]) :
- Les Fréquences situées à l'intérieur d'une même largeur de Bande critique envoient au cerveau un signal mélangé par les mêmes fibres nerveuses.
- Au contraire, les Fréquences séparées de plus d'une largeur de Bande critique envoient des signaux par des fibres nerveuses distinctes.
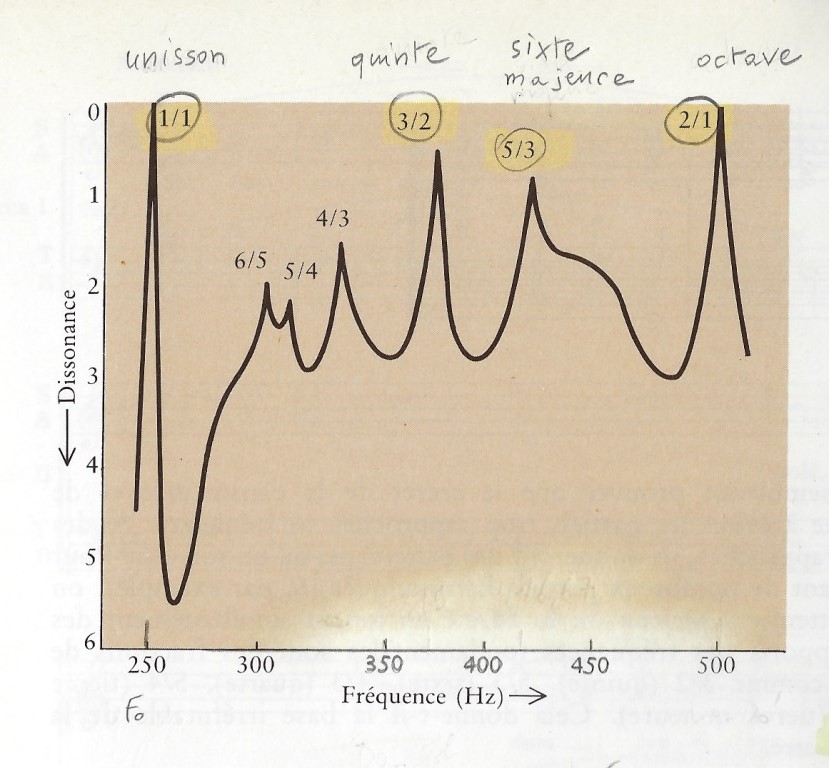

Figure 1 et 2 ci-dessus : Consonance de deux sons musicaux en fonction du rapport de leurs fréquences fondamentales.
Les Sons musicaux ne sont pas des Sons purs mais contiennent, comme les sons du piano, beaucoup d'Harmoniques. Contrairement à une idée reçue, la Consonance entre deux Sons musicaux ne dépend pas du rapport entre leurs Fréquences Fondamentales mais de la concordance entre les séries Harmoniques de chaque Son.
Deux Sons musicaux ayant beaucoup d'Harmoniques confondus (de Fréquences identiques ou très proches), ou au contraire séparés de plus d'une Tierce mineure (dont le rapport des Fréquences est supérieur à 6/5), sont perçus comme agréables à l'oreille (Sons Consonants). Dans le cas contraire, l'oreille perçoit un Battement rapide ou une impression désagréable de dureté sans Battement, et les Sons sont Dissonants (cf [PIER, pp 76 et 79]).
Redoublement (à ne pas confondre avec Doublure) :
Tout Redoublement dans un Intervalle améliore sa Consonance.
Le Tableau suivant donne la liste des Intervalles Consonants avec leurs noms, leurs Notes (en do Majeur) et le rapport idéal des Fréquences selon la Gamme de Zarlino (cf [PIER, p.64]).
| Nom de l'Intervalle | Notes en do Majeur | Rapport des Fréquences selon Gamme de Zarlino |
|---|---|---|
| Unisson | do - do | 1/1 |
| Tierce mineure | mi - sol | 6/5 |
| Tierce majeure | do - mi | 5/4 |
| Quarte juste | do - fa | 4/3 |
| Quinte juste | do - sol | 3/2 |
| Sixte mineure | mi - do | 8/5 |
| Sixte majeure | do - la | 5/3 |
| Octave | do - do à l'Octave | 2/1 |
La Figure 1 ci-dessus (cf [PIER, p.79]) montre la Consonance de deux Sons musicaux en fonction du rapport de leurs Fréquences Fondamentales. Chaque Son musical comporte une Fondamentale (f) et cinq Harmoniques supérieurs (2f, 3f, 4f, 5f, 6f). La Fréquence 250 Hz est notée f0.
Les Intervalles les plus Consonants sont alors : l'Unisson (rapport 1/1), l'Octave (rapport 2/1), la Quinte (rapport 3/2) et la Sixte majeure (rapport 5/3).
Les autres Intervalles en Figure 1 et 2 (la Quarte (rapport 4/3), la Tierce majeure (rapport 5/4)), la Tierce mineure (rapport 6/5)) et la Sixte mineure (rapport 8/5) sont également Consonants mais un peu moins.
A noter que la Consonance de la Quarte juste est qualifiée de "mixte" uniquement dans le contexte d'un Accord. Elle peut rendre l'Accord légèrement Dissonant quand elle est en Basse.
Le mot "Harmonique" est pris ici au sens large (la Fondamentale étant l'Harmonique de rang 1).
On se limite aux six premiers Harmoniques de chaque son, l'intensité des Harmoniques supérieures (7f, 8f, etc.) décroissant rapidement pour la plupart des sons musicaux.
Le Tableau ci-dessous montre la concordance des séries d'Harmoniques entre plusieurs Sons musicaux.
La distance horizontale mesure en Octaves la séparation des Fréquences, c'est-à-dire que les Harmoniques de rapport 2/1 se trouvent à une Octave les unes des autres. La Bande critique de largeur 0,26 Octave (Tierce mineure) correspond à une distance horizontale de 5 cases (ou à un espacement visuel de 4 cases).
La première ligne du Tableau donne le numéro d'Octave.
La seconde ligne donne la position (n) des Harmoniques (nf) du Son grave.
Les lignes suivantes donnent, en regard du Son grave, la position des Harmoniques de plusieurs Sons plus aigus.
| * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | * | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Numéro d'Octave | 0 | 1 | 2 | 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Son grave | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Unisson (1/1) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tierce mineure (6/5) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tierce majeure (5/4) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Quarte juste (4/3) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Quinte juste (3/2) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sixte mineure (8/5) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sixte majeure (5/3) | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Octave (2/1) | 1 | 2 | 3 | 4 | 5 | 6 |
Ce Tableau montre clairement les résultats suivants :
Les Harmoniques de l'Unisson (f, 2f, 3f, 4f, 5f, 6f) et du Son grave sont identiques. Les deux Sons sont donc parfaitement Consonants.
Les Harmoniques de l'Octave sont : 2f, 4f, 6f, 8f, 10f, 12f.
Tous les Harmoniques de l'Octave (2f, 4f et 6f) coincident avec ceux du Son grave. Les deux Sons sont donc parfaitement Consonants.
Les Harmoniques de la Quinte sont : (3/2)f, 3f, (9/2)f, 6f, (15/2)f, 9f.
Deux Harmoniques de la Quinte (3f et 6f) coincident avec ceux du Son grave.
Le premier Harmonique (3/2)f de la Quinte est bien séparé du premier Harmonique f et du second Harmonique 2f du Son grave, par au moins une Tierce mineure.
Le troisième Harmonique (9/2)f de la Quinte tombe entre le cinquième Harmonique 5f (0,15 Octave en dessous) et le quatrième Harmonique 4f (0,17 Octave au-dessus) du Son grave. Ces deux Intervalles sont un peu inférieurs à une Tierce mineure.
Globalement, les deux Sons sont donc Consonants (sans être toutefois parfaitement Consonants comme l'Unisson ou l'Octave).
Les Harmoniques de la Sixte majeure sont : (5/3)f, (10/3)f, 5f, (20/3)f, (25/3)f, 10f.
Un seul Harmonique de la Sixte majeure (5f) coincide avec celui du Son grave.
Le premier Harmonique (5/3)f de la Sixte majeure est bien séparé du premier Harmonique f et du second Harmonique 2f du Son grave.
Le deuxième Harmonique (10/3)f de la Sixte majeure tombe au-dessus du troisième Harmonique 3f du Son grave (0,15 Octave au-dessus). Cet Intervalle est un peu inférieur à une Tierce mineure.
Le quatrième Harmonique (20/3)f de la Sixte majeure tombe au-dessus du sixième Harmonique 6f du Son grave (0,15 Octave au-dessus). Cet Intervalle est un peu inférieur à une Tierce mineure.
Globalement, les deux Sons sont donc Consonants (sans être toutefois parfaitement Consonants comme l'Unisson ou l'Octave).
Les accordeurs de piano ont une méthode systématique pour Accorder un piano, basée sur les Battements issus de la non-concordance de certaines séries d'Harmoniques entre Notes.


Figure 1 ci-dessus : Une Cadence qui va de l'accord de Septième de Dominante, dissonant, à l'accord de Tonique, consonant.
Figure 2 ci-dessus : Accords parfaits majeur et mineur, suivis chacun de leurs deux Renversements.
Lorsqu'on joue ensemble plus de deux Notes, la Consonance suit la règle Psychoacoustique concernant la Consonance entre deux sons musicaux.
Le secret de la Consonance consiste à éviter les Harmoniques trop rapprochés en Fréquence. Par exemple, dans un Accord de Septième de Dominante ou dans un Accord de Tonique (voir Figure ci-dessus), si on enlève soigneusement (par ordinateur) tous les Harmoniques se trouvant à moins d'une Tierce mineure, le premier Accord (qui est Dissonant) devient Consonant et le second Accord devient plus Consonant qu'il ne l'est naturellement (cf [PIER, p.80]).
A noter également que le groupement de trois Notes formant entre elles des Intervalles Consonants contribue, certes, à rendre l'Accord Consonant mais ne le garantit pas toujours. Par exemple, la Quarte juste peut rendre l'Accord légèrement Dissonant quand elle est en Basse de l'Accord.
Redoublement (à ne pas confondre avec Doublure) :
Tout Redoublement dans un Accord améliore sa Consonance.
Les Accords de trois notes habituellement considérés comme les seuls Consonants sont les quatre Accords suivants, déjà utilisés au 16e siècle :
1- L'Accord parfait majeur, par exemple : do - mi - sol (voir Accord n°1 en Figure 2 ci-dessus), qui est l'empilement d'une Tierce majeure (do - mi) et d'une Tierce mineure (mi - sol).
2- L'Accord parfait mineur, par exemple : do - mib - sol (voir Accord n°4 en Figure 2 ci-dessus), qui est l'empilement d'une Tierce mineure (do - mib) et d'une Tierce majeure (mib - sol).
3- L'Accord de sixte majeure, par exemple : mib - sol - do (voir Accord n°5 en Figure 2 ci-dessus, 1er Renversement de l'Accord parfait mineur), qui est l'empilement d'une Tierce majeure (mib - sol) et d'une Quarte juste (sol - do).
4- L'Accord de sixte mineure, par exemple : mi - sol - do (voir Accord n°2 en Figure 2 ci-dessus, 1er Renversement de l'Accord parfait majeur), qui est l'empilement d'une Tierce mineure (mi - sol) et d'une Quarte juste (sol - do).
On en déduit la forme Fondamentale des Accords en Musique Tonale, qui est celle qui empile des Intervalles de Tierce (mineure ou majeure), et ceci quel que soit le nombre de Notes composant l'Accord.
D'où finalement les trois grandes classes d'Accords :
- La classe des Accords de trois notes (ou Accords de Quinte), dont les Notes constitutives sont la Fondamentale, la Tierce (mineure ou majeure) et la Quinte (juste, diminuée ou augmentée).
- La classe des Accords de quatre notes (ou Accords de Septième), dont les Notes constitutives sont celles d'un Accord de trois notes, plus une Septième (majeure, mineure ou diminuée).
- La classe des Accords de cinq notes (ou Accords de Neuvième), dont les Notes constitutives sont celles d'un Accord de quatre notes, plus une Neuvième (majeure, mineure ou augmentée).
(cf [PIER, pp 79 et 173])
Si un Son musical comporte plus de six Harmoniques (f, 2f, 3f, 4f, 5f, 6f, etc.), les Harmoniques les plus aigus se trouveront toujours à moins d'une Tierce mineure l'un de l'autre (voir Son grave dans le second Tableau ci-dessus) et le Son donnera une impression de Dissonance interne. C'est le cas du clavecin, riche en Harmoniques, ou dans certains sons électroniques avec ondes rectangulaires ou en dents de scie.
Naturellement, si les Notes prises individuellement sont déjà Dissonantes, elles le seront encore plus si elles sont jouées en Accord avec d'autres.
Au piano, les marteaux sont placés pour frapper la corde à un septième de sa longueur de sorte qu'ils ne peuvent pas faire vibrer la corde à la Fréquence du septième Harmonique, ce qui élimine quasi-totalement toute Dissonance interne.

Figure ci-dessus : L'Accord n°1 est un Accord parfait majeur.
L'Accord parfait majeur est l'ensemble des trois Notes suivantes jouées ensemble : une Note de Fréquence Fondamentale f, la Tierce majeure supérieure de Fréquence Fondamentale 5/4 f et la Quinte juste supérieure de Fréquence Fondamentale 3/2 f, par exemple : do - mi - sol.
Cet Accord est remarquable car il cumule à lui seul trois propriétés Psychoacoustiques différentes.
Le mot "Harmonique" est pris ici au sens large (la Fondamentale étant l'Harmonique de rang 1).
1) Cet Accord est présent à l'état pur au sein de chaque Note de musique.
Tout Son périodique possède un Accord parfait majeur situé deux Octaves plus haut que sa Fondamentale, dans ses Harmoniques de rangs 4, 5 et 6. On peut en effet constater que :
- la division du rang 5 par le rang 4, soit le rapport 5/4, est la Tierce majeure.
- la division du rang 6 par le rang 4, soit le rapport 3/2, est la Quinte juste.
Par ailleurs, cet Accord se trouve renforcé en intensité par les trois premiers Harmoniques. On peut en effet constater que :
- les rangs 1 et 2 "répètent" la même Note que la Note la plus grave de l'Accord (rang 4).
- le rang 3 "répète" la même Note que la Note la plus aigüe de l'Accord (rang 6).
Au total, une oreille exercée peut entendre cet Accord dans chaque Note de musique jouée isolément.
2) Cet Accord est considéré comme l'Accord le plus Consonant.
Si f est, par exemple, la Fréquence Fondamentale du do, il s'ensuit que :
- les Harmoniques du do sont : f, 2f, 3f, 4f, 5f, 6f.
- les Harmoniques du mi sont : (5/4)f, (5/2)f, (15/4)f, 5f, (25/4)f, (15/2)f.
- les Harmoniques du sol sont : (3/2)f, 3f, (9/2)f, 6f, (15/2)f, 9f.
Par une analyse analogue à celle faite pour la Consonance entre deux sons musicaux, on montre qu'il existe une quasi-parfaite concordance entre les séries Harmoniques de chacun des trois Sons composant l'Accord.
3) Cet Accord donne une impression d'harmonie (cf [PIER, p.90]).
Tous les Harmoniques de cet Accord sont des multiples entiers de la Fréquence fb = (1/4) f : multiples de 4 pour le do, multiples de 5 pour le mi et multiples de 6 pour le sol.
En écoutant cet Accord, l'oreille exercée perçoit une Hauteur de deux Octaves plus bas que le do, correspondant à la Fréquence fb. D'où l'impression d'une certaine Harmonie.
Rameau a considéré cet Accord comme la base de l'Harmonie musicale. Mais l'Harmonie ne se résume pas aux Accords parfaits majeurs.
Pour la plupart des musiciens, l'Harmonie est la combinaison Dissonante de Notes, pleines de tensions, qui se résolvent miraculeusement en un Accord Consonant.
Pour le compositeur américain Lejaren Hiller, "la musique est un compromis entre la monotonie et le chaos".
Pour l'Auteur, l'harmonie serait l'alternance entre deux intérêts (ou plaisirs) à la fois complémentaires et antagonistes :
- d'une part, la perception d'Intervalles et d'Accords déjà présents à l'état pur dans les six premiers Harmoniques de chaque Son musical (essentiellement l'Octave, la Quinte, la Quarte, la Sixte majeure et l'Accord parfait majeur), donnant une impression de satisfaction, voire d'attente comblée,
- d'autre part, la perception de motifs sonores autres, donnant un sentiment de nouveauté, voire d'imprévu, par rapport aux motifs habituels.
Cette alternance entre habitude et nouveauté, tout en évitant soigneusement la saturation donnant un sentiment de monotonie, voire de lassitude, dépendrait largement des origines culturelles du compositeur et de l'éducation de son oreille musicale.
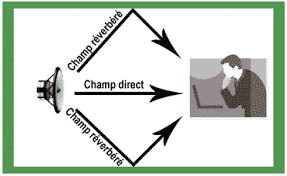
Figure ci-dessus : Réverbération en milieu clos.
En milieu clos, le Son direct n'est perceptible qu'à courte distance de la source (voir Figure ci-dessus) car son énergie décroit avec la distance d comme 1/d2.
En conséquence, assez loin de la source (dans une salle de spectacle notamment), les Sons réfléchis par les parois de la salle constituent l'essentiel du Son perçu (cf [MAT Introduction]).
Les conditions d'une bonne acoustique interne sont alors données par le Temps de réverbération (Tr) de la salle.
Ce temps ne doit pas être trop petit, auquel cas le Son direct serait insuffisamment prolongé par les Sons réfléchis (comme pour un local trop bien isolé type "chambre sourde").
Ce temps ne doit pas être non plus trop grand, auquel cas le même Son serait entendu plusieurs fois (phénomème d'écho qui se produit quand l'intervalle de temps séparant les arrivées successives des ondes est supérieur à 0,1 s) ou bien des Sons émis successivement se trouveraient fusionnés avant leur extinction et rendraient la compréhension inintelligible (parole ou musique).
Le Temps de réverbération optimal (Tr opt) est donc un compromis entre une sonorité insuffisante et une sonorité excessive du local.
Ce Temps doit être d'environ 0,5 s pour des pièces d'habitation et de 1 s pour des salles de spectacle de 500 m3. Plus précisément, en fonction du volume V du local, le Temps (Tr opt) est le suivant (selon formule de Stephen et Bate) :
Tr opt = a (0,0118 V1/3 + 0,1070)
où a est une constante qui vaut 4 pour le Langage parlé, 4,5 pour l'opéra, 5 pour les orchestres et 6 pour les choeurs.
Dans un projet de construction de salle, pour obtenir ce Temps optimal qui est toujours plus petit que celui de la salle nue, il faut employer des matériaux absorbant le Son.
La formule du Temps de réverbération (Tr) permet de faire ces choix selon la catégorie des matériaux absorbants (voir [PUJ Projet]) :
- matériaux poreux absorbant surtout les Sons de Fréquence aigüe ;
- matériaux à base de Membrane vibrante absorbant les basses ;
- matériaux constitués de Résonateurs absorbant généralement les médiums.
Pour les grandes salles (plus de 1000 m3), il convient de compléter cette approche statistique par une étude géométrique visant à donner aux parois de la salle une forme déviant les rayons réfléchis acoustiquement dangereux (voir [MAT Introduction][PUJ Projet]).
Pour les petites salles type auditorium par exemple (moins de 150 m3), il convient de compléter cette approche statistique par une étude ondulatoire visant à prendre en compte l'impédance mécanique des parois génératrice de Fréquences propres (voir [MAT Introduction][PUJ Projet]).
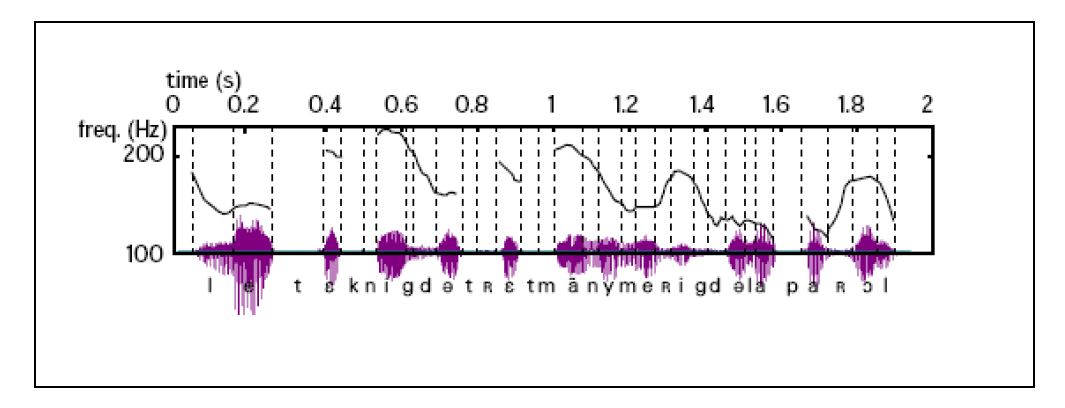
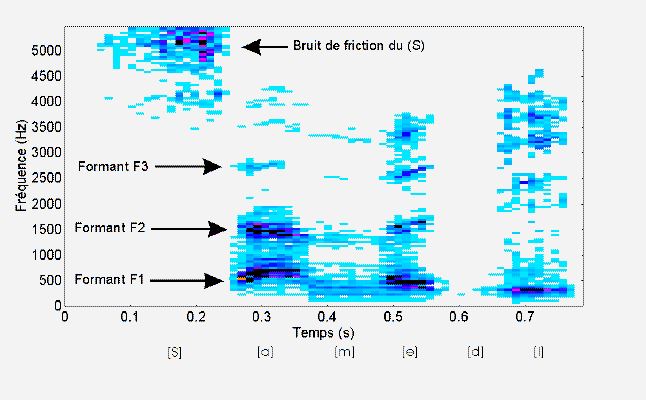
Figure 1 ci-dessus : Evolution temporelle de la Fréquence Fondamentale F0 dans la phrase "Les techniques de traitement numérique de la parole" (cf Synthèse polyphonique de l'arabe standard, Touahri Dalida, Blida, 2008 en référence à [DUTO]).
Figure 2 ci-dessus : Evolution temporelle des Formants F1, F2 et F3 dans la phrase "Samedi" (cf Le blog de outilsrecherche, Notes 3.1.1 - Décodage du Signal de la Parole).
Le langage parlé est un langage basé sur l'articulation de Sons particuliers appelés Syllabes. Le langage parlé est caractérisé acoustiquement par les paramètres suivants :
1- La Fréquence Fondamentale F0 produite par le larynx (cordes vocales), laquelle permet de faire la différence entre la Voix d'un homme (100 à 150 Hz), d'une femme (200 Hz à 300 Hz) ou d'un enfant (350 à 400 Hz). cf [CAIL].
La Figure 1 ci-dessus montre en exemple l'évolution temporelle de F0 dans la Phrase "Les techniques de traitement numérique de la parole".
On constate que, à l'intérieur des zones voisées, F0 subit peu de variations dans le temps. F0 ne peut donc pas caractériser un Phonème (Voyelle ou Consonne).
2- Les quatre premiers Formants produits par les Résonateurs naturels du Conduit vocal (cf [PHON]) :
- le Formant F1 produit par le pharynx dans le Registre 300 à 800 Hz,
- le Formant F2 produit par la cavité buccale dans le Registre 800 à 2500 Hz,
- le Formant F3 produit par la cavité labio-dentale dans le Registre 2000 à 3000 Hz,
- le Formant F4 (appelé "singing Formant") produit par la position du voile du palais (autorisant ou non le passage de l'air dans les fosses nasales) autour de 2800 Hz chez l'homme et de 3200 Hz chez la femme.
Les Formants F1, F2 et F3 donnent le Timbre de la Voyelle et participent à celui des Consonnes dans la mesure où ils marquent en même temps les Transitions entre Voyelles.
La Figure 2 ci-dessus montre en exemple l'évolution temporelle des Formants F1, F2 et F3 dans la Phrase "Samedi". On distingue clairement les Formants des trois Voyelles "a", "e" et "i", ainsi que le Bruit de friction de la Consonne fricative "S".
Le Formant F4 participe à la coloration du Timbre propre à chaque locuteur.
3- Le Voisement qui s'ajoute à l'articulation lorsque les cordes vocales vibrent.
4- La Prosodie (ou "musique de la parole") qui permet de transmettre des émotions tout comme la musique instrumentale.
Le langage parlé peut se formaliser comme suit :
- Le Langage parlé est une succession de Phrases.
- Une Phrase est une succession de couples Mot-Silence, le Silence n'étant pas souvent fortement marqué à l'oral.
- Un Mot est une succession ininterrompue de Sons séparés par une frontière inter-sons (laquelle n'est pas un Silence). Le Mot "opérateur" par exemple comprend quatre Sons distincts (o.pé.ra.teur).
- Un Son (ou Syllabe) est une concaténation de Phonèmes (Voyelles et/ou Consonnes) prononcée en une seule émission de voix. En français, le noyau d'une Syllabe est toujours un Phonème de type voyelle (V), entouré éventuellement de un ou plusieurs autres Phonèmes de type consonne (C). Par exemple, le Mot monosyllabique "film" est une simple Syllabe du type CVCC comprenant quatre Phonèmes distincts (/f/ /i/ /l/ /m/).
- Un Phonème est la plus petite unité que l'on puisse isoler par segmentation dans la chaîne parlée. Les Voyelles sont caractérisées par le libre passage de l'air dans le Conduit vocal. Les Consonnes, au contraire, sont caractérisées par l'obstruction momentanée (complète ou partielle) du passage de l'air. Les Phonèmes se caractérisent essentiellement par des Formants, des Transitions de Formants et des Bruits d'explosion ou de friction, visualisables sur des enregistrements de type Sonagramme.
Le Lexique ci-dessous détaille les termes utilisés dans cette page, listés par ordre alphabétique.
En Langage parlé, l'Accent est un des composants de la Prosodie qui traduit le relief sonore donné à certaines Syllabes dans la chaîne parlée.
On distingue deux types d'Accent :
L'Accent tonique, inhérent à la langue, délimite des unités de sens dans la Phrase (groupe nominal, groupe verbal, complément de lieu, de temps, etc.) en augmentant l'Intensité, la Durée et/ou la Hauteur de certaines Syllabes.
En français, l'Accent tonique est principalement déterminé par l'Intensité et la Durée. Il est toujours placé sur la dernière Syllabe prononcée de chaque groupe de Mots. Cette Syllabe sera plus intense et plus longue que les autres. Exemple : "la bouteille de vin est terminée."
L'Accent expressif (ou Accent d'insistance), facultatif, est employé pour mettre un élément en évidence.
Le terme "Accentuation" est utilisé différemment selon le contexte musical :
- Accentuation en terme de Durée : voir Figure de Note.
- Accentuation en terme d'Intensité sonore : voir Nuance.
- Accentuation en terme de Temps : voir Mesure.
Voir Portée.


Définition :
L'Antiquité et le Moyen Age se contentait d'une seule Voix et appelait "Accord" un Intervalle harmonique de deux Sons, Redoublés ou non.
Vers la fin du Moyen Age naquit le Contrepoint pour lequel un "Accord" n'est que le résultat fortuit de la simultanéité d'Intervalles harmoniques produite par la superposition organisée de Lignes mélodiques distinctes.
A la Renaissance s'est progressivement mise en place la Musique Tonale pour laquelle un Accord est l'ensemble d'au moins trois Notes jouées ensemble ou quasiment ensemble (Accord arpégé), les Noms des Notes étant généralement différents (l'Accord do - mi - do à l'Octave restant par exemple un Accord incomplet).
Un Accord est donc une combinaison de plusieurs Intervalles, généralement Consonants (voir Figure 2 ci-dessus).
Trois grandes classes ou familles d'Accords existent :
- La classe des Accords de trois notes (ou Accords de Quinte),
- La classe des Accords de quatre notes (ou Accords de Septième),
- La classe des Accords de cinq notes (ou Accords de Neuvième).
Notation et nommage :
En notation musicale, lorsque les Notes sont simultanées et de même Durée, elles sont reliées par une hampe verticale, sauf les Rondes (voir Figure 2 ci-dessus).
L'Accord porte le Nom de sa Fondamentale (exemple : Accord de do Majeur). Les autres Notes constitutives portent le nom de l'Intervalle ascendant qui sépare cette Note de la Fondamentale, et ceci même si la Fondamentale ne se trouve pas à la Basse.
Attention : ce nommage est différent du Chiffrage de l'Accord qui se fait par rapport à la Basse et non pas par rapport à la Fondamentale. Il est donc prudent, lorsqu'on parle par exemple d'une "Tierce", de préciser s'il s'agit de la Tierce "de l'Accord" - autrement dit, la Tierce de la Fondamentale - ou bien s'il s'agit de la Tierce "de la Basse" représentée par le Chiffrage, ceci afin d'éviter tout malentendu en cas d'Accord Renversé.
Etat fondamental :
Un Accord est dit "à l'état fondamental" lorsque sa Basse est la Fondamentale de l'Accord (voir les deux premiers Accords de la Figure 1 ci-dessus, la Fondamentale étant indiquée en couleur rouge). Il n'est pas forcément formé d'un empilement de Tierces comme le 1er Accord do - mi - sol de la Figure. La Position des Notes peut être différente : par exemple, le 2ème Accord do - sol - mi de la Figure est aussi un Accord à l'état fondamental.
L'Accord est dit "Renversé" dans le cas contraire (état "non-fondamental").
Attention : selon le contexte, la terminologie "état fondamental" signifie souvent "état fondamental réduit" (voir ci-après).
Etat fondamental réduit :
Un Accord est dit "classé ou à l'état fondamental réduit" lorsqu'il est normalisé par réduction à un empilement de Tierces (voir le 1er Accord de la Figure 1 ci-dessus). Cette réduction s'obtient en abaissant les Notes supérieures d'une Octave jusqu'à obtenir un empilement de Tierces (exemples : do - mi - sol ; do - mib - sol ; do - mi - sol - sib - ré).
Sur la Figure 1 ci-dessus, les trois derniers Accords (do - sol - mi, mi - sol - do, et sol - do - mi) ont pour Accord à l'état fondamental réduit le 1er Accord do - mi - sol, dont la Fondamentale est do, la Tierce est mi et la Quinte est sol.
Chiffrage et Fonction tonale :
Les Accords sont Chiffrés pour des besoins de description et d'analyse tonale de ces Accords. Deux Chiffrages existent : le Chiffrage classique (appelé "basse continue") et le Chiffrage moderne (en musique Jazz/Rock).
Les Accords s'utilisent comme Fonction dans leur contexte tonal.
Disposition et enchaînement :
Dans un morceau musical, on distingue, d'une part la Disposition verticale des Accords (i.e. les Accords au repos), d'autre part l'Enchaînement des Accords (i.e. les Accords en Mouvement), lesquels se font selon des règles Harmoniques.

La classe des Accords de cinq notes (ou Accords de Neuvième) regroupe les Accords dont les Notes constitutives sont celles d'un Accord de quatre notes, plus une Neuvième (majeure, mineure ou augmentée).
D'où les dix espèces d'Accord :
1. Accord de Neuvième majeure de Dominante, ou Accord de Neuvième majeure, Septième mineure et Parfait majeur (exemple : ré - fa# - la - do - mi)
2. Accord de Neuvième mineure de Dominante, ou Accord de Neuvième mineure, Septième mineure et Parfait majeur (exemple : ré - fa# - la - do - mib)
3. Accord de Neuvième majeure et Septième mineure (exemple : ré - fa - la - do - mi)
4. Accord de Neuvième mineure et Septième mineure (exemple : ré - fa - la - do - mib)
5. Accord de Neuvième mineure et Quinte diminuée (exemple : ré - fa - lab - do - mib)
6. Accord de Neuvième majeure et Septième majeure (exemple : ré - fa# - la - do# - mi)
7. Accord de Neuvième augmentée (exemple : ré - fa# - la - do# - mi#)
8. Accord de Neuvième mineure et Septième diminuée (exemple : ré - fa - lab - dob - mib)
9. Accord de Neuvième majeure, Septième majeure et Parfait mineur (exemple : ré - fa - la - do# - mi)
10. Accord de Neuvième majeure et Quinte augmentée (exemple : ré - fa# - la# - do# - mi)
La Figure ci-dessus montre en exemple l'ensemble des Accords de cinq notes porté par les différents Degrés de la Gamme de do majeur et de la Gamme de do mineur harmonique.
Le Tableau ci-dessous (cf [Gui]) donne la Structure des Accords de cinq notes portés par les différents Degrés pour le Mode Majeur et les Modes Mineurs.
Légende du Tableau :
Neuvième : M = Majeur, m = mineur, aug9 = augmentée
Septième : M = Majeur, m = mineur, dim7 = diminuée
Quinte : dim = diminué, aug = augmenté
Accord Parfait de trois notes : PM = Parfait Majeur, Pm = Parfait mineur
| Degrés portant les Accords de cinq notes | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| Mode Majeur | M M | M m | m m | M M | M m PM | M m | m m dim |
| Mode Mineur harmonique ou classique | M M Pm | m m dim | M M aug | M m | m m PM | aug9 | m dim7 |
| Mode Mineur mélodique ascendant | M M Pm | m m | M M aug | M m PM | M m PM | M m dim | m m dim |
| Mode Mineur naturel ou mélodique descendant | M M | m m dim | M M | M m | m m | M M | M m PM |

Un Accord de quarte et sixte est le deuxième Renversement d'un Accord de trois notes, Parfait ou non (voir exemple en Figure ci-dessus, la Fondamentale étant indiquée en couleur rouge).
Il se compose d'une Basse (la Quinte de la Fondamentale), d'une Quarte (la Fondamentale) et d'une Sixte (la Tierce de la Fondamentale).
Lorsque la Quarte est juste, l'Accord est dit Normal et est considéré comme Dissonant. Il peut être soit Majeur (exemple : sol - do - mi) soit Mineur (exemple : sol - do - mib) selon que sa Sixte est majeure ou mineure. On le Chiffre 6/4, mais non pas 6, qui est réservé à l'Accord de sixte.
Lorsque la Quarte est augmentée (exemple : sol - do# - mib), l'Accord est dit Déformé et prend le nom d'Accord de quarte augmentée et sixte.

La classe des Accords de quatre notes (ou Accords de Septième) regroupe les Accords dont les Notes constitutives sont celles d'un Accord de trois notes, plus une Septième (majeure, mineure ou diminuée).
D'où les sept espèces d'Accord :
1. Accord de Septième de Dominante, ou de Septième mineure et Parfait majeur (exemple : mi - sol# - si - ré)
2. Accord de Septième mineure (exemple : mi - sol - si - ré)
3. Accord de Septième mineure et Quinte diminuée (exemple : mi - sol - sib - ré)
4. Accord de Septième majeure (exemple : mi - sol# - si - ré#)
5. Accord de Septième diminuée (exemple : mi - sol - sib - réb)
6. Accord de Septième majeure et Parfait mineur (exemple : mi - sol - si - ré#)
7. Accord de Septième majeure et Quinte augmentée (exemple : mi - sol# - si# - ré#)
La Figure ci-dessus montre en exemple l'ensemble des Accords de quatre notes porté par les différents Degrés de la Gamme de do majeur et de la Gamme de do mineur harmonique.
Le Tableau ci-dessous (cf [Gui]) donne la Structure des Accords de quatre notes portés par les différents Degrés pour le Mode Majeur et les Modes Mineurs.
Légende du Tableau :
Septième : M = Majeur, m = mineur, dim7 = diminué
Quinte : dim = diminué, aug = augmenté
Accord Parfait de trois notes : PM = Parfait Majeur, Pm = Parfait mineur
| Degrés portant les Accords de quatre notes | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| Mode Majeur | M | m | m | M | m PM | m | dim |
| Mode Mineur harmonique ou classique | M Pm | dim | aug | m | m PM | M | dim7 |
| Mode Mineur mélodique ascendant | M Pm | m | aug | m PM | m PM | dim | dim |
| Mode Mineur naturel ou mélodique descendant | m | dim | M | m | m | M | m PM |
Voir Accord de sixte.
Voir Modulation.

La classe des Accords de trois notes (ou Accords de Quinte) regroupe les Accords dont les Notes constitutives sont la Fondamentale, la Tierce (mineure ou majeure) et la Quinte (juste, diminuée ou augmentée).
D'où les quatre espèces d'Accord :
1. Accord parfait majeur (exemple : do - mi - sol)
2. Accord parfait mineur (exemple : do - mib - sol)
3. Accord de quinte diminuée ou plus simplement Accord diminué (exemple : do - mib - solb)
4. Accord de quinte augmentée ou plus simplement Accord augmenté (exemple : do - mi - sol#)
La Figure ci-dessus montre en exemple l'ensemble des Accords de trois notes porté par les différents Degrés de la Gamme de do majeur et de la Gamme de do mineur harmonique.
Le Tableau ci-dessous (cf [Gui]) donne la Structure des Accords de trois notes portés par les différents Degrés pour le Mode Majeur et les Modes Mineurs.
Légende du Tableau :
Tierce : M = Majeur, m = mineur
Quinte : dim = diminué, aug = augmenté
| Degrés portant les Accords de trois notes | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| Mode Majeur | M | m | m | M | M | m | dim |
| Mode Mineur harmonique ou classique | m | dim | aug | m | M | M | dim |
| Mode Mineur mélodique ascendant | m | m | aug | M | M | dim | dim |
| Mode Mineur naturel ou mélodique descendant | m | dim | M | m | m | M | M |

Un Accord de sixte (ou Accord de tierce et sixte) est le premier Renversement d'un Accord de trois notes, Parfait ou non (voir exemple en Figure ci-dessus, la Fondamentale étant indiquée en couleur rouge).
Il se compose d'une Basse (la Tierce de la Fondamentale), d'une Tierce (la Quinte de la Fondamentale) et d'une Sixte (la Fondamentale).
Lorsque l'Accord contient une Quarte juste, l'Accord est dit Normal. Il peut être soit Majeur (exemple : do - mi - la) soit Mineur (exemple : do - mib - lab) selon que sa Tierce est majeure ou mineure. On le Chiffre 6/3 ou plus simplement 6.
Lorsque la Quarte est augmentée (exemple : do - mi - la#) ou diminuée (exemple : do - mi - lab), l'Accord est dit Déformé et prend le nom d'Accord de sixte augmentée ou diminuée.
En Musique tonale, un Accord parfait est l'ensemble des trois Notes suivantes jouées ensemble : une Note de Fréquence Fondamentale f, la Tierce (majeure ou mineure) supérieure et la Quinte juste supérieure, par exemple : do - mi - sol ou do - mib - sol.












Un Accord parfait majeur est un Accord parfait dont la Tierce constitutive est majeure, par exemple : do - mi - sol (voir Accord n°1 en Figure 1 ci-dessus).
Il existe au total 12 Accords parfaits majeurs (voir Figure 2 ci-dessus, cf [FAB Unité 6]). Seuls trois Accords sont sans Altérations : do - mi - sol, fa - la - do, sol - si - ré
Cet Accord est remarquable car il cumule à lui seul trois propriétés Psychoacoustiques différentes.
Le mot "Harmonique" est pris ici au sens large (la Fondamentale étant l'Harmonique de rang 1).
1) Cet Accord est présent à l'état pur au sein de chaque Note de musique.
Tout Son périodique possède un Accord parfait majeur situé deux Octaves plus haut que sa Fondamentale, dans ses Harmoniques de rangs 4, 5 et 6. On peut en effet constater que :
- la division du rang 5 par le rang 4, soit le rapport 5/4, est la Tierce majeure.
- la division du rang 6 par le rang 4, soit le rapport 3/2, est la Quinte juste.
Par ailleurs, cet Accord se trouve renforcé en intensité par les trois premiers Harmoniques. On peut en effet constater que :
- les rangs 1 et 2 "répètent" la même Note que la Note la plus grave de l'Accord (rang 4).
- le rang 3 "répète" la même Note que la Note la plus aigüe de l'Accord (rang 6).
Au total, une oreille exercée peut entendre cet Accord dans chaque Note de musique jouée isolément.
2) Cet Accord est considéré comme l'Accord le plus Consonant.
Si f est, par exemple, la Fréquence Fondamentale du do, il s'ensuit que :
- les Harmoniques du do sont : f, 2f, 3f, 4f, 5f, 6f.
- les Harmoniques du mi sont : (5/4)f, (5/2)f, (15/4)f, 5f, (25/4)f, (15/2)f.
- les Harmoniques du sol sont : (3/2)f, 3f, (9/2)f, 6f, (15/2)f, 9f.
Par une analyse analogue à celle faite pour la Consonance de deux sons musicaux, on montre qu'il existe une quasi-parfaite concordance entre les séries Harmoniques de chacun des trois Sons composant l'Accord.
3) Cet Accord donne une impression d'harmonie (cf [PIER, p.90]).
Tous les Harmoniques de cet Accord sont des multiples entiers de la Fréquence fb = (1/4) f : multiples de 4 pour le do, multiples de 5 pour le mi et multiples de 6 pour le sol.
En écoutant cet Accord, l'oreille exercée perçoit une Hauteur de deux Octaves plus bas que le do, correspondant à la Fréquence fb. D'où l'impression d'une certaine Harmonie.
Rameau a considéré cet Accord comme la base de l'Harmonie musicale. Mais l'Harmonie ne se résume pas aux Accords parfaits majeurs.

| Do | Do# | Ré | Ré# ou Mib | Mi | Fa | Fa# | Sol | Sol# | La | Sib | Si | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 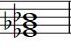 |
 |
 |
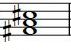 |
 |
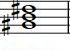 |
 |
 |
 |
Un Accord parfait mineur est un Accord parfait dont la Tierce constitutive est mineure, par exemple : do - mib - sol (voir Accord n°4 en Figure 1 ci-dessus).
Il existe au total 12 Accords parfaits mineurs (voir Figure 2 ci-dessus, cf [FAB Unité 6]). Seuls trois Accords sont sans Altérations : ré - fa - la, mi - sol - si, la - do - mi
Instruments de musique à cordes :
Tous les Instruments de musique à Cordes vibrantes s'accordent en ajustant la tension T des cordes. Ainsi, les 250 cordes d'un piano sont tendues avec une force de 800 N, de sorte que la tension totale qui tend à rapprocher les bords opposés de la table d'harmonie est de 20 tonnes.
La masse des cordes n'est pas par contre ajustable :
- Sur un piano, les cordes graves sont "filées" (i.e. enroulées d'un fil pesant) pour augmenter la masse et elles sont plus longues que les cordes aigües. Par ailleurs, les cordes massives donnent un Son puissant. Pour donner le même volume sonore aux Notes plus aigües, on utilise deux cordes par Note (elles aussi "filées) dans le Registre medium et trois cordes pour le Registre supérieur (cf [PIER p.33]).
- Sur une guitare, les trois ou quatre cordes les plus graves sont également "filées".
Accordage du piano (cf [PIER, pp 76 et 62 à 65]) :
Une Quinte a un rapport de Fréquence de 3/2. Ainsi, le second Harmonique du sol a la même Fréquence 3f que le troisième Harmonique du do de Fréquence Fondamentale f.
Si do et sol sont un peu désaccordés, ces Harmoniques produiront un Battement audible quand les deux Notes seront jouées ensemble.
En accordant le sol pour faire disparaître le Battement avec le do, on s'assure que la Fréquence Fondamentale du sol est exactement 3/2 de celle du do, soit une Quinte parfaite. Les autres Notes peuvent être, elles aussi, accordées de cette façon.
Autre rapport intéressant : une Quarte a un rapport de Fréquence de 4/3. Ainsi, le troisième Harmonique du fa devrait avoir la même Fréquence 4f que le quatrième Harmonique du do (qui est le do situé deux Octaves au-dessus du premier do).
Les accordeurs de piano ont une méthode systématique :
- Ils accordent d'abord les Intervalles à l'intérieur d'une même Octave pour obtenir un nombre fixé de Battements par seconde conduisant à la Gamme tempérée.
- Une fois que ces douze Notes sont accordées, ils accordent ensuite toutes les autres par la méthode des Octaves, sans Battements. Toute Note du piano prise isolément a en effet son second Harmonique 2f situé une Octave plus haute que le son Fondamental f de la Note. Pour chaque Octave, ils écoutent alors les Battements entre le second Harmonique de la Note du bas et la Fondamentale de la Note du haut. Quand le Battement disparaît, l'Octave est juste.
A noter que les pianos sont souvent accordés avec des Octaves élargies, parfois en raison de la raideur des cordes qui s'ajoute à l'effet de tension, parfois parce que le pianiste préfère le Timbre plus Brillant qui en résulte.
Instruments de musique à vent :
Tous les Instruments de musique à vent s'accordent en ajustant la longueur L des Tuyaux sonores. Pour les tuyaux à biseau ou anche, on glisse plus ou moins l'embouchure ou la rasette dans le noyau du tuyau. Pour les tuyaux à bouche, on ferme plus ou moins l'extrémité du tuyau (via l'accordoir si tuyau ouvert ou via le tampon si tuyau fermé).
Les tuyaux d'orgue sont regroupés en rangées de tuyaux, appelées jeux. Un jeu contient un tuyau pour chaque touche du clavier et peut être caractérisé par la longueur de son tuyau le plus long. Les tuyaux appartenant à des jeux différents ont également des formes et des compositions différentes, ce qui leur confèrent des Timbres différents (cf [PIER, p.33]).
Instruments de musique à membrane vibrante :
Tous les Instruments de musique à Membrane vibrante s'accordent en ajustant la tension de la Membrane. Par exemple :
- Pour la caisse claire ou la grosse caisse, deux peaux recouvrant un fût sont tendues par deux cercles reliés par des vis. On ajuste le tension des peaux en tournant plus ou moins les vis.
- Pour les toms, on augmente la raideur de la Membrane en ajoutant une bague en polyester sur sa partie extérieure.
- Pour les percussions indiennes ("tablas" dans le nord de l'Inde et "mridangs" dans le sud de l'Inde), la Membrane en peau d'animal est tendue grâce à une corde qui fait des allers-retours entre le haut et le fond de l'Instrument. On modifie la tension en bougeant des petits cylindres en bois intercalés entre la corde et l'Instrument.


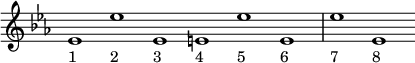

L'Altération est la modification de la Hauteur d'une Note.
Le Dièse (symbole = #) élève la Hauteur d'un Demi-ton chromatique.
Le Double dièse (symbole = x) élève la Hauteur de deux Demi-tons chromatiques.
Le Bémol (symbole = b) abaisse la Hauteur d'un Demi-ton chromatique.
Le Double bémol (symbole = bb) abaisse la Hauteur de deux Demi-tons chromatiques.
Le Bécarre (symbole = une chaise penchée sans pieds derrière) annule l'effet de toutes les Altérations précédentes et redonne à la Note sa Hauteur d'origine.
Ces Altérations se mettent juste devant une Note dans le morceau musical (Altération accidentelle) ou juste derrière une Clef (Altération constitutive).
- L'Altération accidentelle concerne toutes les Notes de même Nom et de même Hauteur qui se trouvent après elle dans la même Mesure (voir Figure 1 ci-dessus).
Attention : Dans les partitions anciennes, l'Altération accidentelle n'est valable que pour la Note et non pour la Mesure.
L'Altération s'étend aux Notes liées de même Hauteur lorsque la Liaison de prolongation traverse une Barre de Mesure (voir Figure 2 ci-dessus).
Une Altération mise entre parenthèses indique une Altération de précaution visant à éviter toute ambiguïté (voir Figure 2 ci-dessus).
- L'Altération constitutive concerne toutes les Mesures du morceau musical et toutes les Notes de même Nom et de Hauteur quelconque, sauf si intervient une Altération accidentelle modifiant la Hauteur de la Note (voir Figure 3 ci-dessus pour laquelle toutes les Notes sont bémolisées sauf les Notes n° 4 et 6).
Pour les Dièses, leur ordre d'écriture sur la Portée est le sens horaire du Cycle des Quintes, c'est-à-dire par Quintes ascendantes comme suit : fa do sol ré la mi si (voir Figure 4 ci-dessus).
Pour les Bémols, leur ordre d'écriture sur la Portée est le sens anti-horaire du Cycle des Quintes, c'est-à-dire par Quintes descendantes comme suit : si mi la ré sol do fa (voir Figure 5 ci-dessus).
Un Accord de trois, quatre ou cinq notes est dit Altéré lorsque l'une de ses Notes est modifiée par une Altération accidentelle d'un Demi-ton chromatique (Dièse, Bémol ou Bécarre) et que l'Accord obtenu est nouveau.
Si on élève par exemple d'un Demi-ton chromatique la Tierce d'un Accord parfait mineur, on n'obtient rien d'autre qu'un Accord parfait majeur (déjà connu).
On parle donc d'Accord altéré uniquement quand la "Quinte d'un Accord de Tierce majeure est Altérée accidentellement", devenant ainsi Augmentée ou Diminuée.
Les seuls Accords pouvant être altérés sont donc les suivants :
- l'Accord parfait majeur,
- l'Accord de Septième de Dominante,
- l'Accord de Septième majeure,
- l'Accord de Neuvième de Dominante,
- l'Accord de Neuvième majeure et septième majeure.
(cf [LEOT])
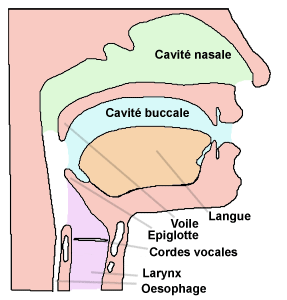
L'Appareil vocal comprend quatre éléments fondamentaux placés sous le contrôle du système nerveux central (voir Figure ci-dessus) :
- la Soufflerie, constituée d'un réservoir d'air (les poumons, actionnés par les muscles du thorax et de l'abdomen) et d'un tube (trachée artère) qui conduit l'air aux cordes vocales du larynx,
- le Vibrateur (larynx) qui engendre les ondes aériennes à travers la fente glottique en agissant sur les cordes vocales (vibration à la Fréquence Fondamentale F0 pour les sons voisés, ou maintien en position complètement relâchée pour les sons non-voisés),
- les Résonateurs (cavités pharyngienne, buccale, labiale et nasale) qui, en vibrant à leurs fréquences propres par phénomème de Résonance, produisent le Timbre de la voix,
- les Articulateurs (mâchoire inférieure, voile du palais et sa luette, langue, lèvres) qui modifient la forme des Résonateurs et en conséquence la forme de l'onde laryngée. Dans certaines langues, les cordes vocales peuvent être utilisées comme articulateurs (coup de glotte) mais pas en français.
L'ensemble des Résonateurs constitue le Conduit vocal, une Caisse de résonance semblable au tube du cor ou au corps du violon. Il est délimité en amont du flux d'air par les cordes vocales et en aval par les lèvres et les narines.

L'Appogiature est un Ornement particulier (symbole = une ou plusieurs petites Notes placées juste avant une Note standard, voir Figure ci-dessus). Sa Durée est prélevée sur celle de la Note précédente (Appogiature non accentuée) ou sur celle de la Note suivante (Appogiature accentuée).
L'Armure (ou Armature) est un groupe d'Altérations constitutives (placées à la Clef) et caractéristique d'une Tonalité.
Voir Figure de Note.
Voir Appareil vocal.
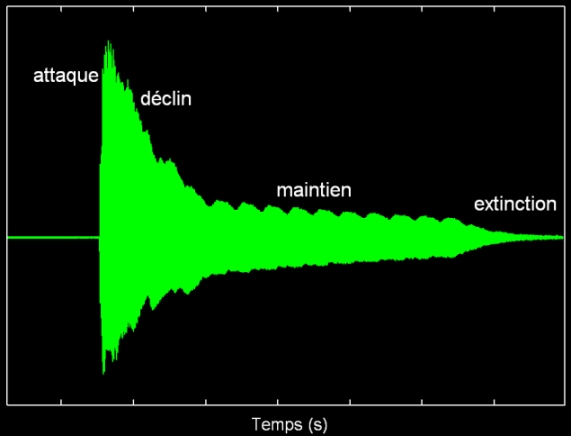
L'Attaque est la représentation temporelle d'un Son musical entre son début et l'atteinte de son amplitude maximale (voir Figure ci-dessus).
La durée de l'Attaque est appelée "Mordant ou Eclat", de l'ordre de 20 ms pour la trompette, 50 ms pour le piano, 300 ms pour le violon et 800 ms pour l'orgue (cf [GOY]).
L'attaque contribue fortement au Timbre. Ainsi, le Son enregistré d'un piano, rejoué en sens inverse, ressemble à celui d'un accordéon.
Voir Syllabe.
Un Accord de trois notes est dit Augmenté lorsque sa Tierce est majeure et sa Quinte haussée d'un Demi-ton (exemple : do - mi - sol#).
La Bande critique est la bande de Fréquences pour lesquelles l'oreille entend un Battement ou une impression désagréable de dureté sans Battement, lorsque deux Sons purs de Fréquences proches sont entendus.
La largeur de cette Bande critique est de 0,26 Octave (= log2(6/5)) correspondant à l'Intervalle "Tierce mineure" (de rapport 6/5 en Fréquence).
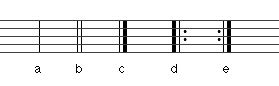
Les Barres de Mesure découpent la partition en petites sections (appelées Mesures), sections et morceaux.
Les différentes Barres de Mesure, toutes verticales, sont les suivantes (voir Figure ci-dessus) : Barre pointillée (division de Mesure), a) Barre simple (limite de Mesure), b) Barre double (limite de section), c) Barre de fin (fin de morceau), d) Barre de début de reprise (début de partie à jouer deux fois), e) Barre de fin de reprise (fin de partie à jouer deux fois).
Voir Portée.
La Basse d'un Accord est sa Note la plus grave.

Le Battement physique est l'onde acoustique résultant de la superposition de deux Sons purs de Fréquences proches (voir Figure ci-dessus).
Pour deux Sons purs tels que :
p1(t) = A1 sin (ω1 t + φ1) et p2(t) = A2 sin (ω2 t + φ2)
alors la résultante p(t) sera :
p(t) = (A1 + A2) sin(ωm t + φm) cos(ωd t + φd) + (A1 - A2) cos(ωm t + φm) sin(ωd t + φd)
avec :
ωm = (1/2) (ω1 + ω2)
ωd = (1/2) (ω1 - ω2)
φm = (1/2) (φ1 + φ2)
φd = (1/2) (φ1 - φ2)
Ainsi, la résultante de deux sinusoïdes équivaut à une sinusoïde de Fréquence égale à la moyenne de leurs Fréquences, multipliée (modulée) par une sinusoïde de Fréquence égale à la demi-différence de leurs Fréquences (appelée Fréquence du Battement).
Le Battement Psychoacoustique est la perception du Battement physique par l'oreille (voir Figure ci-dessus). La Fréquence de ce Battement est la différence de Fréquence des deux Sons (et non la demi-différence).
Voir Altération.
Voir Altération.
Voir Figure de Note.
La Brillance d'un Son ou Centre de Gravité Spectral (CGS) caractérise l'équilibre entre les graves et les aigus.
Un son brillant contient beaucoup de composantes de Fréquence aigües et a donc un CGS élevé. Au contraire, un son mat a un CGS faible.
Si Ak est l'amplitude de la composante spectrale de Fréquence fk d'un Son comportant N composantes, alors le CGS (en Herz) est défini par :
CGS = ∑k[fk Ak] / ∑k[Ak]
La Brillance contribue fortement au Timbre.
Le Bruit, en tant que stimulus physique, est défini de deux manières :
- par l'acoustique comme un Son complexe non périodique et dont les Fréquences, les amplitudes et les phases varient de façon aléatoire,
- par la psycho-acoustique comme la sensation d'Intensité sonore, pouvant être gênante voire néfaste à la santé, variant en fonction de l'Intensité, de la Fréquence, du Spectre sonore, du masquage, etc.
Le Chiffrage 4/4 des Mesures est parfois représenté par un "C", et le Chiffrage 2/2 par un "C" barré.


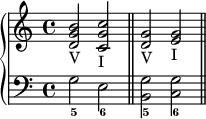


En Musique tonale, une Cadence (simple) est une progression harmonique d'un Accord vers un autre, destinée à marquer la fin d'une Phrase musicale par son caractère conclusif ou suspensif.
Marcel Bitsch, dans son Précis d'harmonie tonale (Editions musicales Alphonse Leduc, 1988), retient cinq types de Cadences :
Demi-cadence :
La Demi-cadence Enchaîne deux Accords, d'un Degré autre que V au Degré V (voir exemple en Figure 1 ci-dessus).
Par son caractère suspensif (attente de quelque chose), elle est semblable à la "virgule" d'une phrase littéraire.
Cadence rompue :
La Cadence rompue Enchaîne deux Accords, du Degré V à un Degré autre que I (voir exemple en Figure 2 ci-dessus).
Par son caractère suspensif (effet de surprise), elle relance la Phrase musicale selon un effet de surprise plus ou moins prononcé. Elle est semblable aux "deux points" d'une phrase littéraire.
Cadence imparfaite :
La Cadence imparfaite Enchaîne deux Accords, du Degré V au Degré I, l'un des deux au moins étant à l'état de Renversement (voir exemple en Figure 3 ci-dessus).
Par son caractère moyennement conclusif (repos passager), elle est semblable au "point-virgule" d'une phrase littéraire.
Cadence parfaite :
La Cadence parfaite Enchaîne deux Accords, du Degré V au Degré I, tous deux dans leur Etat fondamental (voir exemple en Figure 4 ci-dessus).
Par son caractère conclusif (repos complet), elle est semblable au "point" d'une phrase littéraire.
Cadence plagale ou Cadence d'église :
La Cadence plagale Enchaîne deux Accords, du Degré IV au Degré I, ce dernier étant à l'Etat fondamental (voir exemple en Figure 5 ci-dessus).
Par son caractère fortement conclusif (fin du morceau musical), elle est semblable au "point final" d'une phrase littéraire.
Dans un sens plus large, une Cadence désigne également une succession d'Accords, donc, en fait, une succession de Cadences simples.
La caisse de résonance (ou Résonateur) est la partie d'un Instrument instrumental ou vocal qui a pour rôle de recevoir et d'amplifier par Résonance le son produit par le Vibrateur.
Selon les Instruments, cette caisse est constituée par :
- Instruments à cordes : table d'harmonie et caisse.
- Instruments à vent : Tuyau sonore (qui est le Conduit vocal pour les Voix chantées ou parlées). Remarque : la colonne d'air contenue dans le tuyau est le véritable Résonateur, le métal du tuyau n'étant qu'un Résonateur accessoire (cf [BOU Propagation]).
- Percussion : corps creux relié au Vibrateur (caisse, coque, tuyau, etc.) ou corps du Vibrateur lui-même (exemple : triangle).
Les Fréquences propres de la caisse de résonance jouent un rôle important pour la qualité du son puisqu'elles filtrent les Fréquences produites par le Vibrateur, en renforçant certaines et en atténuant d'autres. On obtient ainsi le Timbre spécifique de l'Instrument.
Ainsi, dans le cas du violon, la table d'harmonie vibre selon ses Modes propres sous l'action de la Corde vibrante. Remarque : à la différence de la corde, les fréquences Propres de la table ne sont pas multiples entières les unes des autres (cf [CHAI, p.38]).
En musique occidentale, le Caractère est un terme qui indique la teinte générale donnée à l'expression d'une Phrase musicale ou d'un morceau entier d'une oeuvre musicale (cf [DAN, Théorie, parag. 266 et 223]).
Certains termes viennent en complément du Tempo (exemples : Affetuoso, Agitato, Cantabile, Con brio, Con spirito, Maestoso).
D'autres termes sont plus généraux et souvent poétiques (exemples : Amabile, Amoroso, Appassionato, Ardito, Brillante, Capriccioso, Con dolore, Tristamente).
Attention aux confusions possibles liées à la langue italienne : Par exemple :
- Le terme piano qui signifie doucement fait référence à la Nuance (intensité des Notes) et non au Tempo ;
- Le terme Allegro qui signifie gai fait référence au Tempo (durée des Temps) et non au Caractère.
Voir Figure de Note.
En musique classique, le Catalogue est spécifique d'un éditeur et regroupe l'ensemble des oeuvres d'un même compositeur, les oeuvres étant classées presque toujours par ordre chronologique.
Exemples :
- Jean-Sébastien Bach : catalogue "Bach Werke Verzeichnis" (sigle "BWV") établi dans les années 1950 par Wolfgang Schmieder.
- Johann Christian Bach : 18 catalogues différents dont catalogue "Warburton" (sigle "W"), appelé aussi "The Collected Works of Johann Christian Bach" (sigle "CW"), établi par Ernest Warburton, et catalogue "Terry" (sigle "T") établi par Charles Sanford Terry.
- Georg Friedrich Haendel : catalogue "Händel Werke Verzeichnis " (sigle "HWV") établi entre 1978 et 1986 par Bernd Baselt.
- Franz Liszt : deux catalogues différents dont catalogue "Searle" (sigle "S") établi par Humphrey Searle, et catalogue "Raabe" (sigle "R") ébli par Peter Raabe.
- Wolfgang Amadeus Mozart : catalogue "Köchel Verzeichnis" (sigle "KV") établi en 1861 par Ludwig von Köchel puis complété ensuite par d'autres musicologues.
- Franz Schubert : catalogue "Deutsch Verzeichnis" (sigle "D") établi par Otto Erich Deutsch.
Le sigle du catalogue est parfois suivi d'une lettre donnant le Genre musical de l'oeuvre selon l'éditeur du catalogue.
Ainsi, le "Concerto pour clavecin et orchestre à cordes en fa mineur" de Johann Christian Bach peut être référencé "W C73" ou "W. C73", la lettre "C" désignant le Genre "Musique orchestrale" selon l'éditeur Warburton.
Le catalogue est ensuite suivi du numéro de l'oeuvre, qui est généralement le numéro d'Opus et plus rarement un numéro d'oeuvre attribué par l'éditeur du catalogue.
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
Voir Cycle des quintes.
Voir Voix.


Le Chiffrage classique des Accords (appelé "basse continue") se fait directement sur la Portée comme suit :
Les Chiffres (voir Figure 1 ci-dessus) :
Chaque Chiffre désigne un Intervalle ("2" pour une Seconde, "3" pour une Tierce, "4" pour une Quarte, "5" pour une Quinte, etc.) par rapport à la Basse et non pas par rapport à la Fondamentale.
Par exemple, dans la troisième Mesure de la Figure 1 ci-dessus, le chiffrage de l'Accord sol - do - mi (Renversement de do - mi - sol dont la Fondamentale est do) comprend deux Chiffres, un "4" et un "6" placés au-dessus du sol de la Basse. Le "4" signifie une Quarte et représente la Fondamentale do. Le "6" signifie une Sixte et représente la Tierce mi.
- Les Chiffres sont disposés ordinairement de manière ascendante et par ordre croissant : 2, 3, 4, 5, etc. (exemple A).
- La réalisation de l'Accord au-dessus de la Note de Basse est alors laissée au libre choix de l'exécutant, lequel peut Supprimer ou Doubler la Note qu'il veut, opter pour la Position serrée ou large, Redoubler éventuellement certains Intervalles, etc. (exemple B).
- Si les Chiffres ne se suivent pas dans l'ordre croissant, c'est que l'Accord réclame une Disposition spéciale, voulue, soit par le compositeur lui-même (exemple C), soit par les propres règles de réalisation de ce type d'Accord (cas des Accords de cinq notes).
- Un Chiffre barré indique un Intervalle diminué, essentiellement Quinte ou Septième (exemple D).
- Certains Chiffres peuvent être sous-entendus. C'est le cas fréquent de la Tierce (exemple E) ou de la Quinte juste de la Basse (exemple F).
Les Altérations et autres symboles (voir Figure 2 ci-dessus) :
- Une Altération devant un Chiffre affecte la Note représentée par ce Chiffre (exemple A).
- Une Altération non suivie d'un Chiffre affecte la Tierce de la Basse qui est alors sous-entendue (exemple B).
- Certaines Altérations peuvent être sous-entendues (essentiellement dans les Accords de quatre et cinq Notes placés sur la Dominante).
- Une petite croix (+) devant un Chiffre représente la Sensible (exclusivement dans les Accords de Septième et Neuvième de Dominante). Elle est placée devant le Chiffre de l'Intervalle correspondant à cette Sensible (exemple C).
- Une ligne horizontale après un Chiffre indique la prolongation d'une ou plusieurs Notes de l'Accord, sans interdire d'éventuels changements de Position (exemple D).
- Une ligne horizontale avant un Chiffre est employée exceptionnellement pour le Chiffrage du retard de la Basse.
- Un zéro indique une absence d'harmonie (exemple E).
- Un Chiffre romain (I, II, III, IV, etc.) sous les Chiffres de l'Accord indique parfois (en France) son Degré afin de lever certaines ambiguïtés (notamment le Chiffrage identique des Degrés I et V pour les Accords de trois notes).
Voir détail dans Mesure.
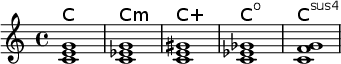
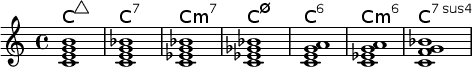
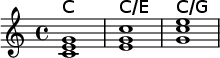


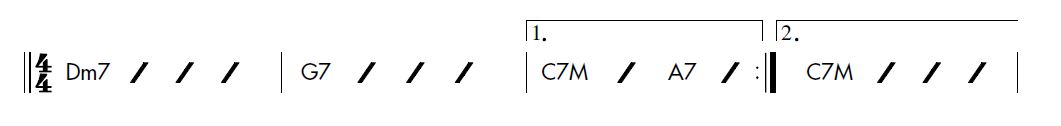


Figures ci-dessus : Figure 1 : Chiffrage moderne des accords ; Figures 2 et 3 : Chiffrage du rythme en tableau ; Figure 4 : Chiffrage du rythme en ligne ; Figures 5 et 6 : Chiffrage du rythme sur la portée
Le Chiffrage moderne des Accords (sous forme de grilles d'Accords en musique Jazz/Rock) n'est que partiellement standardisé. Il emploie les lettres de l'alphabet latin, les chiffres romains et des symboles spéciaux empruntés à la notation musicale et à l'alphabet grec. Ce Chiffrage moderne est le suivant :
Chiffrage des Accords :
- La Fondamentale de l'Accord est la Note dont le Nom est une lettre selon la notation anglo-saxonne (A pour la, B pour si, C pour do... G pour sol).
- Le qualificatif de l'Accord est défini par un symbole spécifique (voir Figure 1 de gauche ci-dessus et Tableau 1ère partie ci-dessous).
- La quatrième Note d'un Accord de quatre notes est défini par un symbole spécial (voir Figure 1 de milieu ci-dessus et Tableau 2ème partie ci-dessous).
- La cinquième Note d'un Accord de cinq notes est défini également par un symbole spécial (voir Tableau 3ème partie ci-dessous).
- Les Renversements sont définis par deux indications séparées d'une barre oblique (voir Figure 1 de droite ci-dessus et Tableau 4ème partie ci-dessous) : la Fondamentale de l'Accord et la Note la plus grave du Renversement, c'est-à-dire la Note qui a la Fonction de Basse à la place de la Fondamentale.
- La formule de l'Accord est défini par une séquence de symboles basée sur les Intervalles constitutifs de l'Accord et leurs Altérations éventuelles :
Ces Intervalles (définis à partir de la Fondamentale) sont codés par un chiffre correspondant aux Intervalles de la Gamme Majeure (1 pour Unisson, 2 pour Seconde majeure, 3 pour Tierce majeure... 9 pour Neuvième majeure). Les Altérations usuelles spécifient les Intervalles altérés. Ainsi, la Triade Mineure do - mib - sol est codée par la séquence 1 - b3 - 5.
- Le Degré de l'Accord est le Degré de sa Fondamentale. Les différents Degrés sont ceux des Degrés usuels, en ajoutant les Altérations éventuelles.
Le Tableau suivant donne les symboles des qualificatifs usuels des Accords.
| Symbole | Qualificatif de l'Accord | Exemple | Formule |
|---|---|---|---|
| pas de symbole | Majeur | C | 1 - 3 - 5 |
| -, m ou min | Mineur | C- | 1 - b3 - 5 |
| + ou aug | Augmenté | C+ | 1 - 3 - #5 |
| ° ou dim | Diminué | C° | 1 - b3 - b5 |
| sus ou sus4 | Suspendu | Csus | 1 - 4 - 5 |
| 7 | Septième de dominante | C7 | 1 - 3 - 5 - b7 |
| -7 ou min7 ou m7 | Septième mineure | C-7 | 1 - b3 - 5 - b7 |
| Φ ou -7b5 | Septième mineure et Quinte diminuée | CΦ | 1 - b3 - b5 - b7 |
| Δ ou maj7 ou M7 ou j7 | Septième majeure | CΔ | 1 - 3 - 5 - 7 |
| dim7 | Septième diminuée | Cdim7 | 1 - b3 - b5 - bb7 |
| -Δ ou -maj7 ou min(maj7) | Septième majeure et Parfait mineur | C-Δ | 1 - b3 - 5 - 7 |
| maj7#5 | Septième majeure et Quinte augmentée | Cmaj7#5 | 1 - 3 - #5 - 7 |
| 6 | Sixième | C6 | 1 - 3 - 5 - 6 |
| -6 | Sixième mineure | C-6 | 1 - b3 - 5 - 6 |
| sus | Suspendu | C7sus4 | 1 - 4 - 5 - b7 |
| add | Avec Note ajoutée | Cadd2 | 1 - 2 - 3 - 5 |
| 9 ou 7/9 | Neuvième majeure de dominante | C9 | 1 - 3 - 5 - b7 - 9 |
| b9 ou 7/b9 | Neuvième mineure de dominante | Cb9 | 1 - 3 - 5 - b7 - b9 |
| -9 ou -7/9 | Neuvième majeure et Septième mineure | C-9 | 1 - b3 - 5 - b7 - 9 |
| -7b9 | Neuvième mineure et Septième mineure | C-7b9 | 1 - b3 - 5 - b7 - b9 |
| -7b5b9 | Neuvième mineure et Quinte diminuée | C-7b5b9 | 1 - b3 - b5 - b7 - b9 |
| maj9 ou maj7/9 | Neuvième majeure et Septième majeure | Cmaj9 | 1 - 3 - 5 - 7 - 9 |
| maj7#9 ou maj7#9 | Neuvième augmentée | Cmaj7#9 | 1 - 3 - 5 - 7 - 9# |
| dim7b9 | Neuvième mineure et Septième diminuée | Cdim7b9 | 1 - b3 - b5 - bb7 - b9 |
| -maj9 ou -(maj7/9) | Neuvième majeure, Septième majeure et Parfait mineur | C-maj9 | 1 - b3 - 5 - 7 - 9 |
| maj7#5/9 | Neuvième majeure et Quinte augmentée | Cmaj7#5/9 | 1 - 3 - #5 - 7 - 9 |
| / | Premier Renversement | C/E | 3 - 5 - 1 |
| / | Deuxième Renversement | C/G | 5 - 1 - 3 |
Chiffrage du rythme :
Trois formes de notation existent (cf [TOS]) : en tableau, en ligne ou sur la Portée :
Chiffrage en tableau :
Le tableau se présente sous forme de lignes de cases (voir Figure 2 ci-dessus), chaque case représentant une Mesure (de 4 Temps essentiellement), chaque ligne représentant une carrure (de 8 Mesures le plus souvent).
La notation peut être allégée par un silence (Figure de Pause répétant l'absence d'Accord dans la Mesure) et par des symboles de Répétition (une ou deux barres épaisses obliques et entourées de deux points, répétant la ou les deux Mesures précédentes).
Chaque case contient les Accords de la Mesure, symbolisés par leur Chiffrage, à raison de 4 Accords maximum par case.
Les cases sont alors sub-divisées par parties que l'on lit dans le sens des aiguilles d'une montre (voir Figure 3 ci-dessus).
Chiffrage en ligne :
La notation en ligne (voir Figure 4 ci-dessus) est plus précise. Elle consiste à noter les Accords dans leurs Mesures respectives (délimitées par une Barre de mesure). La barre oblique simple symbolise chaque Temps.
La notation peut être allégée par des symboles de Répétition.
Chiffrage sur la Portée :
La notation sur une Portée permet une grande précision rythmique. Deux notations sont possibles :
Cas 1 : La barre oblique simple représente le Temps et les Accords sont notés au-dessus de la Portée (voir Figure 5 ci-dessus).
Cas 2 : La barre oblique simple représente les Accords et les Durées de Note ou de Silence sont les symboles usuels (voir Figure 6 ci-dessus).
Voir définition dans Accord.


La Clef, placée en début de Portée, permet de déterminer le Nom et la Hauteur des Notes.
Les Clefs courantes sont les suivantes (voir Figure 1 ci-dessus) : la Clef de sol qui indique le sol de l'Octave 3, la Clef d'ut qui indique le do de l'Octave 3, et la Clef de fa qui indique le fa de l'Octave 2.
Des trois Clefs, celles de fa et de sol sont les plus utilisées (voir Figure 2 ci-dessus).
Voir Répétition.
Voir Syllabe.
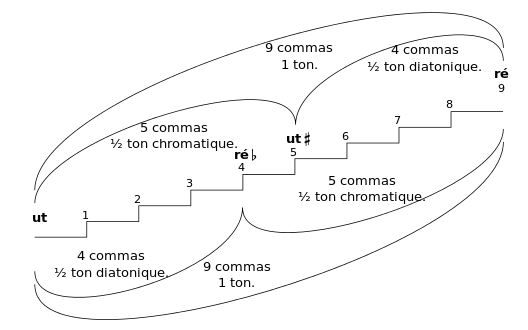
Le Comma est un Intervalle très petit défini entre deux séquences d'Intervalles purs.
Le Comma pythagoricien entre 12 Quintes et 7 Octaves vaut (3/2)12/27 = 312 / 219 = 1,0136.
Le Comma zarlinien ou syntonique entre 1 Ton majeur et 1 Ton mineur vaut (9/8)/(10/9) = 81/80 = 1,0125.
Le Comma Enharmonique ou petit diésis entre 1 Octave et 3 Tierces majeures vaut 2/(5/4)3 = 128/125 = 1,0240.
Ainsi, dans la Gamme chromatique à 17 Notes, entre les Notes do et ré se trouvent deux Notes intermédiaires : réb et, un Comma plus haut, do# (voir Figure ci-dessus cf [DAN]).
Dans la Gamme tempérée, on ne trouvera dans cet Intervalle qu'une seule Note intermédiaire (réb, do#, ou une autre Hauteur).
Voir Figure de Note.
Voir Appareil vocal.
Un Mouvement mélodique Conjoint est une suite de deux Notes de Nom différent et situées entre deux Degrés voisins de la Gamme diatonique. Exemples : (do# - ré) ; (mi - fa).
La Seconde augmentée (exemple : fa - sol#), bien qu'étant théoriquement un Intervalle mélodique Conjoint, est apparenté à un Intervalle mélodique Disjoint. En pratique, l'Intervalle mélodique Conjoint est donc inférieur ou égal à la Seconde majeure (soit un Ton).
La Tierce diminuée (exemple : do# - mib), bien qu'équivalente au Ton par Enharmonie, est aussi un Intervalle mélodique Disjoint (les Degrés étant non voisins).


En musique, la Consonance est la combinaison de Sons, telle un Intervalle ou un Accord, perçue comme agréable à l'oreille.
Cette perception ne dépend pas du rapport entre les Fondamentales des Sons considérés, mais de la concordance entre les séries Harmoniques de chacun des Sons composant l'Intervalle ou l'Accord.
Consonance des Intervalles :
Le Tableau suivant donne la liste des Intervalles Consonants avec leurs noms, leurs Notes (en do Majeur), le rapport idéal des Fréquences et le nombre de Demi-tons dans la Gamme diatonique.
Les Intervalles les plus Consonants sont alors : l'Unisson (rapport 1/1), l'Octave (rapport 2/1), la Quinte (rapport 3/2) et la Sixte majeure (rapport 5/3). Voir Figure 1 ci-dessus.
| Nom de l'Intervalle | Notes en do Majeur | Rapport idéal des Fréquences (a/b) | Nombre de Demi-tons (12 log2(a/b)) |
|---|---|---|---|
| Unisson | do - do | 1/1 | 0 |
| Tierce mineure | mi - sol | 6/5 | 3 |
| Tierce majeure | do - mi | 5/4 | 4 |
| Quarte juste | do - fa | 4/3 | 5 |
| Quinte juste | do - sol | 3/2 | 7 |
| Sixte mineure | mi - do | 8/5 | 8 |
| Sixte majeure | do - la | 5/3 | 9 |
| Octave | do - do à l'Octave | 2/1 | 12 |
Consonance des Accords de trois notes :
Les Accords de trois notes habituellement considérés comme les seuls Consonants sont les quatre Accords suivants, déjà utilisés au 16e siècle :
1- L'Accord parfait majeur, par exemple : do - mi - sol (voir Accord n°1 en Figure 2 ci-dessus), qui est l'empilement d'une Tierce majeure (do - mi) et d'une Tierce mineure (mi - sol).
2- L'Accord parfait mineur, par exemple : do - mib - sol (voir Accord n°4 en Figure 2 ci-dessus), qui est l'empilement d'une Tierce mineure (do - mib) et d'une Tierce majeure (mib - sol).
3- L'Accord de sixte majeure, par exemple : mib - sol - do (voir Accord n°5 en Figure 2 ci-dessus, 1er Renversement de l'Accord parfait mineur), qui est l'empilement d'une Tierce majeure (mib - sol) et d'une Quarte juste (sol - do).
4- L'Accord de sixte mineure, par exemple : mi - sol - do (voir Accord n°2 en Figure 2 ci-dessus, 1er Renversement de l'Accord parfait majeur), qui est l'empilement d'une Tierce mineure (mi - sol) et d'une Quarte juste (sol - do).
A noter que le groupement de trois Notes formant entre elles des Intervalles Consonants contribue, certes, à rendre l'Accord Consonant mais ne le garantit pas toujours. Par exemple, la Quarte juste peut rendre l'Accord légèrement Dissonant quand elle est en Basse de l'Accord.
Consonance des Accords de plus de trois notes :
Les Accords de plus de trois notes sont tous Dissonants.
Voir Phonème.
Le Contrepoint rigoureux (souvent appelé Contrepoint) est une forme d'écriture musicale qui consiste en une superposition organisée de Lignes mélodiques distinctes, l'"Accord" n'étant alors que le résultat fortuit de la simultanéité d'Intervalles harmoniques produite par cette superposition.
Les règles du Contrepoint sont plus restrictives que celles de l'Harmonie. Par exemple, les Accords pratiqués sont uniquement les Accords parfaits à l'Etat fondamental ou au premier Renversement. La Quarte sur la Basse, qui provoque un second Renversement, est cependant possible à titre de broderie ou de Note de passage.
Le Contrepoint, utilisé depuis la Renaissance jusqu'au milieu du 18e siècle, a fait place ensuite à l'art de l'Harmonie.
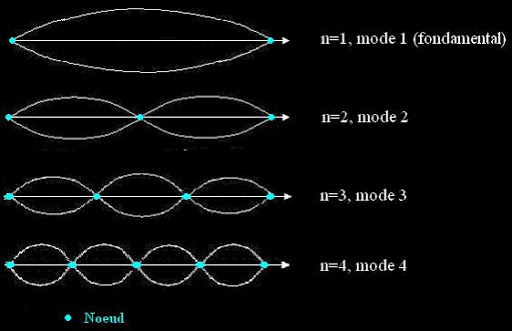
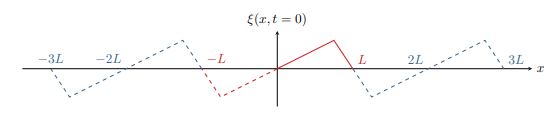
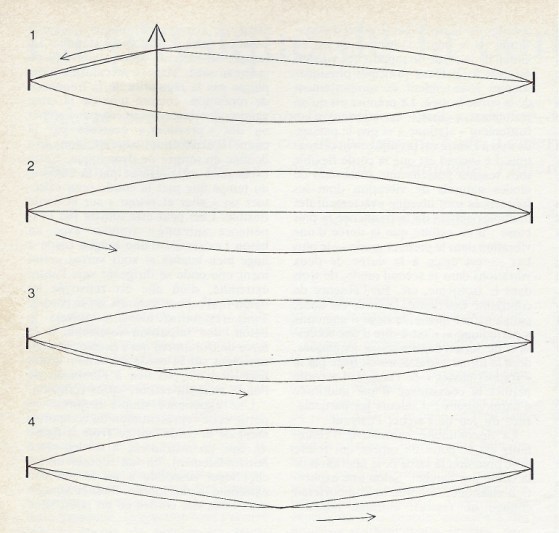
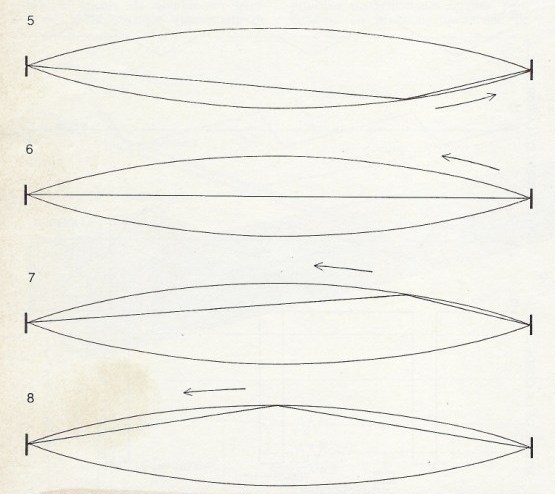
Au niveau acoustique, lorsqu'on fait vibrer une corde tendue entre deux points fixes, une onde transversale parcourt la corde deux fois, une fois dans chaque sens.
Lorsque la corde est en oscillation libre (en la pinçant ou la frappant par exemple), elle vibre à la Fréquence Fondamentale f0 selon une vibration non sinusoïdale composée d'une somme de vibrations sinusoïdales correspondant aux Fréquences propres f0, 2 f0, 3 f0... de la corde (voir Figure 1 ci-dessus représentant les quatre premiers Modes de vibration en amplitude).
Fréquence de chaque vibration sinusoïdale :
La Fréquence f de chaque vibration sinusoïdale vaut :
f = (1/2) n c/L
n est le rang de la Fréquence Harmonique (n = 1 pour la Fondamentale f0),
c est la vitesse de propagation de l'onde transversale le long de la corde (en m/s).
L est la longueur de la corde (en m).
Cette vitesse c vaut par ailleurs :
c = (T / M)1/2
T est la tension de la corde (en N),
M est la masse linéaire de la corde (en kg/m).
D'où la relation générale :
f = (1/2) n (1/L) (T/M)1/2
Le guitariste par exemple change continuellement la position des doigts sur les cordes en faisant varier leur longueur utile L comprise entre le chevalet et le doigt. Il peut aussi introduire des variations mineures (Vibrato) en faisant vibrer le doigt qui tient la corde.
Equation de la vibration de la corde en oscillation libre :
L'amplitude y(x, t) de la corde en fonction de l'espace (x) et du temps (t) s'écrit comme suit (cf [THIB, p.24] [LABA, p.37]) :
y(x, t) = ∑k=1,+∞[ ( Ak cos(2 π k f0 t) + Bk sin(2 π k f0 t) ) sin(π k x/L) ]
pour laquelle les conditions limites suivantes sont respectées : y(x = 0, t) = 0 et y(x = L, t) = 0
L'onde transversale de la corde est donc une combinaison linéaire d'ondes Stationnaires, mais sans que l'onde soit elle-même Stationnaire (cf [THIB, p.27]).
Les coefficients Ak et Bk dépendent des conditions initiales de la corde (à t = 0).
La forme initiale imposée à la corde est représentée sur la Figure 2 ci-dessus (cas d'une corde pincée, par exemple sur une guitare ou une harpe). La corde réelle est située entre x = 0 et x = L, représentée en traits pleins rouges. Les conditions initiales sont alors définies par les fonctions suivantes :
y(x, t = 0) = ∑k=1,+∞[ Ak sin(π k x/L) ]
(dy/dt)(x, t = 0) = ∑k=1,+∞[ Bk 2 π k f0 sin(π k x/L) ]
Les coefficients Ak et Bk s'identifient donc aux coefficients de la Décomposition en série de Fourier de ces deux fonctions et valent :
Ak = (2/L) ∫L0[ sin(π k x/L) y(x, t = 0) dx ]
Bk = (2/(k π c)) ∫L0[ sin(π k x/L) (dy/dt)(x, t = 0) dx ]
Remarque : Pour être dans le cadre mathématique exact des séries de Fourier, il est nécessaire de prolonger les fonctions y(x, t = 0) et (dy/dt)(x, t = 0) comme représenté sur la Figure 2 ci-dessus, à savoir :
- par imparité, en traits pointillés rouge sur l'intervalle [-L, 0], car la Décomposition en série de Fourier des fonctions y(x, t = 0) et (dy/dt)(x, t = 0) ne contient que des sinus.
- par périodicité de Période 2L, en traits pointillés bleus sur les intervalles [-∞, -L] et [L, +∞].
Equation de la vibration de la corde en oscillation forcée :
Cas du vibreur motorisé (cf [THIE, pp 26-27]) :
On force l'extrémité de la corde située en x = 0 à osciller à une Fréquence F fixée de l'extérieur et selon une amplitude y(x = 0, t) égale à : A cos(2 π F t)
L'amplitude y(x, t) de la corde en fonction de l'espace (x) et du temps (t) s'écrit alors comme suit :
y(x, t) = A cos(2 π F t) sin(2 π F (L - x)/c) / sin(2 π F L/c)
pour laquelle les conditions limites suivantes sont respectées : y(x = 0, t) = A cos(2 π F t) et y(x = L, t) = 0
Les termes spatial (x) et temporel (t) étant découplés, l'amplitude y(x, t) de la corde est l'équation d'une onde Stationnaire dont les noeuds sont espacés d'une distance Δx = (1/2) c/F.
Par ailleurs, lorsque F = (1/2) n c/L, c'est-à-dire lorsque la Fréquence de forçage F correspond à une Fréquence propre n f0 de la corde, la corde se met en Résonance. L'amplitude y(x, t) tend alors vers l'infini jusque la limite permise par la corde selon ses possibilités d'amortissement.
Cas de la corde frottée (cf [SCHEL]) :
Durant la plus grande partie de chaque vibration, la corde est entraînée par l'archet. Ensuite, elle s'en sépare brusquement et rebondit, pour être à nouveau saisie par une autre partie de l'archet et entraînée plus loin. La forme réelle de la corde est celle d'une ligne droite coudée en un point qui se déplace à chaque vibration sur une enveloppe constituée de deux paraboles peu accentuées (voir Figures 3 et 4 ci-dessus). Pour la corde la à vide d'un violon, ce point se déplace 440 fois par seconde. Ce mouvement particulier est une forme d'onde Stationnaire.
Voir Figure de Note.
Voir Portée.
Voir Voix.
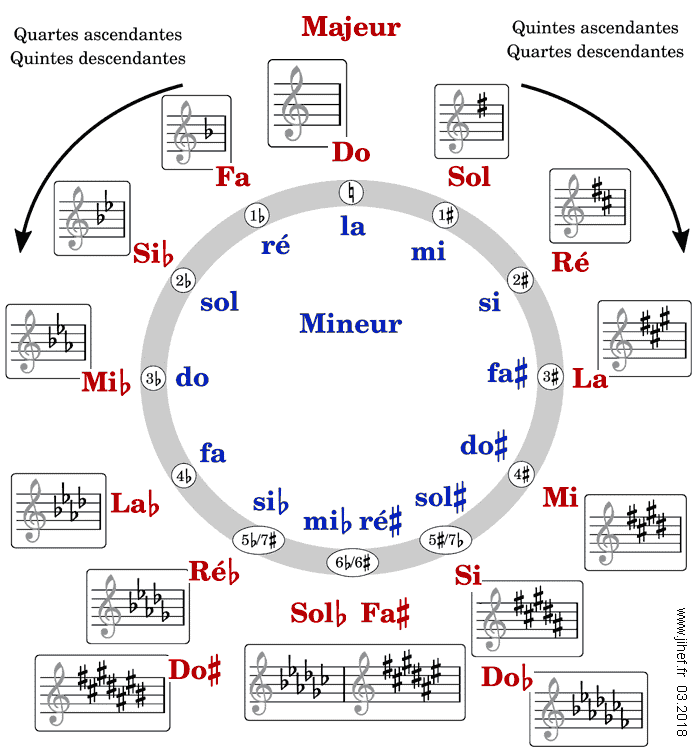
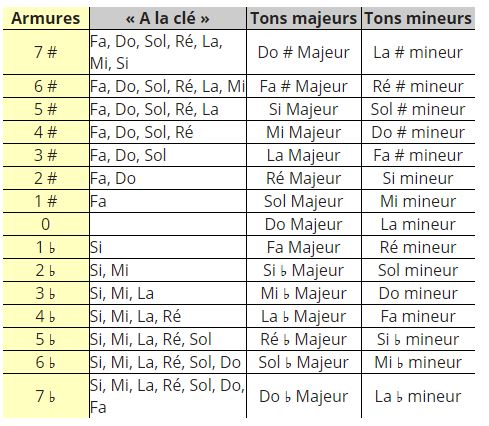
En théorie de la musique, le Cycle des quintes (ou Cercle des quartes) est un outil visuel riche en utilisations (voir Figures ci-dessus). Il montre la relation entre les 12 Degrés de la Gamme chromatique, par Intervalles de Quintes ou de Quartes, leurs Altérations correspondantes et la Tonalité Majeure ou Mineure associée.
Dans la Gamme tempérée, en commençant par une Note quelconque et en montant par Intervalles de Quintes justes, on passe par toutes les Notes de la Gamme chromatique avant de retomber sur la Note initiale au bout de sept Octaves (voir Figures ci-dessus) :
- Dans le sens horaire, le passage se fait par Quintes justes successives ascendantes de largeur 3,5 Tons ou par Quartes justes successives descendantes de largeur 2,5 Tons (exemple : do sol ré la...).
- Dans le sens anti-horaire, c'est l'inverse, les Quintes étant descendantes et les Quartes ascendantes (exemple : do fa sib mib...).
Le Cycle des Quintes permet de voir ainsi clairement l'ensemble des 15 Tonalités Majeures, ainsi que leurs relatives Mineures.
Par ailleurs, chaque Tonalité est représentée par un nombre d'Altérations (Dièses ou Bémols), entre 0 et 7, indiquées au niveau de l'Armure de la Clef (exemple : 2 Dièses pour la Tonalité ré majeur).
- En Gamme Majeure et en Gamme Mineure naturelle, à chaque passage de Quinte ascendante, ce nombre est incrémenté de 1 pour la raison remarquable que, quelle que soit l'Armure, on trouvera toujours dans chaque Octave deux Demi-tons diatoniques isolés encadrant alternativement deux et trois Tons (voir Gamme diatonique de Pythagore).
- Pour les autres Gammes Mineures (harmoniques ou mélodiques), cela reste encore vrai vu que l'Armure de toute Tonalité Mineure est en fait celle de la Gamme mineure naturelle, les Altérations provenant des autres Gammes Mineures (harmoniques ou mélodiques) étant considérées comme Accidentelles et ne figurant pas à la Clef.
- A noter que les Tonalités à 7 Dièses ou 7 Bémols sont peu utilisées en tant que Tonalité principale. On préfère leurs Tonalités Enharmoniques respectivement à 5 Bémols et 5 Dièses.
Voir Répétition.
Voir Répétition.
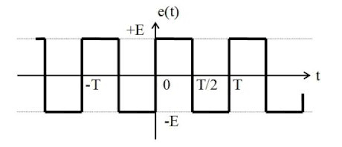
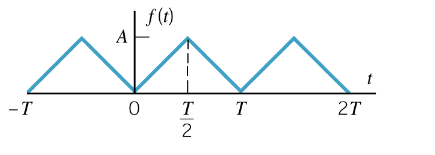
Toute onde périodique de Période T se décompose de façon unique en une somme d'ondes sinusoïdales dont les Fréquences sont des multiples entiers d'une même Fréquence f (appelée Fondamentale).
Ainsi, tout Son musical de pression acoustique p(t) et de Période T (c'est-à-dire tel que : p(t + T) = p(t)) peut se décomposer sous la forme :
p(t) = A0 + A1 cos (ω t) + B1 sin (ω t) + ... + An cos (n ω t) + Bn sin (n ω t) + ...
avec :
ω = 2 π/T = 2 π f
A0 = (1/T) ∫T/2-T/2[ p(t) dt ]
An = (2/T) ∫T/2-T/2[ p(t) cos(n ω t) dt ]
Bn = (2/T) ∫T/2-T/2[ p(t) sin(n ω t) dt ]
Si p(t) est impaire sur l'intervalle [-T/2, T/2] (c'est-à-dire tel que : p(-t) = -p(t)), alors : A0 = 0 et An = 0
Si p(t) est paire sur l'intervalle [-T/2, T/2] (c'est-à-dire tel que : p(-t) = p(t)), alors : Bn = 0
Quel que soit p(t), on démontre également que : An et Bn → 0 quand n → ∞
Exemple 1 (voir Figure ci-dessus) : Le signal e(t) en forme de créneau ( e(t) = -E pour -(T/2) < t < 0 et e(t) = E pour 0 < t < (T/2) ) se décompose en :
e(t) = 4 E π-1 ( sin(ω t) + ... + (2n - 1)-1 sin((2n - 1) ω t) + ... )
e(t) est donc la superposition d'une onde sinusoïdale de Fréquence Fondamentale f = 1/T et d'une somme infinie d'ondes sinusoïdales de Fréquences Harmoniques à rang impair (3f, 5f, 7f, etc.).
Démonstration (cf [CHO]) :
Calcul de A0 : La fonction e(t) est impaire donc A0 = (1/T) ∫T/2-T/2[ e(t) dt ] = 0
Calcul de An : La fonction e(t) est impaire donc An = (2/T) ∫T/2-T/2[ e(t) cos(n ω t) dt ] = 0
Calcul de Bn : Bn = (2/T) ∫T/2-T/2[ e(t) sin(n ω t) dt ] = (4/T) ∫T/20[ e(t) sin(n ω t) dt ] = (4 E/T) (n ω)-1 [ -cos(n ω t) ]T/20 = 2 E (n π)-1 (1 - cos(n π))
Si n est pair alors Bn = 0, et si n est impair alors Bn = 4 E (n π)-1
D'où le résultat : e(t) = 4 E π-1 ( sin(ω t) + ... + (2n - 1)-1 sin((2n - 1) ω t) + ... )
Exemple 2 (voir Figure ci-dessus) : Le signal f(t) en forme de triangle ( f(t) = -2 A (t/T) pour -(T/2) < t < 0 et f(t) = 2 A (t/T) pour 0 < t < (T/2) ) se décompose en :
f(t) = (A/2) - 4 A π-2 ( cos(ω t) + ... + (2n - 1)-2 cos((2n - 1) ω t) + ... )
f(t) est donc la superposition d'une constante (A/2), d'une onde sinusoïdale de Fréquence Fondamentale f = 1/T et d'une somme infinie d'ondes sinusoïdales de Fréquences Harmoniques à rang impair (3f, 5f, 7f, etc.).
Démonstration (cf [CHO]) :
Calcul de A0 : A0 = (1/T) ∫T/2-T/2[ f(t) dt ] = (2/T) ∫T/20[ 2 A (t/T) dt ] = 2 (A/T2) [ t2 ]T/20 = A/2
Calcul de Bn : La fonction f(t) est paire donc Bn = (2/T) ∫T/2-T/2[ f(t) sin(n ω t) dt ] = 0
Calcul de An : An = (2/T) ∫T/2-T/2[ f(t) cos(n ω t) dt ] = 8 A/T2 I = 2 A (ω/π)2 I
en posant : I = ∫T/20[ t cos(n ω t) dt ]
Intégrons I par parties. On pose : t = u et dv = cos(n ω t) dt. D'où : dt = du et v = (n ω)-1 sin(n ω t)
D'où I = [ u v ]T/20 - ∫T/20[ v du ] = (n ω)-1 [ t sin(n ω t) ]T/20 - (n ω)-1 ∫T/20[ sin(n ω t) dt ] = (n ω)-2 [ cos(n ω t) ]T/20 = (n ω)-2 (cos(n π) - 1)
D'où : An = 2 A (n π)-2 (cos(n π) - 1)
Si n est pair alors An = 0, et si n est impair alors An = -4 A (n π)-2
D'où le résultat : f(t) = (A/2) - 4 A π-2 ( cos(ω t) + ... + (2n - 1)-2 cos((2n - 1) ω t) + ... )
Voir Membrane vibrante.
Le Degré est le numéro d'ordre d'une Note dans une Gamme donnée, indépendamment de l'Altération de la Note.
L'intérêt de ce chiffrage est de pouvoir généraliser les Fonctions tonales dans toutes les Transpositions de Gammes Majeures et Mineures.
Dans la Gamme diatonique, le Degré s'applique aux sept Notes comme suit :
I. Tonique ; II. Sus-tonique ; III. Médiante ; IV. Sous-dominante ; V. Dominante ; VI. Sus-dominante ; VII. Sensible ou Sous-tonique ; VIII. Octave ou Tonique.
Ces noms caractérisent la position que les Degrés occupent dans la Gamme :
- La Tonique porte la Tonalité de la Gamme. Exemple : la Note Fa est la Tonique des Gammes de Fa Majeur et Fa Mineur.
- La Dominante est le degré le plus important après la Tonique.
- La Médiante tient le milieu entre la Tonique et la Dominante.
- La Sensible a une tendance qui la porte vers la Tonique dont elle n'est séparée que par un Demi-ton diatonique.
- Les autres Degrés portent leur nom de la place qu'ils occupent relativement à ces Degrés principaux.

Le Demi-ton est le plus petit des Intervalles Conjoints de la Gamme diatonique. Il est égal approximativement à la moitié du Ton, d'où son nom.
Le Demi-ton est chromatique lorsque les Notes ont même Nom et dont l'une est Altérée (c'est-à-dire situées entre un Degré et le même Degré Altéré). Exemples : (do - do#) ; (réb - ré).
Le Demi-ton est diatonique lorsque les Notes sont Conjointes (c'est-à-dire de Nom différent et situées entre deux Degrés voisins). Exemples : (do - réb) ; (do# - ré) ; (mi - fa).
L'Intervalle entre Demi-ton chromatique et Demi-ton diatonique est le Comma. Il s'agit implicitement du Comma pythagoricien.
Les musiciens considèrent généralement (voir exemple en Figure ci-dessus cf [DAN]) qu'un Demi-ton chromatique vaut (nc = 5) Commas, soit les 5/9 d'un Ton, et qu'un Demi-ton diatonique vaut (nd = 4) Commas, soit les 4/9 d'un Ton. Il s'agit implicitement du Demi-ton pythagoricien pour lequel on a :
Demi-ton chromatique : 2187/2048 = environ (1,0136)nc correspondant à l'Intervalle entre 7 Quintes et 4 Octaves (soit (3/2)7/24)
Demi-ton diatonique : 256/243 = environ (1,0136)nd correspondant à l'Intervalle entre 3 Octaves et 5 Quintes (soit 23/(3/2)5)
Comma pythagoricien : 1,0136 correspondant à l'Intervalle entre 12 Quintes et 7 Octaves (soit (3/2)12/27)
En Gamme tempérée, tous les Demi-tons sont égaux et valent : 1,05946 = 21/12.
Le Diapason est l'étalon musical actuel de la Hauteur. Il vaut 440 Hz et correspond à la Note "la" de l'Octave numéro 3.
Voir Altération.
Un Accord de trois notes est dit Diminué lorsque sa Tierce est mineure et sa Quinte baissée d'un Demi-ton (exemple : do - mib - solb).
Un Mouvement mélodique Disjoint est une suite de deux Notes de Noms différents et situées entre deux Degrés non voisins de la Gamme diatonique. Exemple : do# - mib.
L'Intervalle mélodique Disjoint est donc supérieur à la Seconde majeure.
La Dissonance est la non-Consonance.
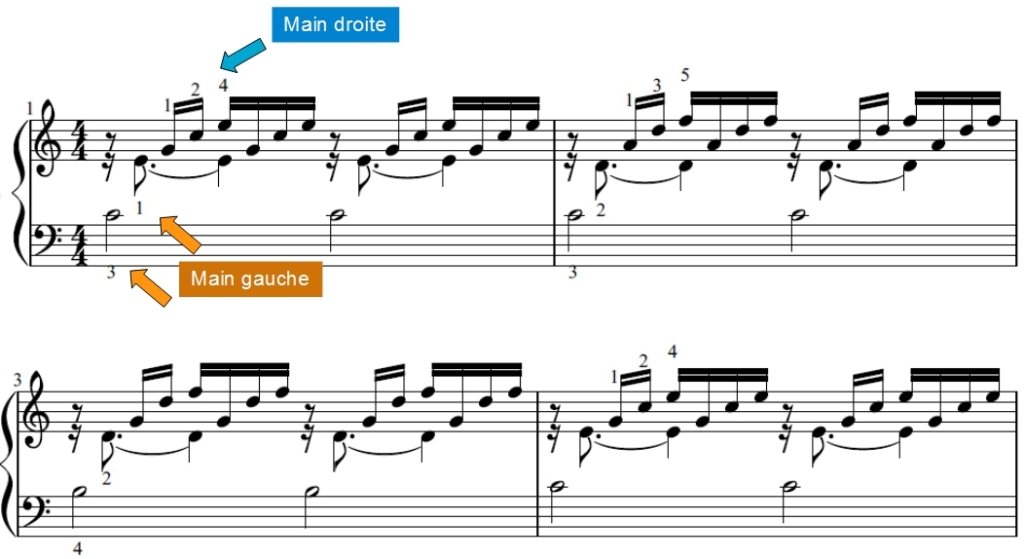
Le Doigté est un code à Chiffres qui indique les doigts à utiliser dans le jeu de certains Instruments.
Au piano :
Le code va de 1 (pouce) à 5 (auriculaire). Voir exemple en Figure ci-dessus (1er Prélude de J.S. Bach).
Le code n'est indiqué en général que lorsque la Main sort de sa position de base "Chaque doigt sur une touche consécutive".
Deux méthodes principales existent pour le choix des Doigtés : les experts privilégient les doigts agiles 2 3 et 4 dans le but d'obtenir un meilleur résultat sonore dans l'articulation des Notes. Les éditeurs et professeurs de piano choisissent plus systématiquement les Doigtés 3 4 et 5 qui favorisent l'aisance technique dans l'exécution des morceaux.
La technique du "Passage du pouce" permet de réutiliser les doigts pour atteindre de nouvelles touches. Deux mouvements sont possibles : 1° le pouce passe en dessous des doigts et joue la prochaine Note (par exemple quand la Main droite monte dans les aigus), 2° les doigts passent au-dessus du pouce et l'un deux joue la prochaine Note (par exemple quand la Main droite descend dans les graves).
D'autres techniques de Doigté existent mais sont rarement utilisées ou sont du domaine de l'expert. On peut citer :
- la "Substitution sur Note liée" (en changeant de doigt sur la même Note sans la répéter),
- la "Substitution sur Note répétée" (en doublant la Note avec un autre doigt),
- le "Glissé" (en jouant une Note voisine avec le même doigt),
- le "Chevauchement (ou croisement) des doigts" (en faisant passer un doigt au-dessus d'un autre),
- le "Passage du pouce au-dessus des doigts",
- l' "Arrangement entre les deux Mains" (en utilisant l'autre Main pour exécuter la Note).
Le Tableau suivant (cf [PHI]) donne pour chaque Main la succession naturelle des Codes lorsqu'on réalise une Gamme sur une Octave (par exemple en do Majeur : do, ré, mi... si, do, si, la... do).
Les symboles "point" et "apostrophe" désignent respectivement les mouvements n°1 et 2 du "Passage du pouce".
Les Notes Altérées (Dièse #, Double dièse x et Bémol b) sont indiquées en gras.
Sur les autres Instruments de musique :
- Instruments à cordes frottées (violon, violoncelle, etc.) : le code de la Main gauche est le suivant : 0 (corde à vide), n (pouce), 1 (index)... 4 (auriculaire).
- Instruments à cordes pincées : le code de la Main droite est soit l'initiale du doigt (p pour pouce, i pour index, m pour majeur, a pour annulaire et e pour auriculaire), soit un système de points (barre pour pouce, 1 point pour index, 2 points pour majeur, 3 points pour annulaire).
- Instruments à vents : le code indique quels trous doivent être obturés ou quelles clés actionnées.
| Gamme | Notes altérées "à la Clef" | Main gauche | Main droite |
|---|---|---|---|
| do majeur | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 | |
| sol majeur | (#) : fa | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| ré majeur | (#) : fa, do | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| la majeur | (#) : do, fa, sol | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| mi majeur | (#) : fa, sol, do, ré | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| si ou dob majeur | (#) : do, ré, fa, sol, la | 4 3 2 1 ' 4 3 2 1 2 3 4 . 1 2 3 4 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| fa# ou solb majeur | (#) : fa, sol, la, do, ré, mi | 4 3 2 1 ' 3 2 1 ' 2 . 1 2 3 . 1 2 3 4 | 2 3 4 . 1 2 3 . 1 3 1 ' 3 2 1 ' 4 3 2 |
| réb ou do# majeur | (b) : ré, mi, sol, la, si | 3 2 1 ' 4 3 2 1 ' 2 . 1 2 3 4 . 1 2 3 | 2 3 . 1 2 3 4 . 1 3 1 ' 4 3 2 1 ' 3 2 |
| lab majeur | (b) : la, si, ré, mi | 3 2 1 ' 4 3 2 1 ' 2 . 1 2 3 4 . 1 2 3 | 2 3 . 1 2 3 . 1 2 3 2 1 ' 3 2 1 ' 3 2 |
| mib majeur | (b) : mi, la, si | 3 2 1 ' 4 3 2 1 ' 2 . 1 2 3 4 . 1 2 3 | 3 . 1 2 3 4 . 1 2 3 2 1 ' 4 3 2 1 ' 3 |
| sib majeur | (b) : si, mi | 3 2 1 ' 4 3 2 1 ' 2 . 1 2 3 4 . 1 2 3 | 3 . 1 2 3 . 1 2 3 4 3 2 1 ' 3 2 1 ' 3 |
| fa majeur | (b) : si | 1 ' 4 3 2 1 ' 3 2 1 ' 2 3 . 1 2 3 4 . 1 | 1 2 3 4 . 1 2 3 4 3 2 1 ' 4 3 2 1 |
| la mineur harmonique | (#) : sol | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| mi mineur harmonique | (#) : fa, ré | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| si mineur harmonique | (#) : do, fa, la | 4 3 2 1 ' 4 3 2 1 2 3 4 . 1 2 3 4 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| fa# mineur harmonique | (#) : fa, sol, do, mi | 4 3 2 1 ' 3 2 1 ' 3 . 1 2 3 . 1 2 3 4 | 2 3 . 1 2 3 . 1 2 3 2 1 ' 3 2 1 ' 3 2 |
| do# mineur harmonique | (#) : do, ré, fa, sol, si | 3 2 1 ' 4 3 2 1 ' 3 . 1 2 3 4 . 1 2 3 | 2 3 . 1 2 3 . 1 2 3 2 1 ' 3 2 1 ' 3 2 |
| sol# ou lab mineur harmonique | (#) : sol, la, do, ré (x) : fa | 3 2 1 ' 4 3 2 x1 ' 3 . x1 2 3 4 . 1 2 3 | 2 3 . 1 2 3 . 1 x2 3 x2 1 ' 3 2 1 ' 3 2 |
| mib ou ré# mineur harmonique | (b) : mi, sol, la, si, do | 2 1 ' 4 3 2 1 ' 3 2 3 . 1 2 3 4 . 1 2 | 3 . 1 2 3 4 . 1 2 3 2 1 ' 4 3 2 1 ' 3 |
| sib ou la# mineur harmonique | (b) : si, ré, mi, sol | 2 1 ' 3 2 1 ' 4 3 2 3 4 . 1 2 3 . 1 2 | 3 . 1 2 3 . 1 2 3 4 3 2 1 ' 3 2 1 ' 3 |
| fa mineur harmonique | (b) : la, si, ré | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 4 . 1 2 3 4 3 2 1 ' 4 3 2 1 |
| do mineur harmonique | (b) : mi, la | 5 4 3 2 1 ' 3 2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 4 3 2 1 ' 3 2 1 |
| sol mineur harmonique | (#) : fa (b) : si, mi | 5 4 3 2 1 ' 3 #2 1 #2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 #4 5 #4 3 2 1 ' 3 2 1 |
| ré mineur harmonique | (#) : do (b) : si | 5 4 3 2 1 ' 3 #2 1 #2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 #4 5 #4 3 2 1 ' 3 2 1 |
| la mineur mélodique | 5 4 3 2 1 ' #3 #2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 #3 #4 5 4 3 2 1 ' 3 2 1 | |
| mi mineur mélodique | (#) : fa | 5 4 3 2 1 ' #3 #2 1 2 3 . 1 2 3 4 5 | 1 2 3 . 1 2 #3 #4 5 4 3 2 1 ' 3 2 1 |
| si mineur mélodique | (#) : do, fa | 4 3 2 1 ' 4 #3 #2 1 2 3 4 . 1 2 3 4 | 1 2 3 . 1 2 #3 #4 5 4 3 2 1 ' 3 2 1 |
| fa# mineur mélodique | (#) : fa, sol, do | 4 3 2 1 ' 3 #2 #1 ' 2 . 1 2 3 . 1 2 3 4 | 2 3 . 1 2 3 #4 . #1 3 2 1 ' 3 2 1 ' 3 2 |
| do# mineur mélodique | (#) : do, ré, fa, sol | 3 2 1 ' 4 3 #2 #1 ' 2 . 1 2 3 4 . 1 2 3 | 2 3 . 1 2 3 #4 . #1 3 2 1 ' 3 2 1 ' 3 2 |
| sol# ou lab mineur mélodique | (#) : sol, la, do, ré (x) : fa | 3 2 1 ' 3 2 #1 ' x4 3 #4 1 2 3 1 2 3 | 2 3 . 1 2 3 . #1 x2 3 #2 1 ' 3 2 1 ' 3 2 |
| mib ou ré# mineur mélodique | (b) : mi, sol, la, si | 2 1 ' 4 3 2 1 ' 3 2 b3 . b1 2 3 4 . 1 2 | 2 . 1 2 . 3 4 . 1 2 3 b2 b1 ' 4 3 2 1 ' 2 |
| sib ou la# mineur mélodique | (b) : si, ré, mi | 2 1 ' 3 2 1 ' 4 3 2 b3 b4 . 1 2 3 . 1 2 | 2 . 1 2 3 . 1 2 3 4 b3 b2 1 ' 3 2 1 ' 2 |
| fa mineur mélodique | (b) : la, si | 5 4 3 2 1 ' 3 2 1 b2 b3 . 1 2 3 4 5 | 1 2 3 4 . 1 2 3 4 b3 b2 1 ' 4 3 2 1 |
| do mineur mélodique | (b) : mi | 5 4 3 2 1 ' 3 2 1 b2 b3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 4 5 b4 b3 2 1 ' 3 2 1 |
| sol mineur mélodique | (#) : fa (b) : si | 5 4 3 2 1 ' 3 #2 1 2 b3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 #4 5 4 b3 2 1 ' 3 2 1 |
| ré mineur mélodique | 5 4 3 2 1 ' 3 #2 1 2 b3 . 1 2 3 4 5 | 1 2 3 . 1 2 3 #4 5 4 b3 2 1 ' 3 2 1 |
Voir Degré.
Dans un Accord, une Note Doublée est une Note qui y figure plusieurs fois. La Doublure se fait généralement par Octave et plus rarement par Unisson.
La Doublure est utilisée, par exemple, lorsqu'on écrit un Accord de trois notes à quatre Voix.
On double le plus souvent la Fondamentale d'un Accord, parfois sa Quinte, plus rarement sa Tierce.
Attention : Ne pas confondre avec le Redoublement.
En notation musicale, la Durée d'un Silence (en secondes) est caractérisée par une Figure de Silence, une Unité de Temps (voir Mesure) et un Tempo.
La Durée d'un Son musical est le laps de temps (en secondes) pendant lequel on peut entendre ses vibrations.
En notation musicale, la Durée d'une Note (en secondes) est caractérisée par une Figure de Note, une Unité de Temps (voir Mesure) et un Tempo.
A partir d'une Mélodie donnée à une Voix (en général celle du Soprano ou celle de la Basse), on crée les trois Voix restantes de manière à les faire sonner ensemble.
Il existe deux manières principales pour espacer harmonieusement les quatre Voix entre elles (Soprano, Alto, Ténor et Basse) :
- Position de quatuor : les Intervalles entre Parties sont à peu près égaux. C'est une position idéale qui sonne bien.
- Position de piano : la Partie Basse est isolée (comme la main gauche au piano) et les Parties supérieures sont groupées (main droite au piano).
Dans les deux cas, on ne doit pas dépasser l'Octave entre chacune des Parties supérieures. Mais cela est permis entre Basse et Ténor.





En Musique tonale, les Degrés peuvent, théoriquement, s'enchaîner les uns aux autres dans n'importe quel ordre. En pratique, les compositeurs ont construit une hiérarchie dans les Degrés.
L'Enchaînement le plus courant est le suivant : I (début) - IV (détente initiale) - V (effort) - I (détente conclusive). La Tonique initiale (I) peut être supprimée pour rendre l'entrée en matière encore plus saisissante.
Les fins de Phrase musicale font généralement l'objet de Cadences.
Pour les Accords de trois notes à l'Etat Fondamental, il existe 23 Enchaînements possibles (compte tenu des 12 Accords parfaits majeurs et des 12 Accords parfaits mineurs), qui se réduisent à seulement 3 types et 6 possibilités indépendemment de leurs Altérations et de la Tonalité du morceau musical (cf [FAB Unité 2.1] et [POU Pages Web]).
Ces 3 types sont les suivants (avec exemples donnés en Tonalité de do) :
Type d'Enchaînement à deux Notes communes :
L'Enchaînement peut se faire à la Tierce supérieure (do - mi - sol vers mi - sol - si) ou inférieure (do - mi - sol vers la - do - mi, voir Figure 1 ci-dessus).
Type d'Enchaînement à une seule Note commune :
L'Enchaînement peut se faire à la Quinte supérieure (do - mi - sol vers sol - si - ré, voir Figure 2 de gauche ci-dessus) ou inférieure (do - mi - sol vers fa - la - do, voir Figure 2 de droite ci-dessus).
Type d'Enchaînement à aucune Note commune :
L'Enchaînement peut se faire à la Seconde supérieure (do - mi - sol vers ré - fa - la, voir Figure 3 de gauche ci-dessus) ou inférieure (do - mi - sol vers si - ré - fa, voir Figure 3 de droite ci-dessus).
Les Enchaînements d'Accords font l'objet d'interdiction, sauf cas exceptionnel voulu par le compositeur. Par exemple :
- Les Quintes justes consécutives donnent une impression de dureté.
- Les Octaves justes et Unissons justes consécutifs appauvrissent l'harmonie par leur effet plat.
L'adjectif Enharmonique fait référence à des Notes dont les Hauteurs diffèrent d'un Comma dans la Gamme chromatique mais sont confondues dans la Gamme tempérée (exemple : sol# et lab).




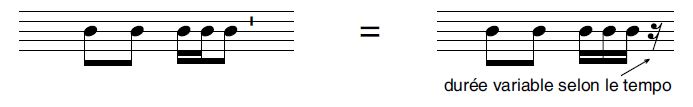

En notation musicale, les Figures de Note possibles pour une Note donnée sont les suivantes (voir haut de Figure 1 ci-dessus) : Carrée, Ronde, Blanche, Noire, Croche, Double croche, Triple croche, Quadruple croche, Quintuple croche.
Chaque Figure de Note a une durée (relative) valant le double de la suivante ou la moitié de la précédente.
Chaque Figure de Note possède une hampe, sauf les Rondes, soit une hampe vers le haut et à droite de la tête de Note, soit vers le bas et à gauche de la tête de Note (voir haut de Figure 2 ci-dessus).
Les hampes sont généralement ramenées vers le centre de la Portée pour un gain de place vertical et une meilleure lisibilité (voir haut de Figure 2 ci-dessus), sauf lorsqu'il y a deux Voix sur la même Portée, auquel cas la hampe des Notes est dirigée vers l'extérieur de la Portée pour éviter leur collision (voir bas de Figure 2 ci-dessus).
Chaque Figure de Note peut être éventuellement associée à :
- un ou plusieurs Points de prolongation ou d'augmentation (symbole = point, double point ou triple point placé juste après la Figure de Note), qui augmente la durée de la Figure de Note respectivement de la moitié, des trois quarts ou des sept huitièmes (voir Figure 3 de gauche ci-dessus),
- un Point d'orgue (symbole = point entouré d'un demi-cercle), qui prolonge la durée de la Figure de Note au gré de l'exécutant, avec suspension passagère du Tempo (voir Figure 3 de gauche ci-dessus),
- un Staccato (symbole = point placé au-dessus ou au-dessous de la tête de la Figure de Note), qui diminue légérement (en fonction du Tempo) la durée de la Figure de Note afin de la détacher de la suivante (voir Figure 3 de droite ci-dessus).
- un Comma (symbole = apostrophe ou petite virgule), Silence bref placé juste après une Figure de Note, et qui diminue légèrement sa durée (en fonction du Tempo). Voir Figure 4 ci-dessus.
- un Accord arpégé (symbole = ligne ondulée verticale) dont les Notes sont jouées successivement et rapidement comme pour une Appogiature (voir Figure 5 ci-dessus),
- un Doigté, qui indique le doigt à utiliser dans le jeu de certains Instruments.


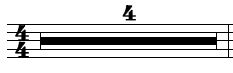
En notation musicale, les Figures de Silence possibles pour un Silence donné sont les suivantes (voir bas de Figure 1 ci-dessus) : Bâton de pause, Pause, Demi-pause, Soupir, Demi-soupir, Quart de soupir, Huitième de soupir, Seizième de soupir, Trente-deuxième de soupir.
Chaque Figure de Silence a une durée (relative) valant le double de la suivante ou la moitié de la précédente. Cette durée est égale à celle de la Figure de Note correspondante (voir Figure 1 ci-dessus).
Un Silence couvrant une Mesure entière est indiqué par une Pause centrée dans la Mesure (voir Figure 2 de gauche ci-dessus).
Un Silence couvrant plusieurs Mesures est indiqué par une longue barre centrée dans la Mesure et surmontée d'un chiffre donnant le nombre de Mesures (voir Figure 2 de droite ci-dessus).
Chaque Figure de Silence peut être éventuellement associée à :
- un ou plusieurs Points de prolongation ou d'augmentation (point, double point ou triple point placé juste après la Figure de Silence), qui augmente la durée de la Figure de Silence respectivement de la moitié, des trois quarts ou des sept huitièmes,
- un Point d'orgue ou point d'arrêt (symbole = point entouré d'un demi-cercle ou d'un U), qui prolonge la durée de la Figure de Silence au gré de l'exécutant, avec suspension passagère du Tempo.
Voir Répétition.
En Musique tonale, la Fonction Tonale prolonge la notion de Degré en décrivant les relations entre les Notes ou entre les Accords. Par exemple :
- la Tonique (Degré I) est conclusive (point de repos)
- la Sus-tonique (Degré II) est préparatrice (point de transition)
- la Médiante (Degré III) apporte la couleur Modale (Majeure ou Mineure)
- la Sous-dominante (Degré IV) est préparatrice (point de transition)
- la Dominante (Degré V) est suspensive (point d'attente)
- la Sus-dominante (Degré VI) est attirée par sa gamme mineure relative (qui commence sur le VI et utilise les mêmes Notes que la Tonalité de la Tonique)
- la Sensible (Degré VII) est attirée par la Tonique
Les Fonctions tonales sont réparties ordinairement en quatre familles de Degrés (cf [FAB Le mineur]) :
- Les Degrés principaux (dits "forts") : I, IV et V, qui expriment l'équilibre du Ton par des Quintes (I = pilier neutre, IV = Quinte inférieure de I, V = Quinte supérieure de I).
- Les Degrés secondaires : II et VI, qui prolongent ces Quintes.
- Les Degrés faibles : III, qui est ambigu et rarement utilisé.
- Les Degrés mixtes : VII, qui peut être fort ou faible selon son utilisation ou non avec la Tonique I.
Attention : Percevoir les Fonctions de ces Degrés nécessite une grande pratique de la Musique tonale.
En particulier, les Accords s'utilisent comme Fonction dans leur contexte tonal (cf [FAB Unité 7]) et s'obtiennent par Harmonisation de la Gamme diatonique qui les porte.
Les Figures relatives aux Accords de trois notes, Accords de quatre notes et Accords de cinq notes, montrent le résultat de cette Harmonisation dans le cas de la Gamme de do majeur et de la Gamme de do mineur harmonique.
Voir définition dans Accord.

La Note Fondamentale d'un Accord est la Note dite "de base" sur lequel est construit l'Accord.
Cette Note de base est la Basse de l'Accord après mise "à l'état fondamental réduit" obtenue en abaissant les Notes supérieures d'une Octave jusqu'à obtenir un empilement de Tierces (exemples : do - mi - sol ; do - mib - sol ; do - mi - sol - sib - ré).
Sur la Figure ci-dessus, les trois derniers Accords (do - sol - mi, mi - sol - do, et sol - do - mi) ont pour Accord à l'état fondamental réduit le premier Accord do - mi - sol, dont la Fondamentale est do.
La Fondamentale d'un Son musical est la Fréquence la plus basse (f) dans la Décomposition d'une onde périodique en séries de Fourier.
Voir Sonagramme.
La Forme musicale en tant que Genre musical désigne une catégorie d'Oeuvre musicale : Concerto, Fantaisie, Prélude, Symphonie, etc.
La Forme musicale en tant que Structure musicale est un enchaînement de Phrases musicales de longueur identique, pouvant être parfois répétées.
Les différentes Phrases sont nommées par des lettres : A, B, C, etc.
Les Phrases quasi identiques, n'ayant souvent que quelques Notes de différence en fin de Phrase, sont nommées en ajoutant un prime à la lettre désignant la Phrase originale. Exemple : A et A'
Exemples de Forme musicale : Anatole en musique Jazz/Rock (A A B A), Aria da capo (A B A'), Chanson de Noël (A A B A), Lied (A B A'), Menuet ou Scherzo (A A B B), Rondo ou Rondeau (A B A C A D A), Sonate (A A B A'), Strophique (A A A), Thème et variations (A A' A").
La Fréquence est le nombre de Périodes par seconde (en Hertz ou seconde-1).
Si f est la Fréquence et T la Période, alors : f = 1/T.
La Gamme est une succession de Notes Conjointes selon une échelle relevant de l'esthétique musicale, la dernière Note répétant la première à l'Octave supérieure si la Gamme est ascendante, ou inférieure si la Gamme est descendante.

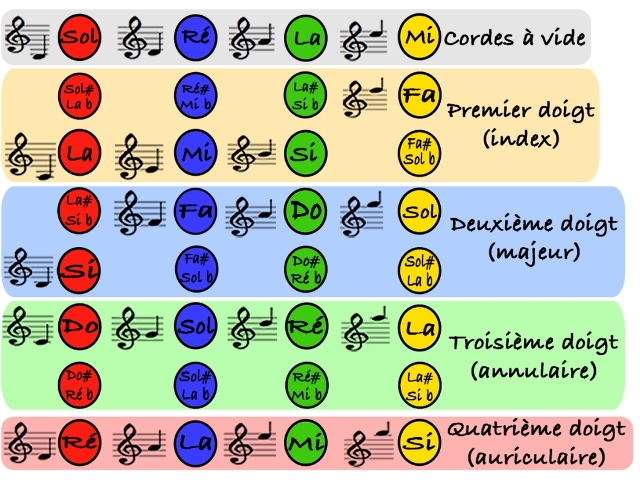
La Gamme chromatique est la Gamme qui divise l'Octave en 12 Demi-tons.
Selon les Instruments, les Demi-tons ne sont pas nécessairement tous égaux (Demi-ton chromatique et Demi-ton diatonique).
- Au piano (voir Figure 1 ci-dessus), la Gamme comprend 12 Notes différentes : les 7 touches blanches (Notes de la Gamme diatonique) et les 5 touches noires intercalées (leurs Altérations).
- Au violon (voir Figure 2 ci-dessus), la Gamme comprend usuellement 17 Notes différentes : 7 Notes naturelles, 5 Altérations en Dièse (do#, ré#, fa#, sol#, la#) et 5 Altérations en Bémol (réb, mib, solb, lab, sib). Ainsi, entre les Notes do et ré se trouvent deux Notes intermédiaires : réb et, un Comma plus haut, do#. A noter que les 4 autres Altérations possibles (fab, mi#, si#, dob), bien que réalisables au violon, sont très peu utilisés.
Voir Gamme de Pythagore.
Voir Gamme de Zarlino.
La Gamme diatonique est la Gamme qui divise l'Octave en 7 Intervalles dont 5 valant un Ton et 2 valant un Demi-ton, les deux Demi-tons étant toujours séparés par deux ou trois Tons.
Il existe essentiellement trois Gammes diatoniques : la Gamme de Zarlino, la Gamme de Pythagore et la Gamme tempérée.
Le Tableau ci-dessous compare ces trois Gammes diatoniques, en Mode Majeur, selon leurs Intervalles respectifs donnés par le rapport de Fréquences entre deux Notes Conjointes.
- La Gamme de Zarlino est utilisée lorsqu'un groupe vocal (choristes) ou un groupe de violonistes interprète une musique polyphonique Consonante et souhaite provoquer au niveau des auditeurs une sensation de perfection que l'on n'a pas avec un Instrument accordé en Gamme tempérée.
- La Gamme de Pythagore est utilisée sur les Instruments que l'on accorde par Quintes (violon par exemple) ou par Quartes (contrebasse par exemple). Elle permet également à certains solistes (violoniste, chanteur, etc.) de jouer naturellement une Ligne mélodique plus expressive, la Tierce majeure étant plus haute que dans les autres Gammes usuelles (voir Tableau ci-dessous).
- La Gamme tempérée est largement utilisée en musique occidentale (voir détails).
| Notes | do | ré | mi | fa | sol | la | si | do | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intervalles en Mode Majeur | Ton | Ton | 1/2 Ton | Ton | Ton | Ton | 1/2 Ton | ||||||||
| Gamme de Zarlino | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||
| Gamme de Pythagore | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | ||||||||
| Gamme tempérée | 22/12 | 22/12 | 21/12 | 22/12 | 22/12 | 22/12 | 21/12 |
Il existe de nombreuses Gammes dites "exotiques" en musique occidentale.
Le Tableau ci-dessous en donne quelques-unes qui divisent l'Octave en 7 Intervalles.
| Degrés | I | II | III | IV | V | VI | VII | VIII | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mode Nahawand (Arabo-turc) ou Mineur harmonique | Ton | 1/2 Ton | Ton | Ton | 1/2 Ton | 3/2 Ton | 1/2 Ton | ||||||||
| Mode Nawa atar (Arabo-turc) ou Tzigane ou Hongrois | Ton | 1/2 Ton | 3/2 Ton | 1/2 Ton | 1/2 Ton | 3/2 Ton | 1/2 Ton | ||||||||
| Mode Oriental | 1/2 Ton | 3/2 Ton | 1/2 Ton | Ton | 1/2 Ton | 3/2 Ton | 1/2 Ton | ||||||||
| Mode Andalou | 1/2 Ton | 3/2 Ton | 1/2 Ton | Ton | 1/2 Ton | Ton | Ton | ||||||||
| Mode Balkan | 1/2 Ton | Ton | Ton | Ton | 1/2 Ton | 3/2 Ton | 1/2 Ton | ||||||||
| Mode Bhairava (Inde du Nord) | 1/2 Ton | Ton | Ton | Ton | 1/2 Ton | Ton | Ton | ||||||||
| Mode Vaschaspati (Inde) ou Bartok ou Acoustique | Ton | Ton | Ton | 1/2 Ton | Ton | 1/2 Ton | Ton |
La Gamme tempérée est la Gamme qui divise l'Octave en Intervalles égaux, sans se préoccuper de la Consonance entre les Notes ainsi déterminées.
Le découpage le plus répandu contient 12 Intervalles (Demi-tons) qui ont chacun une largeur de 1/12 Octave correspondant à un rapport de Fréquences entre deux Notes Conjointes de 1,05946 = 21/12.
La Gamme tempérée, dont la paternité est généralement attribuée au musicien Andreas Werckmeister en 1691, est largement utilisée en musique occidentale depuis le 18e siècle. J.S. Bach fut l'un des premiers musiciens à l'adopter (cf "Le Clavier bien tempéré", recueil d'oeuvres écrites de 1722 à 1744).
Bien que difficile à accorder et au prix de n'avoir plus aucun Intervalle "juste" au sens de Zarlino ou de Pythagore, elle présente toutefois de nombreux avantages (uniformisation des Demi-tons, Transpositions et Modulations à l'infini, etc.).
La Gamme est tempérée sur la plupart des Instruments à clavier (piano, orgue, clavecin, harmonium, accordéon, etc.), sur certains Instruments à cordes (guitare, mandoline, luth, harpe, viole, etc.) et sur les Instruments à vent avec clés ou pistons (trompette, tuba, clarinette, hautbois, etc.).
Calcul de la Fréquence d'une Note en Gamme tempérée : ftemp en Herz = 440 x 2n/12
avec : n = nombre de Demi-tons (nombre positif ou négatif) séparant la Note du Diapason (la3).
Exemples : do4 = 440 x 23/12 = 523,25 Hz ; ré3 = 440 x 2-7/12 = 293,66 Hz
Voir Forme musicale.
Voir Liaison.
Dans la théorie de la musique occidentale, l'Harmonie classique ou tonale (souvent appelée Harmonie) étudie la construction des Accords (Notes et/ou Instruments simultanés) et leurs Enchaînements (mélodie).
L'Harmonie a remplacé progressivement le Contrepoint à partir du milieu du 18e siècle.
Pour la plupart des musiciens, l'Harmonie est la combinaison Dissonante de Notes, pleines de tensions, qui se résolvent miraculeusement en un Accord Consonant.
Pour le compositeur américain Lejaren Hiller, "la musique est un compromis entre la monotonie et le chaos".
Pour l'Auteur, l'harmonie serait l'alternance entre deux intérêts (ou plaisirs) à la fois complémentaires et antagonistes :
- d'une part, la perception d'Intervalles et d'Accords déjà présents à l'état pur dans les six premiers Harmoniques de chaque Son musical (essentiellement l'Octave, la Quinte, la Quarte, la Sixte majeure et l'Accord parfait majeur), donnant une impression de satisfaction, voire d'attente comblée,
- d'autre part, la perception d'autres motifs sonores donnant un sentiment de nouveauté, voire d'imprévu, par rapport aux motifs habituels.
Cette alternance entre habitude et nouveauté, tout en évitant soigneusement la saturation donnant un sentiment de monotonie, voire de lassitude, dépendrait largement des origines culturelles du compositeur et de l'éducation de son oreille musicale.
Les Règles d'Harmonie sont regroupées en plusieurs catégories :
- Règles horizontales (Tessiture, Tonalité, Intervalle mélodique, Fonction tonale) ;
- Règles verticales (Accord au repos, Doublure, Renversement, Ecartement entre voix, Contrepoint) ;
- Règles d'enchaînement (Mouvement, Enchaînement) ;
- Règles de sémantique musicale (lois psychoacoustiques de la perception musicale).
Les Harmoniques ou Partiels (de rang n) sont les Fréquences nf (2f, 3f, 4f, etc.) qui sont des multiples entiers de la Fondamentale (f) dans la Décomposition d'une onde périodique en séries de Fourier.
Par extension, on nomme "Harmonique de rang 1" la Fondamentale f et "Harmoniques" l'ensemble complet de la Fondamentale et des Harmoniques supérieurs.




En Musique tonale, l'Harmonisation consiste, pour une Mélodie existante, à rajouter des Accords ou d'autres Mélodies conformément aux Règles de l'Harmonie.
Exemple d'Harmonisation : l'écriture d'un Accord de trois notes à quatre Voix.
Autre exemple d'Harmonisation : l'Harmonisation des Gammes diatoniques par les Accords.
Pour illustrer la méthode, prenons l'exemple de la Gamme de mi Bémol majeur à Harmoniser par des Accords de trois notes :
Etape 1 : Construction de la Gamme (voir Figure 1 ci-dessus)
Conformément au Tableau des Armures, on voit que cette Gamme possède 3 Bémols à la Clef : si, mi et la. On la construit donc en prenant en compte ces Altérations.
Etape 2 : Construction des Accords (voir Figure 2 ci-dessus)
On construit, sur chaque Note de cette Gamme, un Accord de trois notes à l'Etat classé (i.e. en empilant les Tierces), et sans s'occuper de l'Altération des Notes rajoutées.
Etape 3 : Respect des Altérations constitutives inhérentes aux Gammes Majeure et Mineure naturelle (voir Figure 3 ci-dessus)
On Altère les Notes rajoutées conformément aux Altérations de l'Armure, c'est-à-dire en bémolisant les Notes si, mi et la.
Etape 4 : Respect des Altérations accidentelles inhérentes aux Gammes Mineure harmonique ou Mineure mélodique ascendant (voir Figure 4 ci-dessus)
On Altère toutes les Notes des Accords conformément aux Altérations accidentelles de la Gamme Mineure, c'est-à-dire en haussant d'un Demi-ton le Degré VI en Gamme Mineure mélodique ascendant et aussi le Degré VII en Gammes Mineure harmonique et Mineure mélodique ascendant (cf [FAB Unité 7]).
L'exemple de la Gamme de mi Bémol majeur n'est pas concerné par l'étape 4. Voyons le résultat de cette étape sur les deux exemples suivants :
- Harmonisation de la Gamme de do mineur harmonique par des Accords de trois notes (voir Figure 2 de cette Gamme) : toutes les Notes sib de la Gamme de do mineur naturel se trouvent ainsi modifiées en si Bécarre.
- Harmonisation de la Gamme de la mineur mélodique par des Accords de cinq notes (cf [Gui, Degrés harmonisés à cinq voix, Figure 4]) : toutes les Notes fa et sol de la Gamme de la mineur naturel se trouvent ainsi modifiées en fa# et sol#.
Cette méthode assure que la Structure des Accords obtenus ne change jamais quand on change le Nom de la Gamme.
Ainsi, pour l'Harmonisation des Gammes majeures par des Accords de trois notes par exemple, la série des 7 Accords obtenus sera toujours de type : M m m M M m dim, que l'on soit en mi Bémol majeur ou en do majeur.
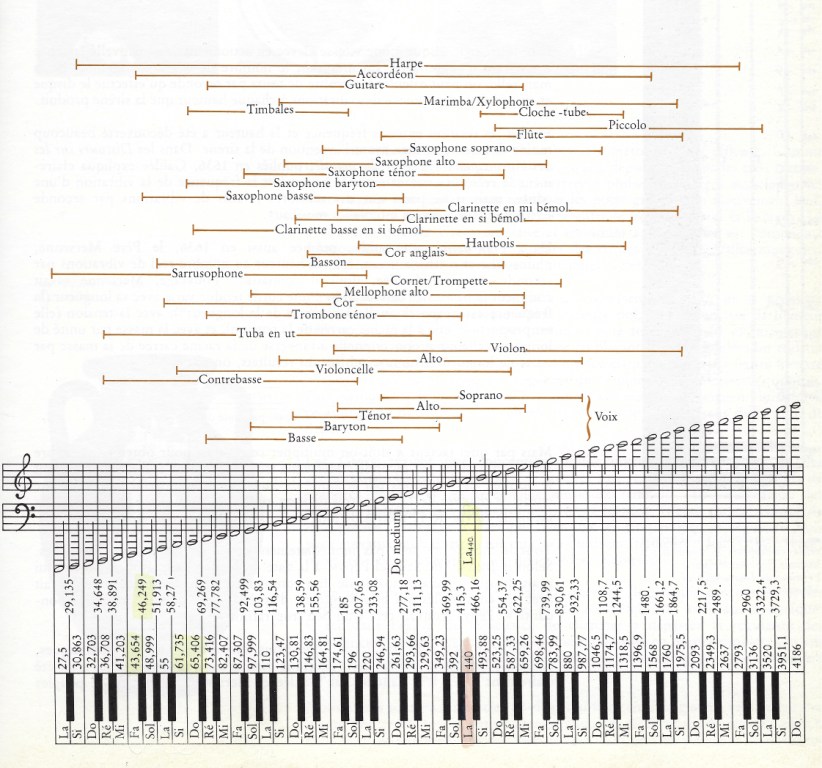
La Hauteur d'un Son musical est la Fréquence de sa Fondamentale.
La Figure ci-dessus montre la Fréquence des différentes Notes d'un clavier de piano, ainsi que la Tessiture (ou Registres) de plusieurs autres Instruments de musique.
En notation musicale, la Hauteur d'une Note est définie par deux caractéristiques :
- la position verticale de la tête de la Figure de Note sur la Portée,
- la Clef en début de Portée.







Un Instrument de musique est un objet pouvant produire un Son contrôlé par un musicien. Par extension, un Instrument de musique peut être également la voix chantée, les mains ou les pieds du musicien.
Un Instrument de musique se divise en deux parties distinctes : le Vibrateur qui produit la vibration (Corde vibrante, colonne d'air vibrante contenue dans un Tuyau sonore, Membrane vibrante, autres procédés de percussion, électronique) et la Caisse de résonance qui transforme cette vibration en un Timbre caractéristique de l'Instrument.
Les Instruments de musique sont classés conventionnellement par leur méthode de production du Son, quel que soit leur matériau. Ainsi, une clarinette en métal ou un saxophone en cuivre sont classés comme "Instruments à bois". Les différentes méthodes sont les suivantes (voir Figures ci-dessus) :
Instruments à cordes (production du son par Corde vibrante) :
- à cordes frottées (alto, contrebasse, trompette marine, vielle à roue, viole de gambe, violon, violoncelle, etc.),
- à cordes pincées à l'aide des doigts (banjo, cithare, contrebassine, guitare, harpe, luth, lyre, mandoline, etc.),
- à cordes pincées à l'aide d'un clavier (clavecin, épinette, virginale, etc.),
- à cordes frappées (clavicorde, cymbalum, piano, tympanon, etc.).
Instruments à vent (production du son par colonne d'air vibrante contenue dans un Tuyau sonore) :
- les Voix (chantées),
- les Bois, qui comportent un biseau ou une anche :
- à biseau (flûte à bec, flûte de pan, flûte traversière, orgue à bouche, etc.),
- à anche libre (accordéon, harmonica, harmonium, orgue à anche, etc.),
- à anche simple (clarinette, saxophone, etc.),
- à anche double (basson, bombarde, contrebasson, cor anglais, cornemuse, hautbois, etc.),
- les Cuivres, pour lesquels la vibration des lèvres du musicien dans une embouchure fait office de anche lippale (clairon, cor d'harmonie, cor naturel, corne, cornet à pistons, didgeridoo, saxhorn, serpent, trombone, trompe de chasse, trompette, tuba, etc.).
Instruments de percussion (production du son par Membrane vibrante, Plaque vibrante ou autre procédé) :
- les peaux, qui comporte une Membrane frappée par les mains ou par des baguettes (bongo, djembé, caisse claire, grosse caisse, tambour, tambourin, timbale, tom, etc.),
- les claviers, qui comportent une série de lames frappées par des baguettes ou par un clavier (célesta, marimba, steel-drum, tongue drum, vibraphone, xylophone, etc.),
- les autres percussions (appelées accessoires), qui ne produisent généralement qu'un seul son (castagnettes, clave, cloche, crécelle, cymbale, gong, grelots, hochet, maracas, triangle, etc.),
- la batterie, qui associe plusieurs instruments de percussion dont caisse claire, grosse caisse, cymbales et toms.
Instruments de combinaison qui associent plusieurs modes de mise en vibration :
- les orgues combinant tuyaux à bouche et tuyaux à anche,
- les Instruments mécaniques (limonaire, orgue de Barbarie, serinette, etc.),
- le claviorganum, combinant orgue et clavecin actionnés par les mêmes claviers,
- la "Marble Machine", créé par le groupe Wintergatan, combinant guitare basse, vibraphone, cymbales et diverses percussions.
Instruments électriques :
- les Instruments électromécaniques (orgue Hammond, Yamaha CP80, etc.),
- les Instruments électroniques (guitare électrique, instrument virtuel (ordinateur), ondes musicales Martenot, piano numérique, synthétiseurs, thérémine, vent électronique, etc.).
Sur une partition d'orchestre, les Instruments sont conventionnellement regroupés par Familles ou Groupes, de haut en bas : Bois, Cors, Cuivres, Percussions, Claviers (piano, clavecin, orgue), Voix (chantées) et Cordes.
Dans chaque Famille, les Instruments sont placés de haut en bas depuis l'aigu jusqu'au grave.
Au niveau acoustique, chaque type d'Instrument a sa signature acoustique sous forme de Sonagramme.
Au niveau musical, chaque type d'Instrument a sa méthode d'Accordage et son propre Jeu de Notes.
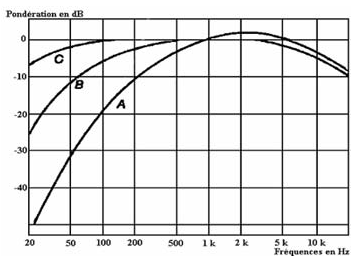
L'Intensité physiologique globale d'un Son musical est une notion complexe obtenue en reportant le Spectre sonore sur les courbes isosoniques du Son pur.
Pour simplifier cette complexité, on préfère utiliser des courbes d'affaiblissement indépendantes des Intensités physiques du Spectre sonore (voir Figure ci-dessus, avec courbes A, B et C correspondant respectivement aux Sons d'Intensité faible, moyenne et forte). Les Intensités physiques sont ainsi pondérées avec les affaiblissements définis par la courbe A qui est la plus utilisée.
Exemple de calcul pour un Bruit (cf [PUJ Notions]) :
Le Tableau ci-dessous donne, pour chaque bande de Fréquences d'Octave, le Niveau d'Intensité (mesuré), le niveau d'affaiblissement (issu de la courbe A en Figure ci-dessus), le Niveau d'Intensité pondérée S et l'Intensité physique pondérée I (issue de la formule : S = 10 log10(I/I0)).
En faisant la somme de ces Intensités physiques pondérées, on trouve : I global = 9,2 107 I0, ce qui donne un Niveau d'Intensité pondérée globale (ou Intensité physiologique globale) : S global = 79,6 dB
| Fréquence (Hz) | Niveau d'Intensité (dB) | Niveau d'affaiblissement (dB) | Niveau d'Intensité pondérée (dB) | Intensité physique pondérée (W/m2) |
|---|---|---|---|---|
| 31,5 | 89,4 | -39 | 50 | 105 I0 |
| 63 | 86,2 | -26 | 60 | 106 I0 |
| 125 | 86,1 | -16 | 70 | 107 I0 |
| 250 | 78,6 | -8 | 70 | 107 I0 |
| 500 | 76,2 | -3 | 73 | 2 107 I0 |
| 1000 | 73,0 | 0 | 73 | 2 107 I0 |
| 2000 | 71,8 | +1 | 73 | 2 107 I0 |
| 4000 | 69,0 | +1 | 70 | 107 I0 |
| 8000 | 61,1 | -1 | 60 | 106 I0 |
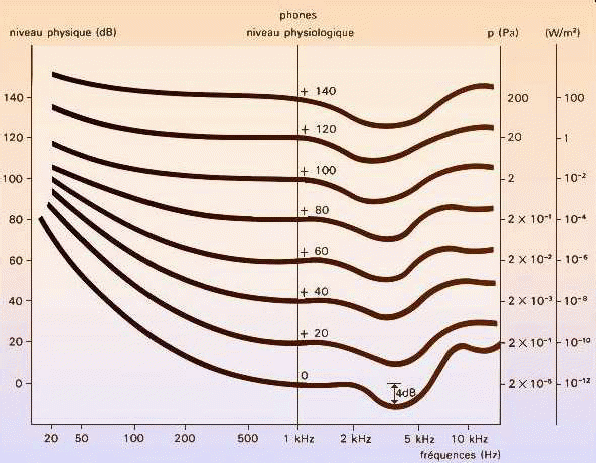
Il existe trois sortes d'Intensité pour un Son pur (cf [MAT Perception][PUJ Notions]) :
- L'Intensité physique (I) qui est liée à l'amplitude A de la pression acoustique p(t) du Son par la relation suivante :
I = A2/(ρ c)
avec I en W/m2, A en Pa, ρ en kg/m3 (masse volumique de l'air) et c en m/s (vitesse du son).
Pour l'air à 20°C et à la pression atmosphérique, on a : ρ c = 412 N.s.m-3
I0 = 10-12 W/m2 correspond au seuil d'audibilité.
- Le Niveau d'intensité ou niveau de pression acoustique (S) qui est ressenti par une oreille idéale (sans distorsions liées à la Hauteur du Son) et qui vaut :
S = 10 log10(I/I0) = 20 log10(A/A0)
avec S en dB et A0 = 2 10-5 Pa
A0 est la plus faible pression acoustique à laquelle l'oreille est sensible (correspondant au seuil d'audibilité I0).
Les Sons audibles s'étagent de 0 dB (seuil d'audibilité) à 140 dB, le seuil de douleur valant 120 dB.
- L'Intensité physiologique qui est ressenti par une oreille normale (en fonction du Niveau d'intensité et de la Fréquence, selon des courbes isosoniques (voir Figure ci-dessus)).
Exemple (voir Figure ci-dessus) : Pour un même Niveau d'Intensité 40 dB, un Son à 1000 Hz a une Intensité physiologique de 40 dB alors qu'un un Son à 100 Hz a une Intensité physiologique de 3 dB (proche du seuil d'audibilité).
A noter (cf [MAT Perception]) : Ces courbes montrent que, lorsqu'on diminue le niveau moyen d'une écoute, on comprime beaucoup plus fortement les Fréquences graves que les autres.
Ainsi, un concert d'orchestre sera d'abord dépouillé de toute vigueur puis, peu à peu, de tous ses Instruments à graves dominantes, notamment les Instruments à percussion. Le concert se transforme alors en orchestre de chambre.

L'Intervalle harmonique est l'ensemble de deux Sons entendus simultanément.
L'Intervalle se mesure par le rapport de leurs Fréquences ou par une largeur exprimée en portion d'Octave. Exemple : pour une Quinte, l'Intervalle est de 3/2 correspondant à une largeur de 0,58 Octave (log2(3/2)).
En musique occidentale (voir Figure ci-dessus), l'Intervalle est caractérisé par :
- un Nom correspondant au nombre de Notes Conjointes englobées ou, autrement dit, au nombre de Degrés consécutifs de la Gamme diatonique qui sont englobés (exemple : "Tierce" pour l'Intervalle do - mi ou do - mib),
- un Qualificatif donnant l'étendue de l'Intervalle compte tenu des Tons et Demi-tons diatoniques (exemple : Tierce "majeure" pour une étendue de 2 Tons).
Le Tableau ci-dessous donne la liste des Intervalles usuels (en gras : les Intervalles de référence de la Gamme de do majeur).
Rappel : 1 Ton = 1 Demi-ton chromatique + 1 Demi-ton diatonique.
| Nom et Qualificatif | Contenu en Tons et Demi-tons diatoniques | Exemples | Rapport des Fréquences par-rapport au do selon Gamme de Zarlino | Rapport des Fréquences selon Gamme de Pythagore |
|---|---|---|---|---|
| Ton | 10/9 (Ton mineur) ; 9/8 (Ton majeur) | 9/8 = Epogdoon | ||
| Demi-ton chromatique | 25/24 (petit chromate) ; 135/128 (grand chromate) | 37/211 = 2187/2048 = Apotome | ||
| Demi-ton diatonique | 16/15 (petit diaton) ; 27/25 (grand diaton) | 28/35 = 256/243 = Limma | ||
| Comma | 81/80 (comma syntonique) | 312/219 | ||
| Prime diminuée ou Unisson diminué | -1 Ton et 1 Demi-ton ( = -1 Demi-ton chromatique) | do - dob | 24/25 | 211/37 |
| 1. Prime juste ou Unisson juste | 0 Ton et 0 Demi-ton | do - do | 1/1 | 1/1 |
| Prime augmentée ou Unisson augmenté | 0 Ton et 1 Demi-ton chromatique | do - do# | 25/24 | 37/211 |
| Seconde diminuée | -1 Ton et 2 Demi-tons ( = 1 Demi-ton diatonique - 1 Demi-ton chromatique) | do - rébb | 219/312 | |
| Seconde mineure | 0 Ton et 1 Demi-ton | do - réb ; mi - fa ; sol# - la | 16/15 | 28/35 |
| 2. Seconde majeure | 1 Ton | do - ré | 9/8 | 9/8 |
| Seconde augmentée | 1 Ton et 1 Demi-ton chromatique | do - ré# ; fa - sol# | 75/64 | 39/214 |
| Tierce diminuée | 0 Ton et 2 Demi-tons | do - mibb ; do# - mib | 216/310 | |
| Tierce mineure | 1 Ton et 1 Demi-ton | do - mib ; mi - sol | 6/5 | 25/33 |
| 3. Tierce majeure | 2 Tons | do - mi ; si - ré# | 5/4 | 81/64 |
| Tierce augmentée | 2 Tons et 1 Demi-ton chromatique | do - mi# | 125/96 | 311/217 |
| Quarte diminuée | 1 Ton et 2 Demi-tons | do - fab ; do# - fa | 32/25 | 213/38 |
| 4. Quarte juste | 2 Tons et 1 Demi-ton | do - fa ; mib - lab | 4/3 | 4/3 |
| Quarte augmentée ou Triton | 3 Tons | do - fa# ; fa - si | 45/32 | 729/512 |
| Quinte diminuée (ou Triton en Gamme tempérée) | 2 Tons et 2 Demi-tons | do - solb | 36/25 | 210/36 |
| 5. Quinte juste | 3 Tons et 1 Demi-ton | do - sol | 3/2 | 3/2 |
| Quinte augmentée | 4 Tons | do - sol# | 25/16 | 38/212 |
| Sixte diminuée | 2 Tons et 3 Demi-tons | do - labb | 218/311 | |
| Sixte mineure | 3 Tons et 2 Demi-tons | do - lab ; mi - do | 8/5 | 27/34 |
| 6. Sixte majeure | 4 Tons et 1 Demi-ton | do - la ; mib - do | 5/3 | 27/16 |
| Sixte augmentée | 5 Tons | do - la# | 225/128 | 310/215 |
| Septième diminuée | 3 Tons et 3 Demi-tons | do - sibb ; do# - sib | 215/39 | |
| Septième mineure | 4 Tons et 2 Demi-tons | do - sib | 9/5 | 24/32 |
| 7. Septième majeure | 5 Tons et 1 Demi-ton | do - si | 15/8 | 243/128 |
| Septième augmentée | 6 Tons | do - si# | 125/64 | 312/218 |
| Octave diminuée | 4 Tons et 3 Demi-tons | do - dob à l'Octave | 48/25 | 212/37 |
| 8. Octave juste | 5 Tons et 2 Demi-tons | do - do à l'Octave | 2/1 | 2/1 |
| Octave augmentée | 6 Tons et 1 Demi-ton | do - do# à l'Octave | 37/210 | |
| Neuvième diminuée | 4 Tons et 4 Demi-tons | do - rébb à l'Octave | 220/312 | |
| Neuvième mineure | 5 Tons et 3 Demi-tons | do - réb à l'Octave | ||
| 9. Neuvième majeure | 6 Tons et 2 Demi-tons | do - ré à l'Octave | ||
| Neuvième augmentée | 7 Tons et 1 Demi-ton | do - ré# à l'Octave | ||
| Dixième diminuée | 5 Tons et 4 Demi-tons | do - mibb à l'Octave | ||
| Dixième mineure | 6 Tons et 3 Demi-tons | do - mib à l'Octave | ||
| 10. Dixième majeure | 7 Tons et 2 Demi-tons | do - mi à l'Octave | ||
| Dixième augmentée | 8 Tons et 1 Demi-ton | do - mi# à l'Octave | ||
| Onzième diminuée | 6 Tons et 4 Demi-tons | do - fab à l'Octave | ||
| 11. Onzième juste | 7 Tons et 3 Demi-tons | do - fa à l'Octave | ||
| Onzième augmentée | 8 Tons et 2 Demi-tons | do - fa# à l'Octave | ||
| Douzième diminuée | 7 Tons et 4 Demi-tons | do - solb à l'Octave | ||
| 12. Douzième juste | 8 Tons et 3 Demi-tons | do - sol à l'Octave | ||
| Douzième augmentée | 9 Tons et 2 Demi-tons | do - sol# à l'Octave | ||
| Treizième diminuée | 7 Tons et 5 Demi-tons | do - labb à l'Octave | ||
| Treizième mineure | 8 Tons et 4 Demi-tons | do - lab à l'Octave | ||
| 13. Treizième majeure | 9 Tons et 3 Demi-tons | do - la à l'Octave | ||
| Treizième augmentée | 10 Tons et 2 Demi-tons | do - la# à l'Octave | ||
| Quatorzième diminuée | 8 Tons et 5 Demi-tons | do - sibb à l'Octave | ||
| Quatorzième mineure | 9 Tons et 4 Demi-tons | do - sib à l'Octave | ||
| 14. Quatorzième majeure | 10 Tons et 3 Demi-tons | do - si à l'Octave | ||
| Double octave diminuée | 11 Tons et 1 Demi-ton | do - dob à l'Octave | ||
| Quatorzième augmentée | 11 Tons et 2 Demi-tons | do - si# à l'Octave | ||
| 15. Double octave juste | 10 Tons et 4 Demi-tons | do - do à l'Octave double |
L'Intervalle mélodique est l'ensemble de deux Sons entendus successivement.
Un Intervalle pur (ou Intervalle naturel) est un Intervalle dont le rapport des Fréquences est une fraction simple de deux nombres entiers, c'est-à-dire de la forme (n + 1)/n, avec n > 0.
On peut citer (voir Intervalle harmonique) : Seconde mineure (16/15), Seconde majeure (9/8), Tierce mineure (6/5), Tierce majeure (5/4), Quarte juste (4/3), Quinte juste (3/2), Octave juste (2/1).
Attention : le terme "Intervalle pur" s'emploie aussi pour désigner une fraction quelconque de deux nombres entiers (exemple : Sixte majeure (5/3)).
Les Instruments à clavier n'ont plus qu'un seul Intervalle pur, l'Octave de rapport 2/1.
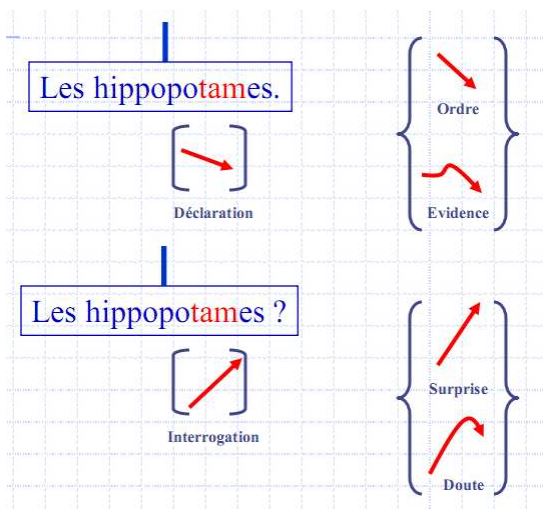
L'Intonation est un des composants de la Prosodie qui permet au locuteur de décliner une Phrase sous forme déclarative ou interrogative par variation de la Fréquence Fondamentale F0 de ses cordes vocales.
En français, l'Intonation est toujours placée sur la dernière Syllabe accentuée (portant l'Accent tonique) de la Phrase et se décline principalement selon les deux modalités suivantes et leurs variantes (cf [MARTIN, Ponctuation, p.101] [MARTIN, Intonation, p.151] [MARTIN, Enseignement]) :
Modalité déclarative :
- Assertion : intonation descendante (exemple : Tu viens.)
- Injonction ou ordre : intonation descendante abruptement (exemple : Tu viens !)
- Evidence : intonation montante courte puis descendante (exemple : Tu viens...)
Modalité interrogative :
- Question : intonation montante (exemple : Tu viens ?)
- Surprise ou exclamation : intonation montante abruptement (exemple : Tu viens !!)
- Doute : intonation montante puis descendante courte (exemple : Tu viens !?)
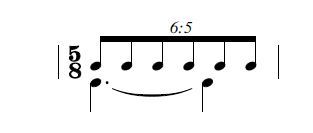

Un Rythme est irrationnel lorsque ses divisions diffèrent du Nombre de Temps de la Mesure qui les accueille.
Chaque division irrationnelle porte un nom : Duolet (2), Triolet (3), Quartolet (4), Quintolet (5), Sextolet (6), Septolet (7), Octolet (8), Nonolet (9), Décalet (10), Undécalet (11), Dodécalet (12).
Une telle figure rythmique irrégulière est symbolisée par une fraction (A:B) écrite au-dessus ou au-dessous des Notes à qui elle est attribuée, le dénominateur (B) de la fraction étant parfois sous-entendu (par exemple 3 au lieu de 3:2 pour un Triolet).
La Figure 1 ci-dessus montre un Sextolet de Croches pour lequel on doit jouer six Croches pendant le temps de cinq (notation = "6:5").
Cette notation s'applique également aux Silences (voir Figure 2 ci-dessus).
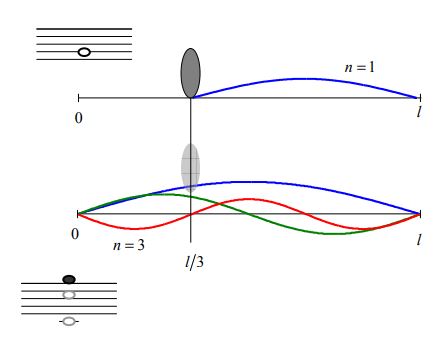
Chaque Instrument de musique possède son propre jeu au niveau de l'exécution des Notes par le musicien.
Instrument à cordes (production du son par Corde vibrante) :
- Pour les Instruments à cordes frappées (exemple du piano), le musicien exécute la Gamme en enfonçant les touches d'un clavier. Chaque touche commande un marteau recouvert de feutre qui vient frapper un groupe correspondant de deux ou trois cordes. Au même instant, le petit bloc de feutre doux appelé étouffoir, qui au repos est au contact des cordes, se soulève pour leur permettre de vibrer librement. Quand on lâche la touche, l'étouffoir retombe et arrête la vibration (cf [WEIN]). Le musicien peut également donner de la Brillance et de la puissance au Son en relevant complètement les étouffoirs au moyen des pédales (cf [BOU Propagation]).
Au piano, le Registre va du la1 au la6 avec 85 Notes (12 touches par Octave) et 225 cordes.
- Pour les Instruments à cordes pincées (exemple de la guitare) ou frottées (exemple du violon), le musicien a deux possibilités pour exécuter la Gamme :
- En pressant la corde contre la barre de touche, il supprime la vibration dans toute la partie de la corde comprise entre le doigt et le sillet de tête. La corde est raccourcie et sa nouvelle longueur détermine la Hauteur de la Note (voir Gamme chromatique).
- En effleurant la corde au lieu de la presser, le musicien peut produire les Fréquences Harmoniques supérieures donnant une sonorité "flûtée" : à la moitié de la longueur pour l'Harmonique de rang 2 (produisant l'Octave du Son fondamental), au tiers pour l'Harmonique de rang 3 (produisant la Quinte au-dessus de l'Octave), au quart pour l'Harmonique de rang 4 (produisant le double Octave), etc.
Pour les Harmoniques dits "naturels", le Son fondamental est produit par la corde à vide et le doigt effleure alors la corde à la moitié, au tiers, au quart, etc., de sa longueur pour produire les Sons 2, 3, 4, etc (cf [LAROUSSE]). Sur une partition, la Note entendue est, soit surmontée d'un zéro, soit remplacée par un losange surmonté de l'indication "H." ou "Harm." (cf [TOS, p.21]).
Pour les Harmoniques dits "artificiels", le Son fondamental est produit par l'index qui appuie sur la corde, tandis qu'un autre doigt effleure la corde à intervalle de Quarte pour obtenir le Son 4 ou à intervalle de Quinte pour obtenir le Son 5 (cf [LAROUSSE]). Sur une partition, la Note entendue est remplacée par un losange surmonté de l'indication "H.A." (cf [TOS, p.21]).
- Pour produire la Note, il reste ensuite à pincer la corde (guitare) ou à la frotter avec l'archet (violon).
- Sur un violon par exemple, une Corde pressée au 1/3 de sa longueur L produit le Son fondamental d'une corde de longueur 2L/3 selon la Fréquence f = (1/2) (n = 1) c/(2L/3) = (3/4) c/L (voir Figure ci-dessus, partie haute). En effleurant la corde de longueur L au même endroit, le Son fondamental est étouffé ainsi que l'Harmonique 2 (voir Figure ci-dessus, partie basse). En revanche, l'Harmonique 3 qui présente un noeud à cet endroit n'est pratiquement pas atténué. La Fréquence f = (1/2) (n = 3) c/L = (3/2) c/L est entendue et on gagne une Octave par rapport à la Fréquence d'une corde pressée au même endroit (cf [PASC, p.10]).
Dans la Famille des violons, les Sons Fondamentaux (corde à vide) en fonction de la longueur des cordes sont les suivants (cf [BOU Propagation]) :
Violon (33 cm) : mi4 la3 ré3 sol2
Alto (35 cm) : la3 ré3 sol2 do2
Violoncelle (70 cm) : la2 ré2 sol1 do1
Contrebasse (100 cm) : sol1 ré1 la0 mi0
Pour la guitare qui comporte 6 cordes, les Sons Fondamentaux sont les suivants : mi1 la1 ré2 sol2 si2 mi3.
Contrairement au pianiste, le violoniste a beaucoup de possibilités dans son jeu : le démanché (plus aigu), le Vibrato, les Trilles, le jeu des Harmoniques (voir texte ci-dessus), le jeu sur deux cordes, le pizz (jeu sur une corde pincée), le Glissando (cf [BOU Propagation]).
Instrument à vent (production du son par colonne d'air vibrante contenue dans un Tuyau sonore) :
Mécanisme général :
Dans un Tuyau sonore, l'air insufflé à son embouchure passe à travers une soupape et produit des vibrations de la colonne d'air contenue dans le tuyau. La soupape peut être à flux d'air commandé en pression (anche ou lèvres vibrantes du musicien) ou commandé en vitesse (biseau). La soupape transforme alors le flux d'air permanent en séries de bouffées à la Fréquence imposée par le tuyau et les éventuels trous latéraux (cf [BENA, Les bois]).
La Hauteur du son émis dépend essentiellement de la longueur du tuyau (comme pour les orgues), des ouvertures éventuelles présentes dans le corps de l'Instrument (comme pour les flûtes) et des conditions d'ouverture et de fermeture du tuyau aux extrémités.
Dans l'exemple de la trompette, quand le musicien souffle dans son Instrument, un régime d'oscillation forcée s'établit, dans lequel plusieurs Fréquences de Résonance de la colonne d'air coopèrent avec les oscillations des lèvres pour fournir de l'énergie sous forme d'une oscillation régulière correspondant à la Fréquence désirée. Le musicien ajuste ainsi la tension de ses lèvres de manière à ce que leur Fréquence de vibration naturelle favorise l'oscillation de la colonne d'air à la Note voulue (cf [BENA, Les cuivres]).
Ce résultat peut être généralisé à tous les Instruments à vent, dont les cuivres (cf [BENA, Les cuivres]).
Le musicien a alors deux possibilités pour exécuter la Gamme.
La première consiste à souffler de plus en plus fort dans le tuyau. Le musicien obtient alors une série discrète de Sons partiels dont la Fréquence correspond approximativement à la suite des Harmoniques du tuyau entier. Ces partiels sont des Sons Fondamentaux nouveaux, accompagnés chacun de sa propre série d'Harmoniques, et correspondent aux Modes de propagation de la colonne d'air (cf [GAB Acoustique] [BENA Les bois]).
La seconde possibilité consiste à modifier les dimensions du tuyau comme suit :
- Pour les Bois (exemples de la flûte ou de la clarinette), le musicien exécute la Gamme en modifiant les dimensions du tuyau par l'ouverture et la fermeture des trous latéraux. Les trous sont si larges que l'extrémité inférieure du tuyau ne joue plus aucun rôle, la Hauteur de la Note étant celle d'un tuyau fictif dont la longueur serait limitée à ce trou. La Note la plus grave se joue avec tous les trous fermés. Les Notes plus aigües sont jouées en ouvrant les trous un à un, à partir de l'extrémité inférieure du tuyau (cf [BENA Les bois]).
- Pour les Cuivres (exemple de la trompette), le musicien exécute la Gamme en utilisant une série de soupapes (pistons) qui allongent ou raccourcissent le tuyau principal en ajoutant ou en court-circuitant de petits éléments de tuyauterie (cf [BENA, Les bois]).
Instruments de percussion (production du son par Membrane vibrante, Plaque vibrante ou autre procédé) :
Les instruments de percussion produisent des Bruits qui sont transformés en Son musicaux de par la manière dont les instruments résonnent.
Les différents modes d'excitation sont les suivants :
- Frappement (caisse, cloche, gong, tambour, xylophone, etc.)
- Raclement (crécelle, racleur, etc.)
- Entrechoc (castagnettes, cymbale, triangle, etc.)
- Pilonnement (bâton, planche, etc.)
- Secousse (grelots, hochet, maracas, sistre, etc.)
- Pincement (guimbarde, etc.)
- Frottement (harmonica de verre, verres musicaux, etc.)
Voir Langage parlé.
Voir Liaison.



La Liaison permet de réaliser un Phrasé sur un groupe de Notes.
On distingue :
- La Liaison de prolongation ou de tenue (symbole = ligne courbe horizontale), qui a pour effet de lier deux Notes de même Hauteur et de Durée quelconque, la seconde Note n'étant pas jouée mais sa Durée venant s'ajouter à celle de la Note précédente (voir Figure 1 ci-dessus),
- La Liaison d'expression ou legato (symbole = ligne courbe horizontale), qui a pour effet de lier plusieurs Intervalles ou Accords, sans rupture de Son (voir Figure 2 ci-dessus),
- Le Glissé ou glissando (symbole = une ou plusieurs barres fines entre Notes), qui consiste à parcourir l'échelle des Hauteurs de façon continue (voir Figure 3 ci-dessus).
Voir Mélodie.
Voir Portée.
Le log est la fonction logarithme. Selon la base (2 ou 10), on a la relation suivante :
log2(x) = log10(x) / log10(2).
La longueur d'onde (λ) est la distance (en mètre) parcourue par une onde au cours d'une Période T.
Si f est la Fréquence, T la Période et c la célérité de l'onde, alors : λ = c T = c/f.
Les pianistes indiquent souvent sur les morceaux musicaux quelle Main doit les jouer. La notation est la suivante :
Editions françaises : M.D. et M.G. pour respectivement Main Droite et Main Gauche.
Editions italiennes : M.D. et M.S. pour respectivement Mano Destra et Mano Sinistra.
Editions allemandes : R.H. et L.H. pour respectivement Rechte Hand et Linke Hand.
Un Accord de trois notes est dit Majeur quand sa Tierce constitutive est Majeure (exemple : do - mi - solb).
Il est dit "Accord parfait majeur" quand, de plus, sa Quinte est juste (exemple : do - mi - sol).
Un Intervalle est dit Majeur quand sa Seconde, Tierce, Sixte ou Septième est Majeure.


Le Mode Majeur est la classe de Gammes diatoniques caractérisées par les Intervalles donnés dans le Tableau ci-dessous.
Il est formé de deux Tétracordes séparés d'un Ton, chaque Tétracorde valant (1 Ton, 1 Ton, 1 Demi-ton).
| Degrés | I | II | III | IV | V | VI | VII | VIII | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mode Majeur | Ton | Ton | 1/2 Ton | Ton | Ton | Ton | 1/2 Ton |
|
A retenir : Le Mode Majeur a une couleur chaude, plutôt joyeuse et lumineuse, donnée par ses deux Tons entiers entre la Tonique I et la Médiante III. |
A noter que toute Gamme prend le Nom de son premier Degré I
La Figure ci-dessus donne deux exemples de Gamme Majeure :
- la Gamme du do majeur (qui est simple à jouer au piano car elle utilise uniquement les touches blanches),
- la Gamme du la majeur.
Voir Degré.
Au niveau de l'exécution instrumentale ou vocale d'un morceau musical, la Mélodie (ou Ligne mélodique) désigne la succession de Notes produites par une seule Voix.
Au niveau de la notation musicale, la Mélodie (ou Plan mélodique) désigne l'organisation en Hauteur des événements musicaux et se caractérise essentiellement par :
- la Portée,
- la Hauteur des Notes (Nom des Notes, Clef, Altération, Intervalle, Accord, Son musical),
- la Structure mélodique (Nuance, Liaison, Ornement),
- la Tessiture des Instruments de musique.
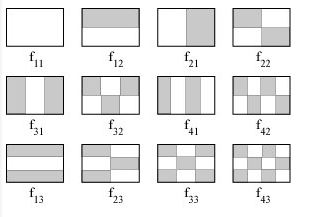

Figures 1 ci-dessus : les 12 premiers modes propres d'une membrane rectangulaire à bords fixés, avec exemple de tambour provençal à cadre carré
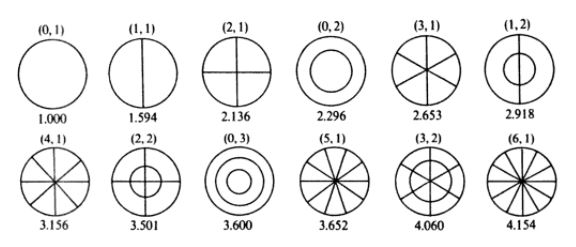
Figures 2 ci-dessus : les 12 premiers modes propres d'une membrane circulaire à bords fixés, avec exemple de grand tambour d'orchestre (à cadre circulaire).




Figures 3 ci-dessus : les 24 premiers modes propres d'une membrane triangulaire équilatérale à bords fixés, avec exemple de tambour provençal à cadre quasi-triangulaire.
Les membranes sont les équivalents en deux dimensions des Cordes vibrantes.
Généralités (communes avec Plaque vibrante) :
- Le son émis par une plaque ou membrane vibrante, bien que constitué de Fréquences fixes, est un son complexe non périodique et ne se décompose pas en Séries de Fourier sous forme d'une somme d'ondes sinusoïdales dont les Fréquences sont des multiples entiers d'une même Fréquence Fondamentale. Les différentes Fréquences propres, dues aux différents Modes propres, peuvent cependant s'approcher plus ou moins bien d'une série Harmonique (cf [KAC]).
- Le Mode propre est défini par un couple (m ≥ 0, n ≥ 0), m et n étant des entiers.
- Les lignes nodales sont l'analogue en deux dimensions des noeuds des Cordes vibrantes.
- Les Modes propres sont dits "dégénérés" lorsque deux ou plusieurs couples (m, n) différents correspondent à la même Fréquence propre fmn. Ces Modes se superposent toujours, la linéarité de l'équation de la vibration transversale (équation d'onde) autorisant la superposition des solutions. Le système nodal est alors fonction des conditions initiales (à t = 0) imposées à la plaque ou à la membrane (cf [NICO, p.94]). A noter que chacun de ces Modes peut exister seul si les conditions initiales s'y prêtent (cf [LAME, p.133]).
Vitesse de propagation de l'onde transversale :
Pour une membrane tendue, la vitesse de propagation (c) de l'onde transversale (en m/s) est la suivante (cf [PASC, p.33]) :
c = (T/M)1/2 avec T = tension linéaire de la membrane (en N/m) et M = masse surfacique (en kg/m2)
L'équation de la vibration transversale se résoud mathématiquement lorsque le contour de la membrane est simple (rectangle, carré, cercle, triangle, etc.) avec les résultats suivants :
Membrane rectangulaire de côtés Lx et Ly, à bords fixés (membrane de la plupart des tambours deff d'Albanie par exemple) :
La Figure 1 ci-dessus donne les 12 premiers Modes propres d'une membrane rectangulaire à bords fixés, pour un rapport Ly/Lx non mentionné par l'auteur (cf [PASC, p.35]). Pour Ly/Lx = 2, [RUSSELL] donne les 12 premiers Modes propres en fonction de leur Fréquence propre.
Pour une Fréquence propre donnée, les lignes nodales peuvent être des droites parallèles aux côtés ou des diagonales ou des courbes diverses (fermées ou ouvertes). Le premier cas concerne tous les Modes propres non dégénérés et toutes les superpositions de Modes propres dégénérés dont tous sauf un ont une amplitude nulle (cf [LAME, p.126] [NICO, p.93]).
Fréquences propres (cf [LAME, p.121] [PASC, p.34] [NICO, p.92] [BOYLE, p.27]) : fmn = (1/2) c ((m / Lx)2 + (n / Ly)2)1/2
Le Mode propre est défini par le couple (m ≥ 1, n ≥ 1), m et n étant respectivement le nombre de ventres selon Ly et Lx (cf [NICO, p.94]).
Le mode fondamental est le mode (1, 1) pour lequel les seules lignes nodales sont sur les bords.
Modes propres dégénérés (cf [LAME, p.122] [NICO, p.93]) : n'existent que dans le cas où le rapport Ly2/Lx2 est un nombre entier ou fractionnaire (cas de rapport commensurable). Exemple de fmn pour Ly2/Lx2 = 4 : f14 = f22 (voir [RUSSEL]).
Déplacement transversal de la membrane (cf [PASC, p.34] [NICO, p.92] [BOYLE, p.28]) : z(x, y, t) = ∑m≥1, n≥1[ (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) sin( m π x / Lx) sin( n π y / Ly) ]
Amn et Bmn = constantes déterminées par les conditions initiales de la membrane (à t = 0).
Membrane carrée de côté L = Lx = Ly, à bords fixés (membrane de la plupart des tambours deff d'Albanie ou de certains tambours provençaux, par exemple) :
Fréquences propres (cf [PASC, p.35] [LAME, p.123]) : fmn = (1/2) (c/L) (m2 + n2)1/2
Modes propres dégénérés (exemples) : f12 = f21 ; f55 = f17 = f71 ; f18 = f81 = f47 = f74.
Membrane circulaire de rayon R, à bords fixés (membrane de la plupart des tambours par exemple) :
La Figure 2 ci-dessus donne les 12 premiers Modes propres d'une membrane circulaire à bords fixés, classés par Fréquences propres croissantes (cf [FLETCH, p.75] [PASC, p.38]).
Fréquences propres (cf [PASC, p.38] [NICO, p.97] [KAC, p.36]) : fmn = (1/(2 π)) (c/R) xmn
Jm(x) = fonction de Bessel de première espèce et d'ordre m
xmn = le n ième zéro de la fonction de Bessel Jm(x), avec les valeurs suivantes pour n ≥ 1 :
x0n = 2.405 ; 5.520 ; 8.654 ; 11.792 ; etc.
x1n = 3.832 ; 7.016 ; 10.173 ; etc.
x2n = 5.136 ; 8.417 ; 11.620 ; etc.
x3n = 6.380 ; 9.761 ; 13.015 ; etc.
x4n = 7.588 ; 11.065 ; etc.
x5n = 8.771 ; 12.339 ; etc.
x6n = 9.936 ; 13.589 ; etc.
x7n = 11.086 ; etc.
Le Mode propre est défini par le couple (m ≥ 0, n ≥ 1), m étant le nombre de diamètres et n le nombre de cercles concentriques (comprenant le bord).
Le mode fondamental est le mode (0, 1) de Fréquence propre f01 = (1/(2 π)) (c/R) (2.405), pour lequel la seule ligne nodale est sur la circonférence.
Modes propres dégénérés : aucun a priori.
Déplacement transversal de la membrane en coordonnées polaires r et θ (cf [ISOZ, p.1856] [BEDARD, p.93]) : z(r, θ, t) = ∑m≥0, n≥1[ Jm(xmn r/R) ( (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) sin(m θ) + (Cmn sin(2 π fmn t) + Dmn cos(2 π fmn t)) cos(m θ) ) ]
Amn, Bmn, Cmn et Dmn = constantes déterminées par les conditions initiales de la membrane (à t = 0).
Remarque 1 (cf [NICO, p.97]) : pour x grand, Jm(x) peut se calculer par la formule asymptotique : Jm(x) = (2/(π x))1/2 cos(x - (π/2)(m + 1/2))
Remarque 2 (cf [NICO, p.97]) : pour n grand, xmn peut se calculer par la formule asymptotique : xmn = π (m/2 + n - 1/4)
Membrane triangulaire équilatérale de côté L, à bords fixés (membrane de certains tambours du Maroc ou de certains tambours provençaux, par exemple) :
La Figure 3 ci-dessus donne les 24 premiers Modes propres d'une membrane triangulaire équilatérale à bords fixés, classés par Fréquences propres croissantes (cf [HILLA, Triangle of area 1]). La numérotation des Modes est a priori la suivante :
Colonne N°1 : (1, 1) (1, 2) (2, 1) (2, 2) (1, 3) (3, 1) (2, 3) (3, 2)
Colonne N°2 : (1, 4) (4, 1) (3, 3) (2, 4) (4, 2) (1, 5) (5, 1) (3, 4)
Colonne N°3 : (4, 3) (2, 5) (5, 2) (1, 6) (6, 1) (4, 4) (3, 5) (5, 3)
Remarque 1 : lorsque m ≠ n, tout Mode propre se partage en un Mode propre symétrique et un autre antisymétrique (cf [McCARTIN, mode(1, 2) pp18-19, mode(1, 4) pp21-23]). Ces deux types de Modes apparaissent sur la Figure 3, groupés par deux, sous la notation arbitraire (m, n) puis (n, m).
Remarque 2 : sur le site de calcul (cf [HILLA, Triangle of area 1]), les valeurs propres λmn indiquées et correspondant à la formule : λmn = (2 π fmn/c)2 sont calculées avec L = 1,52 m. La valeur de l'argument (m2 + n2 + mn) s'obtient alors en divisant λmn par la constante k = ((4 π)/(3 L))2 = 7,60 m-2
Pour une Fréquence propre donnée, les lignes nodales peuvent être des droites parallèles aux côtés ou des médianes ou des courbes diverses (fermées ou ouvertes). Le premier cas concerne tous les Modes propres non dégénérés et toutes les superpositions de Modes propres dégénérés dont tous sauf un ont une amplitude nulle (cf [LAME, p.135]).
Fréquences propres (cf [LAME, pp115, 134 et 135] [McCARTIN, pp38 et 39] [EVEN, p.4]) : fmn = (2/3) (c/L) (m2 + n2 + mn)1/2
Le Mode propre est défini par le couple (m ≥ 1, n ≥ 1), m et n étant des entiers.
Le mode fondamental est le mode (1, 1) de Fréquence propre f11 = (2/(31/2)) (c/L), pour lequel les seules lignes nodales sont sur les bords.
Modes propres dégénérés : Exemples de fmn (cf [LAME, p.135] [McCARTIN, p.25]) : f12 = f21 ; f77 = f2 11 = f11 2 ; f19 = f91 = f56 = f65. Pour m ≠ n, ces Modes sont construits en décomposant la fonction d'onde en deux parties symétrique et antisymétrique par rapport à une médiane (cf [McCARTIN, p.12]).
Déplacement transversal de la membrane : z(x, y, t) = ∑m≥1, n≥1[ (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) Tmn(x, y) ]
Tmn(x, y) = fonction dépendant des entiers m et n (voir [LAME, p.132] [McCARTIN, p.25] [EVEN])
Amn et Bmn = constantes déterminées par les conditions initiales de la membrane (à t = 0).

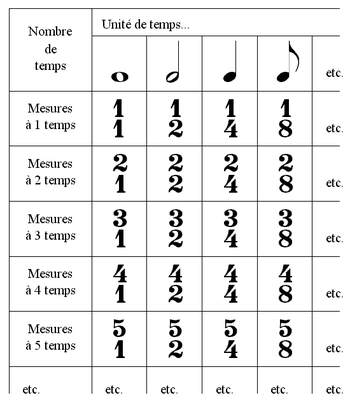
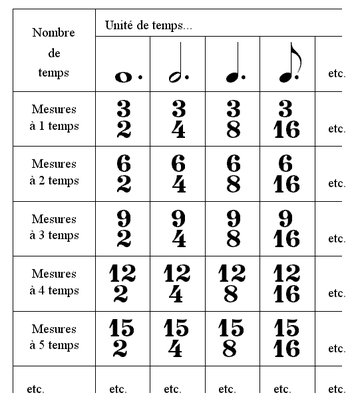
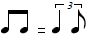
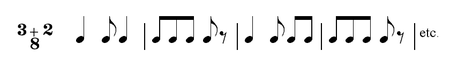
La Mesure est la division d'un morceau musical en parties d'égales durées, identifiées sur la Portée par des Barres de Mesure (voir Figures 1 et 2 ci-dessus).
Le Chiffrage indiqué en début de morceau représente les trois caractéristiques de la Mesure : le Nombre de Temps, l'Unité de Temps et la Structure des Temps (voir Tableau ci-dessous).
Traditionnellement, ce Chiffrage est une fraction (N/D) de deux nombres entiers (sans la barre horizontale). Le Chiffrage 4/4 est parfois représenté par un "C", et le Chiffrage 2/2 par un "C" barré.
Attention, ce Chiffrage traditionnel est ambigu lorsque le numérateur est multiple de 3. Les deux exemples suivants montrent que le Chiffrage "3/2" peut aussi bien concerner une Mesure simple (formée de 3 Notes de valeur 1/2 Ronde, soit 3 Blanches) qu'une Mesure composée (formée de 1 Note de valeur 3/2 Ronde, soit 1 Ronde pointée). Seul le contexte du morceau musical permet de lever l'ambiguïté.
En notation moderne, afin d'éviter toute ambiguïté, le Chiffrage est le suivant :
- soit il est suivi entre parenthèses du Nombre de temps. Le Chiffrage "3/2" s'écrit alors : 3/2 (3) pour la Mesure simple à 3 Temps et 3/2 (1) pour la Mesure composée à 1 Temps.
- soit il ne comporte qu'un seul nombre (Nombre de Temps) et l'Unité de Temps apparaît au-dessus ou au-dessous de ce nombre sous forme d'une Figure de Note. Le Chiffrage "3/2" s'écrit alors : chiffre 3 accompagné d'une Blanche pour la Mesure simple et chiffre 1 accompagné d'une Ronde pointée pour la Mesure composée.
Au-delà du Chiffrage, la Mesure est caractérisée par l'Accentuation des Temps. Généralement, la Mesure comporte un Temps fort (plutôt le premier en musique classique, plutôt le second et le quatrième en musique jazz/rock) suivi de x Temps faibles.
La notion fort/faible n'est pas nécessairement liée à l'accentuation de l'Intensité des Sons musicaux. L'orgue par exemple est incapable de produire une différence d'Intensité sur certains Temps. La notion fort/faible ressentie par l'auditeur réceptif résulte alors de l'organisation du discours musical.
| Caractéristique | Chiffrage de la Mesure |
|---|---|
| Nombre de Temps |
C'est le nombre de Temps utilisés dans la Mesure. Le numérateur (N) de la fraction est un nombre entier qui indique le nombre de Temps (pour une Mesure simple) ou le nombre de tiers de Temps (pour une Mesure composée) ou rien d'évident (pour une Mesure asymétrique). |
| Unité de Temps |
C'est la Figure de Note dont la durée est égale à un Temps. Le dénominateur (D) de la fraction est un nombre entier qui indique une fraction (1/D) de Ronde (par exemple : D = 4 correspondant à 1/4 Ronde soit une Noire). Cette fraction vaut un Temps (pour une Mesure simple) ou un tiers de Temps (pour une Mesure composée) ou rien d'évident (pour une Mesure asymétrique). |
| Structure des Temps |
Elle est binaire, ternaire ou asymétrique, comme ainsi défini : La structure binaire ou Mesure simple est la Mesure à Temps égaux binaires pour laquelle l'Unité de Temps est une Figure de Note non pointée (voir Tableau 1 ci-dessus). Le Chiffrage d'une Mesure simple est alors la fraction N/D = N x (1/D) pour laquelle la Nombre de Temps vaut N et l'Unité de Temps vaut la fraction 1/D de Ronde. Exemple : le Chiffrage "3/2" signifie qu'il y a 3 Temps dans la Mesure et que l'Unité de Temps est une Blanche de valeur un Temps. Attention, dans le domaine musical Jazz/Rock, une partition à Chiffrage binaire doit être interprétée de façon ternaire lorsqu'on trouve en début de partition les symboles "shuffle" ou "swing feel" ou une indication de division du Temps par un multiple de 3 (voir exemple en dernière Figure de gauche ci-dessus). La structure ternaire ou Mesure composée est la Mesure à Temps égaux ternaires pour laquelle l'Unité de Temps est une Figure de Note pointée (voir Tableau 2 ci-dessus). Le Chiffrage d'une Mesure composée (avec N multiple de 3) est alors la fraction N/D = (N/3) x (3/D) pour laquelle le Nombre de Temps vaut N/3 et l'Unité de Temps vaut la fraction 3/D de Ronde. Exemple : le Chiffrage "3/2" signifie qu'il y a 3 tiers de Temps dans la Mesure (soit un seul Temps par Mesure) et que l'Unité de Temps est une Blanche de valeur un tiers de Temps (soit une Ronde pointée de valeur un Temps). La structure asymétrique ou Mesure asymétrique est la Mesure ayant des Temps inégaux ou bien un Nombre de Temps non entier. Le numérateur du Chiffrage peut comporter plusieurs nombres de durées différentes. Le dénominateur indique une Figure de note, comme dans le Chiffrage habituel. Dans de longues Mesures, on rajoute parfois une Barre de Mesure pointillée pour mieux délimiter les parties de la Mesure. Pour le Tempo, c'est la valeur rythmique la plus courte qui sert alors de pulsation. Exemple 1 (voir exemple en dernière Figure de droite ci-dessus) : le Chiffrage "3+2 sur 8" indique une Mesure à deux Temps inégaux : le premier Temps est ternaire (Unité de Temps : la Noire pointée), le second est binaire (Unité de Temps : la Noire) et plus court que le premier. Exemple 2 : le Chiffrage "2/8 + 2/8 + 3/8" indique une Mesure à trois Temps inégaux : deux Temps binaires (Unité de Temps : la Noire) et un Temps ternaire (Unité de Temps : la Noire pointée). Exemple 3 : le Chiffrage "3/4 + 1/8" indique une Mesure à trois Temps et demi : trois Temps binaires (Unité de Temps : la Noire) et un demi-Temps binaire (Unité de Temps : la Noire). |
Un Accord de trois notes est dit Mineur quand sa Tierce constitutive est Mineure (exemple : do - mib - solb).
Il est dit "Accord parfait mineur" quand, de plus, sa Quinte est juste (exemple : do - mib - sol).
Un Intervalle est dit Mineur quand sa Seconde, Tierce, Sixte ou Septième est Mineure.
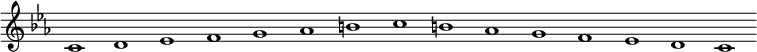
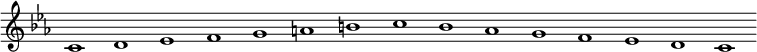
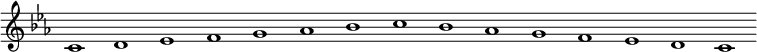



Le Mode mineur est la classe de Gammes diatoniques caractérisées par les Intervalles donnés dans le Tableau ci-dessous.
Il est formé de deux Tétracordes séparés d'un Ton, le premier Tétracorde valant (1 Ton, 1 Demi-ton, 1 Ton), le second variant en fonction du type de Mode.
| Degrés | I | II | III | IV | V | VI | VII | VIII | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mode Majeur (pour comparaison) | Ton | Ton | 1/2 Ton | Ton | Ton | Ton | 1/2 Ton | ||||||||
| Mode Mineur harmonique ou classique | Ton | 1/2 Ton | Ton | Ton | 1/2 Ton | 3/2 Ton | 1/2 Ton | ||||||||
| Mode Mineur mélodique ascendant | Ton | 1/2 Ton | Ton | Ton | Ton | Ton | 1/2 Ton | ||||||||
| Mode Mineur naturel ou mélodique descendant | Ton | 1/2 Ton | Ton | Ton | 1/2 Ton | Ton | Ton |
|
A retenir : Le Mode Mineur harmonique ou classique se déduit du Mode Majeur par un simple abaissement des Degrés III et VI (cf [FAB Le mineur]). En do mineur, le mi devient ainsi un mib et le la devient un lab. En la mineur, le do# devient un do et le fa# devient un fa. Voir Figure ci-dessus (à comparer avec Figure de la Gamme Majeure). Le Mode Mineur harmonique se déduit du Mode Mineur naturel par un simple haussement du Degré VII sous forme d'une Altération accidentelle (voir Figure ci-dessus). Le Mode Mineur harmonique est très utilisé en musique classique et a une couleur légèrement "Orientale" donnée par l'encadrement du 3/2 Ton entre les deux 1/2 Ton. Le Mode Mineur mélodique ascendant se déduit du Mode Mineur harmonique par un simple haussement du Degré VI (cf [FAB Le mineur]). En do mineur, le lab devient ainsi un la. En la mineur, le fa devient un fa#. Voir Figure ci-dessus. Le Mode Mineur mélodique ascendant se déduit du Mode Mineur naturel par un simple haussement des Degrés VI et VII sous forme de deux Altérations accidentelles (voir Figure ci-dessus). Le Mode Mineur mélodique ascendant est très utilisé par les chanteurs car le 3/2 Ton du Mode Mineur harmonique, peu mélodique et d'intonation difficile, se trouve ramené à un Ton. Le Mode Mineur naturel ou mélodique descendant se déduit du Mode Mineur mélodique ascendant par un simple renversement des trois derniers Intervalles V-VI, VI-VII et VII-VIII (cf [FAB Le mineur]), ce qui revient à baisser les Degrés VI et VII du Mode Mineur mélodique ascendant. En do mineur, le la devient ainsi un lab et le si devient un sib. En la mineur, le fa# devient un fa et le sol# devient un sol. Voir Figure ci-dessus. Le Mode Mineur naturel se confond avec le Mode médiéval Eolien (ou Mode de la) issu du Degré VI de la gamme Majeure. Majeure ; Le Mode Mineur naturel est très utilisé dans les ballades car ses absences de tensions (notamment sa Sensible VII placée à un Ton loin de la Tonique VIII) le rendent plutôt doux, calme et tendre, voire "gentiment mélancolique". Mais il peut aussi sonner de manière émue ou passionnée, notamment en reggae et rock. |
A noter que toute Gamme prend le Nom de son premier Degré I
La Figure ci-dessus donne six exemples de Gamme mineure :
- la Gamme du do mineur harmonique,
- la Gamme du do mineur mélodique,
- la Gamme du do mineur naturel,
- la Gamme du la mineur harmonique (qui est celle utilisée couramment en Musique Tonale et qui se déduit de la Gamme du la mineur naturel par l'Altération accidentelle du sol en sol#),
- la Gamme du la mineur mélodique,
- la Gamme du la mineur naturel (qui est simple à jouer au piano car elle utilise uniquement les touches blanches).
La Musique Modale est une Musique à sept Modes construits à partir de chaque Note naturelle.
Ces Modes incluent les quatre Modes employés au Moyen Âge, auxquels furent ajoutés les Modes de do et de la au cours de la Renaissance au 15e siècle puis le Mode de si au cours du 19e siècle.
Le Tableau suivant donne la description des sept Modes de la Musique Modale.
A noter que ces Modes comprennent chacun 5 Tons et 2 Demi-tons, et ne sont mathématiquement que les rotations de la même échelle diatonique naturelle (Gamme du do majeur).
| Nom moderne | Nom courant | Intervalles en Tons |
|---|---|---|
| Mode de do (ou Gamme de do majeur) | Mode ionien | 1 - 1 - 1/2 - 1 - 1 - 1 - 1/2 |
| Mode de ré | Mode dorien | 1 - 1/2 - 1 - 1 - 1 - 1/2 - 1 |
| Mode de mi | Mode phrygien | 1/2 - 1 - 1 - 1 - 1/2 - 1 - 1 |
| Mode de fa | Mode lydien | 1 - 1 - 1 - 1/2 - 1 - 1 - 1/2 |
| Mode de sol | Mode mixolydien | 1 - 1 - 1/2 - 1 - 1 - 1/2 - 1 |
| Mode de la (ou Gamme de la mineur naturel) | Mode éolien | 1 - 1/2 - 1 - 1 - 1/2 - 1 - 1 |
| Mode de si | Mode locrien | 1/2 - 1 - 1 - 1/2 - 1 - 1 - 1 |
La Musique Modale a été abandonnée au cours du 17e siècle au profit de la Musique Tonale fondée sur deux Modes exclusifs : le Mode Majeur et le Mode Mineur.
Cette évolution est due essentiellement au fait que la plupart des modes anciens ne possèdent pas de note sensible (Degré VII élevé, situé seulement à un Demi-ton en dessous de la Tonique (Degré I)), élément essentiel pour créer une tension harmonique forte se résolvant naturellement vers la Tonique.
Dans le mode du fa (lydien), bien qu'une note sensible soit présente, sa tension est affaiblie par la présence simultanée de la quarte augmentée (Degré #IV).
Dans la mode du la mineur naturel (éolien), la note sensible est absente et la Musique Tonale préfère utiliser les formes du Mineur harmonique et du Mineur mélodique qui rétablissent cette tension vers la Tonique.
Ainsi, l'absence de note sensible dans la plupart des modes anciens limitait la force dramatique et la clarté des progressions harmoniques.
La Musique Modale a été ensuite redécouverte et adaptée au cours du 19e siècle afin de retrouver une liberté mélodique, une pureté d'expression et une richesse de couleurs, perçues comme une alternative au formalisme tonal.
Voir Majeur (Mode) et Mineur (Mode).
En Musique tonale, la modulation est le changement durable de la Tonalité d'un morceau musical. Le changement concerne le Ton mais peut aussi concerner le Mode (Majeur ou Mineur).
Lorsque le changement se limite à peu d'Accords pour revenir à la Tonalité initiale, on parle alors d'Emprunt, voire de Dominante secondaire.
Le changement s'effectue généralement par l'emploi d'un ou plusieurs Accords de transition, appelés aussi Accords mixtes car appartenant à la fois aux deux Tonalités (initiale et nouvelle).

Le Mordant (symbole = petite vague horizontale) et le Mordant inverse (symbole = petite vague horizontale et barrée) sont des Ornements particuliers (voir Figure ci-dessus). Chacun est une portion de Trille sur trois Notes.
Dans le Langage parlé, un Mot est une suite ininterrompue de Syllabes. Le Mot "opérateur" par exemple comprend quatre Syllabes (o.pé.ra.teur).
Le Mouvement d'une Oeuvre musicale est un des morceaux musicaux de l'oeuvre. Exemple : le "premier Mouvement de la Symphonie héroïque".
Voir Tempo.

En musique occidentale, le Mouvement des Voix désigne la progression du tissu musical selon l'axe des Hauteurs, aussi bien sur le plan Mélodique (horizontal) que sur le plan Harmonique proprement dit (vertical).
Le Mouvement mélodique est l'Intervalle mélodique parcouru par une même Voix entre deux Notes successives. Le Mouvement peut être ascendant ou descendant.
Dans le Contrepoint, le Mouvement mélodique doit respecter deux principes :
- Principe de l'économie de mouvement : toute Note commune à deux Degrés ou Accords qui s'Enchaînent doit, si possible, rester en place à la même Voix.
- Principe du plus court chemin : le Mouvement Conjoint doit toujours être préféré au Mouvement Disjoint.
Les principes de l'Harmonie sont beaucoup moins stricts et autorisent les Mouvements Disjoints de type : Tierce (majeure ou mineure), Quarte juste, Quinte juste, Sixte mineure et Octave juste.
Le Mouvement harmonique est la somme d'au moins deux Mouvements mélodiques simultanés. Il peut être Parallèle, Contraire ou Oblique (voir Figure ci-dessus et [FAB Unité 2.1]) :
- Le Mouvement est Parallèle lorsque deux Lignes mélodiques montent ou descendent en même temps, selon un Intervalle généralement constant. Ce mouvement est parfois appelé Direct lorsque l'Intervalle n'est pas constant.
- Le Mouvement est Contraire lorsqu'une une ligne mélodique monte alors que l'autre descend.
- Le Mouvement est Oblique lorsqu'une des deux Lignes mélodiques reste constante.
Le Mouvement harmonique doit respecter a minima les principes suivants (cf [BAR Cours]) :
- Les Croisements de Voix sont à éviter.
- Par mouvement Parallèle, les Quintes, Octaves et Unissons consécutifs sont interdites, sauf effet voulu, car jugés trop durs (pour les Quintes) et trop plats (pour les Octaves et Unissons).
- Par mouvement Contraire, les Quintes et Octaves consécutifs et les successions Octave-Unisson ou Unisson-Octave sont interdits pour la même raison.
- Par mouvement Direct, l'Unisson est interdit.
- Par mouvement Direct, il faut limiter l'effet marquant des Quintes et Octaves que le mouvement amène. L'une des deux Voix doit être Conjointe (idéalement celle du dessus).
- Par mouvement Oblique, au moment d'un Unisson, il n'est pas élégant d'y arriver par mouvement Conjoint de la voix qui bouge.
Une Note naturelle est une Note sans Altération de type dièse, double dièse, bémol ou double bémol, le bécarre étant autorisé
La Neuvième est l'Intervalle qui sépare neuf Degrés consécutifs dans la Gamme diatonique. Elle est constitué d'une Seconde augmentée d'une Octave juste. On parle aussi d'Intervalle "Redoublé à l'Octave".
Voir Figure de Note.

En musique occidentale (France, Italie, Espagne et autres pays (Bulgarie, Thaïlande, etc.)), les Notes de la Gamme diatonique ont pour Noms : "do, ré, mi, fa, sol, la, si" (voir Figure ci-dessus).
Ces Notes ont été inventées par le moine Guido d'Arezzo en 1028 qui s'est inspiré de l'Hymne à Saint Jean-Baptiste, un chant religeux latin attribué au moine et érudit Paul Diacre :
Ut queant laxis / resonare fibris / mira gestorum / famuli tuorum / solve polluti / labii reatum / Sancte Iohannes
Traduction : Pour nous permettre de chanter à pleine voix les merveilles de tes actions, efface le péché de nos lèvres impures, Ô Saint Jean
Le ut sera remplacé plus tard par le do et subsiste encore, notamment avec la Clef d'ut.
Dans les pays anglo-saxons, les Notes sont les lettres "A, B, C, D, E, F, G" correspondant respectivement aux Notes "la, si, do, ré, mi, fa, sol" listées depuis le la.
Dans les pays de langue allemande, B désigne le sib, H le si et S le mi bémol. Ainsi, Jean-Sébastien Bach utilisait comme "signature" les quatre Notes sib-la-do-si, soit B-A-C-H
Pour les Altérations, le dièse et le bémol s'écrivent respectivement sharp et flat en anglais. En allemand, la Note est suivie respectivement de "-is" (pour le dièse) et de "-es" ou "-s" (pour le bémol).
La Note est un Son musical caractérisé par un Nom, une Hauteur et une Durée.


En musique occidentale, une Nuance est un symbole qui indique l'Intensité relative d'une Note, d'une Phrase musicale, ou encore d'un morceau entier d'une oeuvre musicale.
La Nuance est placée au-dessus ou au-dessous d'une Note et affecte toutes les Notes suivantes jusqu'à indication contraire (voir Figure 1 ci-dessus).
Exemples par ordre d'Intensité croissante : "pp" pour pianissimo, "p" pour piano, "mf" pour mezzo-forte, "f" pour forte.
La Nuance peut subir une accentuation propre sur certaines Notes (voir Figure 2 ci-dessus) :
Exemples : Attaque puissante (1), modérée (2) ou tenue (3).
La Nuance peut subir une variation (voir Figure 1 ci-dessus) :
Exemples d'augmentation : "cresc." pour crescendo, "rf" pour rinforzando, "sf" pour sforzando, "<" pour une augmentation progressive sur un ensemble de Notes.
Exemples de diminution : "decresc." pour decrescendo, "dim." pour diminuendo, "smorz." pour smorzando, "mor." pour morendo, "cal." pour calando, ">" pour une diminution progressive sur un ensemble de Notes.
L'Octave est l'Intervalle qui sépare huit Degrés consécutifs dans la Gamme diatonique.
L'Octave juste correspond à 5 Tons et 2 Demi-tons. Il a pour rapport 2/1. Exemple en do Majeur : do - do.
L'Octave est numérotée pour distinguer deux Notes de même Nom dans deux Octaves différentes. Ainsi, les "la" de Hauteurs respectives 110, 220 et 440 Hz se nomment "la1, la2 et la3".
L'Octave élargie est l'Octave dont l'Intervalle est légèrement supérieur à 2. Les cordes de piano ont par exemple une légère raideur qui font que les Harmoniques supérieurs ont des Fréquences légèrement supérieures aux multiples entiers (2f, 3f, 4f, etc.) de la Fréquence Fondamentale (f).
Opus est le mot latin pour "oeuvre" ou "ouvrage", utilisé notamment en musique et en architecture.
En musique classique :
Le mot "opus" (noté "op.") suivi d'un numéro est utilisé pour des oeuvres musicales classées en fonction de leur date de composition ou de publication.
Le numéro d'opus indique la place de l'oeuvre dans l'ensemble des oeuvres du compositeur. Il est généralement attribué par le compositeur lui-même et plus rarement par les éditeurs de Catalogue.
Ce numéro est indiqué par le sigle "n°" en français, "no." en anglais et "Nr." en allemand.
Attention : Dans de rares cas, certaines oeuvres ont été publiées par des éditeurs différents avec le même numéro d'Opus. Par exemple, pour les oeuvres de Johann Christian Bach, l'opus 18 désigne ses "Six grandes ouvertures" (1778, W. Forster), mais aussi ses "Deux symphonies" (1785, J. Schmitt) et ses "Quatre sonates et deux duos" (1791, J. Welker). Les opus de Boccherini connaissent la même confusion éditoriale.
Certaines oeuvres mineures ou non publiées portent l'indication latine "op. deest" signifiant "opus faisant défaut", ou l'indication allemande "WoO" (Werk ohne Opuszahl) ou "o. Op." (ohne Opuszahl).
Certaines oeuvres posthumes portent parfois l'indication "op. posth.".
Le numéro d'opus est parfois complété d'une lettre accolée (a , b, c) ou d'un mot accolé (bis, ter), généralement pour différencier certains arrangements.
Ainsi, dans le Titre "Variations et fugue sur un thème de Mozart, op. 132/132a (1914), de Max Reger", la première version est pour orchestre, la deuxième est un arrangement pour deux pianos.
Le numéro d'opus est parfois suivi d'un numéro de composition, appelé parfois "numéro d'ordre" (exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, de Georg Friedrich Haendel).
Ainsi, op. 7 n°2 signifie qu'il s'agit de la deuxième oeuvre d'un groupe d'oeuvres portant le numéro d'opus 7.
Attention à ne pas confondre le "numéro d'ordre" de l'Opus avec le numéro d'ordre du Genre qui apparaît en début du Titre.
De nos jours, l'opus est relativement délaissé, la singularité des Titres permettant de s'en dispenser.
L'Ornement est une Note ou un groupe de Notes ajouté à une Mélodie pour l'embellir. On distingue notamment :
- Le Vibrato,
- Le Trille,
- Le Mordant,
- Le Tremolo de répétition,
- Le Tremolo trille,
- L'Appogiature.
Voir Voix.
Voir Voix.
Voir Harmoniques.
En Langage parlé, la Pause est un des composants de la Prosodie qui est soit une pause silencieuse (Pause musicale), soit une pause nourrie (allongement exceptionnel d'une Syllabe ou production d'interjections telles que "euh" ou "hum").
Voir Figure de Silence.
La Période est la durée T (en seconde) séparant deux états vibratoires identiques et successifs d'un point du milieu dans lequel l'onde se propage.
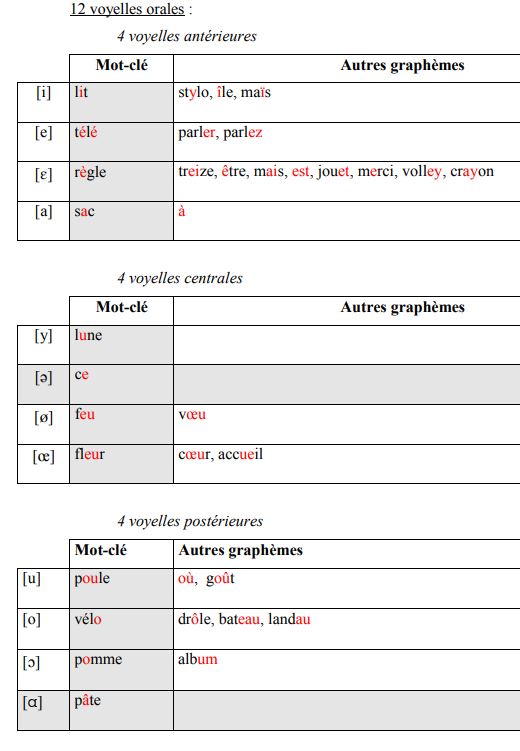
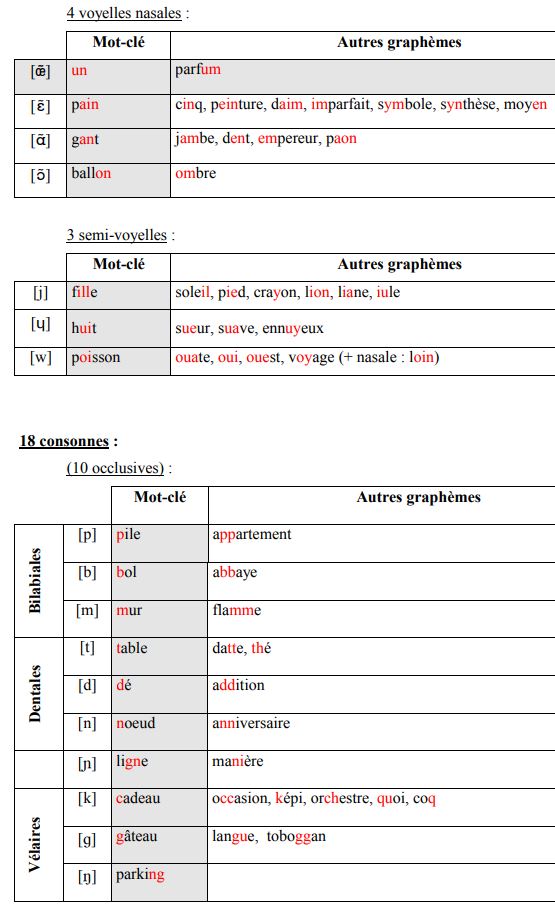

Notation :
Le Phonème est la plus petite unité que l'on puisse isoler par segmentation dans la chaîne parlée.
Les Phonèmes des langues du monde sont répértoriées dans la base de données UPSID (UCLA Phonological Segment Inventory Database), basée sur 451 langues avec 652 Consonnes et 180 Voyelles.
Les Voyelles sont caractérisées par le libre passage de l'air dans le Conduit vocal. Les Consonnes, au contraire, sont caractérisées par l'obstruction momentanée (complète ou partielle) du passage de l'air.
Le français comprend 37 Phonèmes classiques : 16 Voyelles, 3 Semi-voyelles (ou Semi-consonnes), et 18 Consonnes (voir Figure ci-dessus ou Fichier Phonétique (.pdf, 63 ko)).
A l'écrit, un Phonème se représente phonologiquement par une lettre placée entre des barres obliques // ou des crochets []. Par exemple : /y/ correspondant à la prononciation "u".
A l'écrit également, un Phonème se représente orthographiquement par une ou deux lettres placées entre des guillemets. La représentation la plus simple est la suivante (cf [PIET]), en suivant l'ordre de listage de la Figure ci-dessus :
- Voyelles : "i", "é", "è", "a", "u", "e", "eu", "oe", "ou", "au", "o", "â", "un", "in", "an", "on".
- Semi-voyelles (ou Semi-consonnes) : "y", "u+", "w". La première a pour nom technique : yod ou ié, la seconde : ué, la troisième : wau ou oué.
- Consonnes : "p", "b", "m", "t", "d", "n", "gn", "k", "g", "nk/ng", "f", "v", "s", "z", "ch", "j", "l", "r".
Pour les Consonnes, on peut en rajouter trois autres, très peu utilisées en français :
"h aspiré" qui est la Consonne glottale , laquelle est en fait soufflée ou expirée, et toujours placée devant une Voyelle (exemples : interjections "ha" et "hop", verbe "ahaner", mot "hotte" prononcé en région de Liège).
"J" qui est la Consonne vélaire appelée "Rota" en français, "Jota" en espagnol (exemple : "Juan Carlos" en prononciation espagnole) et "Ach-Laut" en allemand (exemple : "Jean-Sébastien Bach" en prononciation allemande).
"rrr" qui est la Consonne r roulé ou r trillé équivalente en français à la Consonne "r" prolongée en durée (exemple : "terre" avec prononciation monégasque).
A noter que le Son "x" en français (comme dans les mots "taxer" ou "exercer") n'est pas un Phonème mais se compose de deux Consonnes de la forme "k" + "s" (exemple : mot "taxer") ou "g" + "z" (exemple : mot "exercer").
Le Tableau des Formants ci-dessous donne la correspondance entre les deux écritures phonologique et orthographique.
Les Phonèmes font par ailleurs l'objet d'un symbolisme phonétique.
Terminologie :
- Le terme "articulatoire" est relatif à l'endroit où se place la langue pour obstruer le passage du flux d'air : lèvres (articulation labiale), dents et alvéoles (articulation dentale), palais dur (articulation palatale), voile du palais et luette (articulation vélaire).
- Le terme "fricative ou constrictive" désigne l'obstruction partielle du passage de l'air, avec friction de l'air sur différents organes.
- Le terme "glissante" ou "glide" en anglais est relatif aux Semi-voyelles, ayant une durée plus brève que celle des Voyelles correspondantes.
- Le terme "glottale" est relatif à la glotte du larynx délimitée par les cordes vocales.
- Le terme "gutturale" ou "rauque" était anciennement relatif à l'ensemble des Consonnes produites par la gorge : Consonnes glottales ("h aspiré"), vélaires ("k", "g", "nk/ng", "r", "J", "w") et palatales ("ch", "j"). De nos jours, il est relatif seulement aux Consonnes vélaires.
- Le terme "liquide" ou "coulante" est relatif à des Consonnes qui, étant employées à la suite d'une autre Consonne dans un même Son, se prononcent facilement.
- Le terme "nasale" ou "oralo-nasale" signifie que le passage de l'air se fait également par les fosses nasales (en plus de la bouche), le voile du palais étant abaissé.
- Le terme "occlusive" désigne l'obstruction complète du passage de l'air, suivie de son relâchement provoquant le Son.
- Le terme "orale" signifie que le passage de l'air se fait uniquement par la bouche, le voile du palais étant relevé.
- Le terme "ouverture" est relatif à la position verticale de la langue par rapport au palais dans l'émission d'une Voyelle : ouverte, mi-ouverte, fermée.
- Le terme "plosive ou explosive" signifie "occlusive orale".
- Le terme "sonante" ou "vocalique" est relatif à l'ensemble des Consonnes nasales, des Consonnes liquides et des Semi-voyelles, lesquelles présentent le degré d'obstacle le plus faible à l'émission du Son.
- Le terme "spirante" ou "approximante" était anciennement relatif à l'ensemble des Consonnes Fricatives. De nos jours, il est relatif seulement aux Consonnes liquides et Semi-voyelles, lesquelles sont produites par une obstruction modérée du passage de l'air qui s'écoule sans le bruit caractéristique de friction des Fricatives.
- Le terme "vibrante" n'est pas relatif aux cordes vocales mais aux Articulateurs mis en vibration (luette ou pointe de la langue).
- Le terme "voisée" ou "sonore" est relatif au Voisement. Il signifie que les cordes vocales vibrent. Dans le cas contraire, on emploie le terme "non-voisée" ou "sourde".
Type de phonèmes :
Le Tableau ci-dessous donne la définition de chaque type de Phonème en prononciation française.
| Type de Phonème | Définition en prononciation française |
|---|---|
| Voyelle |
Au niveau articulatoire, les Voyelles se caractérisent comme suit : - antérieure (ou palatale non arrondie) : fermée ("i", "é"), ouverte ("è", "a"). - centrale (ou palatale arrondie) : fermée ("u", "eu"), mi-ouverte ("e"), ouverte ("oe"). - postérieure (ou vélaire) : fermée ("ou", "au"), ouverte ("o", "â"). - nasale : ouverte ("un", "in", "an"), mi-ouverte ("on"). Au niveau acoustique, les Voyelles se caractérisent comme suit : - orales sonores : les douze premières Voyelles de la Figure ci-dessus, pouvant se répartir en : - aigües : "i", "é", "è", "a", "u", "e", "eu", "oe". - graves : "ou", "au", "o", "â". - nasales sonores : les quatre dernières Voyelles de la Figure ci-dessus, pouvant se répartir en : - aigües : "un" et "in", chaque nasale correspondant à une Voyelle orale ("oe" pour "un" et "è" pour "in"). - graves : "an" et "on", chaque nasale correspondant à une Voyelle orale ("a" pour "an" et "o" pour "on"). Les Voyelles nasales sont toujours perçues comme étant plus longues, moins intenses, plus compactes, plus graves et plus dynamiques que les Voyelles orales correspondantes (cf [DELV Contrôle et connaissance phonétique, p.263]), avec un effet doux et voilé (cf [DELA Attributs]). En français moderne, la Voyelle nasale "un" est en voie de disparition et se prononce "in". Tension phonétique : en français, toutes les Voyelles sont "tendues" (fortement articulées) et aucune n'est "relâchée". Formants : - Les Voyelles orales se différencient sur un Sonagramme essentiellement par leurs Formants F1 et F2 (voir Figure 5 dans Sonagramme). Le Formant F3 est cependant utile pour lever certaines ambiguïtés, notamment la distinction entre le "i" et le "u" chez certains locuteurs pour lesquels les Formants F2 sont proches (voir Tableau des Formants ci-dessous). - Les Voyelles nasales ("un" ; "in" ; "an" ; "on") se différencient des Voyelles orales correspondantes (resp. "oe" ; "è" ; "a" ; "o") par une baisse d'Intensité des trois Formants F1, F2 et F3, avec globalement un Formant F1 plus élevé et un Formant F2 plus bas (cf [MEYN p.14] [DELV Propriétés acoustiques]). |
| Semi-voyelle (ou Semi-consonne) |
Les Semi-voyelles (ou Semi-consonnes) sont acoustiquement très proches de Voyelles ("i" pour "y", "u" pour "u+", "ou" pour "w") et phonologiquement semblables à des Consonnes (car étant toujours suivies d'une Voyelle, le tout formant une seule Syllabe). Au niveau acoustique, elles sont "orales sonores" et peuvent se répartir comme leurs Voyelles correspondantes en : - aigües : "y", "u+". - graves : "w". En français de Belgique, la Semi-voyelle "u+" est prononcée "w". Formants : - Les Semi-voyelles ("y" ; "u+" ; "w") possèdent des Formants qui ressemblent à ceux des Voyelles correspondantes (resp. "i" ; "u" ; "ou") mais avec une durée plus brève (cf [MEYN p.18]). |
| Consonne |
Au niveau articulatoire et acoustique, les Consonnes peuvent se caractériser par le type d'obstruction du passage de l'air, comme suit : - Consonnes occlusives : - orales (ou plosives ou explosives) sourdes : labiale "p", dentale "t", vélaire "k". - orales (ou plosives ou explosives) sonores : labiale "b", dentale "d", vélaire "g". - nasales sonores : "m", "n" et "gn", "nk/ng", chaque nasale correspondant au groupe d'occlusives orales ("p" "b" pour "m" ; "t" "d" pour "n" et "gn" ; "k" "g" pour "nk/ng"). - Consonnes fricatives ou constrictives : - orales sourdes : fuyante "f", sifflante "s", chuintante "ch", glottale "h aspiré", vélaire "J". - orales sonores : fuyante "v", sifflante "z", chuintante "j", liquide latérale "l", liquide vibrante "r", glissantes "y" "u+" "w". En français moderne, la Consonne "gn" est en voie de disparition et se prononce "n" + "y". La Consonne "nk/ng" est au contraire assez récente (exemples : mots "bunker", "parking", "ping-pong", "kung-fu"). La Consonne "J" se prononce "r" en français. Tension phonétique : - Les Consonnes sonores sont toujours perçues comme étant plus graves, grandes, sombres et arrondies que les Consonnes sourdes correspondantes (cf [NOBI p.155]). - En français, toutes les Consonnes sonores sont "douces" et toutes les sourdes sont "fortes". Il existe une loi de compensation de l'énergie musculaire : une occlusive sonore est moins forte qu'une occlusive sourde car une partie de l'énergie musculaire a été utilisée pour le Voisement (cf [KALM parag. 3.7]). Formants : - Les Consonnes sonantes possèdent des Formants comme suit : - Les Consonnes occlusives nasales ("m" ; "n" et "gn" ; "nk/ng") se différencient des groupes de Consonnes orales correspondantes (resp. "p" "b" ; "t" "d" ; "k" "g") par la présence supplémentaire de trois Formants de Hauteur fixe (cf [MEYN p.19]) : il suffit d'introduire un Formant bas vers 250 Hz, un Formant vers 900 Hz et un autre vers 2000 Hz pour qu'une Consonne orale soit perçue comme nasale (cf [PETE p.571] en référence à Delattre 1955). - La Consonne fricative liquide vibrante "r" est caractérisée par la présence de stries verticales claires au cours de la Consonne correspondant à la chute d'énergie due aux micro-occlusions issues du battement répété de l'Articulateur (cf [MEYN p.17]). Cette présence est accompagnée d'un Bruit de friction réduit (cf [MEYN p.29] et très doux [MUNO p.110]). - La Consonne fricative liquide latérale "l" a une structure formantique complexe (cf [MEYN p.18]), accompagnée d'un Bruit de friction très faible (cf [MUNO p.111]). - Les Semi-consonnes (ou Semi-voyelles) possèdent des Formants : voir paragraphe ci-dessus. - Les autres Consonnes n'ont pas de Formants et se différencient des Consonnes sonantes par la présence de Bruit, avec de faibles composantes formantiques (cf [MEYN p.19]). Ces Consonnes se caractérisent sur un Sonagramme par des Transitions de Formant (voir Figures 6 et 7 dans Sonagramme) et se différencient essentiellement les unes des autres comme suit : - Les trois groupes de Consonnes occlusives orales "p" et "b", "t" et "d", "k" et "g", ont un Bruit d'explosion respectivement grave/aigu/medium en Hauteur et moyen/faible/fort en Intensité, le groupe "k" et "g" ayant par ailleurs un Bruit d'explosion bien marqué et précis (lisible) sur un Sonagramme (cf [MUNO p.58]). - Les trois groupes de Consonnes fricatives "f" et "v", "s" et "z", "ch" et "j", ont un Bruit de friction respectivement faible/fort/fort en Intensité (cf [MUNO p.58]). - Les Consonnes fricatives "h aspiré" et "J" ont un Bruit de friction a priori fort en Intensité. |
Fréquences des Formants :
Le Tableau ci-dessous (cf [CHIR]) donne en prononciation française les Fréquences moyennes en Hz des trois premiers Formants des Voyelles et des Consonnes sonantes pour une voix d'homme. Pour une voix de femme, les Fréquences sont sensiblement supérieures. Pour une voix d'enfant, encore plus.
Attention : ces valeurs peuvent varier grandement en fonction de l'individu et au sein même du discours.
| Phonèmes en français | Ecriture phonologique (API) | Ecriture orthographique | Mot-clef | Formant F1 (Hz) | Formant F2 (Hz) | Formant F3 (Hz) | Bruit additionnel |
|---|---|---|---|---|---|---|---|
| Phonèmes à Formants : | |||||||
| Voyelles orales antérieures | |||||||
| /i/ | "i" | lit | 250 | 2250 | 3000 | ||
| /e/ | "é" | télé | 400 | 2050 | 2650 | ||
| /ε/ | "è" | règle | 600 | 1750 | 2600 | ||
| /a/ | "a" | sac | 750 | 1450 | 2600 | ||
| Voyelles orales centrales | |||||||
| /y/ | "u" | lune | 250 | 1750 | 2150 | ||
| /∂/ | "e" | ce | 550 | 1550 | 2550 | ||
| /ø/ | "eu" | feu | 350 | 1350 | 2250 | ||
| /œ/ | "oe" | fleur | 500 | 1350 | 2350 | ||
| Voyelles orales postérieures | |||||||
| /u/ | "ou" | poule | 300 | 750 | 2300 | ||
| /o/ | "au" | vélo | 350 | 750 | 2550 | ||
| /o ouvert à gauche/ | "o" | pomme | 500 | 1050 | 2550 | ||
| /α/ | "â" | pâte | 700 | 1250 | 2700 | ||
| Voyelles nasales | |||||||
| /œ tildé/ | "un" | un | 600 | 1350 | 2400 | ||
| /ε tildé/ | "in" | pain | 700 | 1500 | 2650 | ||
| /α tildé/ | "an" | gant | 750 | 1250 | 2400 | ||
| /o ouvert à gauche et tildé/ | "on" | ballon | 500 | 1250 | 2550 | ||
| Semi-voyelles ou Semi-consonnes | |||||||
| /j/ | "y" | fille | 250 | 2250 | 3000 | ||
| /u avec jambage à droite/ | "u+" | huit | 250 | 1750 | 2150 | ||
| /w/ | "w" | poisson | 300 | 750 | 2300 | ||
| Consonnes occlusives nasales | |||||||
| /m/ | "m" | mur | 300 | 1300 | 2300 | Explosion du "p" ou "b" | |
| /n/ | "n" | noeud | 350 | 1050 | 2300 | Explosion du "t" ou "d" | |
| /n avec jambage à gauche/ | "gn" | ligne | 350 | 1000 | 2400 | Explosion du "t" ou "d" | |
| /η/ | "nk/ng" | parking | 350 | 1050 | 2000 | Explosion du "k"/"g" | |
| Consonnes fricatives liquides | |||||||
| /l/ | "l" | lampe | 350 | 1700 | 2500 | Friction très faible | |
| /R renversé/ | "r" | roue | 550 | 1300 | 2300 | Friction très faible | |
| /R/ | "rrr" | terre | 550 | 1300 | 2300 | Friction très faible | |
| Phonèmes sans Formants : | |||||||
| Consonnes occlusives orales | |||||||
| /p/ | "p" | pile | Explosion moyenne, registre grave | ||||
| /b/ | "b" | bol | Explosion moyenne, registre grave | ||||
| /t/ | "t" | table | Explosion faible, registre aigu | ||||
| /d/ | "d" | dé | Explosion faible, registre aigu | ||||
| /k/ | "k" | cadeau | Explosion forte, registre medium | ||||
| /g/ | "g" | gâteau | Explosion forte, registre medium | ||||
| Consonnes fricatives non liquides | |||||||
| /f/ | "f" | flûte | Friction faible | ||||
| /v/ | "v" | valise | Friction faible | ||||
| /s/ | "s" | citron | Friction forte | ||||
| /z/ | "z" | maison | Friction forte | ||||
| /∫/ | "ch" | chat | Friction forte | ||||
| /3/ | "j" | jupe | Friction forte | ||||
| /h/ | "h aspiré" | hop | Friction forte | ||||
| /x/ | "J" | Juan Carlos | Friction forte |
Au niveau symbolisme phonétique, le Tableau ci-dessous résume les principales idées exprimées par chaque type de Phonèmes en français :
| Type de Phonèmes en français | Phonèmes | Symbolisme phonétique dans les langues primitives (cf [REDL pages 28-39]) | Symbolisme phonétique en français (cf [NOBI pages 141-149] en référence à [GRA 1933]) | Symbolisme phonétique en français (cf l'Auteur) |
|---|---|---|---|---|
| Voyelle | "i", "é", "è", "a" "u", "e", "eu", "oe" "ou", "au", "o", "â" "un", "in", "an", "on" | Visuel : sensation, passion, couleur, exclamation Auditif : son prolongeable, ton, inflexion de la Voix, Prosodie, poésie | "i" et "u" comme "aigu", "clair", ou comme dans "sifflé/flûté" "i", "é", "u", "eu", "è" comme "clair", "petit/ténu", "léger/subtil", "vif/subit" "a", "oe" et "o" comme "éclatant", "ouvert", "intense", "grand/gros", ou comme dans "craqué/croqué" "ou" et "au" comme "sombre", "lourd", "ombre", ou comme dans "gloussé" un", "in", "an", "on" comme "voilé" | VOYELLE = émotion, intonation Voyelle ouverte : "a", "â", "e", "oe", "è", "o" comme fort ou puissant Voyelle fermée palatale : "i", "é", "u", "eu" comme aigu ou perçant Voyelle fermée vélaire : "ou", "au", "on" comme sombre ou profond Voyelle nasale : "un", "in", "an" comme voilé ou doux |
| Semi-voyelle ou Semi-consonne | "y", "u+", "w" | Auditif : "y" = son mouillé | SEMI-VOYELLE comme la VOYELLE correspondante mais en plus bref "y", "u+" comme perçant "w" comme profond | |
| Consonne occlusive orale | "p", "b", "t", "d", "k", "g" | Mouvement sec ou saccadé | CONSONNES "p", "b", "t", "d", "k", "g" = explosé en une ou plusieurs fois | |
| labiale | "p", "b" | Visuel : mouvement des lèvres, baiser, amour, aménité, douceur | "p" et "b" comme "palpiter", "pétiller" | "p" et "b" = grave "p" et "b" comme posé ou palpité "pi", "py" comme piaillé |
| dentale | "t", "d" | Visuel : "t" et "d" = attachement, résistance, prétention Auditif : "t" comme "taper", "tinter", "tonner", "troubler", "tuer" | "t" comme "tousser", "tinter", "tituber", "trotter" | "t" et "d" = aigu "t" et "d" comme tranché ou tambouriné "tch", "tj" et "ts" comme tchatché "tch...k" et "tj...k" comme jacassé |
| vélaire | "k", "g" | Visuel : "k" et "g" = creux, profond, accumulé | "k" comme "casser", "crépiter" | "k" et "g" = fort "k" et "g" comme sec ou saccadé "kra", "krâ", "krw" comme croassé "gra", "grâ", "grw" comme croassé |
| Consonne occlusive nasale | "m", "n", "gn", "nk/ng" | Visuel : "m" et "n" = mouvement dedans/dehors et dehors/dedans Auditif : "gn" = son mouillé | "m", "n" et "gn" comme "mou", "nonchalant", "lent" | CONSONNES "m", "n" et "gn" = mou CONSONNE "nk/ng" comme la Consonne "k" ou "g" |
| Consonne fricative non spirante | "f", "v", "s", "z", "ch", "j", "h aspiré", "J" | Souffle | CONSONNES "f", "v", "s", "z", "ch", "j" = soufflé | |
| fuyante | "f", "v" | Visuel : mouvement des lèvres, baiser, amour, aménité, douceur Auditif : "f" comme "fuir", "v" comme "vent" | "f" comme "souffler", "siffler" et "v" comme "venter" "fl" comme "flotter", "flûter" et "fr" comme "frotter", "frôler", "froisser" | "f" et "v" = fuyante "f" et "v" comme fuyant, volant |
| sifflante | "s", "z" | Visuel : mouvement rapide dans l'air Auditif : "s" et "z" comme "siffler" | "s" comme "siffler", "souffler" | "s" et "z" = sifflante "s" et "z" comme sifflé, zozoté |
| chuintante | "ch", "j" | Visuel : mouvement léger et gracieux, douceur, plaisir Auditif : "ch" et "j" comme "chuinter", "chuchoter" | "ch" et "j" comme "chuchoter", "gémir" | "ch" et "j" = chuintante "ch" et "j" comme chuinté, gémi |
| glottale | "h aspiré" | CONSONNE "h" = expiré "h" comme hurlé, haleté, ahané "hou" comme hululé | ||
| vélaire | "J" | CONSONNE "J" comme la Consonne "r" | ||
| Consonne fricative liquide latérale | "l" | Visuel : mouvement rapide | Liquidité, "l" comme "lisse" "l" comme dans "claquer", "couler", "glisser", "filer", "voler" | CONSONNE "l" = lisse, coulant "...li", "...ly", "...lé" comme glissé, fluide "...lu", "...leu" comme flûté, pleuré "...la", "...lâ", "...le", "...lè", "...lo" comme claqué, lâché "...lou", "...lw", "...lau", "...lon" comme gloussé, plongé "...lin", "...lan" comme gloussé |
| Consonne fricative liquide vibrante | "r" | Visuel : mouvement rapide, "r" = roue, rotation | Vibration, "r" comme "rugueux" "ri" et "ru" comme dans "grincer", "briser", "vibrer", "crisser", "griller", "frire", "frémir" "ra", "re" et "ro" comme dans "râper", "racler", "branler", "trembler", "craquer", "écraser", "gratter", "fracasser" "rou" et "rau" comme dans "gronder", "ronfler", "bourdonner", "rauque", "grogner" | CONSONNE "r" = rugueux, rauque "...ri", "...ry", "...ré", "...ru", "...reu" comme grincé, crissé, grillé, vrillé, frémi "...ra", "...râ", "...rè" comme râpeux, braillé, craqué, gratté "...re", "...ro", "...rw" comme grogné, grondé, aigrelet, frôlé, frotté "...rou", "...rw", "...rau" comme roucoulé, roulé "...ron" comme ronronné, vrombi "...rin", "...ran" comme étranglé, branlé, tremblé |
Dans la musique occidentale, le Phrasé désigne la façon d'exécuter les différentes Phrases musicales d'un morceau musical, laquelle consiste essentiellement dans l'observation et le rendu de la ponctuation musicale, c'est-à-dire le Rythme (en particulier les éventuels Silences entre Phrases musicales), les Liaisons d'expression et le Phrasé en Notes détachées (Staccato).
Dans le chant, l'art du Phrasé (interprétation vocale) est lié essentiellement à la respiration, souvent indiquée dans le livret de chant par une virgule (voir Tempo).
Une Phrase grammaticale est une succession de Mots placés dans un ordre logique afin d'avoir un sens et de permettre d'exprimer une action ou un état.
Exemple : "Je crois que mon frère a une nouvelle amie."

Une Phrase musicale est une partie d'une Ligne mélodique naturellement délimitée, significative du point de vue de la déclamation, de l'articulation et de la respiration.
Les Phrases musicales sont composées généralement de quatre, voire huit Mesures.
La Figure ci-dessus donne l'exemple du début de la chanson "Au clair de la lune" pour lequel il y a quatre Phrases de quatre Mesures chacune, une Phrase par Portée. La Forme musicale est de type A A B A (Sonate).
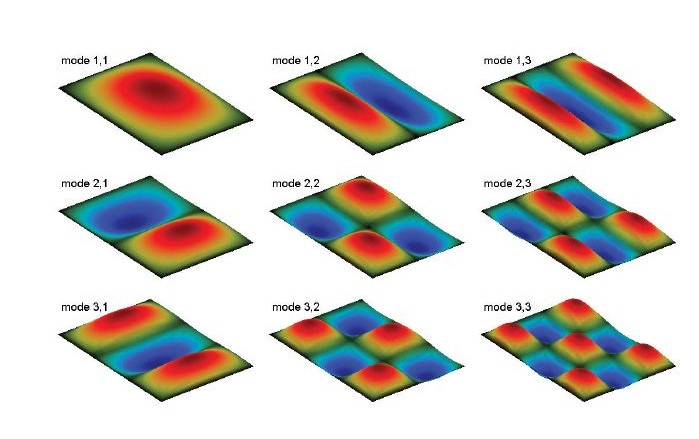

Figures 1 ci-dessus : les premiers modes propres d'une plaque mince rectangulaire à bords posés, avec exemple de lames de xylophone.
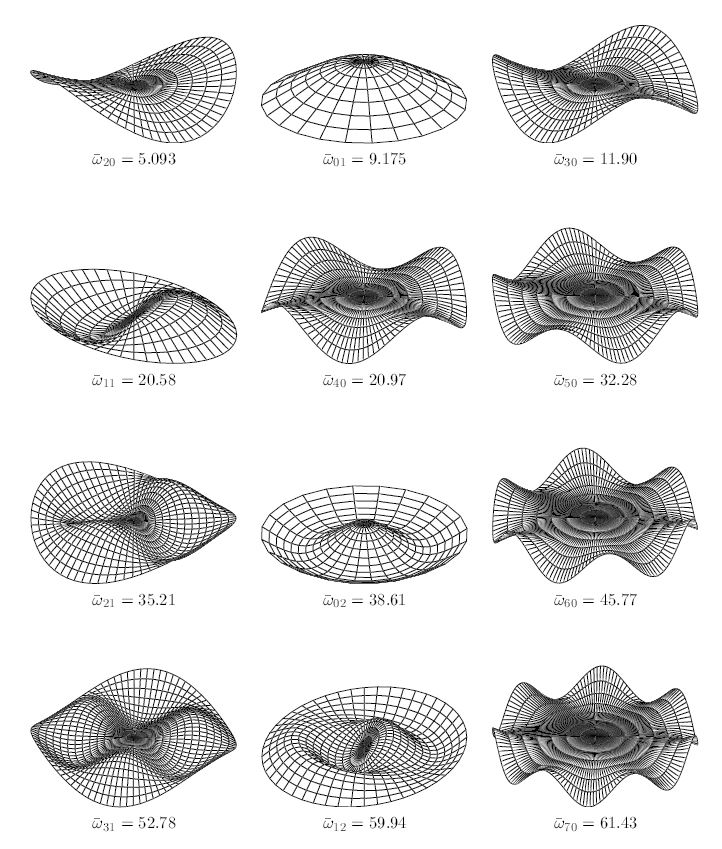
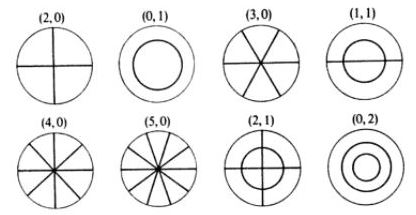

Figures 2 ci-dessus : les premiers modes propres d'une plaque mince circulaire à bord libre et maintenue en son centre, avec exemple de cymbales de batterie.
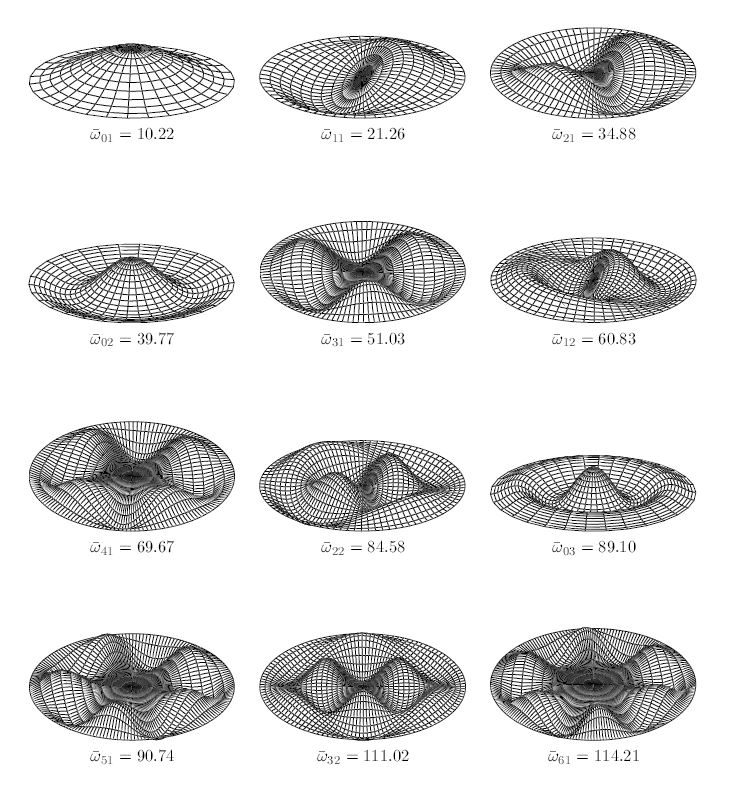

Figures 3 ci-dessus : les premiers modes propres d'une plaque mince circulaire à bord encastré, avec exemple de steel-drum. La Figure centrale s'applique également à la plaque mince circulaire à bord simplement posé.
Les plaques sont les équivalents en deux dimensions des poutres en flexion.
Généralités (communes avec Membrane vibrante) :
- Le son émis par une plaque ou une membrane vibrante, bien que constitué de Fréquences fixes, est un son complexe non périodique et ne se décompose pas en Séries de Fourier sous forme d'une somme d'ondes sinusoïdales dont les Fréquences sont des multiples entiers d'une même Fréquence Fondamentale. Les différentes Fréquences propres, dues aux différents Modes propres, peuvent cependant s'approcher plus ou moins bien d'une série Harmonique (cf [KAC]).
- Le Mode propre est défini par un couple (m ≥ 0, n ≥ 0), m et n étant des entiers.
- Les lignes nodales sont l'analogue en deux dimensions des noeuds des Cordes vibrantes.
- Les Modes propres sont dits "dégénérés" lorsque deux ou plusieurs couples (m, n) différents correspondent à la même Fréquence propre fmn. Ces Modes se superposent toujours, la linéarité de l'équation de la vibration transversale (équation d'onde) autorisant la superposition des solutions. Le système nodal est alors fonction des conditions initiales (à t = 0) imposées à la plaque ou à la membrane (cf [NICO, p.94]). A noter que chacun de ces Modes peut exister seul si les conditions initiales s'y prêtent (cf [LAME, p.133]).
Cas des plaques minces :
Pour tout type de plaque mince, le matériau est caractérisé par les constantes D et M suivantes :
D = raideur de flexion (en N.m) = E h3 / (12 (1 - ν2)) avec E = module de Young, h = épaisseur de la plaque et ν = coefficient de Poisson (généralement compris entre 0.2 et 0.4)
M = masse surfacique (en kg/m2) = ρ h avec ρ = masse volumique (en kg/m3)
L'équation de la vibration transversale se résoud mathématiquement lorsque le contour de la plaque est simple (rectangle, carré, cercle, ellipse, triangle, etc.) et en fonction des conditions limites (bords libres, bords simplement posés, bords encastrés, ou certaines combinaisons de ces trois cas sur l'ensemble des bords). Pour tous ces cas simples, [LEISSA] a donné les solutions sous forme analytique. Les cas usuels sont les suivants :
Plaque mince rectangulaire de côtés Lx et Ly, à bords posés (lame de xylophone par exemple) :
La Figure 1 ci-dessus donne les 9 premiers Modes propres d'une plaque rectangulaire supportée sur ses quatre bords, pour un rapport Ly/Lx non mentionné par l'auteur (cf [UPMC, p.101]).
Fréquences propres (cf [LEISSA, p.44] [PASC, p.43] [NICO, p.112] [ELIE, p.56] [MATTEI, p.43] [UPMC, p.100]) : fmn = (π/2) (D/M)1/2 ((m / Lx)2 + (n / Ly)2)
Le Mode propre est défini par le couple (m ≥ 1, n ≥ 1), m et n étant respectivement le nombre de ventres selon Ly et Lx.
Le mode fondamental est le mode (1, 1) pour lequel les seules lignes nodales sont sur les bords.
L'article [YUAN, Table 6 p.124] donne les 6 premiers Modes propres d'une plaque mince rectangulaire supportée sur ses quatre bords, en fonction de leur Fréquence propre et du rapport r = Ly/Lx. Pour le cas r = 2, la numérotation des Modes est a priori la suivante : (1, 1) (1, 2) (1, 3) (2, 1) (2, 2) (1, 4)
Modes propres dégénérés (cf [NICO, p.93]) : n'existent que dans le cas où le rapport Ly2/Lx2 est un nombre entier ou fractionnaire (cas de rapport commensurable). Exemple de fmn pour Ly2/Lx2 = 4 : f14 = f22 (voir [YUAN, p.124, Table 6, r = 2, modes 5 et 6]).
Déplacement transversal de la plaque (cf [LEISSA, p.44] [PASC, p.43] [UPMC, p.112]) : z(x, y, t) = ∑m≥1, n≥1[ (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) sin( m π x / Lx) sin( n π y / Ly) ]
Amn et Bmn = constantes déterminées par les conditions initiales de la plaque (à t = 0).
Plaque mince circulaire de rayon R, à bord libre et maintenue en son centre (cymbale par exemple) :
La Figure 2 ci-dessus donne, pour un coeffficient de Poisson valant 0.38, les premiers Modes propres d'une plaque circulaire à bord libre et maintenue en son centre, classés par Fréquences propres croissantes (cf [THOM, p.93] [FLETCH, p.78]).
Fréquences propres (cf [THOM, p.94] [FLETCH, p.78] [LEISSA, p.11]) : fmn = (1/(2π)) (D/M)1/2 (1/R)2 χmn
Le Mode propre est défini par le couple (m ≥ 0, n ≥ 0), hormis les couples (0, 0) et (1, 0), m étant le nombre de diamètres et n le nombre de cercles concentriques (hors circonférence qui n'est jamais une ligne nodale).
χmn = constante caractéristique du Mode propre et dépendant du coefficient de Poisson ν
Dans le cas où ν = 0.38, on a pour chaque m et n (cf [THOM, p.93] [ARAG, p.27] [RAUS, pp 10 et 44]) :
χ0(n ≥ 1) = 9.175 ; 38.61 ; etc.
χ1(n ≥ 1) = 20.58 ; 59.94 ; etc.
χ2(n ≥ 0) = 5.093 ; 35.21 ; etc.
χ3(n ≥ 0) = 11.90 ; 52.78 ; etc.
χ4(n ≥ 0) = 20.97 ; etc.
χ5(n ≥ 0) = 32.28 ; etc.
χ6(n ≥ 0) = 45.77 ; etc.
χ7(n ≥ 0) = 61.43 ; etc.
Dans le cas où ν est différent, les valeurs de χmn sont légèrement différentes : voir [LEISSA, p.11 avec les correspondances m = nLEISSA et n = sLEISSA] pour ν = 0.25 et 0.33, [CAM, p.6] pour ν = 0.33, [FLETCH, p.78 avec la correspondance χmn = (2 π 121/2) χmn FLETCH] pour ν = 0.30
Le mode fondamental est le mode (2, 0) de Fréquence propre f20 pour lequel les seules lignes nodales sont deux diamètres perpendiculaires.
Modes propres dégénérés : aucun a priori.
Fréquences propres approchées (cf [ROSS]) : fmn approximativement proportionnelles à la quantité (m + b n)k où b et k sont des constantes. Dans le cas d'une plaque circulaire plate (gong par exemple), b et k valent 2 conformément à la loi de Chladni (cf [CHLADNI, p.186] [ROSS]).
Déplacement transversal de la plaque en coordonnées polaires r et θ (cf [THOM, p.94] [FLETCH, p.78] [LEISSA, pp 2 et 7]) : z(r, θ, t) = ∑m≥0, n≥0 hormis_couples_(0, 0)_et_(1, 0)[ (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) Rmn(r) (Cmn sin(m θ) + Dmn cos(m θ)) ]
Rmn(r) = fonction dépendant des entiers m et n, et du coefficient de Poisson ν (voir [THOM, p.94])
Amn, Bmn, Cmn et Dmn = constantes déterminées par les conditions initiales de la plaque (à t = 0).
Plaque mince circulaire de rayon R, à bord encastré (steel-drum par exemple) :
La Figure 3 ci-dessus donne les premiers Modes propres d'une plaque circulaire à bord encastré, classés par Fréquences propres croissantes (cf [THOM, p.96] [FLETCH, p.78]).
Fréquences propres (cf [THOM, p.95] [FLETCH, p.78] [LEISSA, p.8]) : fmn = (1/(2π)) (D/M)1/2 (1/R)2 χmn
Le Mode propre est défini par le couple (m ≥ 0, n ≥ 1), m étant le nombre de diamètres et n le nombre de cercles concentriques (comprenant le bord).
χmn = constante caractéristique du Mode propre (indépendant du coefficient de Poisson ν), selon les valeurs suivantes (cf [THOM, p.96] [LEISSA, p.8 avec les correspondances m = nLEISSA et n = sLEISSA + 1] [FLETCH, p.78 avec la correspondance χmn = (2 π 121/2) χmn FLETCH]) :
χ0(n ≥ 1) = 10.22 ; 39.77 ; 89.10 ; etc.
χ1(n ≥ 1) = 21.26 ; 60.83 ; etc.
χ2(n ≥ 1) = 34.88 ; 84.58 ; etc.
χ3(n ≥ 1) = 51.03 ; 111.02 ; etc.
χ4(n ≥ 1) = 69.67 ; etc.
χ5(n ≥ 1) = 90.74 ; etc.
χ6(n ≥ 1) = 114.21 ; etc.
Le mode fondamental est le mode (0, 1) de Fréquence propre f01 pour lequel la seule ligne nodale est le bord lui-même.
Modes propres dégénérés : aucun a priori.
Déplacement transversal de la plaque en coordonnées polaires r et θ (cf [THOM, p.95] [FLETCH, p.78] [LEISSA, pp 2 et 7] ) : z(r, θ, t) = ∑m≥0, n≥1[ (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) Smn(r) (Cmn sin(m θ) + Dmn cos(m θ)) ]
Smn(r) = fonction dépendant des entiers m et n (voir [THOM, p.95])
Amn, Bmn, Cmn et Dmn = constantes déterminées par les conditions initiales de la plaque (à t = 0).
Plaque mince circulaire de rayon R, à bord simplement posé :
La Figure 3 centrale ci-dessus donne, pour un coeffficient de Poisson valant 0.30, les premiers Modes propres d'une plaque circulaire à bord simplement posé (cf [FLETCH, p.79]).
Fréquences propres (cf [FLETCH, p.79] [LEISSA, p.9]) : fmn = (1/(2π)) (D/M)1/2 (1/R)2 χmn
Le Mode propre est défini par le couple (m ≥ 0, n ≥ 1), m étant le nombre de diamètres et n le nombre de cercles concentriques (comprenant le bord).
χmn = constante caractéristique du Mode propre et dépendant du coefficient de Poisson ν
Dans le cas où ν = 0.30, on a pour chaque m et n (cf [FLETCH, p.79 avec la correspondance χmn = (2 π 121/2) χmn FLETCH] [LEISSA, p.9 avec les correspondances m = nLEISSA et n = sLEISSA + 1]) :
χ0(n ≥ 1) = 4.98 ; 29.77 ; 74.22 ; etc.
χ1(n ≥ 1) = 13.94 ; 48.53 ; 102.84 ; etc.
χ2(n ≥ 1) = 25.64 ; 70.14 ; 134.35 ; etc.
Le mode fondamental est le mode (0, 1) de Fréquence propre f01 pour lequel la seule ligne nodale est le bord lui-même.
Modes propres dégénérés : aucun a priori.
Déplacement transversal de la plaque en coordonnées polaires r et θ (cf [FLETCH, p.78] [LEISSA, pp 2 et 7] ) : z(r, θ, t) = ∑m≥0, n≥1[ (Amn sin(2 π fmn t) + Bmn cos(2 π fmn t)) Smn(r) (Cmn sin(m θ) + Dmn cos(m θ)) ]
Smn(r) = fonction dépendant des entiers m et n
Amn, Bmn, Cmn et Dmn = constantes déterminées par les conditions initiales de la plaque (à t = 0).
Voir Figure de Silence.
Voir Figure de Note et Figure de Silence.
Voir Figure de Note et Figure de Silence.



En notation musicale, la Portée est un ensemble de cinq Lignes horizontales et de quatre interlignes (voir Figure 1 ci-dessus) permettant de représenter les Clefs, les Figures de Note, les Figures de Silence, les Altérations, les Barres de Mesure et divers autres symboles complémentaires.
Des lignes supplémentaires sont souvent rajoutées pour étendre la Portée. Quand elles sont trop nombreuses, on emploie les symboles suivants (voir Figure 2 ci-dessus) :
- Sur la Portée en Clef de sol : symboles "8va" (ottava alta) et "15ma" (quindicesima alta) indiquant de jouer respectivement un ou deux Octaves au-dessus,
- Sur la Portée en Clef de fa : symboles "8ba" (ottava bassa) et "15mb" (quindicesima bassa) indiquant de jouer respectivement un ou deux Octaves au-dessous.
On appelle Système un ensemble de deux Portées ou plus, liées à leur gauche par une Barre de Système (voir Figure 1 ci-dessus).
L'Accolade permet de regrouper différentes Voix du même Instrument.
Le Crochet permet de regrouper des Instruments différents mais de la même Famille.


La Position d'un Accord est le mode de répartition des Notes de cet Accord, sans tenir compte généralement de la Basse (cf [FAB Unité 1.1]).
La Position peut être Ouverte (ou large ou espacée) ou Fermée (ou serrée) selon que les Notes sont plus ou moins espacées entre elles.
La Figure ci-dessus montre l'exemple de la réalisation à quatre Voix (Basse, Ténor, Alto, Soprano) d'un Accord de trois notes (cf [FAB Unité 1.1]). Les Notes Doublées sont indiquées en bleu (Fondamentale do). Pour cet Accord de do Majeur à l'Etat Fondamental (do - mi - sol), il n'existe que 6 Positions possibles : 3 Fermées (Figure de gauche) et 3 Ouvertes (Figure de droite).
Notes inférieures : le statut Basse-Ténor n'affecte pas la Position de l'Accord. La Basse peut même se déplacer d'une Octave par rapport au Ténor (exemples : Unisson vs Octave ou Tierce vs Dixième).
Notes supérieures : l'Accord est dit en Position d'Octave, de Quinte ou de Tierce lorsque respectivement l'Octave de la Fondamentale, la Quinte ou la Tierce se trouve en partie supérieure de l'Accord.
Voir Ecartement entre Voix.
Voir Unisson.
Voir Résonance.
En Langage parlé, la Prosodie est un moyen pour un locuteur d'exprimer des intentions et des émotions en faisant varier la Fréquence Fondamentale F0 de ses cordes vocales (Intonation), le Niveau d'Intensité et la Durée des Sons lors de la production d'une Phrase.
Par exemple, une élévation non abrupte de F0 en fin de Phrase est perçue comme une marque interrogative.
La Prosodie se caractérise essentiellement par : l'Accent, le Ton, l'Intonation, la Pause, le Rythme d'élocution et le Débit d'élocution (ou Tempo).
La Psychoacoustique étudie les rapports entre les perceptions auditives de l'être humain et les Sons qui parviennent à ses oreilles.
Elle fait appel à l'Acoustique, qui étudie la nature et les propriétés des ondes sonores, à la Physiologie de l'audition, qui examine dans quelle mesure elles se transforment en influx nerveux, à la Psychologie et aux Sciences cognitives.
La Pulsation est la quantité ω (en radian/s) égale à 2 π fois la Fréquence f.
La Quarte est l'Intervalle qui sépare quatre Degrés consécutifs dans la Gamme diatonique.
La Quarte juste correspond à 2 Tons et 1 Demi-ton. Elle a pour rapport 4/3 quand elle est Pure (soit une largeur de 0,42 Octave = log2(4/3)). Exemple en do Majeur : do - fa.
La Quinte est l'Intervalle qui sépare cinq Degrés consécutifs dans la Gamme diatonique.
La Quinte juste correspond à 3 Tons et 1 Demi-ton. Elle a pour rapport 3/2 quand elle est Pure (soit une largeur de 0,58 Octave = log2(3/2)). Exemple en do Majeur : do - sol.
Voir Phonème (définition).

Un Intervalle simple est un Intervalle n'excédant pas l'étendue d'une Octave.
Un Intervalle redoublé est un Intervalle excédant l'étendue d'une Octave. Ainsi, une Seconde redoublée peut être une Neuvième à l'Octave ou une Seizième à deux Octaves (voir Figure ci-dessus).
Attention : Ne pas confondre avec la Doublure.
Tout Redoublement dans un Intervalle ou un Accord améliore sa Consonance car les Harmoniques de la Note redoublée (2f, 4f, 6f, 8f...) ne sont pas différentes de celles de la même Note non redoublée (f, 2f, 3f, 4f...), tout en supprimant les Harmoniques de rang impair susceptibles de Dissonance avec les autres Notes. Voir Consonance entre deux Sons musicaux.
Voir Tessiture.
Voir Tonalité.

Renversement d'un Intervalle
Le Renversement d'un Intervalle est l'inversion de l'ordre des Notes qui composent l'Intervalle, en transposant la Note grave à l'Octave supérieure, l'autre Note restant à sa place.
Par exemple, la Quarte est le Renversement de la Quinte, et inversement. L'Intervalle ascendant sol-do est ainsi le Renversement de l'Intervalle ascendant do-sol.
Consonance et Dissonance :
- Le Renversement d'un Intervalle Consonant est Consonant.
- Le Renversement d'un Intervalle Dissonant est Dissonant.
Renversement d'un Accord
Le Renversement d'un Accord est l'inversion de l'ordre des Notes qui composent l'Accord, en transposant la Note grave à l'Octave supérieure, les autres Notes restant à leur place.
Le Renversement est déterminé par la Note qui se retrouve en Basse.
Ainsi (voir Figure ci-dessus, la Fondamentale étant indiquée en couleur rouge), pour un Accord à l'état "Fondamental réduit" (exemple : 1er Accord do - mi - sol) :
- Un premier renversement est un Accord qui a sa Tierce à la Basse (exemple : 3ème Accord mi - sol - do).
- Un deuxième renversement est un Accord qui a sa Quinte à la Basse (exemple : 4ème Accord sol - do - mi).
- Un troisième renversement est un Accord qui a sa Septième à la Basse. Il s'agit d'un Accord d'au moins quatre notes (exemple : si - do - mi - sol).
- Un quatrième renversement est un Accord qui a sa Neuvième à la Basse. Il s'agit d'un Accord de cinq notes (exemple : ré - si - do - mi - sol).
Le Renversement correspond ainsi à tout état "non-fondamental", c'est-à-dire lorsque la Fondamentale de l'Accord n'est pas à la Basse.
Consonance et Dissonance :
- Le Renversement d'un Accord Consonant est généralement Consonant.
- Le Renversement d'un Accord Dissonant est généralement Dissonant.
Voir Répétition.





Pour les Temps ou Mesures à rejouer, on utilise les symboles suivants (voir Figures 1 et 2 ci-dessus) :
- le Temps répété (symbole = n barres épaisses obliques, et entourées de deux points si le Temps est constitué de plusieurs valeurs rythmiques), qui indique de rejouer le Temps précédent (le nombre de barres indiquant la valeur rythmique du Temps : une barre pour Noire ou Croche, deux barres pour Double croche, etc.),
- les Mesures répétées (symbole = n barres épaisses obliques et entourées de deux points), qui indique de rejouer les n Mesures précédentes.
Pour les sections ou morceaux à rejouer, on utilise les symboles suivants (voir Figures 3, 4 et 5 ci-dessus) :
- le Renvoi (symbole = S barré entre deux points), qui marque clairement le début de la section,
- le Coda (symbole = cercle barré d'une croix), qui marque clairement la fin de la section,
- le Fine (symbole = "Fine"), qui marque clairement la fin du morceau,
- le Da Capo (symbole = "D.C."), qui indique qu'il faut rejouer "à partir du début du morceau",
- le Da Capo al Fine (symbole = "D.C. al Fine"), qui indique qu'il faut rejouer "à partir du début du morceau jusqu'à la fin du morceau",
- le Da Capo al Coda (symbole = "D.C. al Coda"), qui indique qu'il faut rejouer "à partir du début du morceau jusqu'au premier Coda" puis sauter au second Coda,
- le Dal Segno (symbole = "D.S."), qui indique qu'il faut rejouer "à partir du dernier Renvoi",
- le Dal Segno al Fine (symbole = "D.S. al Fine"), qui indique qu'il faut rejouer "à partir du dernier Renvoi jusqu'à la fin du morceau",
- le Dal Segno al Coda (symbole = "D.S. al Coda"), qui indique qu'il faut rejouer "à partir du dernier Renvoi jusqu'au premier Coda" puis sauter au second Coda,
- la Variante (symbole = un nombre égal à 1, 2, 3, etc., couvrant une ou plusieurs Mesures), qui indique un numéro de variante permettant de jouer deux fois une section avec deux variantes de fin différentes.
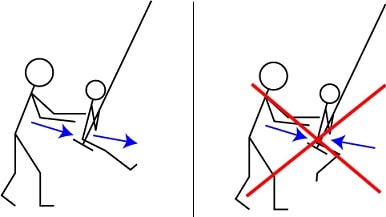
La résonance est une notion relative à des oscillations forcées. Les modes propres sont par contre relatifs à des oscillations libres (cf [THIE, p.27]).
Oscillation libre et Fréquence propre :
La Fréquence propre (ou naturelle) d'un système est la fréquence à laquelle il oscille librement après un déplacement initial, c'est-à-dire sans aucune force amplifiant ou réduisant son mouvement.
Par exemple, une balançoire légèrement poussée oscille naturellement selon une certaine fréquence propre et revient progressivement au repos à cause des frottements.
Oscillation forcée et Résonance :
La résonance est l'amplification de cette oscillation naturelle lorsqu'on fournit régulièrement au système de l'énergie à la même fréquence que sa fréquence propre.
Dans l'exemple de la balançoire, pour accentuer le mouvement il faut pousser au bon moment, et pas nécessairement trop fort (voir Figure ci-dessus).
Modes propres et modes de propagation (cf [THIE, pp 23-24]) :
Un mode d'un système physique est une solution des équations du mouvement, compatible avec les conditions aux limites, et dont la dépendance en temps est sinusoïdale.
Dans le cas de conditions aux limites imposées dans la direction de propagation, par exemple pour la Corde vibrante, les modes sont des ondes Stationnaires appelées modes propres ou modes normaux ou modes naturels.
En revanche, lorsque les conditions aux limites sont transverses à la direction de propagation, ce qui est le cas des guides d'ondes (par exemple pour le Tuyau sonore), les modes ont une structure mixte et conservent une partie progressive. Dans ce dernier cas, on parle plus simplement de modes, voire de modes de propagation.
Un système physique possède autant de modes qu'il a de degrés de liberté : un oscillateur masse-ressort a un mode propre, un système de deux pendules couplés en a deux, etc. Une Corde vibrante, en tant que système continu, possède une infinité de modes propres.
Remarque : La notion de mode est définie en régime libre. Nul besoin que les oscillations du système soient forcées.
Exemple de la Corde vibrante :
Dans le cas des oscillations forcées, toute onde Stationnaire met la corde en Résonance uniquement si l'interférence est constructive entre l'onde incidente et l'onde réfléchie, c'est-à-dire si les deux ondes sont en phase (cf [BOU Résonance]), ce qui revient à exciter la corde à une Fréquence égale à l'une de ses Fréquences propres (cf [THIE, p.27]).
Remarque : Les résultats sur les oscillations libres et ceux sur les oscillations forcées ne doivent pas être mélangés, la différence provenant des conditions de bord (au sens mathématique du terme) imposées à la corde. En effet (cf [THIE, p.27]) :
- dans le cas des oscillations libres, l'onde dépend de la donnée d'une condition initiale, c'est-à-dire y(x, t = 0) à un instant t unique et en tout point spatial x,
- dans le cas des oscillations forcées, l'onde dépend de la donnée d'une condition aux limites, c'est-à-dire y(x = 0, t) en un point spatial x unique et à tout instant t.
Voir Caisse de résonance.

La Réverbération d'un local clos est une caractéristique du local liée essentiellement à sa géométrie et à la nature de ses parois réfléchissantes.
Dans un tel local, le Son émis par une source sonore se trouve prolongé, après arrêt de la source, grâce aux multiples réflexions sur les parois du local. Sans phénomène de réverbération (écoute en espace libre), le Son direct ne serait perceptible qu'à courte distance de la source (voir Figure ci-dessus) car son énergie décroit avec la distance d comme 1/d2.
Le Temps de réverbération (Tr) d'un local est, par définition, la durée de décroissance d'un Son entre un Niveau d'Intensité quelconque et un Niveau d'Intensité plus faible de 60 dB.
La formule suivante (formule de Wallace Sabine) permet de calculer une bonne approximation de Tr pour un local donné ou, à l'inverse, de déterminer la nature de ses parois pour obtenir un Tr imposé.
Tr = k V / (α S)
avec :
Tr en secondes
k = 0,16 s/m
V et S = volume du local (en m3) et surface totale des parois (en m2)
α = coefficient d'absoption moyen du local = (1/S) ∑n[αn Sn]
αn et Sn = coefficient d'absorption (de 0 à 1) et surface (en m2) de la paroi n du local, que ce soit un mur, un plancher ou un plafond.
Ainsi, pour une pièce d'habitation normalement meublée (α = 0,2 environ) de dimensions (Longueur = 5 m) x (largeur = 4 m) x (Hauteur = 3 m), le Temps Tr vaut 0,16 x 60 / (0,2 x 2 (20 + 15 + 12)) = 0,5 s.
La Ronde est l'une des Figures de Note et aussi la base de calcul pour l'Unité de Temps de la Mesure.
En Langage parlé, le Rythme est un des composants de la Prosodie qui mesure la segmentation de la chaîne parlée en motifs répétitifs proéminents.
En français, le Rythme est donné par le nombre moyen de Syllabes prononcées par groupe de Mots, chaque groupe portant l'Accent tonique. Les Rythmes courants sont :
- le Rythme ternaire : Vous avez | certainement | répondu | qu'il viendrait | en voiture.
- le Rythme quaternaire : Vous avez dit | qu'il arriverait | mardi matin.
- le Rythme combinatoire 2 | 3 | 4 : Il dit | qu'il viendra | un peu plus tard.
En Musique, le Rythme est l'organisation temporelle des événements musicaux.
En notation musicale, le Rythme est caractérisé essentiellement par :
- les Durées (Figure de Note, Figure de Silence, Durée d'une Note, Durée d'un Silence, Liaison, Ornement),
- les Mesures (Barre de Mesure, Chiffrage de Mesure),
- les Répétitions de Temps, Mesures, sections ou morceaux,
- le Tempo,
- le Caractère,
- les Rythmes parfois Irrationnels.
La Seconde est l'Intervalle qui sépare deux Degrés consécutifs dans la Gamme diatonique.
La Seizième est l'Intervalle constitué d'une Seconde augmentée de deux Octaves justes. On parle aussi d'Intervalle "Redoublé à deux Octaves".
Voir Phonème.
Voir Degré.
La Septième est l'Intervalle qui sépare sept Degrés consécutifs dans la Gamme diatonique.
Le Silence est une interruption momentanée du Son dans l'exécution d'un morceau musical. Il est caractérisée par une Durée.
Une Sixte est l'Intervalle qui sépare six Degrés consécutifs dans la Gamme diatonique.
La Sixte majeure correspond à 4 Tons et 1 Demi-ton. Elle a pour rapport 5/3 quand elle est Pure (soit une largeur de 0,74 Octave = log2(5/3)). Exemple en do Majeur : do - la.
La Sixte majeure correspond aussi à la Tierce mineure Renversée qui est le complémentaire de la Tierce mineure dans l'Octave (5/3 x 6/5 = 2).
Une Sixte est l'Intervalle qui sépare six Degrés consécutifs dans la Gamme diatonique.
La Sixte mineure correspond à 3 Tons et 2 Demi-tons. Elle a pour rapport 8/5 quand elle est Pure (soit une largeur de 0,68 Octave = log2(8/5)). Exemple en do Majeur : mi - do.
La Sixte mineure correspond aussi à la Tierce majeure Renversée qui est le complémentaire de la Tierce majeure dans l'Octave (8/5 x 5/4 = 2).
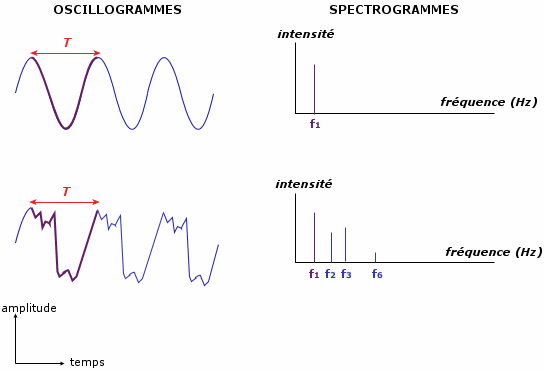
Un Son musical (voir Figure 2 ci-dessus) est une onde de pression acoustique qui varie périodiquement dans le temps (Période T), ce qui le distingue d'un Bruit ou d'une Percussion qui sont des Sons complexes non périodiques à Fréquences aléatoires pour le premier et à Fréquences fixes pour le second.
Un Son musical n'est pas forcément sinusoïdal comme l'est un Son pur.
Un Son musical est caractérisé par une Hauteur, une Intensité, une Durée et un Timbre.
Un Son musical est Décomposable en séries de Fourier.
Un Son pur (Voir Figure 1 ci-dessus) est un Son musical dont la pression acoustique p(t) est une fonction sinusoïdale de la forme :
p(t) = A sin (ω t + φ)
A est l'amplitude du signal (en Pascal ou N/m2), ω la Pulsation (en radian/seconde), t le temps (en seconde) et φ la phase (en radian).
Si f est la Fréquence, alors ω = 2 π f.
A noter : l'oreille est quasi-insensible à la phase.
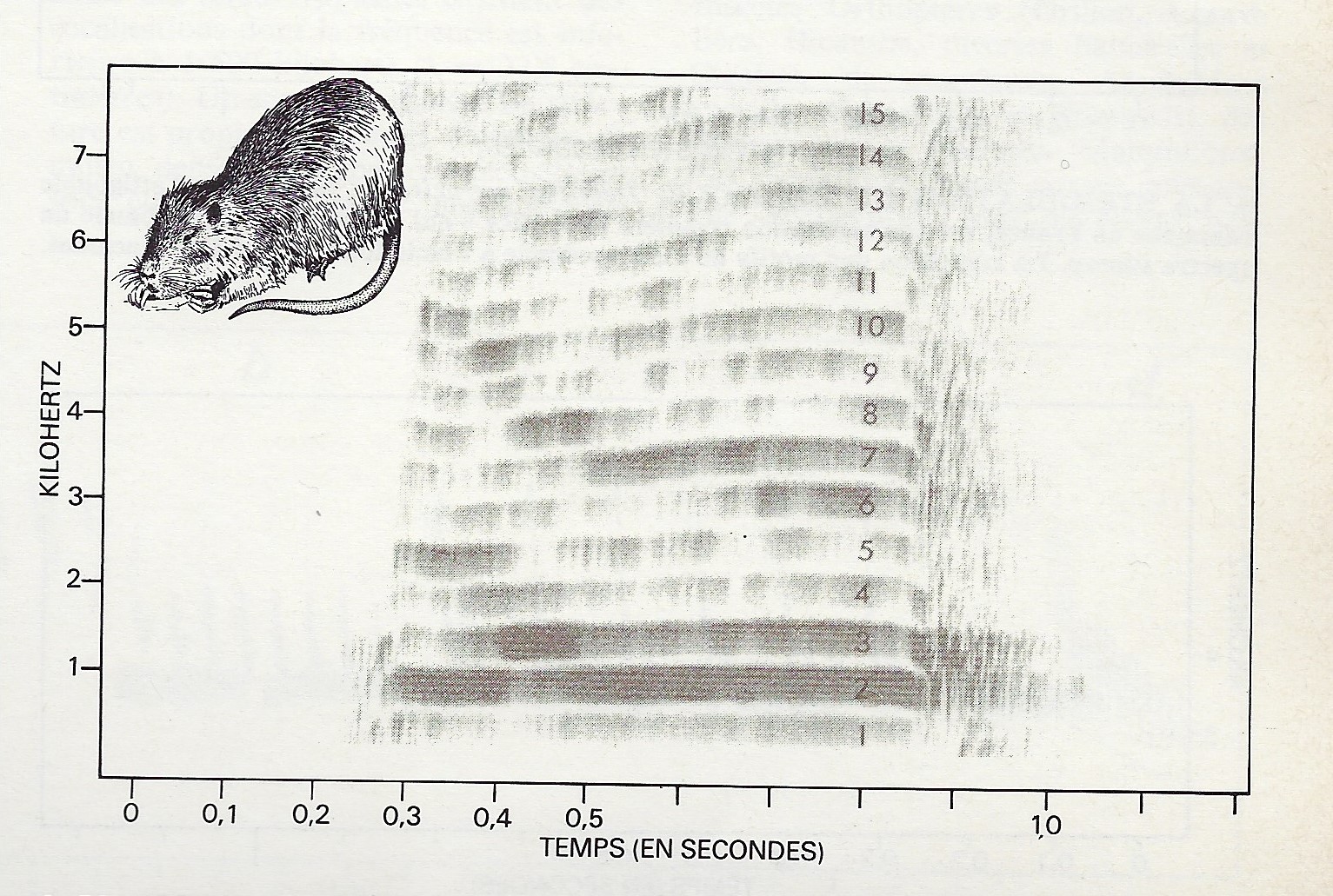
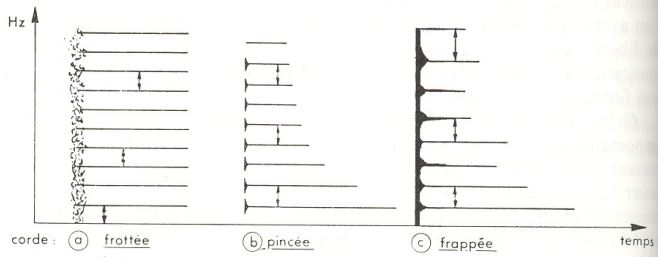

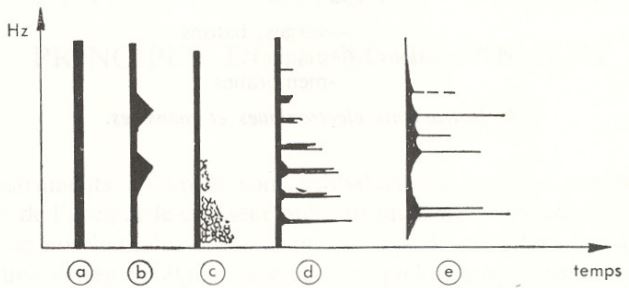
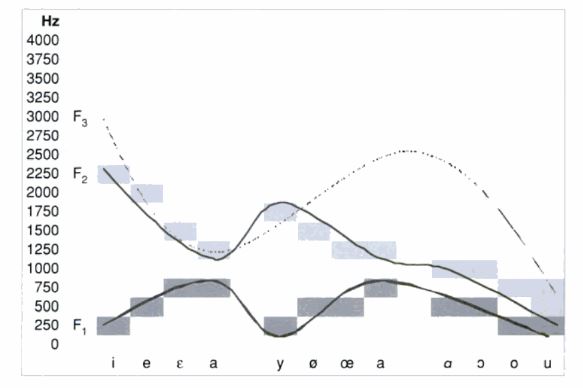
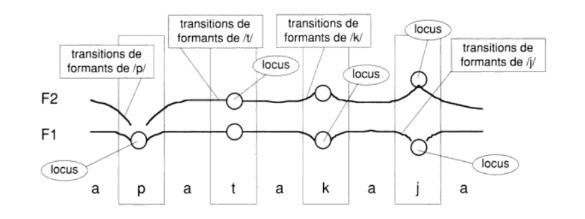
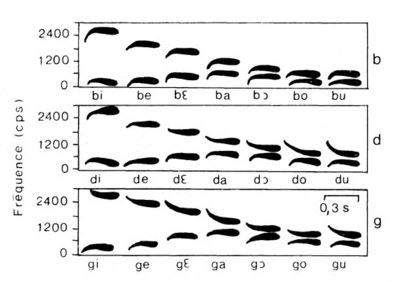
Le Sonagramme ou Sonogramme est la représentation graphique de l'évolution du Spectre sonore en fonction du temps.
Sur un Sonagramme, les Fréquences sont inscrites en ordonnée et le temps en abscisse (voir Figure 1 ci-dessus). La noirceur du trait de l'enregistrement sonore indique la valeur de l'Intensité sonore à une Fréquence donnée et à un temps donné.
Les traits fortement noircis correspondent aux Formants (ou Zones formantiques) qui sont des groupes d'Harmoniques voisins dont l'Intensité est renforcée par les Résonateurs associés au Vibrateur.
Les Formants contribuent au Timbre et évoluent en fonction du Temps. Ils sont habituellement numérotés F1, F2, F3, etc., en allant des basses Fréquences vers les hautes Fréquences. La notation F0 est réservée à la Fréquence Fondamentale.
Le Tableau ci-dessous donne des exemples de Sonagrammes pour le cri animal, les Instruments de musique et le Langage parlé.
| Sonagramme | Exemples |
|---|---|
| Cri animal |
La Figure 1 ci-dessus montre, en exemple de cri animal, le Sonagramme du ragondin (cf [LEROY, p.131]). On peut remarquer que : - Son cri est un Son harmonique avec un peu de Bruit à l'Attaque et surtout à la fin du cri (extinction). - La Fondamentale (première bande horizontale de la Figure à partir du bas, notée 1) est faible tandis que quelques Harmoniques sont plus intenses (2, 3, 6 et 7). - Au cours du Temps, la Fondamentale (1) et l'Harmonique (2) sont à peu près constants. - Pour l'Harmonique (3), il est d'abord faible pendant 0,1 seconde, passe par un maximum puis décroît et reste constant jusqu'à la fin du cri. |
| Instruments de musique |
Les Sonagrammes des Instruments de musique sont les suivants (cf [GAB Acoustique]) : Instruments à cordes (voir Figure 2 ci-dessus) : a) A cordes frottées (exemple : violon) : Les Sons étant entretenus par définition, le Spectre sonore est Harmonique, à raies équidistantes et à extinctions quasi-simultanées. L'Attaque est faiblement Bruitée. b) A cordes pincées à vibration libre (exemple: guitare) : Le Spectre sonore est quasi-Harmonique, à raies s'écartant très légèrement et à extinctions généralement plus courtes quand on va vers les aigus. L'Attaque est un petit trait vertical, indice du petit choc que produit la corde au moment où on l'abandonne. c) A cordes frappées à vibration libre (exemple : piano) : Le Spectre sonore est identique au cas précédent. Mais ici le choc de l'Attaque est beaucoup plus intense (trait vertical plus gros et plus large) avec des décalages dans les extinctions. Instruments à vent (Bois et Cuivres) (voir Figure 3 ci-dessus) : a) A biseau (exemple : flûte) : Les Sons étant entretenus par définition, le Spectre sonore est Harmonique, à raies équidistantes mais en nombre restreint. Les Harmoniques sont relativement intenses dans les graves et décroissant régulièrement en Intensité avec le rang. Le Spectre sonore est légèrement Bruité par le souffle, et avec un Son de bouche apparaissant avant le Son proprement dit. L'Attaque est graduelle avec des Harmoniques n'apparaissant pas simultanément. b) A anche libre, simple, double ou à anche lippale (exemple : trompette d'orgue) : Le Spectre sonore est identique au cas précédent mais avec des Harmoniques en plus grand nombre, sans être Bruités et sans décroître régulièrement en Intensité avec le rang. Les Formants sont très intenses. Instruments de percussion (voir Figure 4 ci-dessus) : Tous ces instruments se caractérisent par une Attaque brutale et intense, contenant tous les Harmoniques, qui se traduit par un gros trait vertical. Après le choc, le Sonagramme peut avoir diverses allures : a) Choc très amorti (sur du bois par exemple) : Le trait vertical est peu large. C'est le cas de la crécelle par exemple. b) Choc amorti sur un matériau offrant une ou deux Résonances (sur une Plaque composite en bois par exemple) : Le Son possède une certaine Hauteur mais la sensation reste floue. c) Choc bruyant avec une Résonance grave de Hauteur indéfinissable : C'est le cas du coup de tambour. d) Choc non amorti sur un corps à deux dimensions principales : Le Spectre sonore est vaguement Harmonique avec des extinctions non simultanées. C'est le cas des corps longs (exemples : tringle, tube en métal) ou minces (exemple : lame en fer). e) Choc non amorti sur un corps à trois dimensions comparables : Le Spectre sonore n'est pas du tout Harmonique. C'est le cas de la cloche ou d'un choc sur Plaque épaisse. |
| Langage parlé |
La Figure 5 ci-dessus (cf [MUNO] p.51) montre les Sonagrammes des principales Voyelles du français, dans l'ordre suivant (selon écriture orthographique) : "i", "é", "è", "a", "u", "eu", "oe", "a", "â", "o", "au", "ou". La Voyelle "e" et les Voyelles nasales ne sont pas représentées. Par ailleurs, deux Voyelles "a" font la distinction entre prononciations régionales (le premier "a" pour "la" et le second "a" pour "bas"). On peut remarquer que seuls les deux premiers Formants F1 et F2 sont très audibles et suffisent à identifier une Voyelle. Les autres Formants (à partir de F3) aident seulement à identifier la voix du locuteur. La Figure 6 ci-dessus (cf [MUNO] p.59) montre les Sonagrammes des Transitions de Formants des Consonnes "p", "t", "k" et "y" du français, prononcées avant et après la Voyelle "a". Ces Transitions sont les "mouvements" vers le haut ou vers le bas des Formants des Voyelles environnantes, avant et après dans la chaîne parlée. Le "locus" (représenté par un petit rond) est le lieu théorique de rencontre des Transitions formantiques concernant les Formants F1, F2 et F3 des Voyelles, et plus particulièment F2 (cf [SCOTTO]). Le locus propre à une Consonne donnée reste le même, quelle que soit la Voyelle suivante. La Figure 7 ci-dessus (cf [PETE] p.566) montre les Sonagrammes des Transitions de Formants des Consonnes "b", "d" et "g" du français, prononcées avant chaque Voyelle "i", "é", "è", "a", "o", "au", "ou", dans une Syllabe de type CV. La description générale des Formants relatifs aux Phonèmes en français est disponible dans Musique - Lexique - Phonèmes (définition). |
Voir Appareil vocal.
Voir Figure de Silence.
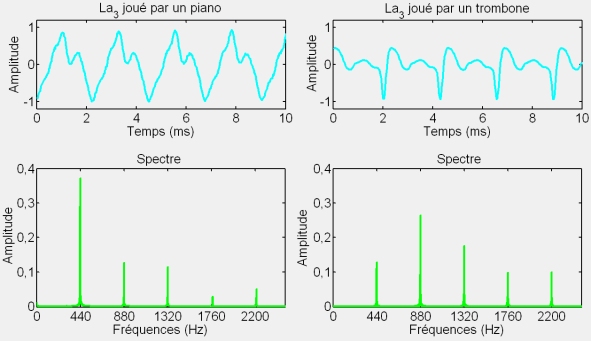
Le Spectre sonore est la représentation des Harmoniques d'un Son musical dans le domaine Intensité - Fréquence (voir Figure ci-dessus. Exemple du la3 joué par un piano et par un trombone).
Le Spectre sonore contribue fortement au Timbre.
Voir Figure de Note.

Une onde stationnaire est une onde dont les termes spatial (x) et temporel (t) sont découplés (cf [THIB], p.22].
Formellement, l'amplitude y(x, t) d'une onde plane stationnaire s'écrit : y(x, t) = f(x) g(t)
Au lieu de voir une onde qui se propage, on constate une vibration stationnaire mais d'amplitude différente, en chaque point observé (voir exemple en Figure ci-dessus). Les points fixes caractéristiques sont appelés des noeuds.
Dans un système physique, une onde est stationnaire uniquement dans le cas d'une oscillation forcée sinusoïdalement ou d'une condition initiale (à t = 0) ayant la forme d'un mode Propre (c'est-à-dire une sinusoïde) (cf [THIE, p.27]). Le second cas ne se produit jamais en pratique car il faudrait pouvoir déformer manuellement le système de cette façon.
Dans un Accord, une Note peut parfois être supprimée, par exemple, quand le nombre de Voix est insuffisant.
On supprime le plus souvent la Quinte juste d'un Accord, que l'on retrouve dans les Harmoniques de la Tonique.
Sauf exception, on ne supprime pas les Notes déterminantes de l'Accord, à savoir :
- sa Quinte lorsque elle est augmentée ou diminuée ;
- sa Fondamentale, qui donne la précision tonale ;
- sa Tierce, qui indique la qualité (Majeure ou Mineure) de l'Accord ;
- toute Note altérée.
Un Accord est dit Suspendu quand sa Tierce constitutive est omise, remplacée généralement par une Quarte juste ou, beaucoup plus rarement, par une Seconde.
Par exemple, l'Accord de do majeur do - mi - sol devient do - fa - sol (noté "sus4") dans le premier cas et do - ré - sol (noté "sus2") dans le second.
La tension entre la Quarte et la Quinte, ou entre la Seconde et la Basse fondamentale, crée une Dissonance.
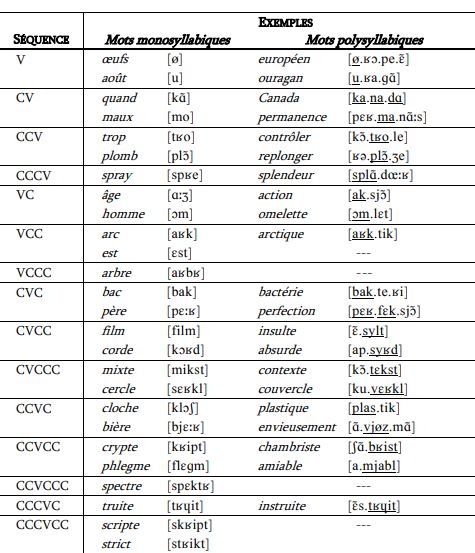
Une Syllabe orale est un Son ininterrompu du Langage parlé, prononcé en une seule émission de Voix. Le Mot "opérateur" par exemple comprend quatre Syllabes (o/pé/ra/teur).
En français, le noyau d'une Syllabe est toujours un Phonème de type Voyelle (V), entouré éventuellement de un ou plusieurs autres Phonèmes de type Consonne (C). Par exemple, le Mot monosyllabique "film" est une simple Syllabe du type CVCC comprenant quatre Phonèmes distincts (/f/ /i/ /l/ /m/).
Les Consonnes qui précédent la Voyelle constituent l'"Attaque". Celles qui la suivent constituent le "Coda".
Le français permet une grande variété de Syllabes qui peuvent contenir jusqu'à trois Consonnes devant la Voyelle et trois après (voir Figure ci-dessus, cf [STEE], les points "." indiquant les frontières entre Syllabes), à laquelle il faut rajouter la séquence CVCCCC avec "dextre" comme seul mot possible).
Les structures syllabiques les plus fréquentes sont les suivantes (avec V pour Voyelle et C pour Consonne) : CV, CVC, CCV, VC.
La découpe d'un Mot en Syllabes respecte habituellement deux principes (cf [STEE]) :
- Préférence nette pour les Syllabes à Consonne initiale, c'est-à-dire avec des Attaques. Par exemple, le Mot "entrevue" peut se découper théoriquement en "en/tre/vue", "en/trev/ue", "ent/re/vue", "ent/rev/ue", "entr/e/vue" ou "entr/ev/ue". On choisit toujours la découpe qui crée le plus grand nombre de Syllabes ayant une Attaque, soit les découpes "en/tre/vue" ou "ent/re/vue".
- Maximisation de l'Attaque. On groupe le plus de Consonnes possibles en début de Syllabe. La découpe qui convient est alors : "en/tre/vue".
A l'écrit, la découpe d'un Mot en Syllabes peut être différente. Le Mot "astre" par exemple est constitué de deux Syllabes écrites (as/tre) et d'une seule à l'oral.
Voir Phonème (symbolisme).

Le Tempo (en nombre de battements ou de Pulsations par minute - abréviation "bpm") fixe la durée exacte des Temps. Il est indiqué sur la partition pour un passage musical donné sous forme d'un terme de mouvement et/ou d'une indication métronomique. Exemples de progression entre lent et rapide :
Largo 40, Lento 60, Adagio ou adgo 70, Andante ou andte 90, Moderato ou modto 110, Allegretto ou allto 120, Allegro ou allo 130, Vivace 140, Presto 160, Prestissimo ou prestmo 200.
La Figure ci-dessus donne un exemple de Tempo "Adagio" où l'on doit jouer en une minute l'équivalent de 60 Croches, 30 Noires ou encore 15 Blanches.
Attention : Ne pas confondre Tempo et Nuance.
Au cours d'un morceau musical, le Tempo peut être modifié, soit par une nouvelle indication métronomique, soit par :
- un terme de ralentissement (exemples : Allargando ou allarg., Rallentando ou rall.),
- un terme d'accélération (exemples : Animato, Accelerando ou accel., Più moto),
- un terme de retour au Tempo initial (exemples : Tempo primo ou To Io, a tempo ou a To),
- un terme de suspension passagère d'une Note ou d'un Silence (voir Point d'orgue),
- un terme de suspension passagère d'un passage complet (exemples : ad libitum ou ad lib., Senza tempo),
- un terme de suspension passagère du Tempo (exemple : la "respiration" qui est une virgule placée au-dessus de la Portée).
Le Tempo peut aussi être "coloré" par certains termes de Caractère.
Le Temps en musique est la Période en secondes du mouvement oscillatoire du métronome fixé par le Tempo.
Voir détail dans Hauteur de Note.
Un Tétracorde est la succession ascendante ou descendante de quatre Notes Conjointes, par exemple : do ré mi fa.
Le Tableau ci-dessous donne la liste des principaux Tétracordes :
| Tétracorde | Nom | Note | Note | Note | Note | |||
|---|---|---|---|---|---|---|---|---|
| à Quarte juste | Majeur ou Ionien | Ton | Ton | 1/2 Ton | ||||
| à Quarte juste | Mineur ou Dorien | Ton | 1/2 Ton | Ton | ||||
| à Quarte juste | Phrygien | 1/2 Ton | Ton | Ton | ||||
| à Quarte juste | Sesqui ou Blues | 3/2 Ton | 1/2 Ton | 1/2 Ton | ||||
| à Quarte juste | Harmonique | 1/2 Ton | 3/2 Ton | 1/2 Ton | ||||
| à Quarte juste | Inconnu | 1/2 Ton | 1/2 Ton | 3/2 Ton | ||||
| à Quarte augmentée | Lydien | Ton | Ton | Ton | ||||
| à Quarte augmentée | Hongrois majeur | 1/2 Ton | 3/2 Ton | Ton | ||||
| à Quarte augmentée | Hongrois mineur | Ton | 1/2 Ton | 3/2 Ton | ||||
| à Quarte diminuée | Phrygien espagnol | 1/2 Ton | Ton | 1/2 Ton |
Une Tierce est l'Intervalle qui sépare trois Degrés consécutifs dans la Gamme diatonique.
La Tierce majeure correspond à 2 Tons. Elle a pour rapport 5/4 quand elle est Pure (soit une largeur de 0,32 Octave = log2(5/4)). Exemple en do Majeur : do - mi.
Une Tierce est l'Intervalle qui sépare trois Degrés consécutifs dans la Gamme diatonique.
La Tierce mineure correspond à 1 Ton et 1 Demi-ton. Elle a pour rapport 6/5 quand elle est Pure (soit une largeur de 0,26 Octave = log2(6/5)). Exemple en do Majeur : mi - sol.
Le Timbre est l'ensemble de caractéristiques d'un Son musical produites par ses Harmoniques (Spectre sonore, Attaque, Brillance, Formants, Vibrato, etc.).
Le Timbre permet d'identifier un Instrument de façon unique.
Le Titre d'une oeuvre musicale est généralement de la forme suivante (cf [GRDM]) :
Titre = Genre Instrument Ordre Tonalité , Opus , Catalogue (Date) , "Titre_secondaire" , Compositeur
Exemples de titre complet :
- Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
- Symphonie n°41 en ut majeur, KV 551 (1788), dite "Jupiter" de Wolfgang Amadeus Mozart
- Die junge Nonne, D 828 (1825), de Franz Schubert, arr. Franz Liszt (S 558, n° 6, 1837-1838)
Genre et Instrument donne la nature de l'oeuvre, donnée par le compositeur.
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
L'Ordre indique la place de l'oeuvre dans l'ensemble des oeuvres du compositeur de même nature (Genre et Instrument).
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
Le numéro d'ordre peut parfois se trouver juste derrière le Genre, auquel cas il est relatif seulement au Genre, quel que soit l'Instrument.
Ainsi, "Sonate n°3 pour piano et violon" signifie qu'il s'agit de la 3ème sonate écrite par le compositeur, quel que soit le type d'Instrument pour lequel cette sonate a été écrite, tandis que "Sonate pour piano et violon n°3" signifie qu'il s'agit de la 3ème sonate du compositeur écrite pour ces deux Instruments.
Attention : Ne pas confondre le numéro d'ordre avec le numéro d'Opus ou son numéro de composition ou le numéro de l'oeuvre dans le Catalogue.
La Tonalité n'est pas toujours la Tonalité d'origine mais une Tonalité transposée, ce qui est souvent le cas des éditions pratiques des oeuvres des grands compositeurs romantiques comme Schubert, Schumann et Brahms, dont il existe des éditions pour Voix aigües et graves.
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
L'Opus indique la place de l'oeuvre dans l'ensemble des oeuvres du compositeur. L'Opus est toujours précédé d'une virgule.
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
Le Catalogue est spécifique d'un éditeur et regroupe l'ensemble des oeuvres d'un même compositeur. Le Catalogue est toujours précédé d'une virgule.
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
Une même oeuvre peut être référencée dans plusieurs Catalogues.
Ainsi, le "Concerto pour clavecin et orchestre à cordes en fa mineur" de Johann Christian Bach est référencé "W 73" dans le Catalogue Ernest Warburton et "T 301/4" dans le Catalogue Charles Sanford Terry.
La Date est généralement l'année de fin d'écriture de l'oeuvre ou un intervalle de dates reflétant la durée du processus créateur.
La Date se place entre parenthèses, indifféremment après l'Opus ou après le Catalogue.
Exemple : Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740), de Georg Friedrich Haendel
L'année de révision de l'oeuvre peut être éventuellement précisée (sigle "révision"), ainsi que l'année de publication lorsqu'elle diffère de l'année de composition (sigle "publ."), ainsi que l'année de première représentation dans le cas des opéras (sigle "créé en").
Exemple 1 : Héroïde funèbre, S 102 (1849-1850, révision 1854-1856), de Franz Liszt
Exemple 2 : Lieder und Gesänge, op. 27 (1840, publ. 1849), de Robert Schumann
Exemple 3 : Der Schatzgräber (créé en 1920), de Franz Schreker
Le Titre secondaire est un surnom de l'oeuvre consacré par l'usage. Il est toujours précédé d'une virgule, placé entre guillemets précédés parfois du sigle "dit(e)".
Exemple : Symphonie n°41 en ut majeur, KV 551 (1788), dite "Jupiter", de Wolfgang Amadeus Mozart
Le Compositeur est toujours précédé d'une virgule. Il est parfois suivi du nom d'un autre Compositeur ayant arrangé l'oeuvre d'origine (sigle "arr.").
Exemple : Die junge Nonne, D 828 (1825), de Franz Schubert, arr. Franz Liszt (S 558, n° 6, 1837-1838)
Dans une liste d'oeuvres musicales, le Compositeur est souvent placé en début de Titre.
Exemple : Georg Friedrich Haendel, Concerto pour orgue n°8 en la majeur, op. 7 n°2, HWV 307 (1740).

Le Ton comme Intervalle est le plus grand des Intervalles Conjoints de la Gamme diatonique. Il est égal à la somme d'un Demi-ton chromatique et d'un Demi-ton diatonique. Exemple : (do - ré) = (do - do#) + (do# - ré).
En Gamme de Pythagore, on a :
1 Ton (rapport 9/8) = 1 Demi-ton chromatique (rapport 37/211) + 1 Demi-ton diatonique (rapport 28/35)
En Gamme de Zarlino, on a :
1 Ton mineur (10/9) = 1 petit chromate (25/24) + 1 petit diaton (16/15)
1 Ton majeur (9/8) = 1 petit chromate (25/24) + 1 grand diaton (27/25) = 1 grand chromate (135/128) + 1 petit diaton (16/15)
En Gamme tempérée, on a :
1 Ton (22/12) = 1 Demi-ton chromatique (21/12) + 1 Demi-ton diatonique (21/12)
Les musiciens considèrent généralement (voir exemple en Figure ci-dessus cf [DAN]) qu'un Ton vaut (n = 9) Commas. Il s'agit implicitement du Comma pythagoricien pour lequel on a :
Comma pythagoricien : 1,0136 correspondant à l'Intervalle entre 12 Quintes et 7 Octaves (soit (3/2)12/27)
Ton (9/8) = environ (1,0136)n
En Langage parlé, le Ton est un des composants de la Prosodie qui permet de changer la signification d'un Mot, soit en modifiant l'Intonation de certaines Syllabes par rapport aux autres (Ton ponctuel), soit en modifiant leur Mélodie (Ton mélodique). Exemples (cf [MARTINET, Eléments, pp 86, 87]) :
- Ton ponctuel : en Lonkundo (une des langues du Congo), le Mot qui désigne le fruit du palmier se prononce lo.ko.lo avec un Ton égal sur les trois Syllabes. Celui qui désigne le terme "exorcisme" se prononce avec un Ton plus haut sur les deux dernières Syllabes.
- Ton mélodique : en suédois, le Mot qui désigne la virgule se prononce komma selon un Ton unique (montante ou descendante selon les dialectes) et celui qui désigne le verbe "venir" avec un Ton descendant puis montant.
La plupart des langues du Monde sont tonales et presque toutes non-européennes (exemples : chinois, vietnamien, zoulou, navajo). En Europe, seuls le limbourgeois (idiome transitionnel entre le bas et le moyen-allemand), le lituanien et le suédois sont des langues tonales.
Le Ton comme Note est la Tonique de la Tonalité d'un morceau musical.
Voir Fonction tonale.
La Musique Tonale est une Musique qui utilise exclusivement les Modes Mineur et Majeur.


En Musique Tonale, la Tonalité est la "couleur sonore" d'un morceau musical, définie par l'association d'un Ton ou Tonique (Degré I de la Gamme diatonique), et d'un Mode (Majeur ou Mineur).
Un morceau musical dans une Tonalité donnée contient donc essentiellement les Notes de la Gamme correspondant à cette Tonalité. Par exemple :
- La Tonalité sol majeur signifie que le morceau musical est basé essentiellement sur les Notes de la Gamme Majeure sol la si do ré mi fa# sol, avec un seul Dièse (fa#) indiqué au niveau de l'Armure de la Clef.
- La Tonalité la majeur signifie que le morceau musical est basé essentiellement sur les Notes de la Gamme Majeure la si do# ré mi fa# sol# la, avec trois Dièses (fa#, do# et sol#) indiqués au niveau de l'Armure de la Clef.
- La Tonalité do mineur signifie que le morceau musical est basé essentiellement sur les Notes de la Gamme Mineure naturelle do ré mib fa sol lab sib do, avec trois Bémols (sib, mib et lab) indiqués au niveau de l'Armure de la Clef.
Le Tableau des Armures ci-dessus (ou le Cycle des quintes équivalent, représenté en Figure ci-dessus) donne toutes les Tonalités possibles en fonction du nombre d'Altérations indiquées au niveau de l'Armure de la Clef.
Tonalités relatives : deux Tonalités ayant même Armure sont dites "relatives". Ainsi, la Tonalité do majeur a pour Tonalité relative la mineur, et réciproquement. A toute Tonalité Majeure correspond une Tonalité Mineure située une Tierce Mineure en-dessous.
Tonalités voisines : pour une Tonalité donnée, on peut identifier cinq Tonalités dites "voisines" relativement au Cycle des Quintes. Ainsi, la Tonalité ré majeur a pour Tonalités voisines : sa Tonalité relative si mineur, la Tonalité Transposée d'une Quinte juste ascendante la majeur et sa relative fa# mineur, la Tonalité Transposée d'une Quinte juste descendante sol majeur et sa relative mi mineur.
Tonalités homonymes : Deux Tonalités de Modes différents (l'un Majeur, l'autre Mineur) et ayant la même Tonique sont dites "homonymes". Ainsi, la Tonalité do majeur a pour Tonalité homonyme do mineur, et réciproquement.
En pratique, pour déterminer la Tonalité d'un morceau musical, la méthode est la suivante :
Etape 1 : Identification de la Tonique en Tonalité Majeure :
Quatre cas peuvent se présenter (voir Tableau ou Figure ci-dessus) :
- Armure sans aucune Altération : la Tonalité est do majeur (exemple 1 de la Figure relative au Mode Majeur).
- Armure avec Dièses : la Tonalité est le dernier Dièse haussé d'un Demi-ton. Exemple : pour une Armure à 3 Dièses fa, do et sol, la Tonalité est sol# haussé d'un Demi-ton, soit la majeur (exemple 2 de la Figure relative au Mode Majeur).
- Armure avec un seul Bémol : la Tonalité est fa majeur.
- Armure avec plusieurs Bémols : la Tonalité est l'avant-dernier Bémol. Exemple : pour une Armure à 3 Bémols si, mi et la, la Tonalité est mib majeur.
Etape 2 : Identification de la Tonique en Tonalité Mineure :
L'Armure de la Tonalité Mineure est par définition celle du Mode Majeur.
A noter que l'Armure de toute Tonalité Mineure est en fait celle de la Gamme mineure naturelle, les Altérations provenant des autres Gammes Mineures (harmoniques ou mélodiques) étant considérées comme Accidentelles et ne figurant pas à la Clef.
La première Note de la Gamme mineure est alors la première Note de la Gamme majeure, baissée d'une Tierce mineure (autre définition : Degré VI de la Gamme majeure). Voir Tableau ci-dessus.
Exemple : pour une Armure indiquant une Gamme de mib majeur à 3 Bémols si, mi et la, la Tonalité est mib baissé d'une Tierce mineure, soit do mineur (exemples 1, 2 et 3 de la Figure relative au Mode Mineur).
Autre exemple : pour une Armure indiquant une Gamme de do majeur sans aucune Altération, la Tonalité est do baissé d'une Tierce mineure, soit la mineur (exemples 4, 5 et 6 de la Figure relative au Mode Mineur).
Etape 3 : Sélection de la véritable Tonalité du morceau musical :
La véritable Tonalité (Majeure ou Mineure) ne peut être ensuite déterminée que par le contexte du morceau musical.
Cette sélection peut se faire au plus simple en regardant la dernière Note ou le dernier Accord du morceau musical, comme suit :
- Lorsque le morceau est une simple Mélodie, il se termine généralement par l'une des trois Notes de l'Accord parfait de Tonique ;
- Dans le cas contraire, le morceau se termine généralement par un Accord de Tonique et plus rarement de Dominante. La Note cherchée est la Fondamentale de l'Accord.
Voir Degré.
Voir Sonagramme.
La Transposition d'un morceau de musique consiste à décaler toutes ses Notes d'un Intervalle fixe vers l'aigu ou le grave.
Cette technique est utilisée le plus souvent pour que le changement de Ton s'adapte à la Tessiture d'une Voix ou d'un Instrument.


Le Tremolo est un Ornement particulier. On distingue :
- Le Tremolo de répétition (symbole = une ou plusieurs barres épaisses sur la Note, voir Figure 1 ci-dessus), qui est une portion de Trille sur une seule Note.
- Le Tremolo trille (symbole = une ou plusieurs barres épaisses entre Notes, voir Figure 2 ci-dessus), qui est une portion de Trille sur deux Notes ou deux Accords, d'amplitude toujours supérieure à un Ton.
Le Tremolo a pour Durée celle de la Note indiquée ou celle de chacune des deux Notes indiquées.
La répétition des Notes ou l'alternance entre Notes a pour Rythme le nombre de barres indiquées : une barre pour des Croches, deux barres pour des Double croches, etc.
L'indication supplémentaire éventuelle trem signifie répéter ou alterner le plus vite possible selon un Rythme non défini.
Une Triade est un Accord de trois notes.

Le Trille est un Ornement particulier (symbole = "tr" suivi éventuellement d'une ligne ondulée horizontale, voir Figure ci-dessus). C'est une rapide alternance de deux Notes Conjointes, d'amplitude égale à un Ton ou un Demi-ton diatonique, la Note indiquée étant toujours la plus basse.
La Trille a pour Durée la longueur de la ligne ondulée.

Au niveau acoustique, lorsqu'on fait vibrer l'air dans un tuyau, une onde longitudinale traverse le tuyau d'une extrémité à l'autre.
Lorsque la colonne d'air est en oscillation libre (en frappant le tuyau par exemple), elle vibre à la Fréquence Fondamentale f0 selon une vibration non sinusoïdale composée d'une somme de vibrations sinusoïdales correspondant aux Fréquences propres f0, 2 f0, 3 f0... de la colonne d'air (voir Figure ci-dessus représentant les trois premiers Modes de vibration en pression et en vitesse).
Fréquence de chaque vibration sinusoïdale :
Pour un tuyau cylindrique, la Fréquence f de chaque vibration sinusoïdale vaut :
Dans le cas d'un tuyau ouvert aux deux extrémités, avec une ouverture quasi-ouverte au niveau du biseau (exemples : flûte, tuyau à bouche d'orgue) :
f = (1/2) n c/L
Dans le cas d'un tuyau fermé à une seule extrémité, avec une ouverture quasi-fermée au niveau de l'anche (exemples : clarinette, saxophone, hautbois, trompette) ou avec une ouverture totalement fermée à l'autre extrémité (exemple : bourdon d'orgue) :
f = (1/2) (n - 1/2) c/L
n est le rang de la Fréquence Harmonique (n = 1 pour la Fondamentale f0),
c est la vitesse de propagation de l'onde sonore le long du tuyau (en m/s),
ρ est la masse volumique de la colonne d'air au repos (en kg/m3),
L est la longueur du tuyau (en m).
Ainsi, un tuyau fermé donne la même Note qu'un tuyau ouvert de longueur double (f0 = (1/4) c/Ltuyau fermé).
Equation de la vibration de la colonne d'air en oscillation libre :
La surpression p(x, t) de la colonne d'air par rapport à la pression atmosphérique est liée à sa vitesse v(x, t) par la relation générale suivante (cf [ISRA, p.54]) :
dp(x, t)/dt = (-ρ c2) dv(x, t)/dx
Dans le cas d'un tuyau cylindrique ouvert aux deux extrémités (x = 0 et x = L), les fonctions p(x, t) et v(x, t) s'écrivent en fonction de l'espace (x) et du temps (t) comme suit (cf [ISRA, p.57]) :
p(x, t) = ∑k=1, +infin;[ ( Ak cos(2 π k f0 t) + Bk sin(2 π k f0 t) ) sin(π k x/L) ]
v(x, t) = (1/(ρ c)) ∑k=1, +infin;[ ( Bk cos(2 π k f0 t) - Ak sin(2 π k f0 t) ) cos(π k x/L) ]
pour lesquels les conditions limites suivantes sont respectées : p(x = 0, t) = 0 et p(x = L, t) = 0
Dans le cas d'un tuyau cylindrique fermé uniquement à l'embouchure (x = 0), les fonctions p(x, t) et v(x, t) s'écrivent en fonction de l'espace (x) et du temps (t) comme suit (cf [COURT, p.1B40]) :
p(x, t) = ∑k=1, +infin;[ ( Ak cos(2 π (n - 1/2) f0 t) + Bk sin(2 π (n - 1/2) f0 t) ) cos(π (n - 1/2) x/L) ]
v(x, t) = (1/(ρ c)) ∑k=1, +infin;[ ( -Bk cos(2 π (n - 1/2) f0 t) + Ak sin(2 π (n - 1/2) f0 t) ) sin(π (n - 1/2) x/L) ]
pour lesquels les conditions limites suivantes sont respectées : v(x = 0, t) = 0 et p(x = L, t) = 0
Dans le cas d'un tuyau cylindrique fermé uniquement à l'autre extrémité (x = L), les fonctions p(x, t) et v(x, t) s'écrivent en fonction de l'espace (x) et du temps (t) comme suit :
p(x, t) = ∑k=1, +infin;[ ( Ak cos(2 π (n - 1/2) f0 t) + Bk sin(2 π (n - 1/2) f0 t) ) cos(π (n - 1/2) (1 - x/L)) ]
v(x, t) = (1/(ρ c)) ∑k=1, +infin;[ ( Bk cos(2 π (n - 1/2) f0 t) - Ak sin(2 π (n - 1/2) f0 t) ) sin(π (n - 1/2) (1 - x/L)) ]
pour lesquels les conditions limites suivantes sont respectées : p(x = 0, t) = 0 et v(x = L, t) = 0
Dans tous ces cas, l'onde longitudinale de la colonne d'air est une combinaison linéaire d'ondes Stationnaires, mais sans que l'onde soit elle-même Stationnaire (cf [THIB, p.27]).
Les coefficients Ak et Bk dépendent des conditions initiales de la colonne d'air (à t = 0).
Equation de la vibration de la colonne d'air en oscillation forcée :
On force l'embouchure du tuyau située en x = 0 à osciller à une Fréquence F fixée de l'extérieur (par une source sonore continue, par exemple : haut-parleur, biseau de flûte ou de bourdon d'orgue, anche de clarinette ou de trompette)
L'onde produite, qui est une surpression p(x = 0, t) ou une vitesse v(x = 0, t) selon que le flux d'air de la source est commandé en pression ou en vitesse, se réfléchit à l'autre extrémité du tuyau (x = L), en grande partie lorsque l'extrémité est ouverte ("mur d'air") ou complètement lorsque l'extrémité est fermée (bouchon). En revenant dans l'autre sens, l'onde réfléchie interfère avec l'onde incidente avec la même Fréquence, Longueur d'onde et amplitude, mais sans que la phase soit nécessairement identique. En phase ou non, la superposition de ces deux ondes, incidente et réfléchie, crée une nouvelle onde qui, elle, est fixe et appelée onde Stationnaire (cf [BOU Résonance]).
En outre, la source étant en régime forcé, le mouvement de va-et-vient des ondes dans le tuyau renforce à chaque passage la situation établie. Si toutes les conditions sont réunies pour que l'interférence soit constructive, un phénomène nouveau intervient alors, la Résonance, qui a pour conséquence la multiplication de l'amplitude de l'onde Stationnaire qui augmente jusqu'à la limite permise par le tuyau selon ses possibilités d'amortissement (cf [BOU Résonance]).
Dans le cas d'un tuyau cylindrique ouvert aux deux extrémités (x = 0 et x = L), les équations en fonction de l'espace (x) et du temps (t) sont alors les suivantes :
Dans le cas d'un flux d'air commandé en pression (haut-parleur devant un tube ouvert à l'autre extrémité), les équations de la colonne d'air s'écrivent comme suit (cf [GAB Acoustique]) :
p(x, t) = A cos(2 π F t) sin(2 π F (L - x)/c) / sin(2 π F L/c)
v(x, t) = (1/(ρ c)) A sin(2 π F t) cos(2 π F (L - x)/c) / sin(2 π F L/c)
pour laquelle les conditions limites suivantes sont respectées : p(x = 0, t) = A cos(2 π F t) et p(x = L, t) = 0
Dans le cas d'un flux d'air commandé en vitesse (biseau d'instrument, cf [BENADE Les bois]), les équations de la colonne d'air s'écrivent comme suit (cf [GAB Acoustique]) :
v(x, t) = A cos(2 π F t) cos(2 π F (L - x)/c) / cos(2 π F L/c)
p(x, t) = -(ρ c) A sin(2 π F t) sin(2 π F (L - x)/c) / cos(2 π F L/c)
pour laquelle les conditions limites suivantes sont respectées : v(x = 0, t) = A cos(2 π F t) et p(x = L, t) = 0
Dans le cas d'un tuyau cylindrique fermé uniquement à l'embouchure (x = 0), le flux d'air est généralement commandé en pression (anche d'instrument ou anche lippale, cf [BENADE Les bois]) et les équations de la colonne d'air s'écrivent alors comme suit :
Attention : équations à confirmer, démonstration non trouvée.
p(x, t) = A cos(2 π F t) sin(2 π F (L - x)/c) / sin(2 π F L/c)
v(x, t) = (1/(ρ c)) A sin(2 π F t) cos(2 π F (L - x)/c) / sin(2 π F L/c)
pour laquelle les conditions limites suivantes sont respectées : p(x = 0, t) = A cos(2 π F t) et p(x = L, t) = 0
Dans le cas d'un tuyau cylindrique fermé uniquement à l'autre extrémité (x = L), les équations de la colonne d'air s'écrivent alors comme suit :
Dans le cas d'un flux d'air commandé en pression (haut-parleur devant un tube fermé à l'autre extrémité), les équations de la colonne d'air s'écrivent comme suit :
Attention : équations à confirmer, démonstration non trouvée.
p(x, t) = A cos(2 π F t) cos(2 π F (L - x)/c) / cos(2 π F L/c)
v(x, t) = -(1/(ρ c)) A sin(2 π F t) sin(2 π F (L - x)/c) / cos(2 π F L/c)
pour laquelle les conditions limites suivantes sont respectées : p(x = 0, t) = A cos(2 π F t) et v(x = L, t) = 0
Dans le cas d'un flux d'air commandé en vitesse (biseau de bourdon d'orgue, cf [BENADE Les bois]), les équations de la colonne d'air s'écrivent comme suit (cf [COURT, p.1B40]) :
v(x, t) = A cos(2 π F t) sin(2 π F (L - x)/c) / sin(2 π F L/c)
p(x, t) = (ρ c) A sin(2 π F t) cos(2 π F (L - x)/c) / sin(2 π F L/c)
pour laquelle les conditions limites suivantes sont respectées : v(x = 0, t) = A cos(2 π F t) et v(x = L, t) = 0
Dans tous ces cas, les termes spatial (x) et temporel (t) étant découplés, la surpression p(x, t) ou la vitesse v(x, t) de la colonne d'air est l'équation d'une onde Stationnaire.
Par ailleurs, lorsque la Fréquence de forçage F correspond approximativement à une Fréquence propre de la colonne d'air (n f0 avec n pair ou impair selon les cas), celle-ci se met en Résonance (cf [BOU Résonance]). L'amplitude de l'onde stationnaire tend alors vers l'infini jusque la limite permise par le tuyau selon ses possibilités d'amortissement.
Pour certains Instruments à vents (le haut-bois par exemple), l'oscillation forcée est entretenue par un mécanisme à rétroaction qui transforme l'application continue d'une pression en une perturbation acoustique oscillante audible (cf [BENA, Les cuivres]).
Un Unisson (ou Prime) est l'Intervalle qui sépare deux Notes de même Degré dans la Gamme diatonique.
L'Unisson juste correspond à 0 Ton et 0 Demi-ton. Il a pour rapport 1/1 (soit une largeur de 0 Octave). Exemple en do Majeur : do - do.
Voir Répétition.
Voir Nuance.
Un vibrateur est un appareil qui produit des vibrations (Corde vibrante, colonne d'air vibrante contenue dans un Tuyau sonore, Membrane vibrante, Plaque vibrante, autres procédés de percussion, électronique).
Le vibrateur est généralement couplé à une Caisse de résonance chargée de recevoir et d'amplifier par Résonance le son produit par le vibrateur.

Le Vibrato est un Ornement particulier (symbole = ligne ondulée horizontale, voir Figure ci-dessus). C'est une petite fluctuation continue de Hauteur sur une ou plusieurs Notes, d'amplitude inférieure à un Demi-ton.
Le Vibrato a pour Durée la longueur de la ligne ondulée, pour amplitude son épaisseur et pour vitesse le rapprochement entre ses ondulations.
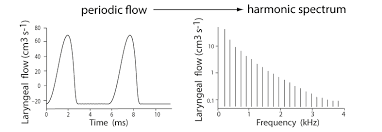
Le Voisement est l'action de faire vibrer les cordes vocales, le son produit s'appelant la Voix (cf [MARTINET, Eléments, p.39]).
La vibration est assimilable approximativement à un signal triangulaire harmonique de Fréquence Fondamentale F0 (cf [CAIL]). Voir Figure ci-dessus.
La vibration ou l'absence de vibration des cordes vocales permet de distinguer entre Phonèmes voisés et Phonèmes non-voisés.
Dans le cas voisé, on emploie le terme "voisé" ou "sonore". En prononciation française, toutes les Voyelles, Semi-voyelles, Consonnes nasales et Consonnes liquides sont voisées, ainsi que certaines autres Consonnes dites "sonores" ("b", "d", "g", "v", "z", "j").
Dans le cas contraire (absence de vibration), on emploie le terme "non-voisé" ou "sourd", ce qui est aussi le cas de la parole chuchotée.
Définition :
En musique, la Voix (ou Partie) est la Ligne mélodique confiée à chaque exécutant dans une composition vocale et/ou Instrumentale.
Sur une partition d'orchestre, les différentes Voix sont notées par Familles d'Instruments, allant de l'Instrument le plus aigu au plus grave pour chaque Famille.
La voix humaine et son Appareil vocal :
La voix humaine comprend le chant, la parole, le cri et le rire.
A noter qu'on peut chanter en voix parlée (rap, comédie musicale, etc.) et parler en voix chantée (déclamation).
Dans le chant et le Langage parlé, la Hauteur de la Ligne mélodique est la Fréquence Fondamentale F0 produite par les cordes vocales. Les Harmoniques sont concentrés dans des zones Formantiques qui caractérisent les Voyelles et les Consonnes sonantes (voir Sonagramme).
En musique instrumentale, la Hauteur de la Note est également la Fréquence Fondamentale F0 produite par le Vibrateur (Corde vibrante, colonne d'air vibrante, Membrane vibrante, etc.). Les Harmoniques ont par contre un Spectre sonore caractéristique du type d'Intrument de musique (voir Sonagramme).
Les voix chantées :
Les Voix chantées sont classées comme Instruments à vent.
Dans la Famille des voix chantées, il existe une typologie des voix, avec, pour chacune, une étendue de Notes appelée Tessiture :
- les Sopranos, ou voix aigües de femmes et d'enfants,
- les Mezzo-sopranos, ou voix moyennes de femmes et d'enfants, voire d'hommes,
- les Altos ou Contraltos, ou voix graves de femmes et d'enfants, voire d'hommes,
- les Ténors, ou voix aigües d'hommes,
- les Barytons, ou voix moyennes d'hommes ;
- les Basses, ou voix graves d'hommes.
Les Parties extrêmes sont les Sopranos et les Basses. Toutes les autres Voix sont dites "Parties intermédiaires".
Les Parties que l'on perçoit le plus sont d'abord la Voix supérieure, ensuite la Basse, enfin seulement les Parties intermédiaires.
Lorsqu'une Voix passe au-dessus d'une Voix immédiatement supérieure, on dit qu'il y a Croisement.
L'Ecartement entre Voix fait l'objet de règles harmonieuses.
Voix chantée et voix parlée :
Par rapport au Langage parlé, le chant est moins intelligible pour plusieurs raisons (cf [SCOTTO]) :
- Phonèmes sous-articulés dû à un Conduit vocal totalement dégagé pour les besoins de la voix chantée,
- Phonèmes distordus par l'Intensité (par exemple, entre 90 et 130 dB, ne restent que trois types de Timbres pour les Voyelles /i/ /a/ et /u/),
- Phonèmes distordus par la Fréquence Fondamentale (par exemple, entre 440 Hz (la3) et 659 Hz (mi4), seules les Voyelles /i/ et /a/ sont différenciées ; au-dessus de 659 Hz, les Voyelles ne se distinguent plus les unes des autres),
- Phonèmes masqués par le Vibrato et le Singing Formant,
- Mots distordus par l'allongement considérable des Syllabes et la baisse du Débit d'élocution,
- Mots mal prononcés dans les cas d'une mauvaise association entre Notes et Syllabes dans le livret de chant,
- Mots mal compris dans les cas de décalage entre accent syllabique (Accent tonique) et accent musical (Temps fort) dans le livret de chant,
- Voix des chanteurs masquée par celle des musiciens.
Voir Phonème.
Les auteurs cités dans cette page sont mentionnés entre crochets sous la forme [AUTEUR Titre Page].
 Dernière mise à jour de la page : 13 novembre 2025.
Dernière mise à jour de la page : 13 novembre 2025.