Site de Régis Petit

Relativité

Préambule ( Paragraphe Début / Suivant )

Cette page donne les formules fondamentales de la Relativité Restreinte et de la Relativité Générale avec une présentation des outils mathématiques accessible aux non-initiés.
Cette page comporte également un Lexique détaillé des termes utilisés en Relativité.
Notations de cette page :
- Les mots-clés ont leur première lettre indiquée en majuscule et sont définis dans le Lexique.
- Les auteurs cités sont mentionnés entre crochets sous la forme [AUTEUR Titre Page]. Voir Bibliographie.
- Les Notations mathématiques sont conformes, sauf rares exceptions, à celles de Eric Gourgoulhon, Directeur de recherche au CNRS [GOU, Relativité Restreinte][GOU, Relativité Générale].
- Les Conventions de signe sont classiquement celles de Misner, Thorne et Wheeler (MTW), avec un Tenseur métrique de Signature (-, +, +, +), un Tenseur de courbure défini par Rⁱjkl = Γⁱjl_,k + ..., et un Tenseur de Ricci défini par Rij = R^kikj

Sommaire de cette page ( Paragraphe Précédent / Suivant )

1. Qu'est-ce que la Relativité ?
   1. Les trois étapes de la relativité
   2. Relativité du temps
   3. Les "mystères" de l'espace-temps
   4. Au-delà d'Einstein : la causalité universelle
2. Relativité Restreinte
   1. Historique
   2. Transformation de Lorentz-Poincaré
   3. Démonstration
3. Relativité Générale
   1. Historique
   2. L'équation d'Einstein
   3. Résolution de l'équation d'Einstein
   4. Résolution de l'équation d'Einstein avec la Métrique de Schwarzschild
   5. Résolution de l'équation d'Einstein avec la Métrique de Friedmann-Lemaître-Robertson-Walker
   6. Décalages spectraux
4. Lexique
5. Bibliographie

1. Qu'est-ce que la Relativité ? ( Paragraphe Précédent / Suivant )

1.1. Les trois étapes de la relativité ( Sous-paragraphe Début / Suivant )

L'idée de relativité ne date pas d'Einstein mais trouve son origine dans les travaux de Galilée.

On considère deux Observateurs en mouvement relatif dont les référentiels sont en translation rectiligne et à vitesse uniforme l'un par rapport à l'autre. Ces référentiels sont dits inertiels.

• En relativité galiléenne, il y a invariance des lois de la Mécanique classique par changement de référentiel inertiel.
  Le temps est absolu et les Observateurs obtiendront chacun dans son référentiel les mêmes résultats en faisant les mêmes expériences de Mécanique classique.
  
  
• En Relativité Restreinte ("RR" en abrégé), l'invariance en relativité galiléenne s'étend aux lois de l'Electromagnétisme.
  Le temps n'est plus absolu et devient inséparable de l'espace (notion d'Espace-temps). La Transformation de Galilée devient la Transformation de Lorentz-Poincaré. Les lois de la Mécanique classique deviennent les lois de la Mécanique relativiste (mais en excluant la gravitation Newtonienne).
  A noter que la Relativité Restreinte n'interdit pas d'étudier le point de vue d'Observateurs accélérés en utilisant des référentiels instantanément Comobiles, c'est-à-dire des référentiels inertiels instantanés qui coïncident momentanément avec l'observateur accéléré à chaque instant de son trajet.
  Ainsi, le cadre cinématique proposé par la Relativité Restreinte est tout à fait universel. La Relativité Générale n'est requise que si l'on doit tenir compte d'effets gravitationnels [SPA, L'expérience].
  A noter que le livre d'Eric Gourgoulhon [GOU, Relativité Restreinte] est l'un des seuls à traiter d'abord des mesures effectuées dans l'Espace-temps par un Observateur quelconque (pouvant être accéléré ou en rotation) et à traiter ensuite du cas particulier des Observateurs inertiels.
  En résumé, la Relativité Restreinte s'applique à un Espace-temps où les effets gravitationnels sont complètement négligés, et selon des équations simples lorsque les référentiels sont en translation rectiligne uniforme.
  
  
• En Relativité Générale ("RG" en abrégé), l'invariance en Relativité Restreinte s'étend à la gravitation et à tout type de changement de référentiel (uniforme ou accéléré).
  La gravitation Newtonienne devient la gravitation relativiste (Equation d'Einstein) et les lois de la Physique sont mises sous forme tensorielle afin d'être indépendantes du système de coordonnées.
  

Aujourd'hui, il reste un dernier défi à relever : l'unification de la Relativité Générale et de la Théorie quantique afin de rendre cohérent la gravitation à l'échelle macroscopique et la gravitation à l'échelle microscopique faisant intervenir le caractère quantique des particules élémentaires.

1.2. Relativité du temps ( Sous-paragraphe Précédent / Suivant )

La relativité du temps, que ce soit en relativité Restreinte ou Générale, englobe deux phénomènes distincts souvent confondus :
- la relativité de la simultanéité
- la multiplicité des temps propres

1.2.1. Relativité de la simultanéité :

Des événements simultanés pour un observateur peuvent ne pas l'être pour un autre en mouvement relatif par rapport au premier.
Ce phénomène réel n'est pas mystérieux en soi car il résulte logiquement de la vitesse de la lumière qui est finie, combinée à l'invariance de la vitesse de la lumière dans tous les référentiels inertiels par rapport au mouvement de la source lumineuse et de l'observateur.

"A l'échelle humaine, la vitesse de la lumière est prodigieusement grande (environ 300 000 km/s). Lorsqu'une source lumineuse quelconque nous envoie un signal, la lumière nous apporte une information quasi-instantanée. Nous croyons voir l'espace à un instant donné. Le temps nous semble absolu, séparé de l'espace." [AND Théorie - Partie 1]
Imaginons deux Observateurs O et O', en mouvement relatif l'un par rapport à l'autre, qui veulent régler leurs montres par échange de signaux optiques. Supposons que les deux montres soient synchronisées, par un moyen quelconque, de façon qu'elles indiquent la même heure à un même instant initial. A cet instant, chaque Observateur émet un signal vers l'autre. Quel temps indique alors chaque montre quand chaque Observateur reçoit le signal de l'autre ? Il est évident que ce n'est pas le même temps.
Et Poincaré explique : "La durée de la transmission n'est pas la même dans les deux sens puisque l'Observateur O, par exemple, marche au devant de la propagation optique émanée de O', tandis que l'Observateur O' fuit devant la propagation émanée de O. Les montres marqueront ce qu'on peut appeler le temps local de chaque Observateur, de sorte que l'une d'elles retardera sur l'autre. Peu importe puisque nous avons aucun moyen de nous en apercevoir..." [POI L'Etat, p.311]
Le temps indiqué est le même pour les deux Observateurs uniquement dans le cas d'Observateurs fixes l'un par rapport à l'autre ou dans l'hypothèse de pensée d'une lumière ayant une vitesse infinie. Dans les autres cas, on parle de dilatation apparente des durées.
Ainsi, "l'univers instantané n'est pas observable. Il apparaît comme un Espace-temps où chaque objet observé est vu en un point de l'espace et en un point du temps qui n'est pas le même pour tous les points de l'espace." [AND Théorie - Partie 1]


1.2.2. Multiplicité des temps propres :

Le temps propre mesuré par un observateur immobile dans son référentiel est unique à cet observateur. Deux observateurs en mouvement relatif l'un par rapport à l'autre, ou soumis à des champs gravitationnels différents, accumuleront des temps propres différents même s'ils se retrouvent au même point de l'espace-temps.
Ce phénomène réel reste à ce jour mystérieux et résulte des propriétés de l'espace-temps concernant à la fois :
1. le mouvement relatif des observateurs (principe de relativité restreinte).
2. la présence de champs gravitationnels (déformation physique de l'espace-temps).

1.3. Les "mystères" de l'espace-temps ( Sous-paragraphe Précédent / Suivant )

La théorie de la Relativité, bien que mathématiquement cohérente et expérimentalement vérifiée, ne fournit pas toujours des explications intuitives des phénomènes qu'elle décrit. La Multiplicité des temps propres en fait partie, illustrant les limites de notre compréhension intuitive de l'univers à grande échelle. [PER]
A cela s'ajoutent certaines maladresses ne facilitant pas la lecture et la compréhension de la Relativité. On peut citer :

• 1. Points de vue différents :
  Par exemple, le concept de Temps est utilisé différemment (sans être contradictoire) par les auteurs. Pour les matheux, le temps se réduit à une variable purement opératoire. Pour les physiciens, le temps représente au contraire un temps physique qui est le temps réel mesuré au moyen d'horloges localisées spatialement et susceptibles de se synchroniser en échangeant des signaux lumineux.
  
  
• 2. Manque de rigueur dans l'utilisation des mots :
  Par exemple, Temps et Durée sont parfois confondus, la durée étant l'intervalle de temps séparant deux événements.
  De même pour Temps propre et Temps apparent qui sont deux temps distincts mesurés dans des conditions différentes.
  De même pour temps physique et temps biologique qui sont aussi deux temps distincts.
  Autre exemple : Position et Image d'un objet en mouvement sont souvent confondues.
  
  
• 3. Conventions de signe non explicitées :
  Certains auteurs utilisent implicitement d'autres conventions de signe que les Conventions de signe classiques (MTW), ce qui change le signe de certains Tenseurs (dont celui du Tenseur métrique (g)) et/ou celui de la Constante cosmologique (Λ) et/ou celui du Coefficient de couplage gravitationnel (K).
  
  
• 4. Simplification excessive d'écriture :
  Certains auteurs allègent l'écriture des formules en éliminant certaines constantes. La vérification de l'homogénéité des formules n'est plus possible et peut faire place à des erreurs dans l'application numérique de ces formules.
  La vitesse de la lumière (c), la constante de gravitation universelle (G) et/ou la permittivité diélectrique dans le vide (ε₀) sont parfois mises arbitrairement à 1.
  Exemple 1 : le coefficient de couplage gravitationnel est parfois écrit : K = 8 π au lieu de : K = 8 π G c^-4
  Exemple 2 : la relation d'Einstein est parfois écrite : E² = m² + P.P    au lieu de : E² = m² c⁴ + P.P c²
  Exemple 3 : la première équation de Friedmann est parfois écrite : (da/dt)² = (1/3) (8 π G ρ + Λ) a² - k    au lieu de : (da/(cdt))² = (1/3) (8 π G ρ/c² + Λ) a² - k
  
  
• 5. Généralisation abusive :
  Beaucoup d'auteurs ne mentionnent qu'une partie des conditions d'applicabilité des formules. Les résultats publiés héritent alors à tort d'un statut général.
  Par exemple, en Relativité Générale, beaucoup de formules concernent implicitement un espace vide (de tout champ non gravitationnel) avec Constante cosmologique nulle.
  
  
• 6. Présentation insuffisamment pédagogique :
  Peu d'auteurs produisent un index des notations utilisées.
  Peu d'auteurs respectent rigoureusement la notation vectorielle qui distingue les grandeurs scalaires (lettres non grasses), vectorielles (lettres grasses) et tensorielles (lettres grasses majuscules).
  Peu d'auteurs placent la démonstration des formules (souvent longue) après leur énoncé, idéalement dans un encart déporté.
  Peu d'auteurs produisent, en complément du texte, des exemples et des schémas illustratifs (interprétations géométriques par exemple).
  
  
• 7. Emprunt de texte sans référence de la source :
  Peu d'auteurs indiquent la référence des extraits de texte empruntés (auteur, titre, page).
  
  
• 8. Accès non libre aux documents Internet :
  Peu d'auteurs (enseignants ou chercheurs) donnent librement accès à leur cours sur Internet.
  

1.4. Au-delà d'Einstein : la causalité universelle ( Sous-paragraphe Précédent / Début )

Le postulat d'Einstein stipule que la vitesse de la lumière dans le vide est invariante dans tous les référentiels inertiels par rapport au mouvement de la source lumineuse et de l'observateur.
Ce postulat d'invariance n'est pas strictement nécessaire d'un point de vue mathématique et peut être remplacé par le postulat de causalité qui est plus général et moins artificiel [SEM]. Ce dernier montre en effet qu'il existe une vitesse limite de propagation des interactions (Constante de structure de l'espace-temps) sans nécessairement spécifier que cette vitesse soit celle de la lumière.
Cependant, bien que mathématiquement équivalents, ces deux postulats offrent des perspectives différentes sur l'interprétation physique de la théorie de la Relativité.
Le postulat d'Einstein est plus spécifique, identifiant explicitement la vitesse de la lumière comme la vitesse limite. Ce postulat, combiné au principe de Relativité Restreinte, donne le principe d'invariance de la vitesse de la lumière.
En conséquence :
- La vitesse de la lumière n'est qu'une manifestation spécifique de cette limite dans le cadre de l'électromagnétisme.
- La remise en cause hypothétique de la vitesse de la lumière dans le vide comme limite absolue n'est pas nécessairement une remise en cause de la théorie de la Relativité Restreinte.
- Le postulat de causalité pourrait s'appliquer même dans des situations où la lumière ne jouerait pas un rôle central, par exemple dans certaines théories de gravité quantique.

2. Relativité Restreinte ( Paragraphe Précédent / Suivant )

2.1. Historique ( Sous-paragraphe Début / Suivant )

- Jusqu'à la fin du 19^e siècle, la mécanique classique, fondée par Galilée et Newton, constituait une base incontestée de la physique.
- En 1887, un physicien américain, Albert Michelson, et son collègue Edward Morley, montrèrent que la vitesse de la lumière ne vérifiait pas la loi galiléenne d'addition des vitesses. La vitesse de la lumière dans le vide était au contraire indépendante du mouvement de la source émettrice.
- A la fin du 19^e siècle, une seconde énigme vient perturber les certitudes des savants. Les fameuses Equations du britannique James Clerk Maxwell, qui décrivent la totalité des phénomèmes de l'électromagnétisme, n'ont plus la même forme lorsqu'on les transpose d'un système de référence dans un autre par translation rectiligne uniforme.
Le principe galiléen ne devrait-il pas être, sinon abandonné, tout au moins réadapté ?
- En 1905, Jules Henri Poincaré pose les bases fondamentales de la Relativité Restreinte qui efface d'un seul coup toutes les angoisses des physiciens concernant ces deux énigmes [POI L'Etat].
Il montre que la véritable base de la Relativité Restreinte est la transformation de Lorentz-Poincaré qui généralise celle de Galilée aux vitesses non négligeables par rapport à celle de la lumière.
- En 1905 également, Albert Einstein publie sa théorie de la Relativité Restreinte [EIN Zur_Elektrodynamik].
Elle est basée également sur la transformation de Lorentz-Poincaré mais selon une interprétation physique différente de celle de Poincaré : la Relativité Restreinte a pour fondement la vitesse relative de deux objets et non pas leur vitesse par rapport à un référentiel absolu (l'éther).
- Cette transformation ouvre la voie à des concepts révolutionnaires qui ont été ensuite vérifiés expérimentalement. On peut citer :
   1932 : L'invariance de la vitesse de la lumière (suggérée en 1887 par Michelson & Morley en montrant que l'éther luminifère n'existe pas, puis postulée en 1905 par Albert Einstein, puis démontrée en 1932 par Roy Kennedy et Edward Thorndike en vérifiant que la vitesse de la lumière est indépendante du mouvement de la source).
   1930-1950 : La composition relativiste des vitesses (validée indirectement par de nombreux laboratoires dans les accélérateurs de particules).
   1938 : La dilatation des durées (démontrée par Herbert Ives et G.R. Stilwell en mesurant le décalage Doppler de la lumière émise par des ions en mouvement rapide).
   1941 : La contraction des longueurs (démontrée indirectement par Bruno Rossi et David B. Hall via l'expérience des muons cosmiques).
   1971 : La multiplicité des temps propres (confirmée par Hafele & Keating avec des horloges atomiques embarquées dans des avions faisant le tour du monde).
   2008 : L'équivalence masse-énergie (confirmée indirectement dans les années 1930-1940 par de nombreuses expériences en physique nucléaire et des particules, puis confirmée en 2008 par l'équipe internationale du Centre de Physique Théorique de Marseille en montrant que la masse du proton provient de l'énergie des quarks et des gluons).
   2011 : L'aberration relativiste de la lumière (démontrée directement par l'équipe de Daniel Giovannini de l'Université de Glasgows, en laboratoire terrestre).

A noter quelques conclusions surprenantes parmi d'autres :
- Si deux particules lumineuses s'éloignent l'une de l'autre, leur vitesse relative est encore égale à c et non pas 2c (loi de composition des vitesses. Voir ci-dessous).
- La vitesse de la lumière étant ralentie dans des milieux divers selon leur indice n de réfraction, il est possible d'accélérer des particules qui vont plus vite que la lumière dans ce même milieu.

2.2. Transformation de Lorentz-Poincaré ( Sous-paragraphe Précédent / Suivant )

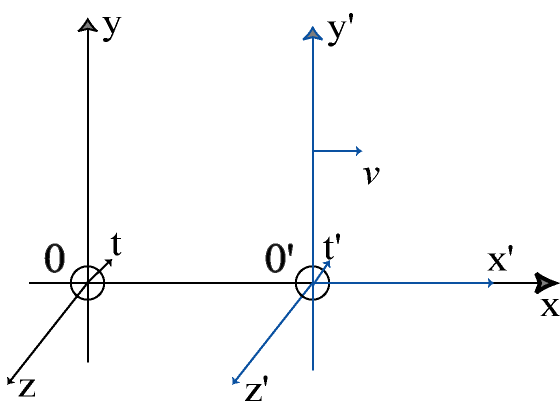
Hendrik Antoon Lorentz a donné une version imparfaite de cette transformation en 1899 puis 1904. Jules Henri Poincaré a publié les équations correctes en 1905, en les baptisant du nom de Lorentz.


Hypothèses :
Initialement, deux référentiels orthonormés R et R' ont leurs origines O et O' confondues à t = t' = 0, avec leurs axes x et x', y et y', z et z' respectivement parallèles.
Ensuite, le référentiel R' effectue une translation rectiligne uniforme par rapport à R à une vitesse constante v, mesurée dans R et dans le sens positif de l'axe x.
Soit un point ou événement quelconque M de coordonnées spatio-temporelles (x, y, z, t) dans R et (x', y', z', t') dans R'.

La transformation de Galilée faisant passer de R à R' s'écrit classiquement :

La transformation de Lorentz-Poincaré introduit une nouvelle entité pour décrire les phénomènes physiques : l'Espace-temps. Cette conception unifie l'espace et le temps en une seule structure à quatre dimensions, expliquant notamment les deux phénomènes suivants :
1. Contraction apparente des longueurs : La longueur d'un objet en mouvement par rapport à un observateur apparaît contractée dans la direction du mouvement lorsque mesurée par cet observateur. Les dimensions de l'objet perpendiculaires au mouvement ne sont pas affectées. Ce phénomène est symétrique : chaque observateur voit les objets de l'autre référentiel contractés dans la direction du mouvement.
2. Dilatation apparente des durées : L'intervalle de temps entre deux événements se produisant au même endroit dans un référentiel donné apparaît plus long lorsqu'il est mesuré depuis un référentiel en mouvement par rapport au premier. Ce phénomène est symétrique : chaque observateur voit les durées dans l'autre référentiel s'allonger.
Les équations correspondantes s'écrivent :

c est une constante (Constante de structure de l'espace-temps) qui s'apparente à une vitesse limite et qui apparaît au cours de la démonstration des équations (L). La constante c est prise égale à la plus grande vitesse mesurée actuellement qui est celle des phénomènes électromagnétiques dans le vide, en l'occurence la vitesse de la lumière dans le vide.

La transformation inverse consiste à remplacer v par -v dans les relations (L1) à (L4) :

Lorsque la vitesse v a une direction quelconque par rapport à l'axe x, la transformation de Lorentz-Poincaré s'écrit sous forme vectorielle comme suit (en notant r = (x, y, z) et r' = (x', y', z')) :

Lorsque v est parallèle à l'axe des x et de même sens, on a v = (v, 0, 0) et r = (x, y, z), d'où : v.r = v x
La relation (LL1) projetée sur l'axe des x devient : x' = x + (γ - 1) x - γ v t = γ (x - v t)
La relation (LL1) projetée sur l'axe des y devient : y' = y
La relation (LL1) projetée sur l'axe des z devient : z' = z
La relation (LL2) devient : t' = γ(t - v x / c²)
On retrouve les relations standard (L1) à (L4).

Lorsque v et r sont parallèles, on a r = r (v/v) et les relations (LL1)(LL2) deviennent : r' = γ (r - v t) (v/v)   et t' = γ (t - v r / c²)
Ainsi, la position r reste inchangée en direction mais est modifiée en magnitude en fonction de la vitesse v et du temps t. De même, le temps t est modifié en fonction de la vitesse v et de la position r.

Lorsque v et r sont perpendiculaires, on a v.r = 0 et les relations (LL1)(LL2) deviennent : r' = r - γ v t   et t' = γ t
Ainsi, la position r reste inchangée mais subit un déplacement supplémentaire ( - γ v t ) dans la direction du mouvement. Le temps t est simplement augmenté d'un facteur γ, sans aucune dépendance à la position.

Les deux cas précédents mettent en évidence les points suivants :
- L'entrelacement espace-temps plus prononcé dans le cas parallèle.
- La simplicité relative de la transformation dans le cas perpendiculaire.

2.3. Démonstration ( Sous-paragraphe Précédent / Début )

- En 1975, Jean-Marc Lévy-Leblond publie un article sur la Relativité Restreinte présenté sous forme moderne déduite uniquement des propriétés de l'espace et du temps, sans recours à l'électromagnétisme [LEV].
- En 2001, Jean Hladik publie, avec l'un de ses collègues Michel Chrysos, le premier ouvrage en français sur la Relativité Restreinte présenté sous cette forme moderne, en titrant ces propriétes de "postulats de Poincaré" [HLA Pour_comprendre].
Les principales conclusions sont alors les suivantes :
- Les quatre postulats de Poincaré suffisent à mettre en avant la transformation de Lorentz-Poincaré et sa limite dégénérée galiléenne comme les seules transformations inertielles possibles [LEV].

En s'inspirant des ouvrages [LEV][HLA, Pour_comprendre][HLA, Initiation][CAS][SEM], nous présentons ci-dessous une démonstration complète de la transformation de Lorentz-Poincaré, basée uniquement sur les quatre postulats de Poincaré.

3. Relativité Générale ( Paragraphe Précédent / Suivant )

3.1. Historique ( Sous-paragraphe Début / Suivant )

- En 1907, Albert Einstein énonce le Principe d'équivalence selon lequel les effets de la gravitation sont localement indiscernables d'une accélération.
- Entre 1907 et 1915, Einstein postule que toutes les lois de la Nature doivent avoir la même forme dans tous les référentiels, quel que soit leur état de mouvement (uniforme ou accéléré).
Pour exprimer cette covariance des lois physiques, il développe les outils mathématiques nécessaires avec l'aide de divers mathématiciens, dont David Hilbert [PETIT, Physique, p.28], intégrant ainsi la géométrie non-euclidienne et le calcul tensoriel.
- En 1915, Einstein publie l'équation de la gravitation relativiste [EIN Die_Grundlage], repensant complètement la notion de gravitation Newtonienne, laquelle, se propageant instantanément, n'est plus compatible avec l'existence d'une vitesse limite.
- Cette équation ouvre la voie à des concepts révolutionnaires qui ont été ensuite vérifiés expérimentalement. On peut citer :
   1915 : La précession de l'orbite de Mercure (observée dès 1859 par Urbain le Verrier et expliquée en 1915 par Albert Einstein).
   1919 : La déviation de la lumière par le Soleil (prédite en 1915 par Albert Einstein et confirmée en 1919 par Arthur Eddington lors d'une éclipse solaire).
   1929 : L'expansion de l'univers (prédite en 1922 par Alexander Friedmann et observée en 1929 par Edwin Hubble).
   1960 : Le décalage spectral gravitationnel ou effet Einstein (prédit en 1915 par Albert Einstein et observé en 1960 par Pound & Rebka).
   1965 : Le Big Bang (formulé en 1927 par Georges Lemaître et confirmé en 1965 par Arno Penzias et Robert Wilson par la découverte du fonds diffus cosmologique représentant le rayonnement résiduel de l'univers primordial).
   1966 : Le retard de la lumière ou effet Shapiro (prédit en 1964 par Irwin Shapiro et détecté en 1966 et 1967 par l'antenne radar Haystack du MIT).
   1970 : Le système GPS (mis en service dans les années 1970-1980 par le Département de la Défense des Etats-Unis).
   1971 : La dilatation du temps gravitationnel (prédite en 1915 par Albert Einstein et confirmée en 1971 par Hafele & Keating avec des horloges atomiques embarquées dans des avions faisant le tour du monde).
   1979 : L'effet de lentille gravitationnelle (prédit en 1936 par Albert Einstein et observé en 1979 par Dennis Walsh et son équipe sur un quasar double).
   2015 : Les ondes gravitationnelles (prédites en 1916 par Albert Einstein et détectées directement en 2015 par le laser LIGO, collaboration internationale).
   2019 : Les trous noirs (prédits en 1916 par Karl Schwarzschild et observés en 2019 par le télescope EHT, collaboration internationale).

3.2. L'équation d'Einstein ( Sous-paragraphe Précédent / Suivant )

Définition

L'équation fondamentale de la Relativité Générale, connue sous le nom Equation d'Einstein ou Equation de la gravitation relativiste, définit comment la présence de matière et d'énergie déforme localement la géométrie de l'univers (voir Figure ci-dessus).
John Archibald Wheeler, spécialiste américain de la Relativité Générale, résume ainsi la situation : "La matière dit à l'espace-temps de se courber et l'espace-temps dit à la matière comment se déplacer".
Cette équation peut être vue comme une généralisation de la loi d'élasticité de Hooke en milieu continu peu déformé, pour laquelle la déformation d'une structure élastique est proportionnelle à la tension qui s'exerce sur cette structure. Cette équation s'écrit sous forme tensorielle comme suit :

gab est le Tenseur métrique, solution de l'équation d'Einstein, qui définit globalement la géométrie de l'Espace-temps. Les 16 composantes gab de ce Tenseur sont appelées potentiels de gravitation.

Sab est le Tenseur d'Einstein modifié qui mesure la courbure locale de la géométrie de l'Espace-temps. Ce Tenseur a pour propriété remarquable d'avoir une Divergence nulle.
Cette déformation de l'Espace-temps est directement liée à la présence locale de matière et d'énergie via le Tenseur Energie-impulsion Tab qui encode les propriétés de la matière et de l'énergie.
Cependant, cette déformation peut également être causée par des sources distantes, même en l'absence de matière et d'énergie locales (c'est-à-dire lorsque Tab = 0). Dans ce cas, la déformation est décrite par le Tenseur métrique gab qui encode la géométrie de l'Espace-temps.
Ainsi, il n'y a plus de forces de gravitation en Relativité Générale puisque cette déformation de l'Espace-temps en tient lieu.

Tab est le Tenseur Energie-impulsion qui décrit la distribution locale des contraintes issues de la matière et de l'énergie, ou de tout autre forme de champ non gravitationnel comme par exemple le champ électromagnétique.
Ce Tenseur dépend de la pression p et de la densité ρ du milieu physique qui emplit l'espace.
Ce Tenseur est construit de telle manière que sa Divergence nulle exprime la conservation locale de l'énergie et de l'impulsion.

Rab est le Tenseur de Ricci, obtenu par Contraction du Tenseur de courbure.

R est la Courbure scalaire, obtenue par Contraction du Tenseur de Ricci

a et b sont les indices représentatifs des lignes et des colonnes de tous les Tenseurs d'ordre 2 dans l'équation d'Einstein. Ces indices vont de 0 à 3 correspondant chacun à une dimension de l'espace-temps avec 0 pour le temps.

K est le coefficient de couplage gravitationnel. Il vaut : K = 8 π G c^-4 = 2,0766 10^-43 N^-1 ou kg^-1.m^-1.s²
Ce coefficient a été choisi de façon à vérifier l'Equation de Poisson de la gravitation Newtonienne comme cas particulier de l'équation d'Einstein (voir Limite Newtonienne).
K représente une "élasticité" de l'Espace-temps extraordinairement petite. Pour exemple, un observateur situé à la surface du Soleil (M_soleil = 1,99 10³⁰ kg ; R_soleil = 6,96 10⁸ m ; dimension n = 3) verrait l'Espace-temps se courber selon une courbure scalaire R = -K ρ c² = -K M_soleil (3/4)(1/π) R_soleil^-3 c² = -3,0 10^-24 m^-2, correspondant à un rayon de courbure r = (n(n - 1)/|R|)^1/2 = 1,0 10¹² m, soit environ 2000 fois le rayon du Soleil.

G est la constante de gravitation universelle (G = 6,67408 10^-11 kg^-1.m³.s^-2).

c est la vitesse de la lumière dans le vide (c = 2,99792458 10⁸ m.s^-1).

Λ est la Constante cosmologique de dimension m^-2 et pouvant être négative, nulle ou positive.
Le problème du mouvement des planètes, considérées comme des particules matérielles dans un espace vide autour du soleil (Espace-temps de Schwarzschild), se résoud en prenant Λ = 0 et Tab = 0. Alors qu'en cosmologie, pour déterminer le modèle d'univers (Espace-temps de Friedmann-Lemaître-Robertson-Walker), on prend a priori une valeur Λ non nulle et on considère l'espace universel comme empli d'un véritable gaz de galaxies de densité ρ et de pression p = 0 (Modèle cosmologique standard).

Equation présentée différemment

Cette équation est parfois présentée avec le signe "moins" devant Λ et/ou K.
Cela dépend des conventions d'auteurs prises pour la Signature du Tenseur métrique, la définition du Tenseur de courbure et la définition du Tenseur de Ricci.

Equation équivalente

En contractant l'équation d'Einstein par le Tenseur métrique inverse g^ab, la Courbure scalaire R est liée au Tenseur Energie-impulsion Tab par la relation :
    (E2) R = -K T + 4 Λ
où T est la trace du Tenseur Energie-impulsion : T = g^ab Tab = T^aa
En reportant cette relation dans l'équation d'Einstein (E1), on trouve l'équation équivalente suivante :

Cette équation équivalente peut être plus pratique dans certains cas, par exemple lorsqu'on s'intéresse à la limite de champ gravitationnel faible et qu'on peut remplacer gab par la Métrique de Minkowski sans perte significative de précision.
Dans le cas particulier où Tab = 0 (espace vide) et Λ = 0, le Tenseur de Ricci Rab est nul.
Une solution de l'Equation d'Einstein du vide avec Λ = 0, comme la solution de Schwarzschild, est donc une Métrique dont le Tenseur de Ricci est identiquement nul. Par contre, le Tenseur de courbure n'est pas nul, sauf dans le cas de la solution triviale constituée par la Métrique de Minkowski (Espace-temps plat de la Relativité Restreinte). cf [GOU, Relativité générale, p.119].

Propriétés de l'équation d'Einstein

3.3. Résolution de l'équation d'Einstein ( Sous-paragraphe Précédent / Suivant )

Les 16 composantes du tenseur d'Einstein modifié Sab sont fonction uniquement des potentiels de gravitation gab et de leurs dérivées première et seconde. Ces composantes sont linéaires par rapport aux dérivées secondes et font intervenir les Symboles de Christoffel fonction de ces gab.
La résolution de ces équations différentielles couplées du second ordre est extrêmement ardue.
La Symétrie des Tenseurs Rab, gab et Tab réduit à 10 le nombre d'équations distinctes et les 4 conditions de Divergence nulle liées au Tenseur Tab les ramènent à 6 équations indépendantes.
De leur côté, par symétrie, 10 seulement des gab sont distincts et, dans un quadri-espace, on peut choisir en chaque point arbitrairement les valeurs de 4 d'entre eux, ce qui réduit à 6 également le nombre des fonctions gab à déterminer.

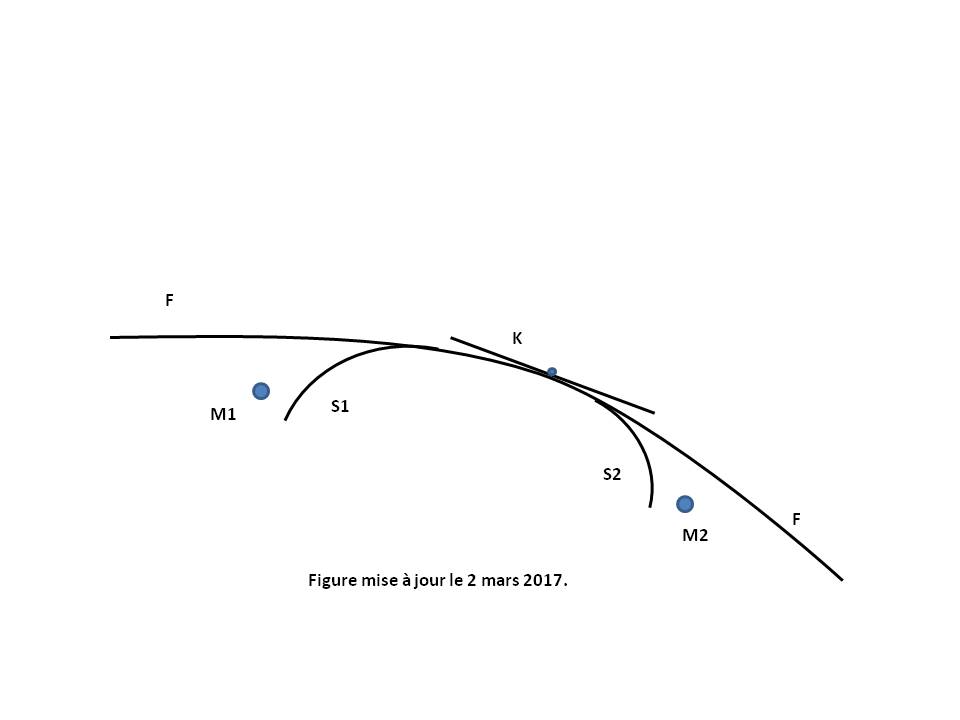
Plusieurs Métriques relativistes sont ensuite disponibles en Relativité Générale (voir Figure ci-dessus).
La Métrique de Schwarzschild (S1, S2...) décrit la géométrie autour des masses (M1, M2...), ces masses pouvant être une étoile, une planète ou un Trou noir.
La Métrique de Friedmann-Lemaître-Robertson-Walker (F) est utilisée en cosmologie pour décrire l'évolution de l'univers aux grandes échelles. Elle constitue l'outil principal amenant la construction du Modèle cosmologique standard : la théorie du Big Bang.
La Métrique de Minkowski (K) décrit la géométrie loin des masses importantes, sur la partie asymptotiquement plate des métriques précédentes, selon un Espace-temps euclidien tangent de la Relativité Restreinte.

3.4. Résolution de l'équation d'Einstein avec la Métrique de Schwarzschild ( Sous-paragraphe Précédent / Suivant )

Définition

En faisant l'hypothèse que le champ gravitationnel des corps est statique et à symétrie centrale (Métrique de Schwarzschild), comme c'est le cas pour le Soleil et de nombreux astres, alors les potentiels de gravitation gab s'expriment en coordonnées sphériques (r, θ, φ) en fonction de deux paramètres μ et α fonctions uniquement de r.
Ces gab permettent de calculer les composantes du Tenseur de Ricci (Rab) puis, par Contraction, la Courbure scalaire (R). Voir calculs détaillés ci-après.

Dans le cas particulier d'un champ de gravitation dans le vide (c'est-à-dire pour un Tenseur Energie-impulsion (Tab) nul) et d'une Constante cosmologique nulle (Λ = 0), alors l'équation d'Einstein se réduit à un système de deux équations différentielles des fonctions μ et α. Leur intégration donne les expressions de μ et α. Voir calculs détaillés ci-après.
Finalement, la Métrique de Schwarzschild ds² se détermine complètement comme suit :

où r^* est une constante appelée rayon de Schwarzschild ou rayon gravitationnel.

Dans le cas particulier d'un champ de gravitation créé par une masse M centrale symétrique, on a : r^* = 2 G M c^-2, obtenu en comparant le g00 de Schwarzschild avec le g00 de la Limite Newtonienne. Dans le cas du Soleil (avec M_Soleil = 1,9891 10³⁰ kg), r* est très petit et vaut : 3,0 km
Les valeurs particulières r = 0 et r = r^*, qui rendent infini les coefficients g00 et g11, délimitent une région singulière qui se trouve en pratique située profondément à l'intérieur de la masse M, ce qui n'est pas gênant pour les planètes, étoiles ordinaires et étoiles à neutrons pour lesquelles on a toujours : r >> r*.
Pour les Trous noirs, la singularité r = r^* peut être éliminée par un choix convenable du système de coordonnées. En revanche, la singularité r = 0 est une singularité du Tenseur métrique g qui marque la limite de la description des Trous noirs par la Relativité Générale et nécessite sans doute de recourir à une théorie quantique de la gravitation qui n'existe pas encore vraiment à ce jour.
Lorsque r tend vers l'infini, les coefficients gab se réduisent aux composantes de la Métrique de Minkowski exprimée en coordonnées sphériques. L'espace-temps de Schwarzschild est donc asymptotiquement plat.

Pour finir, on écrit et on résoud les équations de Géodésiques qui décrivent le mouvement des particules libres dans l'espace considéré, c'est-à-dire lorsque ces particules (systèmes matériels ou photons) ne sont pas soumises à une force externe autre que la gravitation dans le cadre de la Relativité Générale. Voir Géodésique d'un corps matériel et Géodésique d'un photon.

Démonstration

3.5. Résolution de l'équation d'Einstein avec la Métrique de Friedmann-Lemaître-Robertson-Walker ( Sous-paragraphe Précédent / Suivant )

Equations de Friedmann

En faisant l'hypothèse que l'Espace-temps est spatialement homogène et isotrope (Métrique de Friedmann-Lemaître-Robertson-Walker), alors les potentiels de gravitation gab s'expriment en coordonnées sphériques (r, θ, φ) en fonction de deux paramètres k (constante) et a (fonction de t uniquement).
Ces gab permettent de calculer les composantes du Tenseur de Ricci (Rab) puis, par Contraction, la Courbure scalaire (R).
En faisant ensuite le choix d'un modèle Fluide Parfait pour le Tenseur Energie-impulsion (Tab), on calcule ses composantes en fonction de la pression p et de la densité ρ du milieu physique qui emplit l'espace.
L'équation d'Einstein se réduit alors à un système de deux équations différentielles des fonctions a(t), ρ(t) et p(t), appelées équations de Friedmann :
    (F1) (a'/a)² + k (c/a)² = (1/3) ρ K c⁴ + (1/3) Λ c²
    (F2) a"/a = -(1/6) (ρ + 3 p c^-2) K c⁴ + (1/3) Λ c²
On complète le système en se donnant une équation d'état du fluide cosmique de type p = p(ρ). Un exemple d'équation d'état souvent utilisé est : p(t) = w ρ(t) c² où w est une constante qui vaut -1 (vide quantique), 0 (pression nulle) ou 1/3 (radiation électromagnétique).
Cette équation d'état, associée aux deux équations (F1) et (F2), donne une relation remarquable liant ρ(t) et a(t) :
    (Q0) ρ(t) a(t)^{3(1 + w)} = ρ₀ a₀^{3(1 + w)} = constante
    où ρ₀ et a₀ sont deux constantes (l'indice 0 correspondant généralement aux données actuelles).
Le système se réduit alors à une seule équation différentielle de la fonction a(t) (voir calculs détaillés ci-après) :

Cette équation différentielle s'intègre analytiquement pour w = -1, 0 ou 1/3 (avec Λ et k quelconques), ce qui détermine complètement a(t) et la métrique ds² comme suit :

La première équation de Friedmann (F1) est présentée souvent sous la forme condensée :
    1 + Ω_k = Ω + Ω_v
    avec :
H(t) = paramètre de Hubble (de dimension s^-1) = a'/a qui rend compte de l'expansion de l'univers. Voir Loi de Hubble-Lemaître.
Ω_k(t) = courbure réduite (sans dimension) = k (c/a)² / H(t)²
Ω(t) = paramètre de densité (sans dimension) = (8/3) π G ρ(t) / H(t)²
Ω_v(t) = Constante cosmologique réduite (sans dimension) = (1/3) Λ c² / H(t)²
q(t) = paramètre de décélération (sans dimension) = -a a"/ (a')² = -1 - H'(t)/H(t)²
Il semblerait que la valeur actuelle du paramètre de décélération soit négative (a" > 0), le ralentissement dû à l'attraction de la matière étant totalement compensé par l'accélération dû à une hypothétique énergie Noire.

La seconde équation de Friedmann (F2) s'écrit également sous la forme :
    (Q2) a"/a = -F a^{-3(1 + w)} + B
    (Q2a) F = (1/2) (1 + 3 w) A
A noter que la relation (Q2) s'obtient également immédiatement par dérivation de la relation (Q1).

Allure générale des courbes a(t)

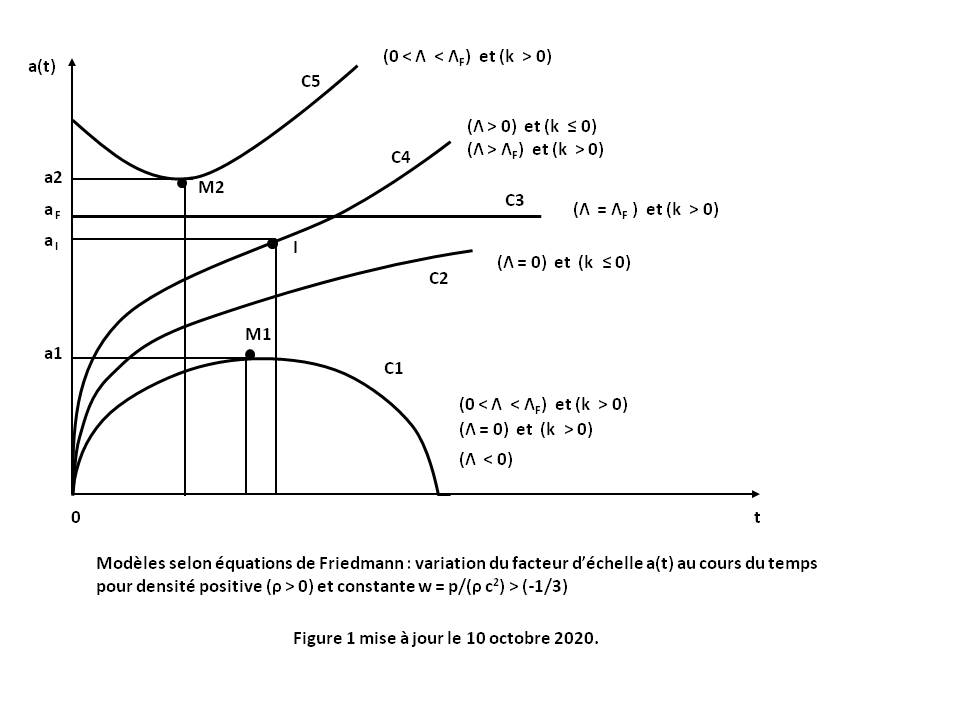
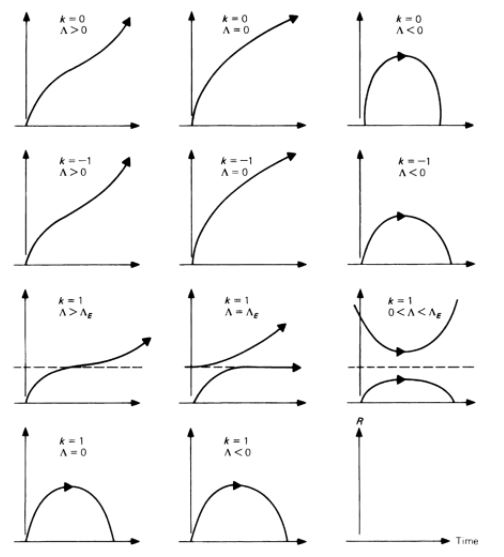
Dans le cas standard où ρ > 0 et w > (-1/3), on déduit alors des relations (Q1) et (Q2) l'allure générale des courbes a(t) pour Λ et k quelconques (voir Figure 1 ci-dessus avec Démonstration ci-après, ou Figure 2 ci-dessus cf [HAR Cosmology, tableau p.367] ou [LUM, tableau p.153]).
Toutes ces courbes, sauf deux, représentent des modèles avec Big Bang pour lesquels a(t) tend vers 0 lorsque t tend vers 0 :
- La courbe C1 relative au cas (Λ < 0), ou au cas (Λ = 0) et (k > 0), correspond à un modèle fermé (expansion décélérée avec un point maximum M1).
- La courbe C2 relative au cas (Λ = 0) et (k ≤ 0) correspond à un modèle ouvert (expansion décélérée).
- La courbe C4 relative au cas (Λ > 0) et (k ≤ 0), ou au cas (Λ > Λ_F) et (k > 0), correspond à un modèle ouvert à point d'inflexion I (expansion décélérée puis accélérée). Le sous-cas (Λ > 0) et (k = 0) correspond au Modèle cosmologique standard quand la pression est nulle (w = 0).
- Les courbes C5, et C1 à nouveau, sont relatives au cas (0 < Λ < Λ_F) et (k > 0). Elles correspondent à deux comportements possibles : un modèle ouvert de type non Big Bang (expansion accélérée avec un point minimum M2), et un modèle fermé avec un point maximum M1.
- La courbe C3 est relative au cas singulier (Λ = Λ_F) et (k > 0). Elle correspond à un modèle statique (Univers statique d'Einstein) pour lequel a(t) = constante. Ce modèle est instable aux perturbations de densité ρ avec une tendance locale à l'expansion (courbe C5 après le point M2) ou à la contraction (courbe C1 avant le point M1).
A noter que ces courbes représentent un sous-ensemble de courbes répertoriées par Harrison [HAR Classification].

Λ_F est la Constante cosmologique singulière de Friedmann qui s'écrit (voir Démonstration ci-après) :
    (Q6) Λ_F = (1/2)(1 + 3 w) ρ_F K c²
    (Q6a) a_F = ( (1/2)(1/k)(1 + w) ρ_F K c² )^-1/2
Pour k = 1 et ρ_F = ρ_E, on obtient les expressions Λ_E et a_E de l'Univers statique d'Einstein :
    Λ_E = (1/2)(ρ_E + 3 p_E c^-2) K c²
    a_E = ( (1/2)(ρ_E + p_E c^-2) K c² )^-1/2

Solutions simples pour a(t)

Certaines solutions particulièrement simples pour a(t) sont présentées ci-dessous (l'indice 0 correspondant généralement aux données actuelles).
Hormis les deux premières solutions, les autres sont presque toutes des modèles avec Big Bang présentées selon les valeurs des paramètres w, puis Λ puis k.

1. Univers statique d'Einstein
C'est le modèle cosmologique statique avec : a(t) = a_E ; ρ(t) = ρ_E ; p(t) = p_E
où a_E, ρ_E et p_E sont des constantes.
La seconde équation de Friedmann (F2) devient alors : Λ = Λ_E
avec : Λ_E = (1/2)(ρ_E + 3 p_E c^-2) K c²
Λ_E est la Constante cosmologique singulière d'Einstein qui caractérise un univers statique.
A noter qu'en dehors du vide (ρ_E = p_E = 0), une solution statique ne peut exister qu'avec une Constante cosmologique non nulle.
En reportant cette valeur de Λ dans la première équation de Friedmann (F1), on obtient :
    k /a_E² = (1/2)(ρ_E + p_E c^-2) K c²
Si le fluide cosmique satisfait à la condition d'énergie faible au sens strict, alors on a : ρ_E + p_E c^-2 > 0 et donc nécessairement : k > 0, donc : k = 1
La courbe a(t) est une constante (voir courbe C3 en Figure 1 ci-dessus) :
    a(t) = a_E = ( (1/2)(ρ_E + p_E c^-2) K c² )^-1/2

2. Espace-temps de De Sitter
C'est le modèle cosmologique du vide (ρ = p = 0) avec Λ > 0 et k = 0 (courbure plate).
La première équation de Friedmann (F1) devient alors : (a'/a)² = (H0)²
    avec H0 = B^1/2 = c (Λ / 3)^1/2
Cette équation s'intègre en :
    a(t) = a₀ e^{H0 (t - t0)}
    où a₀ et t0 sont des constantes.
La courbe a(t) est de type exponentielle et n'est pas un modèle avec Big Bang.

3. Modèle de Friedmann avec courbure ouverte
C'est le modèle cosmologique sans pression (w = 0) avec Λ = 0 et k = -1 (courbure ouverte)
En remplaçant ces valeurs dans l'équation différentielle (Q1), on trouve :
    a'² = A a^-1 + c²
    avec A = A(w = 0) selon la relation (Q1a)
Cette équation s'intègre sous forme d'une équation paramétrique :
    a(t) = D (cosh[m] - 1)
    t - ti = (D/c) (sinh[m] - m)
    avec D = (1/2) A c^-2 et paramètre m > 0
    où a₀, ρ₀ > 0 et ti sont des constantes, ti étant généralement fixée à 0 par un choix d'origine de la coordonnée t.
Le terme (t - ti) s'exprime plus simplement en fonction de (a) sous la forme :
    t - ti = (D/c) ( ((a/D)(2 + (a/D)))^1/2 - ln[ (1 + (a/D)) + ((a/D)(2 + (a/D)))^1/2 ] )
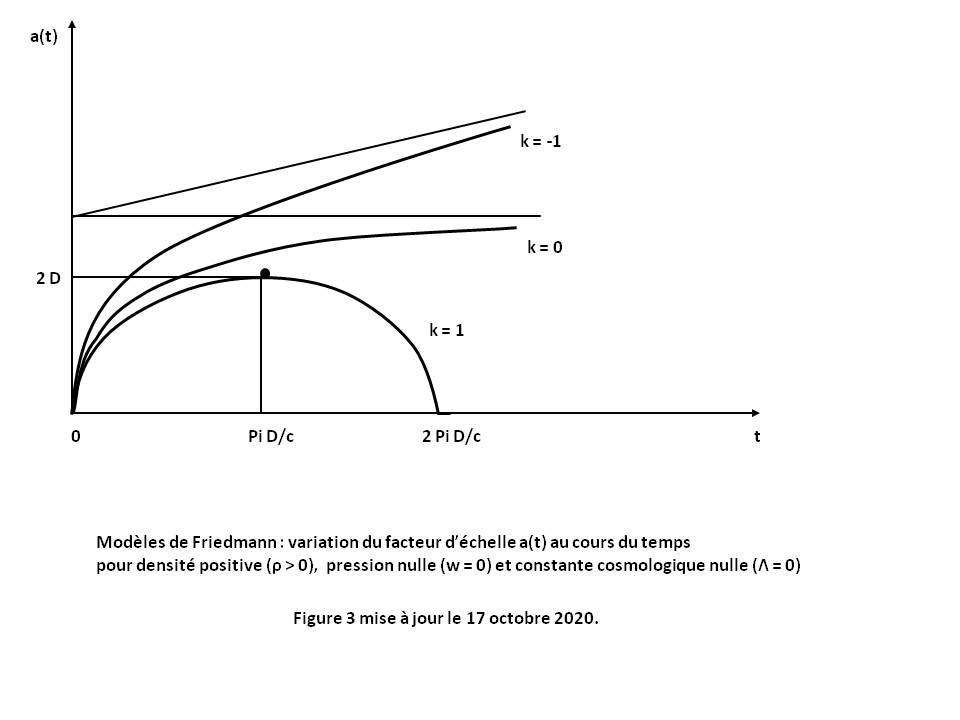
La courbe a(t) est de type hyperbolique (voir Figure 3 ci-dessus pour k = -1).

4. Modèle de Friedmann avec courbure plate (ou Espace-temps d'Einstein-De Sitter)
C'est le modèle cosmologique sans pression (w = 0) avec Λ = 0 et k = 0 (courbure plate)
En remplaçant ces valeurs dans l'équation différentielle (Q1), on trouve :
    a'² = A a^-1
    avec A = A(w = 0) selon la relation (Q1a)
Cette équation s'intègre en :
    a(t) = ( (1/j) A^1/2 (t - ti) )^j
    avec j = 2/3
    où a₀, ρ₀ > 0 et ti sont des constantes, ti étant généralement fixée à 0 par un choix d'origine de la coordonnée t.
La courbe a(t) est une fonction puissance (voir Figure 3 ci-dessus pour k = 0).

5. Modèle de Friedmann avec courbure fermée
C'est le modèle cosmologique sans pression (w = 0) avec Λ = 0 et k = 1 (courbure fermée)
En remplaçant ces valeurs dans l'équation différentielle (Q1), on trouve :
    a'² = A a^-1 - c²
    avec A = A(w = 0) selon la relation (Q1a)
Cette équation s'intègre sous forme d'une équation paramétrique :
    a(t) = D (1 - cos[m])
    t - ti = (D/c) (m - sin[m])
    avec D = (1/2) A c^-2 et paramètre m variant de 0 à 2 π
    où a₀, ρ₀ > 0 et ti sont des constantes, ti étant généralement fixée à 0 par un choix d'origine de la coordonnée t.
Le terme (t - ti) s'exprime plus simplement en fonction de (a) sous la forme :
    Pour t - ti < π (D/c) : t - ti = (D/c) ( Arccos[1 - (a/D)] - ((a/D)(2 - (a/D)))^1/2 )
    Pour t - ti > π (D/c) : t - ti = 2 π (D/c) - (expression (t - ti) du cas précédent)
La courbe a(t) est une cycloïde (point d'un cercle roulant sur une droite). Elle est symétrique par rapport à la valeur t - ti = π (D/c) (voir Figure 3 ci-dessus pour k = 1).
On notera que la courbe va du "Big Bang" (t - ti = 0) au "Big Crunch" (t - ti = 2 π (D/c)) en passant par une phase d'expansion (a' > 0) puis par une phase de contraction (a' < 0).

6. Modèle sans pression (w = 0) avec Λ non nul
La solution exacte de ce modèle est donnée par [KHA Some_exact_solutions].

7. Modèle sans pression (w = 0) avec Λ non nul et k = 0 (courbure plate)
En remplaçant ces valeurs dans l'équation différentielle (Q1), on trouve :
    a'² = A a^-1 + B a²
    avec A = A(w = 0) et B donnés par les relations (Q1a) et (Q1b)
Cette équation s'intègre en :
    si Λ < 0 : a(t) = (-A/B)^1/3 sin^2/3[ (3/2) (-B)^1/2 (t - ti) ]
    si Λ > 0 : a(t) = (A/B)^1/3 sinh^2/3[ (3/2) B^1/2 (t - ti) ]
    où a₀, ρ₀ > 0 et ti sont des constantes, ti étant généralement fixée à 0 par un choix d'origine de la coordonnée t.
Si Λ < 0, la courbe a(t) est similaire à la courbe fermée du modèle de Friedmann (voir Figure 3 ci-dessus pour k = 1).
Si Λ > 0, la courbe a(t) comporte deux phases d'expansion successives (a' > 0). La première phase est similaire à la courbe ouverte du modèle de Friedmann (voir Figure 3 ci-dessus pour k = -1) avec décélération (a" < 0) mais menant à un point d'inflexion I (a" = 0). La seconde phase est à nouveau une courbe ouverte mais avec accélération (a" > 0) (voir courbe C4 en Figure 1 ci-dessus).

8. Modèle pour radiations électromagnétiques (w = 1/3) avec Λ non nul
La solution exacte de ce modèle est donnée par [KHA Some_exact_solutions].

9. Modèle pour radiations électromagnétiques (w = 1/3) avec Λ = 0
En remplaçant ces valeurs dans l'équation différentielle (Q1), on trouve :
    a'² + k c² = A a^-2
    avec A = A(w = 1/3) selon la relation (Q1a)
Cette équation s'intègre en :
    Pour k = -1 : a(t) = E c ( (1 + (1/E)(t - ti))² - 1 )^1/2
    Pour k = 0 : a(t) = (4 A)^1/4 (t - ti)^1/2
    Pour k = 1 : a(t) = E c ( 1 - (1 - (1/E)(t - ti))² )^1/2
    avec E = (A)^1/2 c^-2
    où a₀, ρ₀ > 0 et ti sont des constantes, ti étant généralement fixée à 0 par un choix d'origine de la coordonnée t.
Les courbes a(t) sont similaires aux courbes du modèle de Friedmann (voir Figure 3 ci-dessus pour k = -1, 0 et 1).

10. Modèle avec w > (-1/3), Λ = 0 et k = 0 (courbure plate)
En remplaçant ces valeurs dans l'équation différentielle (Q1), on trouve :
    a'² = A a^{-(1 + 3 w)}
    avec A = A(w) selon la relation (Q1a)
Cette équation s'intègre en :
    a(t) = ( (1/j) A^1/2 (t - ti) )^j
    avec j = (2/3) (1 + w)^-1 < 1
    où a₀, ρ₀ > 0 et ti sont des constantes, ti étant généralement fixée à 0 par un choix d'origine de la coordonnée t.
La courbe a(t) est une fonction puissance ayant une branche parabolique selon l'axe des temps quand t temps vers l'infini (voir Figure 3 ci-dessus pour k = 0).

Démonstrations

3.6. Décalages spectraux ( Sous-paragraphe Précédent / Début )

La Relativité Générale explique avec succès trois types de décalages spectraux fondamentaux [AND Théorie - Partie 2] :

L'Effet Doppler-Fizeau qui induit un décalage spectral dû à un effet de vitesse de la source lumineuse par rapport à l'Observateur.
Ce décalage est dirigé indifféremment vers le bleu ou le rouge suivant que la vitesse est une vitesse d'approche ou d'éloignement mais dont l'effet transversal est toujours dirigé vers le rouge.

L'Effet Einstein qui induit un décalage spectral d'origine gravitationnel dû à l'effet d'une masse proche de la source.
Un rayonnement émis dans un champ gravitationnel intense est observé avec un décalage qui est toujours dirigé vers le rouge.

La Loi de Hubble-Lemaître qui induit un décalage spectral cosmologique dû à un effet de distance de la source.
Ce décalage est toujours dirigé vers le rouge.

Pour expliquer ces phénomèmes très profonds de la physique, la Relativité Générale a dù passer par les généralisations successives de la notion d'Espace-temps :
- L'espace-temps plat pour interpréter l'Effet Doppler-Fizeau.
- L'espace-temps courbe pour interpréter l'Effet Einstein.
- L'espace-temps à courbure variable pour interpréter la Loi de Hubble-Lemaître.

4. Lexique ( Paragraphe Précédent / Suivant )

Le Lexique ci-dessous détaille les termes et notions utilisés dans cette page, listés par ordre alphabétique.

1. Abaissement d'indice
2. Aberration de la lumière
3. Age de l'univers
4. Antisymétrie et symétrie
5. Base (changement)
6. Base directe (et indirecte)
7. Base naturelle
8. Base orthonormée
9. Big Bang
10. Comobilité
11. Cône de lumière
12. Constante cosmologique
13. Constante de structure de l'espace-temps
14. Contraction des indices (ou trace d'un tenseur)
15. Contraction des longueurs (ou contraction de FitzGerald-Lorentz)
16. Convention de dérivée partielle
17. Conventions de signe MTW
18. Convention de sommation (dite "convention d'Einstein")
19. Courbure
20. Courbure scalaire (ou invariant scalaire)
21. Covariance d'une loi physique (ou principe de Relativité Générale)
22. Covariance et contravariance
23. Dérivée covariante (ou gradient)
24. Dérivée partielle (convention)
25. Dilatation des durées (ou Ralentissement des horloges mobiles)
26. Dilatation du temps gravitationnel
27. Divergence
28. Dual (espace et base)
29. Effet Doppler (ou Doppler-Fizeau)
30. Effet Einstein (ou décalage spectral gravitationnel ou effet Doppler gravitationnel)
31. Effet Shapiro (ou retard de la lumière)
32. Elévation d'indice
33. Energie et impulsion d'une particule mesurés par un observateur
34. Equation d'Einstein
35. Equation de Poisson
36. Equations de Friedmann
37. Equations de Maxwell
38. Espace-temps
39. Espace local de repos de l'observateur
40. Facteur de Lorentz
41. Forme linéaire
42. Genre d'un vecteur
43. Géodésique
44. Géodésique d'un corps matériel
45. Géodésique d'un photon
46. GPS
47. Histoire de l'univers
48. Image d'un objet en mouvement
49. Ligne d'univers
50. Limite Newtonienne
51. Loi de composition des vitesses
52. Loi de Hubble-Lemaître
53. Mécanique relativiste
54. Métrique de Friedmann-Lemaître-Robertson-Walker (ou métrique FLRW)
55. Métrique de Minkowski
56. Métrique de Schwarzschild
57. Métrique relativiste
58. Mirage gravitationnel (ou lentille gravitationnelle)
59. Modèle cosmologique standard
60. Modèle standard de la physique des particules
61. Moment cinétique d'une particule mesuré par un observateur
62. Multiplicité des temps propres (ou Désynchronisation des horloges parfaites)
63. Noire (énergie)
64. Noire (matière)
65. Notations mathématiques
66. Observateur
67. Onde gravitationnelle
68. Opérateurs élémentaires sur les tenseurs
69. Paradoxe des jumeaux (ou paradoxe des horloges ou voyageur de Langevin)
70. Principe d'équivalence
71. Produit scalaire et norme
72. Produit tensoriel
73. Produit vectoriel
74. Quadri-accélération
75. Quadri-courant électrique
76. Quadri-force
77. Quadri-impulsion
78. Quadri-position
79. Quadri-potentiel électromagnétique
80. Quadri-rotation
81. Quadri-vecteur
82. Quadri-vitesse
83. Référentiel céleste et Référentiel terrestre
84. Référentiel inertiel (ou galiléen)
85. Référentiel local
86. Signature
87. Simultanéité
88. Sommation (convention)
89. Symboles de Christoffel
90. Symbole de Kronecker
91. Symbole de Levi-Civita
92. Symétrie et antisymétrie
93. Temps cosmique
94. Temps et Durée
95. Temps standard
96. Tenseur
97. Tenseur d'Einstein
98. Tenseur d'Einstein modifié
99. Tenseur de courbure (ou de Riemann-Christoffel)
100. Tenseur de Levi-Civita
101. Tenseur de Ricci
102. Tenseur électromagnétique (ou tenseur de Maxwell ou tenseur de Faraday)
103. Tenseur Energie-Impulsion
104. Tenseur Energie-Impulsion du champ ElectroMagnétique
105. Tenseur Energie-Impulsion du Fluide Parfait
106. Tenseur métrique (ou fondamental)
107. Tensorialité (critères)
108. Trajectoire
109. Transformation de Galilée
110. Transformation de Lorentz-Poincaré
111. Trou de ver
112. Trou noir

Abaissement d'indice

Un indice supérieur peut être changé en un indice inférieur par multiplication avec le Tenseur métrique gij puis Contraction des indices. Exemples :
Uik = gij U^jk
Ulm = gjl gkm U^jk
U^klm = glp U^kpm
Attention : Si on garde la même lettre pour le tenseur résultat (après suppression des indices identiques), alors la notation peut devenir ambigüe (voir Contraction des indices).

Aberration de la lumière

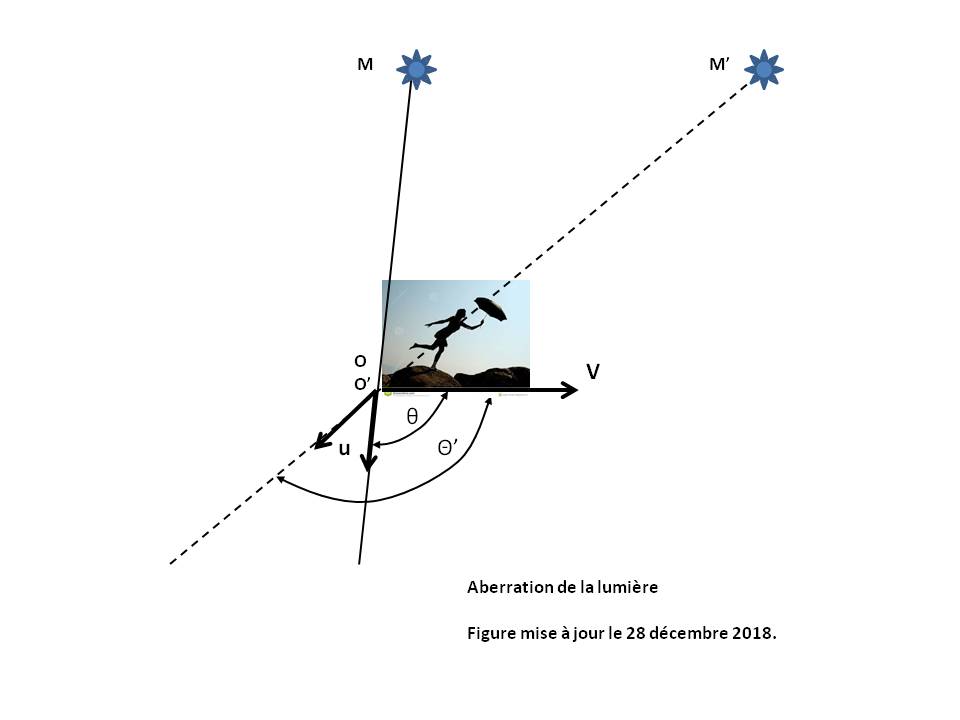
Figure 1 ci-dessus : Phénomème d'aberration lumineuse
Figure 2 ci-dessus : Distorsion de la sphère céleste. Les quatre images correspondent à différentes valeurs de la vitesse v de l'observateur mobile O' (v = 0 ; 0.3 c ; 0.6 c ; 0.9 c) [GOU, Relativité Restreinte, p.162].

L'aberration de la lumière est la différence entre les directions d'incidence d'un même rayon lumineux perçues par deux Observateurs en mouvement relatif.
Il ne s'agit pas d'un effet purement relativiste car l'aberration résulte du temps fini de propagation d'un signal, comme le montre l'exemple du piéton qui marche sous la pluie : la pluie tombant verticalement par rapport au sol, le piéton doit incliner son parapluie vers l'avant s'il ne veut pas être mouillé.
Soit O un Observateur d'un référentiel R et O' un Observateur d'un référentiel R' en translation rectiligne uniforme de vitesse v par rapport à R.
Dans le cas d'une source lumineuse M vue par O', la lumière émanant de M semble provenir de M' et non de M (voir Figure 1 ci-dessus).

u est le vecteur unitaire de la propagation lumineuse MO.
Si la propagation lumineuse u fait avec la vitesse v un angle θ dans R et θ' dans R', alors on a la relation :

    cos[θ'] = (cos[θ] - v/c) / (1 - cos[θ] v/c)

En utilisant la relation : tan²[θ/2] = (1 - cos[θ])/(1 + cos[θ]), on a la relation équivalente :

On a donc toujours : θ' > θ, comme si la lumière reçue par l'Observateur mobile se concentrait vers sa direction de déplacement.
- Lorsque la propagation u est parallèle à la vitesse v dans le référentiel R (θ = 0 ou π), alors la formule se réduit à : cos[θ'] = 1 ou -1, ce qui induit : θ' = 0 ou π, et il n'y a pas d'effet d'aberration.
- Lorsque u est perpendiculaire à v dans le référentiel R (θ = π/2), alors la formule se réduit à : cos[θ'] = -v/c, ce qui induit : θ' > π/2 (et le piéton doit incliner son parapluie vers l'avant).
    Pour un Observateur terrestre O' (v = 30 km.s^-1), l'Image d'une étoile située au pôle nord de l'écliptique (θ = π/2) décrit ainsi en une année un cercle de rayon 20'' autour de ce pôle. A ne pas confondre avec la parallaxe qui est l'angle de vue d'une étoile lorsque la Terre parcours son orbite et qui vaut au maximum 0.77'' pour l'étoile la plus proche (Proxima Centauri) [GOU, Relativité Restreinte, p. 162].
- Lorsque v est petit devant c, il n'y a pas d'effet d'aberration (θ' = θ).

Le phénomème d'aberration se visualise très bien en considérant une grille uniforme sur la sphère céleste de l'Observateur O (voir Figure 2 ci-dessus). L'Observateur O' voit apparaître dans son champ de vision des directions qui étaient hors champ pour l'Observateur O, jusqu'à voir les deux pôles célestes en même temps.
L'aberration relativiste de la lumière a été démontrée directement par l'équipe de Daniel Giovannini de l'Université de Glasgows, en laboratoire terrestre.

Age de l'univers

L'âge de l'univers est la durée écoulée depuis le Big Bang. La meilleure approximation actuelle est donnée par : 1 / H0
où H0 est la constante de Hubble (voir Loi de Hubble-Lemaître),
ce qui donne un âge d'environ 13 milliards d'années.

Antisymétrie et symétrie

Voir Symétrie et antisymétrie.

Base (changement)

Soit [A] la matrice de passage de la base {ei} à la base {e'k} telle que : e'k = Aⁱk ei, et [B] = [A^-1] la matrice de passage inverse telle que : ei = Bⁱk e'k
Pour un tenseur quelconque T d'ordre 2, en utilisant la multilinéarité de T et les propriétés de Covariance et contravariance, les composantes du tenseur T' sont données par les lois suivantes :
T'ij = A^ki A^lj Tkl
T' ^ij = Bⁱk B^jl T^kl
T' ⁱj = Bⁱk A^lj T^kl
Le changement de base transforme le tenseur T en un tenseur T' dont les composantes sont des combinaisons linéaires des composantes du tenseur origine.

Pour un tenseur quelconque T p fois contravariant et q fois covariant, la loi générale de transformation est la suivante [GOU, Relativité Restreinte, p. 476] :

Base directe (et indirecte)

Si ei sont les vecteurs de base de l'Espace-temps, la base {ei} est dite [GOU, Relativité Générale, p.21] :

où Ε est le Tenseur de Levi-Civita.

Base naturelle

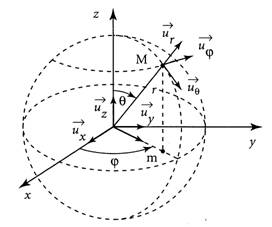
En tout point M de coordonnées (x⁰, x¹, x², x³) de l'Espace-temps, la base naturelle associée au point M est l'ensemble des vecteurs ui vérifiant la relation suivante [GOU, Relativité Restreinte, p.492] [GOU, Relativité Générale, p.19] :

ui décrit ainsi l'accroissement de la coordonnée xⁱ au voisinage de M (voir Figure ci-dessus) et se note vectoriellement : ui = d/d(xⁱ). A ne pas confondre avec l'opérateur dérivée partielle.

Propriétés :
- Les vecteurs ui constituent une base vectorielle de l'Espace-temps.
- Chaque vecteur ui est en fait un champ de vecteurs qui peut s'écrire :

Les vecteurs ur, uθ et uφ ne constituent pas une Base orthonormée de R³ pour le produit scalaire euclidien usuel.
La base orthonormée associée (appelée "base naturelle normalisée") s'écrit : (ur, r^-1 uθ, (r sin[θ])^-1 uφ).

Base orthonormée

Si ei sont les vecteurs de base de l'Espace-temps, la base {ei} est dite orthonormée (relativement au Produit scalaire g) lorsque [GOU, Relativité Générale, p.26] :

La matrice [gij] de cette base particulière, notée [ηij], est appelée matrice de Minkowski et correspond à l'Espace-temps de la Relativité Restreinte en coordonnées cartésiennes.

Big Bang

Définition :
Le Big Bang est un mot ayant une double signification :
- Evénement marquant le début de l'expansion de l'univers, sans que cela préjuge de l'existence d'un "instant initial" ou d'un commencement à son histoire.
- Modèle cosmologique standard décrivant l'évolution de l'univers, depuis un état infiniment dense et incroyablement chaud (10¹³ °C) jusqu'à aujourd'hui.
Le Big Bang, appelé abusivement "explosion primordiale", est en fait une "dilatation primordiale" telle que le facteur d'échelle a(t) tende vers 0 quand t tend vers 0. Il n'y a pas éjection de matière à partir d'un endroit de l'univers mais dilatation de l'espace réduit en un point, qui emmène avec lui tous les objets de l'univers.
Le Big Bang a été formulé en 1927 par Georges Lemaître et confirmé en 1965 par Arno Penzias et Robert Wilson par la découverte du fonds cosmique micro-onde représentant le rayonnement résiduel de l'univers primordial.

Chronologie simplifiée (cf [Les secrets de l'espace] et http://scphysiques.free.fr/2nde/documents/Histoire_atome/bigbang.html ) :
- Entre 0 et 10^-43 secondes après le Big Bang, correspondant à l' "ère de Planck", sorte de quantum temporel incompressible selon la physique quantique, notre physique est muette mais les scientifiques pensent qu'à la fin de cette période, la gravité s'est séparée des autres forces de la nature (force nucléaire forte, force nucléaire faible et force électromagnétique).
- Entre 10^-43 et 10^-6 secondes après le Big Bang, les scientifiques décrivent l'évolution de l'univers à partir d'hypothèses. Le Big Bang ne peut être décrit selon les équations connues de la physique qu'à partir de 10^-6 secondes.
- Environ 10^-32 secondes après le Big Bang, une des hypothèses est que l'univers était une "soupe" de particules élémentaires et d'anti-particules. Certaines existent toujours aujourd'hui sous forme de quarks, d'anti-quarks et de bosons comme les gluons. D'autres n'existent plus comme les gravitons (particules hypothétiques qui transmettent la gravité) et les bosons de Higgs qui transmettent de la masse à d'autres particules.
- 300 000 ans après le Big Bang, lorsque la température chute à environ 2700 °C, se forment les premiers atomes d'hydrogène et d'hélium. Les électrons étant alors liés aux atomes, matière et rayonnement deviennent découplés. Les photons peuvent alors voyager à travers l'univers sous forme de rayonnement. Ils atteignent la Terre non pas sous forme de lumière visible mais en tant que photons de faible énergie du fond diffus cosmologique.
- 200 millions d'années après le Big Bang, apparaissent les premières étoiles constituées presque exclusivement d'hydrogène et d'hélium. Au cours de leur vie et de leur mort, ces premières étoiles créent de nouveaux éléments chimiques à partir de la fusion nucléaire dans les noyaux chauds de ces étoiles, comme le carbone, l'oxygène, le silicone et le fer. Ces éléments chimiques sont dispersés dans l'espace et dans d'autres galaxies.
- Les secondes et troisièmes générations d'étoiles se forment plus tard dans ce milieu interstellaire enrichi. Elles créent encore plus d'éléments chimiques renvoyés dans le milieu interstellaire via les vents solaires et les explosions de supernovae.
- L'Histoire de l'univers se poursuit ensuite avec la création de notre Soleil, de la Terre et de la vie sur Terre. A noter que la Terre ne recevra jamais de lumière visible avant la combustion des premières étoiles.
- Aujourd'hui, l'univers est extrêmement peu dense (quelques atomes par mètre cube) et froid (-271 °C).

Comobilité

Deux objets matériels sont dits comobiles lorsqu'il sont fixes l'un par rapport à l'autre dans un référentiel donné. Ils partagent alors le même mouvement spatial, que ce soit en Relativité Restreinte (où ils ont la même vitesse dans un Référentiel inertiel) ou en Relativité Générale (où ils suivent des Géodésiques parallèles dans l'Espace-temps courbé).

Cône de lumière

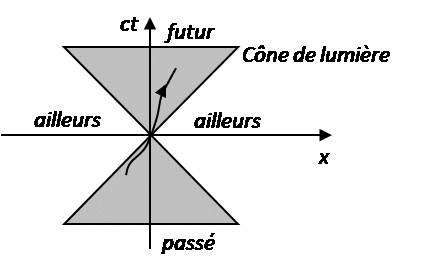
Le cône de lumière est une notion fondamentale de la Relativité Restreinte, permettant la distinction entre un événement passé, un événement futur et un événement inaccessible (dans le passé ou dans le futur).
Si un signal lumineux part du point origine O pour aller au point M de coordonnées (x, y, z), alors le lieu des trajectoires des rayons lumineux issu de O dans l'Espace-temps sera un hypercône d'équation : c² t² = x² + y² + z², appelé Cône de lumière (voir Figure ci-dessus, pour laquelle x représente de façon simplifiée les trois coordonnées spatiales x, y et z).

Constante cosmologique

L'histoire de la Constante cosmologique Λ est particulièrement mouvementée :
- En 1915, Einstein publie son Equation de la Relativité Générale, sans constante cosmologique Λ.
- En 1917, Einstein rajoute le paramètre Λ à son Equation lorsqu'il se rend compte que sa théorie implique un univers dynamique pour lequel l'espace est fonction du temps. Il donne alors à cette constante une valeur très particulière pour forcer son modèle d'univers à demeurer statique et éternel (Univers statique d'Einstein), ce qu'il appellera plus tard "la plus grande bêtise de sa vie".
- En 1922, le physicien russe Alexander Friedmann montre mathématiquement que l'Equation d'Einstein (avec Λ quelconque) reste valide dans un univers dynamique.
- En 1927, l'astrophysicien belge Georges Lemaître montre que l'univers est en expansion en combinant la Relativité Générale avec certaines observations astronomiques, celles de Hubble notamment.
- En 1931, Einstein accepte finalement la théorie d'un univers en expansion et propose, en 1932 avec le physicien et astronome hollandais Willem de Sitter, un modèle d'univers en expansion continu à constante cosmologique nulle (Espace-temps d'Einstein-De Sitter).
- En 1998, deux équipes d'astrophysiciens menées, l'une par Saul Perlmutter, l'autre par Brian Schmidt et Adam Riess, réalisent des mesures sur de lointaines supernovae et montrent que la vitesse de récession des galaxies par rapport à la Voie lactée augmente au cours du temps. L'univers est en expansion accélérée, ce qui nécessite d'avoir un Λ strictement positif. L'univers contiendrait une mystérieuse énergie Noire produisant une force répulsive qui contrebalance le freinage gravitationnel produit par la matière contenue dans l'univers (voir Modèle cosmologique standard).
    Pour ces travaux, Perlmutter (Américain), Schmidt (Américano-australien) et Riess (Américain) reçoivent conjointement le Prix Nobel de physique en 2011.
- En 2015, la valeur de la constante cosmologique est estimée à Λ = 1,11 10^-52 m^-2

Constante de structure de l'espace-temps

La constante de structure de l'espace-temps est une constante qui s'apparente à une vitesse limite de propagation des interactions. Elle apparaît au cours de la démonstration des équations de la Transformation de Lorentz-Poincaré et correspond au postulat de causalité qui garantit l'ordre temporel des événements causaux dans tous les référentiels inertiels.
Cette constante est prise égale à la plus grande vitesse mesurée actuellement qui est celle des phénomènes électromagnétiques dans le vide, en l'occurence la vitesse de la lumière dans le vide (c).

Contraction des indices (ou trace d'un tenseur)

L'opération de contraction des indices d'une composante mixte d'un Tenseur consiste à choisir deux indices, l'un covariant, l'autre contravariant, puis à les égaler et à sommer par rapport à cet indice deux fois répété.
Par exemple, pour un tenseur U d'ordre 3 dont les composantes mixtes sont U^ijk, la contraction sur les indices j et k donne le Tenseur Tⁱ = U^ikk = Uⁱ¹1 + Uⁱ²2 + ... Uⁱⁿn
Les quantités Tⁱ ainsi obtenues, composantes contractées du tenseur U, forment les composantes d'un tenseur T d'ordre 1.
A noter que l'opérateur "produit matriciel" est un cas particulier du Produit tensoriel Uⁱj ⊗ V^kl contracté sous la forme : Tⁱl = Uⁱk V^kl

Autres exemples :

Cas du Tenseur de courbure Rⁱjkl : la contraction sur les indices i et k donne le Tenseur de Ricci : Rjl = R^kjkl
Attention : Si on garde la même lettre pour le tenseur résultat (après suppression des indices identiques), alors la notation peut devenir ambigüe. Pour le Tenseur Rⁱjlk (différent de Rⁱjkl), la contraction sur les indices i et k donne le Tenseur R^kjlk = Rjl, c'est-à-dire l'opposé du Tenseur de Ricci malgré la notation identique Rjl.

Cas du Tenseur de courbure Rijkl : l'Elévation de l'indice i donne, après contraction sur les indices m et i, le Tenseur g^mi Rijkl = R^miijkl = R^mjkl
Attention : Si on garde la même lettre pour le tenseur résultat (après suppression des indices identiques), alors la notation peut devenir ambigüe. Pour le Tenseur de courbure Rjikl (différent de Rijkl), sa contraction avec g^mi donne le Tenseur g^mi Rjikl = R^mijikl = R^mjkl, c'est-à-dire l'opposé du Tenseur R^miijkl malgré la notation identique R^mjkl.

Contraction des longueurs (ou contraction de FitzGerald-Lorentz)

En Relativité Restreinte, si un bipoint de longueur propre donnée (l0) est fixe dans un référentiel, alors sa longueur dans tout autre référentiel est inférieure à la longueur propre et s'appelle longueur apparente (l).
Certains auteurs parlent à ce propos de Contraction des longueurs. Cette contraction n'est pas physique mais résulte simplement de mesures qui n'ont de sens que par rapport à un référentiel donné.
La contraction des longueurs n'intervient que dans la direction du mouvement relatif entre référentiels. Il n'y a pas de contraction dans les directions orthogonales.
Ce phénomème a été démontré indirectement par Bruno Rossi et David B. Hall via l'expérience des muons cosmiques.

Convention de dérivée partielle

Afin d'alléger les expressions des dérivées des fonctions dépendant de n variables f(x¹, x²... xⁿ), on note les dérivées partielles sous les formes suivantes :

Conventions de signe MTW

En Relativité, les conventions de signe classiques sont celles de Misner, Thorne et Wheeler [MTW, Gravitation, 1973], appellées aussi "Landau-Lipschitz Spacelike Convention" (LLSC),
avec un Tenseur métrique de Signature (-, +, +, +), un Tenseur de courbure défini par Rⁱjkl = Γⁱjl_,k + ..., et un Tenseur de Ricci défini par Rij = R^kikj
Si on définit par (C1), (C2), (C3) et (C4) les quatre signes suivants, ces auteurs classent la plupart des conventions existantes selon les trois signes indépendants (C1)(C2)(C4).
    (C1) Signature (-, +, +, +)
    (C2) Tenseur de courbure défini par Rⁱjkl = Γⁱjl_,k + ...
    (C3) Tenseur de Ricci défini par Rij = R^kikj
    (C4) "Signe d'Einstein" qui est le signe devant le second membre K Tab de l'Equation d'Einstein et correspondant à (C4) = (C2)(C3)

Ces conventions de signe classiques sont également utilisées par Caroll (Spacetime and Geometry, 2004), Hartle (Gravity, 2003), Hawking & Ellis (The large scale structure of space-time, 1973), Poisson (A Relativist's Toolkit, The Mathematics of Black-Hole Mechanics, 2004) et Gourgoulhon ([GOU, Relativité restreinte, pp 8][GOU, Relativité générale, pp 24, 109, 111]).

Convention de sommation (dite "convention d'Einstein")

Pour un espace vectoriel de dimension n ayant pour vecteurs de base l'ensemble (e1, e2... en), tout vecteur x de cet espace peut s'écrire : x = x¹ e1 + x² e2 + ... + xⁿ en = ∑_{k=1, n}[x^k ek]
Afin d'alléger cette écriture, on utilise une convention de notation consistant à supprimer le symbole "Somme", ce qui s'écrit sous forme condensée :

La sommation s'effectue sur les indices à condition toutefois qu'ils soient répétés respectivement en haut et en bas dans un même monôme.
Quand le symbole prime est utilisé pour distinguer deux bases distinctes d'un même espace vectoriel, on peut encore simplifier la notation en plaçant le symbole prime sur l'indice plutôt que sur le vecteur : x = x'^k e'k = x^k' ek'
Certains termes d'une somme peuvent comporter plusieurs indices. Par exemple, dans la somme a^km b^m, la sommation se fait sur l'indice m. L'indice k (appelé indice libre) caractérise alors un terme particulier.
Ainsi, l'équation ck = a^km b^m pour n = 3 représente le système d'équations :
c1 = a¹1 b¹ + a¹2 b² + a¹3 b³
c2 = a²1 b¹ + a²2 b² + a²3 b³
c3 = a³1 b¹ + a³2 b² + a³3 b³
Il n'y a pas ici de sommation sur l'indice k, celui-ci se trouvant seul dans le même monôme.
Lorsque le monôme comporte plusieurs indices muets, la sommation se fait à la fois sur tous ces indices. Par exemple, a^km b^m ck pour n = 4 représente une somme de 16 termes :
a^km b^m ck = a¹1 b¹ c1 + a¹2 b² c1 + a¹3 b³ c1 + a¹4 b⁴ c1 + ... + a²1 b¹ c2 + ... + a⁴4 b⁴ c4

La convention de sommation s'applique également aux Dérivées partielles (exemple : g^il,l) et aux Dérivées covariantes (exemple : F^kl_;l), bien que le symbole de dérivée ne soit pas un indice covariant [DENIS, Cours, p.25].
Pour la Dérivée covariante, la contraction de l'indice d'un tenseur par l'indice de dérivation est en effet légitime en raison de la nature tensorielle de la Dérivée covariante et de la propriété de linéarité des tenseurs.

Courbure

Le mot "courbure" a plusieurs significations en Relativité :

Les trois premières courbures dépendent uniquement des potentiels de gravitation gab et de leurs dérivées premières et secondes par rapport aux coordonnées. En Métrique de Minkowski, elles sont toutes nulles et correspondent à l'Espace-temps plat de la Relativité Restreinte.

Courbure scalaire (ou invariant scalaire)

La courbure scalaire de l'Espace-temps est un nombre (R) de dimension m^-2 obtenu par Contraction du Tenseur de Ricci sous la forme :

R est en fait la trace du tenseur de Ricci.

Covariance d'une loi physique (ou principe de Relativité Générale)

La covariance générale d'une loi physique n'a rien à voir avec la Covariance des composantes d'un tenseur. Le mot "covariance" ne se réfère pas à l'indice covariant d'un Tenseur mais indique seulement une écriture de la loi physique qui reste invariante de forme sous une transformation quelconque des coordonnées (invariance par difféomorphisme) [AMI Initiation_aux_Tenseurs, p.18].
Lorsque la loi physique peut s'écrire sous la forme tensorielle : T = 0, ou ce qui revient au même : P = Q avec T = P - Q (T, P et Q étant des Tenseurs de même type), alors tout changement de référentiel transforme cette équation sous la forme tensorielle : T' = 0, ce qui ne change pas la forme de la loi physique.

Exemple de la loi de Newton : F = m γ
L'expression covariante de cette loi est en composantes contravariantes [AMI Initiation_aux_Tenseurs, p.18] :
    Fⁱ = m vⁱ_;t
avec : vⁱ = dxⁱ/dt
Le terme vⁱ_;t est la Dérivée covariante de la vitesse vⁱ par rapport au temps t, laquelle vaut :
    vⁱ_;t = vⁱ_;k (dx^k/dt) = vⁱ_,k (dx^k/dt) + Γⁱjk v^j v^k = dvⁱ/dt + Γⁱjk v^j v^k
où Γⁱjk sont les Symboles de Christoffel.
Si, de plus, la force F dérive d'un potentiel sous la forme : F = -grad(Φ), alors F peut s'écrire en composantes contravariantes : Fⁱ = g^ij Fj = - g^ij dΦ/dx^j
où les g^ij sont les composantes inverses du Tenseur métrique.
La loi de Newton s'écrit alors sous forme tensorielle :

Sous cette forme tensorielle, la loi de Newton restera invariante de forme sous une transformation quelconque des coordonnées (coordonnées sphériques par exemple).

Autre exemple : les Equations de Maxwell.

Covariance et contravariance

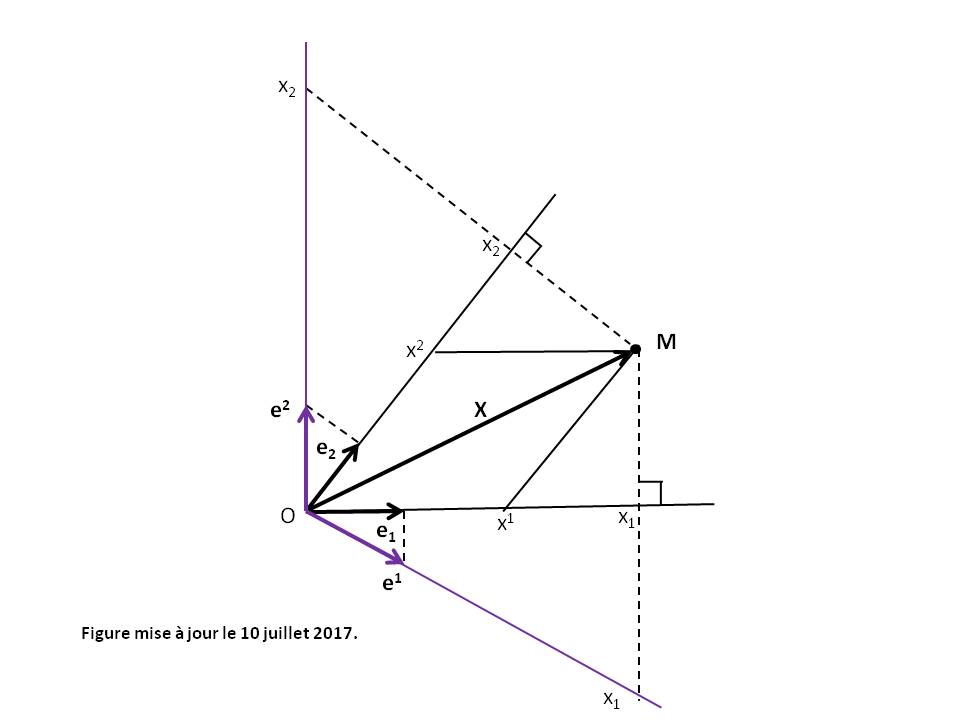
Les notions de vecteur covariant et contravariant s'appliquent à des référentiels non orthonormés, ce qui explique qu'elles ne sont pas abordées dans les cours de mathématiques du Secondaire voire du Supérieur. Lorsque la base est Orthonormée, il n'y a pas de différence entre composantes covariantes et contravariantes.
Pour un espace vectoriel E de dimension n ayant pour vecteurs de base l'ensemble (e1, e2... en), on appelle (voir Figure ci-dessus) :

Les composantes contravariantes sont notées avec des indices supérieurs.
Les composantes covariantes sont notées avec des indices inférieurs.
L'appellation contravariante (resp. covariante) vient du fait que ces composantes se transforment, lors d'un changement de base, de manière inverse (resp. identique) à celle des vecteurs de base.
Lorsque les indices varient de 0 à 3, on emploie souvent les lettres grecques (telles que α ou μ) plutôt que les lettres latines (telles que i ou j).
On a les relations suivantes :

où les coefficients gij sont les composantes du Tenseur métrique.

Dérivée covariante (ou gradient)

La dérivée covariante est l'expression générale de la dérivée qui reste invariante de forme sous une transformation quelconque des coordonnées. Elle contribue à rendre Covariantes les lois physiques.
Selon la procédure générale énoncée par Einstein [BARRAU, Relativité générale, p.64], "on obtient les lois physiques correctes en remplaçant les dérivées usuelles par des dérivées covariantes".

En utilisant la Convention de dérivée partielle et la Convention de sommation, pour tout Tenseur U d'ordre (n), sa dérivée covariante est le tenseur d'ordre (n + 1) de composantes suivantes (notées U _;l ou D_l U) :

où Γⁱjk sont les Symboles de Christoffel.

Dérivée partielle (convention)

Voir Convention de dérivée partielle.

Dilatation des durées (ou Ralentissement des horloges mobiles)

Voir explication simple dans Relativité du temps, définition simple dans Temps, définition rigoureuse dans Facteur de Lorentz et application pratique dans GPS.

Dilatation du temps gravitationnel

La dilatation du temps gravitationnel est un phénomème de relativité générale qui stipule que le temps s'écoule plus lentement en présence d'un champ gravitationnel.
Ainsi, une horloge située loin d'une masse importante (comme une planète ou une étoile) indiquera un temps plus long par rapport à une horloge située près d'une masse importante (dans un champ gravitationnel plus fort).
Ce phénomème a été prédit en 1915 par Albert Einstein.
J.C. Hafele & R.E. Keating ont réalisé en 1971 une expérience qui a consisté à embarquer quatre horloges atomiques au césium sur des avions de ligne pour un tour du monde (avec escales) et à comparer au retour le temps mesuré par ces horloges avec des horloges identiques restées au sol.
Il s'agit d'une réalisation du fameux paradoxe des jumeaux bis.
L'expérience a pleinement confirmé l'Effet Einstein de dilatation du temps gravitationnel (relativité générale) ainsi que la dilatation des durées pour les corps en mouvement (relativité restreinte) [GOU, Relativité Générale, pp 222, 269].

Divergence

La divergence d'un champ de vecteurs rend compte de la variation infinitésimale du volume (ou de la charge électrique) autour d'un point. La divergence d'un Tenseur généralise cette notion.
La divergence d'un tenseur U d'ordre (n) est le tenseur Div(U) d'ordre (n - 1) obtenu en Contractant un des indices de la Dérivée covariante avec l'indice de dérivation.
Pour un tenseur deux fois contravariant, il y a deux divergences possibles : divergence à droite (composante U^ij _;j) et divergence à gauche (composante U^ij _;i). Les divergences ne sont égales que si le tenseur est Symétrique ou Antisymétrique.

Exemple : Le Tenseur d'Einstein modifié Sab est à divergence nulle (Sab_;a = 0).

Propriétés :
Soit deux tenseurs U et V de même ordre. L'opérateur Div() étant linéaire, on a :
- Additivité : Div(U + V) = Div(U) + Div(V)
- Multiplication par un scalaire s : Div(s U) = s Div(U) + U.grad(s), le second terme ayant pour composantes : (U.grad(s))i...k = Ui...kl d(s)/d(x^l)

Dual (espace et base)

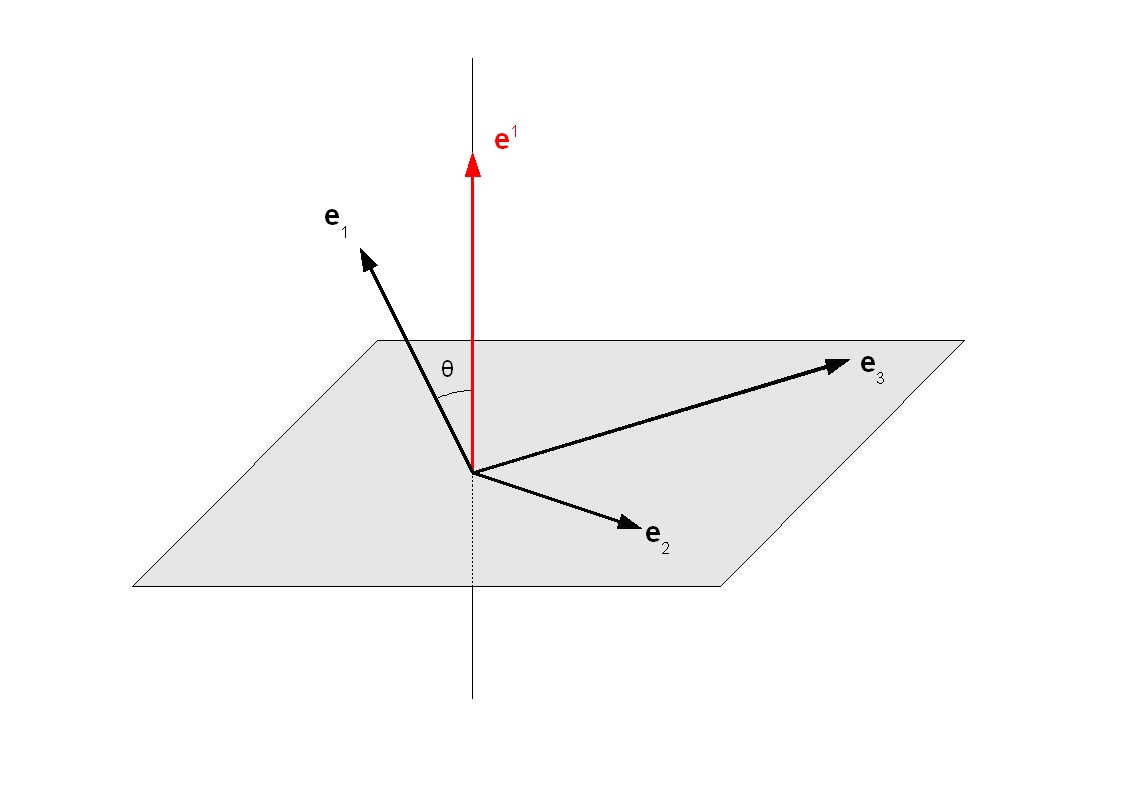
L'espace dual E* d'un espace vectoriel E est l'espace des Formes linéaires coordonnées sur E.
E* est également un espace vectoriel et de même dimension (n) que E.
Si ej sont les vecteurs de base de E et eⁱ les vecteurs de base de E*, alors on a les relations suivantes :

où δ est le Symbole de Kronecker

Tout vecteur x s'exprime donc dans chaque base comme suit :
    x = xi eⁱ
    x = xⁱ ei
où xi et xⁱ sont respectivement les composantes Covariantes et contravariantes du vecteur x.

Interprétation géométrique (voir Figure ci-dessus) :
Le vecteur eⁱ est orthogonal (par rapport au Produit scalaire) à tous les vecteurs ej d'indice j différent (eⁱ.ej = 0) et possède un produit scalaire égal à 1 avec le vecteur ej de même indice (eⁱ.ei = 1).

Propriétés :
ei = gij e^j
eⁱ = g^ij ej
où gij et g^ij sont respectivement les composantes directes et inverses du Tenseur métrique

Effet Doppler (ou Doppler-Fizeau)

L'effet Doppler est le changement de fréquence d'un phénomène périodique induit par le mouvement de l'émetteur par rapport au récepteur. Dans le cas des ondes sonores par exemple, le son émis par une voiture qui s'approche est plus aigu que celui émis lorsqu'elle s'éloigne.
Prenons le cas général en Relativité Restreinte d'une onde lumineuse se propageant à la vitesse d'onde c.
Si f est la fréquence de l'onde perçue par un Observateur O d'un référentiel R, alors tout Observateur O' d'un référentiel R' en translation rectiligne uniforme de vitesse v par rapport à R percevra cette même onde à une fréquence f' différente de f. L'expression de f' est la suivante selon différents cas.
u est le vecteur unitaire de la propagation lumineuse MO (voir Figure dans Aberration).
γ est le Facteur de Lorentz

(D1) Effet Doppler longitudinal (u parallèle à v) :
    f' = f γ (1 - (v.u)/c)
Lorsque v est petit devant c, on retrouve les formules approximatives non relativistes :
    f' = f (1 - (vr.u)/c) pour des récepteur mobile (vitesse vr = v) et émetteur immobile par rapport au milieu de la propagation
    f' = f / (1 - (ve.u)/c) pour des récepteur immobile et émetteur mobile (vitesse ve = -v) par rapport au milieu de la propagation
    f' = f (1 - (vr.u)/c) / (1 - (ve.u)/c) pour des récepteur mobile (vitesse vr) et émetteur mobile (vitesse ve) par rapport au milieu de la propagation (vitesse relative vr - ve = v).

(D2) Effet Doppler transversal à l'émission (u perpendiculaire à v dans R) :
    f' = f γ

(D3) Effet Doppler transversal à la réception (u perpendiculaire à v dans R') :
    f' = f γ^-1

(D4) Effet Doppler (formule générale) :
Si la propagation u de la lumière fait avec la vitesse v un angle θ dans R ou θ' dans R' (voir Figure dans Aberration), alors on a la relation :

la relation entre les angles θ et θ' étant donnée par la formule d'Aberration.
Pour θ = θ' = 0° ou 180°, on retrouve la formule (D1) avec décalage vers le rouge ou vers le bleu selon que l'Observateur de R' s'éloigne ou se rapproche de la source lumineuse de R.
Pour θ = 90°, on retrouve la formule (D2) avec décalage vers le bleu.
Pour θ' = 90°, on retrouve la formule (D3) avec décalage vers le rouge.
Lorsque v est petit devant c, on retrouve la formule approximative non relativiste :
    f' = f (1 - (vr.u)/c) / (1 - (ve.u)/c) pour des récepteur mobile (vitesse vr) et émetteur mobile (vitesse ve) par rapport au milieu de la propagation (vitesse relative vr - ve = v).

Effet Einstein (ou décalage spectral gravitationnel ou effet Doppler gravitationnel)

La fréquence d'une source lumineuse produite dans un champ de gravitation est diminuée (donc décalée vers le rouge) quand elle est observée depuis un lieu où la gravitation est moindre. Il s'agit d'un pur effet de Relativité Générale et non d'un décalage par Effet Doppler.
Ce phénomène, prédit en 1915 par Albert Einstein, a été observé en 1960 par Pound & Rebka.
En utilisant la Métrique de Schwarzschild centrée sur un corps massif (masse M) à symétrie sphérique, et dans le cas particulier d'une Constante cosmologique nulle et d'un champ de gravitation dans le vide, la fréquence observée f' à la distance radiale r' est fonction de la fréquence produite f à la distance radiale r selon la loi :

où r^* est le rayon gravitationnel (r^* = 2 G M c^-2).
Lorsque l'Observateur est situé en un lieu de gravitation moindre que le lieu de la source (r' > r), on trouve (f' < f) correspondant à l'observation d'un décalage vers le rouge.

L'effet Einstein a un impact dans la vie quotidienne : si on n'en tenait pas compte dans le champ gravitationnel de la Terre, le système de positionnement GPS serait complètement inopérant !

Effet Shapiro (ou retard de la lumière)

L'effet Shapiro se manifeste par un retard de tout signal électromagnétique (dont la lumière) à proximité d'un champ gravitationnel, par rapport au temps de propagation que ce signal aurait dans un espace-temps plat.
Ce phénomène a été prédit en 1964 par Irwin Shapiro et détecté en 1966 et 1967 par l'antenne radar Haystack du MIT (Massachussets Institute of Technology).

Elévation d'indice

Un indice inférieur peut être changé en un indice supérieur par multiplication avec le Tenseur métrique inverse g^ij puis Contraction des indices. Exemples :
Uⁱk = g^ij Ujk
U^ik = g^il g^km Ulm
Attention : Si on garde la même lettre pour le tenseur résultat (après suppression des indices identiques), alors la notation peut devenir ambigüe (voir Contraction des indices).

Energie et impulsion d'une particule mesurés par un observateur

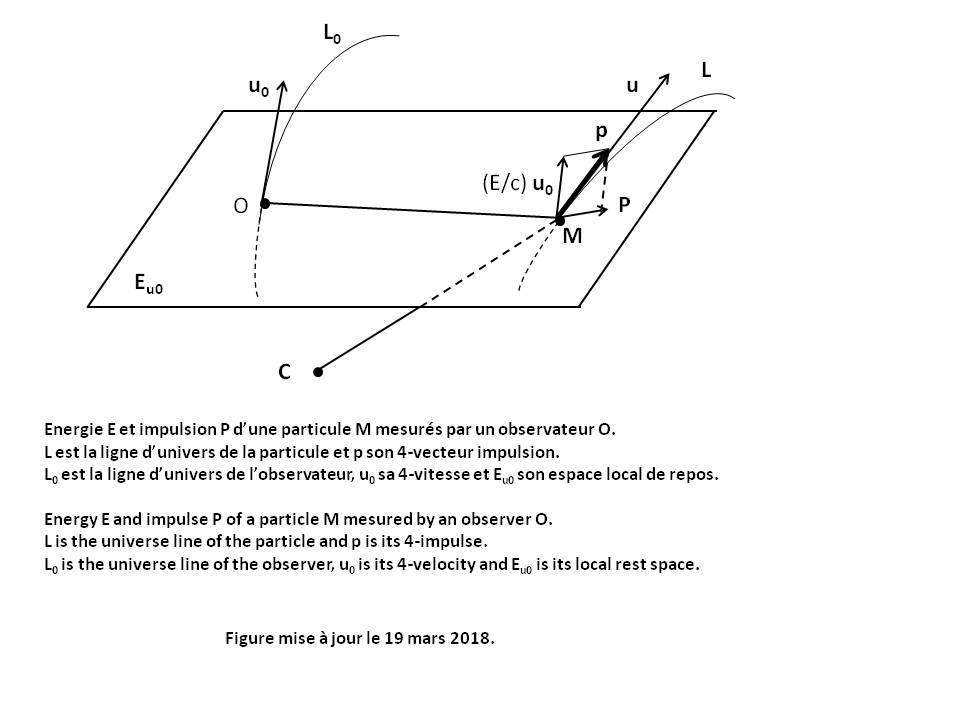
L'énergie E et le vecteur impulsion P d'une particule M, mesurés par un Observateur O dans son Référentiel local à un instant τ, sont donnés par les relations suivantes (voir Figure ci-dessus) [GOU, Relativité Restreinte, p.275 à 278] :

L, p et m sont les Ligne d'univers, Quadri-impulsion et masse au repos (masse propre) de la particule
L0, u0 et a0 sont les Ligne d'univers, Quadri-vitesse et Quadri-accélération de l'Observateur.
γ est le Facteur de Lorentz
ω est la Quadri-rotation de l'Observateur O.
v est la vitesse du point M relative à l'Observateur O dans son Espace local de repos E_u0.
"x_u0" est l'opérateur Produit vectoriel entre deux vecteurs quelconques de E_u0, ce qui s'écrit : ω x_u0 OM = Ε(u0, ω, OM, .)
où :
Ε est le Tenseur de Levi-Civita
Ε(u0, ω, OM, .) désigne le vecteur qui représente la Forme linéaire Ε(u0, ω, OM, z) pour le Produit scalaire g.

Le vecteur impulsion P (de dimension kg.m.s^-1) est la projection orthogonale du vecteur p sur E_u0 (avec P.u0 = 0).
L'énergie E (de dimension J ou kg.m².s^-2) vérifie la relation d'Einstein : E² = m² c⁴ + P.P c² qui se simplifie en : E = ||P|| c pour une particule de masse nulle (cas du photon par exemple).

Lorsque L croise L0 au temps propre τ0 (OM = 0) ou lorsque O est un Observateur inertiel (a0 = ω = 0), ces relations se simplifient en :

La première relation exprime l'équivalence entre masse et énergie. Elle a été établie en 1905 par Einstein [EIN Ist die Trägheit], quelques mois après son article fondateur sur le Relativité Restreinte.
Cette relation peut s'écrire : E = E_mass + E_cin, où E_mass est l'énergie de masse (E_mass = m c²) et E_cin l'énergie cinétique de la particule (E_cin = (γ - 1) m c²).
En limite non relativiste (||v|| << c) avec développement limité de γ, on retrouve que : E_cin = (1/2) m v.v et que : P = m v

L'équivalence masse-énergie a été confirmée indirectement dans les années 1930-1940 par de nombreuses expériences en physique nucléaire et des particules, puis confirmée en 2008 par l'équipe internationale du Centre de Physique Théorique de Marseille en montrant que la masse du proton provient de l'énergie des quarks et des gluons.

Equation d'Einstein (ou Equation de la gravitation relativiste)

Voir L'équation d'Einstein

Equation de Poisson

L'équation de Poisson a été établie par le mathématicien et physicien français Siméon Denis Poisson.
En gravitation universelle Newtonienne, le potentiel gravitationnel (non relativiste) ψ est relié à la masse volumique ρ par l'équation de Poisson :

où Δ est l'opérateur Laplacien (voir Convention de dérivée partielle).
et G est la constante de gravitation universelle (G = 6,6726 10^-11 kg^-1.m³.s^-2).
ψ est de dimension m².s^-2

Equations de Friedmann

Voir Résolution de l'équation d'Einstein avec la Métrique de Friedmann-Lemaître-Robertson-Walker

Equations de Maxwell

Electromagnétisme non relativiste :

Toute particule de charge q et de vitesse v, soumise à un champ électrique E et à un champ magnétique B, subit la force de Lorentz F_LORENTZ = q (E + v x B)

Les équations de James Clerk Maxwell précisent alors l'évolution des champs électromagnétiques E et B. Dans le vide en présence de sources (charges électriques ponctuelles et/ou leurs courants électriques), ces champs s'écrivent :

Les deux densités ρ et J sont reliées par la relation de la conservation des charges (voir démonstration ci-dessous) :
    (R5) div(J) + dρ/dt = 0

E est le champ électrique (en m^-1.V ou C^-1.N ou kg.m.s^-3.A^-1)
B est le champ magnétique (en T ou kg.s^-2.A^-1)
J est la Densité de courant électrique (en m^-2.A)
v est la vitesse de la particule (en m.s^-1)
q est la charge électrique (en C ou s.A)
ρ est la Densité de charge électrique (en m^-3.s.A)
μ₀ est la perméabilité du vide : μ₀ = 4 π 10^-7 kg.m.A^-2.s^-2
ε₀ est la permittivité diélectrique dans le vide telle que :
(R0) ε₀ = 1 / (μ₀ c²)
c est la vitesse de la lumière dans le vide (c = 2,99792458 10⁸ m.s^-1)
Les opérateurs utilisés sont les suivants :
    v1.v2 et v1 x v2 : Produit scalaire et Produit vectoriel de deux vecteurs quelconques v1 et v2.
    div(v) et rot(v) : divergence et rotationnel du vecteur quelconque v (voir Convention de dérivée partielle).
    Δ : opérateur Laplacien (voir Convention de dérivée partielle).
    ◊ : opérateur d'Alembertien (voir Convention de dérivée partielle).

Electromagnétisme relativiste :

Potentiels électrique et magnétique :
A partir des relations (R2) et (R3), on définit le Potentiel électrique V et le Potentiel magnétique A par les relations suivantes (voir démonstration ci-dessous) :
    (R6) rot(A) = B
    (R7) -grad(V) = E + d/dt(A)
Si A vérifie la relation (R6), alors tout potentiel A' = A + grad(Ψ) vérifie également (R6). Le potentiel magnétique A est donc déterminé au gradient d'un champ scalaire Ψ près.
De même, si deux potentiels électriques V et V' vérifient la relation (R7), alors on peut écrire :
-grad(V' - V) = d/dt(A' - A)
On en déduit :
grad(V' - V + d/dt(Ψ)) = 0
V' = V - d/dt(Ψ) + f(t)
Le potentiel électrique V est donc déterminé à une fonction du temps f(t) près.

Condition de jauge de Lorenz :
En reportant les relations (R6) et (R7) dans les relations (R1) et (R4), on trouve :
(Δ - c^-2 d²/dt²)(V) = -ρ/ε₀ - d/dt(C)
(Δ - c^-2 d²/dt²)(A) = -μ₀ J + grad(C)
C = div(A) + c^-2 d/dt(V)
Le potentiel A étant déterminé au gradient d'un champ scalaire Ψ près, on peut poser arbitrairement :
    (R8) C = 0
Cette relation est appelée condition de jauge de Lorenz (du physicien danois Ludvig Valentin Lorenz, à ne pas confondre avec le physicien hollandais Hendrik A. Lorentz), ce qui donne finalement :
    (R9) ◊(V) = -ρ/ε₀
    (R10) ◊(A) = -μ₀ J
Les trois relations (R8), (R9) et (R10) constituent un groupe d'équations qui contiennent les mêmes informations que les équations de Maxwell.
Ces relations sont invariantes par Transformation de Lorentz-Poincaré (voir démonstration ci-dessous). Il en est donc de même pour les équations de Maxwell.

Résolution des équations :
Dans le vide et sans aucune source (ρ = 0 et J = 0), les relations (R9) et (R10) montrent que le champ électromagnétique obéit à deux équations de d'Alembert appelées équations d'onde.
Dans le cas général d'une distribution de sources P localisée dans un domaine D porteur de charges et de courants électriques, ou dont la densité décroît suffisamment rapidement avec la distance, les solutions des équations (R9) et (R10), avec les conditions supplémentaires V(∞) = 0 et A(∞) = 0, sont les suivantes :
    (R11) V(M, t) = ∑_D[ (1/ε₀) (4 π/||PM||) ρ(P, t - ||PM||/c) dτ ]
    (R12) A(M, t) = ∑_D[ μ₀ (4 π/||PM||) J(P, t - ||PM||/c) dτ ]
Ces solutions sont appelées potentiels retardés car les valeurs des potentiels en un point M à un instant t dépendent de celles des sources en tous les points P à l'instant antérieur (t - ||PM||/c).

Démonstrations :

Espace-temps

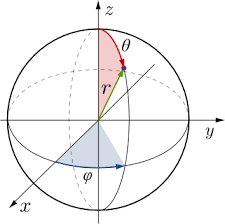
L'espace-temps est un espace à quatre dimensions où le temps n'est plus une grandeur séparée, indépendante de l'espace, mais une variable jouant le même rôle que les variables spatiales. La notion de Simultanéité n'est plus universelle.

Définition [GOU, Relativité Restreinte, p.24] :
L'espace-temps (appelé espace-temps de Minkowski) est défini par l'ensemble des quatre objets mathématiques suivants :
- Espace affine réel de dimension 4, associé à un espace vectoriel E orienté (selon que la base est directe ou indirecte)
- Produit scalaire de Signature (-, +, +, +), associé au Tenseur métrique g
- Cône de lumière avec ses deux flèches du temps (nappe du passé et nappe du futur)
- Tenseur de Levi-Civita Ε associé à la métrique g

Quadri-vecteur et coordonnées :
Dans cet espace-temps d'origine O fixée, un point ou événement x(x, y, z, t) est repéré par un vecteur x à quatre dimensions appelé quadri-vecteur ou 4-vecteur dont les composantes sont notées :

Les coordonnées sphériques sont définies à partir des coordonnées cartésiennes selon les relations suivantes (voir Figure ci-dessus) [GOU, Relativité Générale, p.20] :

D'un point de vue géométrique, r donne l'aire (A = 4 π r²) des sphères d'invariance liées à la symétrie sphérique (sphères avec t = constante et r = constante). La coordonnée r est parfois appelée rayon aréolaire [GOU, Relativité Générale, p.59].

Sens physique :
Les coordonnées ct, x, y, z, r, θ et φ n'ont pas de sens physique (mesurable directement) [GOU, Relativité Générale, p.59] [GOU, Relativité Restreinte, p.430] [EIS Lumière, p.7]. Elles ne sont qu'un moyen formel d'étiqueter les points de l'espace-temps.
Seules les conclusions, accessibles par l'élimination des coordonnées, peuvent prétendre à une signification objective.
Seul le Temps propre a un sens physique en Relativité Restreinte et Générale, et les distances se mesurent en temps propre sur des trajectoires Géodésiques [EIS Lumière, pp 7-8].

Espace-temps plat :
L'espace-temps n'est plat (Tenseur de courbure identiquement nul) que s'il s'agit de l'espace-temps de Minkowski [GOU, Relativité générale, p.200].

Espace local de repos de l'observateur

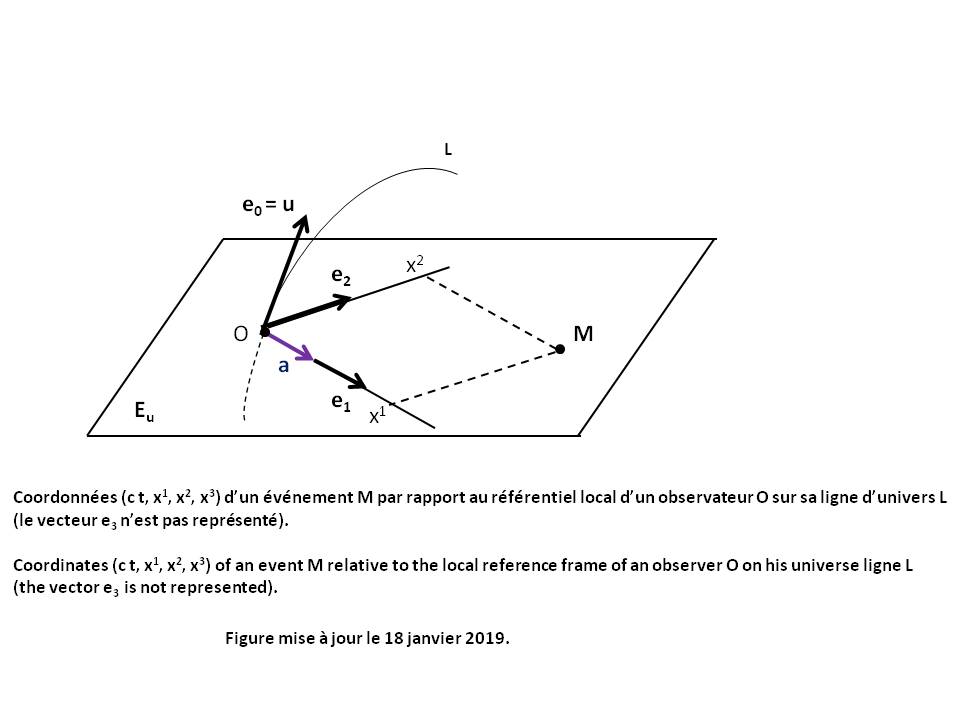
Soit un Observateur O de Ligne d'univers L et de Quadri-vitesse u (voir Figure ci-dessus).
Son espace local de repos est l'hyperplan vectoriel E_u orthogonal à u.

Facteur de Lorentz

Soit un Observateur O de Ligne d'univers L0 et de Quadri-vitesse u0 (voir Figure ci-dessus).
Soit une particule M de Ligne d'univers L et de Quadri-vitesse u.
On suppose que L est située au voisinage de L0, au sens où L peut être décrite dans le Référentiel local de O, ce qui signifie que la distance spatiale entre L0 et L est toujours bien inférieure à ||a0||^-1, où a0 est la Quadri-accélération de O.
Soit un incrément infinitésimal dτ0 du Temps propre τ0 de O et dτ le Temps propre de la particule écoulé lorsqu'elle passe de M(τ0) à M(τ0 + dτ0) le long de sa ligne d'univers.
Le Facteur de Lorentz γ de la particule M par rapport à l'Observateur O est défini par la relation suivante [GOU, Relativité Restreinte, p.99 à 109] :

On démontre alors les relations suivantes :

ω est la Quadri-rotation de l'Observateur O.
v est la vitesse du point M relative à l'Observateur O dans son Espace local de repos E_u0.
"x_u0" est l'opérateur Produit vectoriel entre deux vecteurs quelconques de E_u0, ce qui s'écrit : ω x_u0 OM = Ε(u0, ω, OM, .)
où :
Ε est le Tenseur de Levi-Civita
Ε(u0, ω, OM, .) désigne le vecteur qui représente la Forme linéaire Ε(u0, ω, OM, z) pour le Produit scalaire g.

Lorsque L croise L0 au temps propre τ0 (OM = 0) ou lorsque O est un Observateur inertiel (a0 = ω = 0), ces relations se simplifient en :

Lorsque L croise L0 au temps propre τ0 (OM = 0) ou lorsque la Quadri-accélération a0 de O est nulle (en particulier si O est un Observateur inertiel (a0 = ω = 0)), alors on démontre que : γ ≥ 1. Etant donné la définition de γ comme rapport de deux durées propres, cette propriété est appelée Dilatation des durées.

Forme linéaire

Figures ci-dessus de gauche à droite : René Maurice Fréchet et Frigyes Riesz

Toute forme linéaire ω est une application qui, à tout vecteur u, fait correspondre un nombre ω(u), et ceci de manière linéaire [GOU, Relativité Restreinte, p.21] :

ω(u) est parfois noté <ω, u> avec la notation bra-ket comme en mécanique quantique.

Exemples : si a et b sont des vecteurs d'un espace vectoriel E, les applications linéaires qui, au vecteur u, font correspondre respectivement les scalaires u.a et det(u, a, b) sont toutes deux des formes linéaires.

Propriétés :
- Il existe un unique vecteur w qui représente la Forme linéaire ω de l'espace Dual (E*) pour le Produit scalaire.
- Le vecteur w vérifie la relation : w.z = ω(z) pour tout vecteur z
- Dans toute base {ei} de E, ses composantes Covariantes s'écrivent : wi = w.ei = ω(ei) et ses composantes contravariantes s'écrivent : wⁱ = g^ij wj = g^ij ω(ej) = ω(g^ij ej) = ω(eⁱ)
- Notation [GOU, Relativité Restreinte, p.87, 538] : Le vecteur w se note parfois : w = ω(.)

Genre d'un vecteur

Un vecteur quelconque v de l'Espace-temps est dit :
- du Genre temps lorsque le Produit scalaire v.v < 0. C'est le cas du vecteur tangent à la trajectoire d'une particule de masse non nulle. Deux événements de l'Espace-temps peuvent être reliés par une information allant à une vitesse inférieure à celle de la lumière.
- du Genre lumière (ou vecteur lumière ou vecteur isotrope) lorsque le Produit scalaire v.v = 0 avec v ≠ 0. C'est le cas du vecteur tangent à la trajectoire d'une particule de masse nulle (photon par exemple). Deux événements de l'Espace-temps peuvent être reliés par une information allant à la vitesse de la lumière.
- du Genre espace lorsque le Produit scalaire v.v > 0. C'est le cas du vecteur ni Genre temps ni Genre lumière. Deux événements de l'Espace-temps ne peuvent pas être reliés par une information allant à la vitesse de la lumière.

Par définition, les vecteurs du Genre temps, lumière et espace sont situés respectivement à l'intérieur, sur la surface et à l'extérieur du Cône de lumière.

Géodésique

Pour une Métrique relativiste donnée, une géodésique est la courbe (ou trajectoire) de plus courte distance entre deux points donnés.
Les géodésiques décrivent donc le mouvement des particules libres (systèmes matériels ou photons), c'est-à-dire lorsqu'elles ne sont pas soumises à une force externe autre que la gravitation dans le cadre de la Relativité Générale.
John Archibald Wheeler, spécialiste américain de la Relativité Générale, dit : "La matière dit à l'espace-temps de se courber et l'espace-temps dit à la matière comment se déplacer".

Si l'on choisit de paramétrer la trajectoire par le Temps propre τ satisfaisant à : ds² = -c² dτ², les équations tensorielles des géodésiques s'écrivent comme suit [GOU, Relativité Générale, p.48] :

Si le Tenseur métrique g est connu (et donc Γ), cette équation constitue un système de 4 équations différentielles du second ordre pour les 4 fonctions xⁱ. D'après le théorème de Cauchy, ce système admet une solution unique si on se fixe les conditions initiales suivantes :
    xⁱ(0) = quatre constantes arbitraires
    (dxⁱ/dτ)(0) = uⁱ₀
    uⁱ₀ étant quatre constantes vérifiant : gij uⁱ₀ u^j₀ = -c²

En Relativité Restreinte (Métrique de Minkowski) avec coordonnées cartésiennes, les coefficients gij sont tous constants, ce qui annule tous les symboles de Christoffel. Les équations des géodésiques se réduisent alors à : d²xⁱ / dτ² = 0 dont les solutions sont les lignes droites ordinaires : xⁱ(τ) = aⁱ(τ) τ + bⁱ

Géodésique d'un corps matériel

Trajectoire :
La trajectoire d'un corps matériel dans un champ gravitationnel à symétrie sphérique (Métrique de Schwarzschild) est une Géodésique de Genre temps [GOU, Relativité Générale, p.71].
On suppose que la masse m du corps matériel est petite devant la masse M du corps central de la métrique de Schwarzschild et que l'Observateur est placé dans le plan équatorial z = 0 du corps central (θ = π/2, voir Figure dans Espace-temps).
La trajectoire du corps matériel est plane et donnée par l'équation différentielle suivante [GOU, Relativité Générale, pp80, 74, 72, 63, 64] :

avec :
r* = rayon de Schwarzschild (r* = 2 G M c^-2)
M = masse du corps central
ε (en m².s^-2) = c² (1 - r*/r) dt/dτ = -c² ut.u = -c² g00 u⁰
l (en m².s^-1) = r² sin²[θ] dφ/dτ = c uφ.u = c g33 u³
l_crit = 3^1/2 r* c
u = Quadri-vitesse du corps matériel
ut et uφ = vecteurs de la Base naturelle associés respectivement à la stationnarité et à la symétrie azimuthale de la métrique
τ = Temps propre du corps matériel.

A noter que les deux quantités ε et l sont constantes le long de la Géodésique.
En Limite Newtonienne (lorsque le corps matériel est infiniment éloigné du corps central), on peut interpréter ε et l comme suit :
    ε = c² + E0/m = énergie par unité de masse du corps matériel, mesurée par un Observateur statique.
    l = moment cinétique (par rapport à l'axe z) par unité de masse du corps matériel, mesuré par un Observateur statique.
    E0 = énergie mécanique du corps matériel (somme de l'énergie cinétique et de l'énergie potentielle gravitationnelle).

Selon les valeurs couplées de l et ε, la trajectoire du corps matériel est alors la suivante [DEV, Un peu de physique, Trajectoire d'une particule] :
Dans le cas où : |l| < l_crit, le corps matériel est attiré irrémédiablement par le corps central.
Dans le cas où : |l| > l_crit, le corps matériel évite le corps central en continuant sa course ou, au contraire, se met en orbite autour.
Dans le cas d'une orbite, la trajectoire peut être un cercle parfait ou une quasi-ellipse avec avance du périastre (voir Figure ci-dessus). A la Limite Newtonienne, la trajectoire est une ellipse stable qui vérifie les lois de Kepler.

Périaste :
Le périastre est le point de la trajectoire la plus proche du corps central (voir Figure ci-dessus).
L'avance δφ_per du périastre (au premier ordre en r*/r) est la suivante [GOU, Relativité Générale, p.82] :

avec :
a = demi-grand axe de l'ellipse
e = excentricité de l'ellipse

Dans le cas de l'avance du périastre autour du Soleil (périhélie) de la planète Mercure (avec M_Soleil = 1,9891 10³⁰ kg, a_Mercure = 5,79 10¹⁰ m, e_Mercure = 0,206), on trouve : δφ_per = 5,0 10^-7rad. La période orbitale de Mercure étant de 88 jours, l'effet cumulé au bout d'un siècle est : Δφ_per = 43"
Cette avance a été observée dès 1859 par Urbain le Verrier et expliquée en 1915 par Albert Einstein [EIN Die_Grundlage].

Géodésique d'un photon

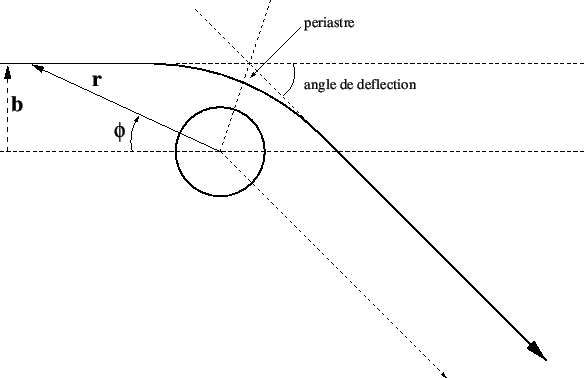
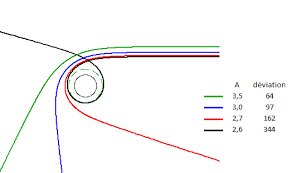
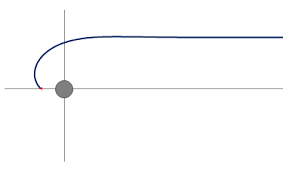
Figures ci-dessus de gauche à droite : Figure 1 = Déviation des rayons lumineux pour b grand ; Figures 2 à 4 issues de [DEV Un peu de Physique - Trajectoire d'un rayon lumineux] = Déviation des rayons lumineux selon la valeur de b

Trajectoire :
La trajectoire d'un photon dans un champ gravitationnel à symétrie sphérique (Métrique de Schwarzschild) est une Géodésique de Genre lumière [GOU, Relativité Générale, p.82].
On suppose que l'Observateur est placé dans le plan équatorial z = 0 du corps central de la métrique (colatitude θ = π/2, voir Figure dans Espace-temps).
La trajectoire du photon est plane et donnée par l'équation différentielle suivante [GOU, Relativité Générale, p.85, 86] :

avec :
r* = rayon de Schwarzschild (r* = 2 G M c^-2)
M = masse du corps central
b = paramètre d'impact pour les photons arrivant depuis l'infini (voir Figure 1 ci-dessus)
b_crit = (3/2) 3^1/2 r*

Dans le cas où : b > b_crit, les photons en provenance de l'infini vont s'approcher du corps central et repartir vers l'infini. La trajectoire ressemble à une hyperbole pour les grandes valeurs de b (voir Figure 1 ci-dessus) et peut faire plusieurs fois le tour du corps central avant de repartir pour les valeurs de b proches de b_crit (voir Figure 2 ci-dessus).
Dans le cas où : b ≤ b_crit, les photons sont piégés par le corps central et un Observateur distant ne pourra pas les recevoir (voir Figures 3 et 4 ci-dessus).

Cette équation différentielle s'intègre sous la forme suivante, qui se résoud sous forme d'une intégrale elliptique [DEV Un peu de physique - Trajectoire d'un rayon lumineux].

Périaste :
Le périastre est le point de la trajectoire la plus proche du corps central (voir Figure 1 ci-dessus).
Son rayon r_per est donné par l'équation suivante [GOU, Relativité Générale, p.86] :

Cette équation du troisième degré se résoud comme suit :

Déviation :
Dans le cas : b >> b_crit et au premier ordre en r*/b, la déviation δφ du rayon lumineux par rapport à un trajet en ligne droite (voir Figure 1 ci-dessus) est alors la suivante [GOU, Relativité Générale, p.86, 87] :

Dans le cas d'une trajectoire rasant la surface du Soleil (b = R_Soleil = 6,96342 10⁸ m, avec M_Soleil = 1,9891 10³⁰ kg), on trouve : r* = 3,0 10³ m et δφ = 1,75"
Cette déviation, prédite en 1915 par Albert Einstein, a été mise en évidence par Arthur Eddington et son équipe, en mesurant la position des étoiles au voisinage du disque solaire lors de l'éclipse de 1919. C'est cet événement qui a rendu Einstein célèbre auprès du grand public.
La déviation des rayons lumineux est à l'origine du phénomène de Mirage gravitationnel.

Rayon apparent :
Pour un Observateur situé à l'infini, le rayon apparent Ra d'une étoile de rayon R et celui d'un Trou noir de rayon r* (considéré comme délimitant sa "surface") valent alors [GOU, Relativité Générale, p.299, 300] :

L'étoile apparaît donc toujours plus grosse qu'elle n'est (Ra > R).
Pour un Trou noir, les photons de faible paramètre d'impact (b < b_crit) sont piégés par le Trou noir et l'Observateur ne reçoit aucun photon. Il observe donc sur le fond du ciel un disque noir de rayon apparent presque trois fois plus gros qu'il n'est (Ra = 2,60 r*).

GPS

Le Système GPS (Global Positionning System), connu initialement sour le nom NAVSTAR (NAVigation System by Timing And Ranging), est un système de positionnement dans les trois dimensions (latitude, longitude, altitude), très précis et à couverture mondiale, mis en service dans les années 1970-1980 par le Département de la Défense des Etats-Unis (DoD).
Le GPS est relatif au système géodésique mondial WGS84 (voir Meteo - Annexe 2).
En 2024, en service standard (gratuit), le GPS fournit une précision de 3 à 5 m en horizontal et de 5 à 8 m en vertical.
L'homologue européen du GPS est le système GALILEO, opérationnel depuis 2016.
GALILEO est relatif au système géodésique européen GTRF qui est compatible avec le WGS84 à moins de 1 m près.
En 2024, en service standard (gratuit), GALILEO fournit une précision de 1 m en horizontal et de 2 m en vertical. Le service de haute précision (HAS), également gratuit, accessible seulement aux récepteurs haut de gamme, fournit une précision de 20 cm en horizontal et de 40 cm en vertical.

Détail du GPS (cf [GOU, Relativité Générale, p. 203-205]) :
Le GPS est basé sur un ensemble d'au moins 24 satellites répartis 4 par 4 sur 6 orbites circulaires de période orbitale T = 12 h et de rayon r_sat = 26561 km = 4.16 R_Terre (avec R_Terre = 6378 km et M_Terre = 5.97 10²⁴ kg). Voir Figure ci-dessus.
Chaque satellite (i) transporte une horloge atomique au césium et émet un signal radio comprenant sa date d'émission (ti) et ses trois coordonnées spatiales ri (déduites des éphémérides liées à son orbite).
Tout Observateur sur Terre qui reçoit au même instant (t) les signaux d'au moins quatre satellites peut alors calculer sa position r. Si l'Espace-temps était plat (Métrique de Minkowski), l'observateur devrait simplement résoudre le système de 4 équations : ||r - ri|| = c (t - ti). Mais dans la réalité, il faut considérer impérativement trois types de décalage temporel :
1. Imprécision des horloges atomiques au césium :
Pour avoir une précision de un mètre sur la position r, il faut une précision sur les dates ti de l'ordre de 3 ns (dt = 1 m / c). La stabilité des horloges atomiques au césium est telle que : dt/t = 10^-13. On atteint ainsi dt = 3 ns en t = 10 h environ. Pour atteindre la précision requise, les horloges sont alors réglées plusieurs fois par jour grâce à des signaux envoyés depuis le sol.
2. Dilatation des durées :
Cette dilatation des durées constitue l'Effet Doppler transverse (du second ordre). L'effet Doppler du premier ordre en v/c n'affecte que la fréquence du signal et non pas le contenu du message délivré (date et position de l'émetteur).
Les satellites étant en mouvement par rapport à l'observateur, leur vitesse orbitale vaut : v = (G M_Terre / r_sat)^1/2 = 3.87 km.s^-1. Il en résulte que : dt/t = γ - 1 = 8.3 10^-11 (γ étant le Facteur de Lorentz). Si aucune correction n'est appliquée, on atteint dt = 3 ns en 30 secondes !
3. Effet Einstein :
Les satellites étant quatre fois plus élevés que l'observateur au sol, l'Effet Einstein s'applique donc avec un décalage : dt/t = G M_Terre c^-2 (1/R_Terre - 1/r_sat) = 5.3 10^-10
Si aucune correction n'est appliquée, on atteint dt = 3 ns en 6 secondes, ce qui correspondrait à une erreur de positionnement de 14 km en un jour !
Pour tenir compte de ces deux décalages relativistes, la fréquence propre des horloges atomiques est corrigée avant l'émission du signal radio vers la Terre (voir [GOU, Relativité Générale, p. 205, 211]).

Histoire de l'univers

L'histoire de l'univers, depuis sa création il y a environ 13 milliards d'années, est résumée ci-dessous.

Sources :
- https://fr.wikipedia.org/wiki/Calendrier_cosmique_de_Carl_Sagan
- http://www.syti.net/EvolutionStory.html
- https://www.lemonde.fr/passeurdesciences/article/2017/05/31/l-histoire-de-l-univers-condensee-en-un-an_6001909_5470970.html
- https://www4.obs-mip.fr/wp-content-omp/uploads/sites/44/2017/04/histoire_temps_univers.pdf
- https://planet-terre.ens-lyon.fr/ressource/chronologie-terre.xml

Image d'un objet en mouvement

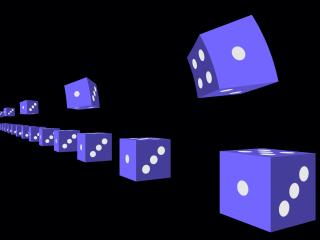
[GOU, Relativité Restreinte, p. 163-171]

- Pour un même Observateur O à un instant fixé τ de son Temps propre, il ne faut pas confondre la position (x, y, z) d'un objet M et son image perçue. Cette image ou photographie est générée par l'ensemble des photons qui arrivent de M en O. En particulier, la Contraction des longueurs concerne la position de l'objet et non son image.
- Pour un cube qui se déplace perpendiculairement à la ligne de visée d'un observateur Inertiel, ce dernier perçoit l'image d'un cube ayant subi une rotation d'un angle θ donné (voir Figure 1 ci-dessus). Il perçoit la face arrière du cube en plus de la face orientée vers lui. Cette rotation apparente n'est pas relativiste et résulte du temps fini de propagation de la lumière. La relativité intervient seulement au travers de la contraction de la face orientée vers l'observateur selon la Transformation de Lorentz-Poincaré.
- L'image d'une sphère en mouvement est une sphère qui paraît avoir subi une rotation et présente sa face opposée au mouvement (voir Figure 2 ci-dessus). Si l'on ne prenait en compte que le temps fini de propagation de la lumière dans une théorie non-relativiste (galiléenne), une sphère apparaîtrait allongée dans la direction du mouvement. C'est grâce à la Contraction des longueurs qu'elle apparaît exactement sphérique. Seule la taille angulaire du cercle peut changer.
- Certains mouvements en astrophysique peuvent être superluminiques, avec une vitesse apparente supérieure à c. Ces vitesses apparentes superluminiques sont engendrées par des mouvements subluminiques dans une direction proche de la ligne de visée. Ainsi le micro-quasar GRS 1915+105 a été observé en 1994 dans notre galaxie avec une vitesse apparente 1.25 c correspondant à une éjection de matière à la vitesse 0.92 c suivant un angle θ de 70°.

Ligne d'univers

La ligne d'univers (ou trajectoire spatio-temporelle) d'une particule matérielle est une courbe de l'Espace-temps (ou chemin séquentiel d'événements) correspondant à l'histoire de la particule.
Par définition, les lignes d'univers des particules matérielles sont toujours situées à l'intérieur du Cône de lumière en un point donné (voir Figure ci-dessus). Ce sont des courbes quelconques de Genre temps. Elles ne sont des Géodésiques que lorsque la particule matérielle n'est soumise à aucune autre interaction que celle induite par le champ gravitationnel.

Limite Newtonienne

L'Equation de Poisson de la gravitation Newtonienne (Δψ = 4 π G ρ) est un cas particulier de l'Equation d'Einstein qui correspond à un espace-temps isotrope spatialement, contenant un fluide parfait non relativiste (p << ρ c²), dans un champ gravitationnel faible (|ψ| << c²), et sans Constante cosmologique (Λ = 0).
Cette limite Newtonienne fournit le coefficient de couplage gravitationnel (K = 8 π G c^-4) utilisé dans l'Equation d'Einstein ainsi que le rayon gravitationnel de Schwarzschild (r^* = 2 G M c^-2) utilisé dans la Résolution de l'équation d'Einstein avec la Métrique de Schwarzschild.

Loi de composition des vitesses

La loi de composition des vitesses en Relativité Restreinte est la suivante :

Soit trois référentiels orthonormés R, R' et R" initialement coïincidents à t = t' = t" = 0, avec leurs axes respectifs parallèles.
R' effectue une translation rectiligne uniforme à vitesse constante v par rapport à R (mesurée dans R), suivi de R" à vitesse constante u par rapport à R' (mesurée dans R'), ces vitesses pouvant être colinéaires ou non.
La vitesse composée w d'un objet immobile dans R" par rapport à R (mesurée dans R) s'écrit alors :

1. Cas où les vitesses u et v sont colinéaires et parallèles à l'axe des x (voir démonstration dans Transformation de Lorentz-Poincaré) :
    (C16) w = (v + u) / (1 + v u / c²)
pouvant s'écrire également :
    (1 - w/c) = (1 - v/c)(1 - u/c)
Cette forme multiplicative montre que la vitesse composée w ne peut jamais dépasser la vitesse de la lumière et que, à des vitesses élevées, la loi de composition n'est plus additive mais multiplicative en termes d'écarts relatifs par rapport à c.

2. Cas où les vitesses u et v sont colinéaires, sans être alignées avec un axe particulier :
La relation (C16) du cas 1 ci-dessus ne contient aucune référence explicite aux coordonnées spatiales x, y et z.
En conséquence, la relation (C16) est indépendante de l'orientation spatiale des vitesses u et v, sous condition d'être colinéaires.
Ce cas se ramène donc au cas n°1 ci-dessus.

3. Cas où les vitesses u et v ne sont pas colinéaires :
L'expression de la vitesse composée w est complexe et dépend de l'ordre d'application des transformations (d'abord v dans le référentiel R, puis u dans le référentiel R').
Par ailleurs, l'expression vectorielle de w peut présenter des différences selon les auteurs, liées à la définition des vitesses u, v et w, ainsi qu'au référentiel de mesure de chacune de ces vitesses. Dans la littérature scientifique, la situation standard est souvent la suivante :
* vitesse v de R' / R, mesurée dans R
* vitesse u de R" / R', mesurée dans R'
* vitesse composée w de R" / R, mesurée dans R
Cette convention permet une application directe et cohérente de la formule de composition des vitesses en Relativité Restreinte, tout en évitant les ambiguïtés potentielles dans l'interprétation des résultats [GOU, Relativité Restreinte, p.142].

Loi de Hubble (ou Loi de Hubble-Lemaître)

L'expansion de l'univers a été prédite en 1922 par Alexander Friedmann.
La loi de Hubble-Lemaître énoncée en 1929 stipule que les galaxies s'éloignent les unes des autres à une vitesse v d'expansion approximativement proportionnelle à leur distance d :

où H(t) est le paramètre de Hubble utilisé notamment dans les Equations de Friedmann.
La vitesse v n'est pas une vitesse physique. Elle traduit seulement la dilatation de l'Espace-temps qui provoque un mouvement d'ensemble des galaxies de l'univers. Ainsi, la Terre "recule devant la lumière" parce que l'Espace-temps se dilate.
La valeur actuelle H(t) (appelée constante H0 de Hubble) vaut environ 70 (km/s)/Mpc, avec 1 pc = 1 parsec = 3,2616 années-lumière = 3,085677581 10¹⁶ m
Toute galaxie lointaine ayant même Temps propre que l'Observateur (appelé Temps cosmique), il n'y a pas d'effet de temps relatif (Effet Doppler-Fizeau) sur sa période de rayonnement mais un simple effet de retard différentiel sur la période du rayonnement reçu.
A ce mouvement d'ensemble se superposent les mouvements propres acquis par les galaxies du fait de leurs interactions gravitationnelles avec leurs voisines.

Mécanique relativiste

La mécanique relativiste se rapporte à la mécanique compatible avec la Relativité Restreinte et la Relativité générale.
Comme en mécanique classique, le sujet peut être divisé en deux : la cinématique qui décrit le mouvement en termes de Quadri-position, Quadri-vitesse, Quadri-rotation et Quadri-accélération, et la dynamique qui décrit la cause du mouvement en termes de Quadri-impulsion, Moment cinétique, Quadri-force et Energie.

Par ailleurs, lorsqu'on passe d'un Observateur à un autre, certaines quantités sont transformées : longueurs et durées (Transformation de Lorentz-Poincaré), vitesses [GOU, Relativité restreinte, p.141], accélérations [GOU, Relativité restreinte, p.151], fréquences (Effet Doppler), angles d'observations (Aberration) et images (Image).

Métrique de Friedmann-Lemaître-Robertson-Walker (ou métrique FLRW)

Figures ci-dessus de gauche à droite : Alexander Alexandrowitsch Friedmann, Georges Lemaître, Howard Percy Robertson et Arthur Geoffrey Walker

La Métrique de Friedmann-Lemaître-Robertson-Walker est une Métrique relativiste correspondant à un espace-temps spatialement homogène et isotrope.
En coordonnées sphériques (r > 0, colatitude θ = [0, π], longitude φ = [0, 2 π]) (voir Figure dans Espace-temps), la métrique s'écrit comme suit, pour tout système de coordonnées (ct, r, θ, φ) et en prenant la convention de Signature (-, +, +, +) :

où k est une constante appelée paramètre de courbure de l'espace qui peut être plate (k = 0), fermée (k = 1) ou ouverte (k = -1) ;
et a(t) une fonction de t uniquement, appelée facteur d'échelle ou facteur de courbure ou rayon de l'univers (a(t) > 0).
La coordonnée r est sans dimension et le rayon (a) a la dimension d'une longueur (en m).
Le cas k = 0 correspond à une platitude des sections spatiales et non de l'Espace-temps.

Les potentiels de gravitation gij sont alors les suivants :

Le signe de d(a)/dt renseigne sur l'évolution de l'univers : positif si expansion, négatif si contraction et nul si statique.
Les coordonnées spatiales (xⁱ) décrivent alors des hypersurfaces spatiales de type espace euclidien (pour k = 0), hypersphérique (pour k = 1) et hyperbolique (pour k = -1), dont la courbure spatiale k* est constante et vaut : k* = 6 k a(t)^-2

Métrique de Minkowski

La Métrique de Hermann Minkowski est une Métrique relativiste correspondant à l'Espace-temps plat de la Relativité Restreinte. Cette métrique est solution de l'Equation d'Einstein sous les conditions Λ = 0 et Tab = 0 (vu que le Tenseur de courbure est nul, donc également le Tenseur de Ricci Rab).

En coordonnées cartésiennes, la mérique s'écrit comme suit, pour tout système de coordonnées (ct, x, y, z) et en prenant la convention de Signature (-, +, +, +) :

Cette métrique gij_MINK a les propriétés suivantes : g^ij = g^ji = gij = gji


En coordonnées sphériques (r > 0, colatitude θ = [0, π], longitude φ = [0, 2 π]) (voir Figure dans Espace-temps), la métrique s'écrit comme suit, pour tout système de coordonnées (ct, r, θ, φ) et en prenant la convention de Signature (-, +, +, +) :

Métrique de Schwarzschild

La métrique de Karl Schwarzschild est une Métrique relativiste correspondant au champ gravitationnel statique et à symétrie centrale. C'est le cas du Soleil et de nombreux astres. Le corps central est à symétrie sphérique et sans être nécessairement statique (par exemple une étoile pulsante qui oscille radialement ou une étoile qui s'effondre en un Trou noir en maintenant sa symétrie sphérique). Le champ gravitationnel doit être par contre statique, même s'il ne l'est pas dans la zone où se trouve la matière. A noter que le champ gravitationnel est nécessairement statique en symétrie sphérique et dans le vide (théorème de Birkhoff).

En coordonnées sphériques (r > 0, colatitude θ = [0, π], longitude φ = [0, 2 π]) (voir Figure dans Espace-temps), la métrique s'écrit comme suit, pour tout système de coordonnées (ct, r, θ, φ) et en prenant la convention de Signature (-, +, +, +) :

où μ et α sont des fonctions uniquement de r.
Les potentiels de gravitation gij sont alors les suivants :

Métrique relativiste

Si (ds) est la distance (ou intervalle) entre deux événements infiniments voisins de l'Espace-temps, alors la métrique relativiste est le "carré" de cette distance et s'écrit :

Dans l'Espace-temps courbe de la Relativité Générale, cette métrique peut être négative, nulle ou positive, et s'écrit en coordonnées cartésiennes :
ds² = g00 (c dt)² + g01 (c dt) dx + g02 (c dt) dy + g03 (c dt) dz +
g10 dx (c dt) + g11 dx² + g12 dx dy + g13 dx dz +
g20 dy (c dt) + g21 dy dx + g22 dy² + g23 dy dz +
g30 dz (c dt) + g31 dz dx + g32 dz dy + g33 dz²
Les coefficients gij sont les composantes du Tenseur métrique.
A noter que la quantité ds² est toujours négative pour une particule matérielle de masse non nulle, le vecteur tangent à sa Ligne d'Univers étant du Genre temps.

Mirage gravitationnel (ou lentille gravitationnelle)

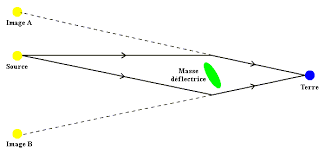
La déviation des rayons lumineux est à l'origine du phénomène de mirage gravitationnel, prédit en 1936 par Albert Einstein et observé en 1979 par Dennis Walsh et ses collègues Robert Carswell et Ray Weymann sur le quasar double QSO 0957+561.
Ce phénomène peut prendre différents aspects en fonction de l'alignement de l'Observateur, de la masse qui déforme (galaxie par exemple) et de la source observée (quasar par exemple). On peut voir des anneaux parfaits (appelés Anneaux d'Einstein), des arcs de cercle ou simplement des images démultipliées de la source (voir Figures ci-dessus).
Non seulement ces lentilles gravitationnelles dévient mais amplifient la lumière déviée, ce qui fascine les astronomes.

Modèle cosmologique standard

Le modèle cosmologique qui décrit le mieux à l'heure actuelle l'Histoire et le comportement de l'univers observable est le modèle standard de la cosmologie (ou modèle avec Big Bang ou modèle Λ-CDM signifiant "Λ Cold Dark Matter").
Ce modèle représente un univers ayant les propriétés suivantes (voir courbe C4 en Figure ci-dessus) :

1. Modèle avec Big Bang (tel que le facteur d'échelle a(t) tende vers 0 quand t tend vers 0).
2. Spatialement homogène et isotrope à grande échelle (donc aussi à courbure spatiale constante). Voir Métrique de Friedmann-Lemaître-Robertson-Walker.
3. Dont la courbure spatiale est nulle (k = 0). A ne pas confondre avec la courbure de l'espace-temps (Tenseur de Ricci) qui mesure la déformation spatio-temporelle de l'univers.
4. Rempli d'un fluide parfait (gaz de galaxies) de densité ρ et d'équation d'état w = p/(ρ c²) qui modélise la matière et l'énergie dans l'univers. Ce fluide est constitué de plusieurs composantes :
    4.1. Matière ordinaire constituée des protons, neutrons et électrons formant les atomes et les molécules. C'est une matière froide, baryonique et non relativiste (w = 0).
    4.2. Matière noire qui est froide, non baryonique et non relativiste (w = 0).
    4.3. Rayonnement et matière chaude incluant toutes les formes de rayonnement électromagnétique (photons) et des particules relativistes comme les neutrinos. Cette composante est chaude et relativiste (w = 1/3).
    4.4. Energie Noire (w = -1) nécessitant : Λ > 0.
5. Conforme au Modèle standard de la physique des particules.

Modèle standard de la physique des particules

Figures : gauche (Voie Lactée avec notre Soleil), milieu (notre Système solaire), droite (Atome).

Le modèle standard de la physique des particules peuplant l'univers est le suivant, avec une description présentée sous forme hiérarchique.

1. Description astronomique
2. Description physique
3. Vocabulaire de base
4. Caractérisation des particules
5. Caractérisation d'une galaxie
6. Caractérisation d'une étoile
7. Caractérisation d'une planète
8. Caractérisation d'un satellite naturel

1. Description astronomique :

Univers observable = Superamas + Filaments galactiques + Vides cosmiques. Taille = environ 93 milliards d'années-lumière.
| Superamas = ensemble d'Amas galactiques. Taille = environ 500 millions d'années-lumière. Exemple : Superamas Laniakea qui inclut l'Amas de la Vierge et le Groupe Local.
|  | Amas galactique = ensemble de Galaxies. Taille = environ 10 millions d'années-lumière. Exemples : Amas de la Vierge qui contient plus d'un millier de Galaxies ; le Groupe Local qui contient environ 50 Galaxies dont la Voie Lactée et Andromède.
|  |  | Galaxie = Etoiles + Systèmes planétaires + Gaz et poussières. Taille = environ 100 000 années-lumière. Exemple : la Voie Lactée qui contient plus de 100 milliards d'Etoiles dont notre Soleil.
|  |  |  | Etoile = corps céleste composé de Gaz en fusion nucléaire . Exemple : notre Soleil.
|  |  |  | Système planétaire = ensemble de planètes, lunes et autres corps en orbite autour d'une Etoile. Taille = environ 0,002 années-lumière soit 20 milliards de km. Exemple : notre Système solaire qui comprend la Terre, Mars, Jupiter, etc.
|  |  |  | Gaz et poussières = constituants diffus dans les Galaxies. Exemple : les nuages de gaz et de poussières contenus dans la nébuleuse d'Orion.
| Filament galactique = filament de Matière noire et de Gaz, canalisant la Matière et l'Energie entre les Superamas et les Amas de Galaxies. Taille = environ 1 milliard d'années-lumière. Exemple : le Grand Mur d'Hercules-Couronne Boréale (Grand Mur HCB).
| Vide cosmique = région quasiment vide de matière. Taille = environ 100 millions d'années-lumière. Exemple : le vide du Bouvier situé dans la constellation du Bouvier, proche du Superamas d'Hercule.

Les mouvements relatifs sont les suivants :
| A l'échelle planétaire : rotation propre des lunes et satellites artificiels + mouvement orbital autour des planètes
| A l'échelle stellaire : rotation propre des planètes et autres corps + mouvement orbital autour des Etoiles
| A l'échelle galactique : rotation propre des Etoiles + mouvement orbital autour du centre galactique + oscillation verticale par rapport au plan galactique (oscillation épicyclique)
| A l'échelle intergalactique : mouvement propre des Galaxies
| A l'échelle cosmologique : expansion de l'univers


2. Description physique :
Nota : les mots isolés (sans commentaire) sont définis dans le Vocabulaire de base.

Univers observable = Matière + Energie
| Matière = Matière ordinaire + Matière non ordinaire
|  | Matière ordinaire (ou baryonique) = Molécules (pouvant exister sous forme de solide, liquide, gaz ou plasma ; exemple l'eau (H₂O)) + Atomes isolés (exemple : Hélium (He)) + Anti-particules
|  |  | Molécule
|  |  | Atome
|  |  | Anti-particules
|  | Matière non ordinaire = Quarks + Leptons non ordinaires + Neutrinos électroniques + Bosons + Anti-particules + Matière noire
|  |  | Quark
|  |  | Lepton non ordinaire
|  |  | Neutrino électronique
|  |  | Boson
|  |  | Anti-particules
|  |  | Matière noire = matière hypothétique produisant un surplus de gravité dont les Galaxies ont besoin pour ne pas se défaire durant leur rotation
| Energie = Rayonnement électromagnétique + Rayonnement cosmique + Energie noire
|  | Rayonnement électromagnétique = énergie transportée par les Photons, classée en fréquence ou longueur d'onde = Rayons gamma + Rayons X + Ultraviolet + Lumière visible + Infrarouge + Micro-ondes + Ondes radio
|  |  | Rayons gamma = très haute énergie produite lors de phénomènes nucléaires et astrophysiques
|  |  | Rayons X = utilisés en imagerie médicale
|  |  | Ultraviolet = responsable des coups de soleil et des réactions chimiques dans la haute atmosphère
|  |  | Lumière visible = ce que l'oeil humain peut voir
|  |  | Infrarouge = chaleur émise par les objets
|  |  | Micro-ondes = utilisées pour chauffer les aliments
|  |  | Ondes radio = faible énergie utilisée pour la communication à longue distance
|  | Rayonnement cosmique = énergie transportée par des particules de haute énergie (souvent des Protons d'Hélium) provenant de sources cosmiques comme les supernovae et les noyaux actifs de Galaxies
|  | Energie noire = énergie hypothétique qui tend à accélérer l'expansion de l'univers


3. Vocabulaire de base :

Molécule = ensemble d'Atomes groupés, tenus par des liaisons chimiques.

Atome = Noyau + Electrons
| Noyau (ou nucléons) = Protons + Neutrons
|  | Proton = particule chargée positivement (spin = 1/2) = deux Quarks "up" et un Quark "down", tenus par la force forte
|  | Neutron = particule non chargée (spin = 1/2) = deux Quarks "down" et un Quark "up", tenus par la force forte
| Electron

Anti-particule = particule de même masse et de même spin que la particule correspondante, mais de nombres quantiques additifs opposés.
Les Anti-particules peuvent-être élémentaires (exemples : Anti-quark, Anti-électron, Anti-muon, Anti-tau, Anti-neutrino, Anti-boson) ou composites (exemples : Anti-proton, Anti-neutron, Anti-noyau, Anti-atome).
Certaines particules, dites "auto-conjuguées", sont leur propre Anti-particule (exemples : Photon, Boson Z, Pion neutre).

Fermions = particules qui constituent la Matière. Elles obéissent au principe d'exclusion de Pauli selon la statistique de Fermi-Dirac et ont un spin semi-entier (1/2, 3/2, 5/2, etc.) ne leur permettant pas d'occuper simultanément le même Etat quantique.
| Fermion composite = tout assemblage de Fermions élémentaires donnant une particule composite de spin semi-entier
| Fermion élémentaire = tout Fermion de type Quark ou Lepton (spin = 1/2)
|  | Quark = plus petite particule du modèle standard de la physique des particules, affecté par la force forte, caractérisée par un spin 1/2 et six "saveurs" : Up, Charm et Top/Thruh (charge = +2/3), Down, Strange et Bottom/Beauty (charge = -1/3).
|  | Lepton = toute particule de spin 1/2, non affectée par la force forte = Electron + Muon + Tau + Neutrino
|  |  | Electron = particule en orbite autour du Noyau, chargé négativement (spin = 1/2). Ne contient pas de Quarks.
|  |  | Muon = particule chargée négativement (spin = 1/2)
|  |  | Tau = particule à durée de vie extrêmement courte, chargée négativement (spin = 1/2)
|  |  | Neutrino = particule de masse extrêmement faible, non chargée (spin = 1/2), caractérisée par trois "saveurs" : électronique, muonique et tauique
|  | Leptons ordinaires = Leptons stables = Electron + Neutrino électronique
|  | Leptons non ordinaires = Leptons instables qui se désintègrent rapidement = Muon + Tau + Neutrino muonique + Neutrino tauique

Bosons = particules qui transmettent les forces fondamentales = Bosons de Jauge + Boson de Higgs. Elles obéissent au principe de superposition selon la statistique de Bose-Einstein et ont un spin entier (0, 1, 2, etc.) leur permettant d'occuper simultanément le même Etat quantique.
| Bosons de jauge = particules médiatrice des forces fondamentales = Photons + Gluons + Bosons W et Z + Gravitons
|  | Photon = particule sans masse, non chargée, spin = 1, médiatrice de la force électromagnétique qui agit sur toutes les particules chargées (Electron, Proton, Ion, Quark, etc.).
|  | Gluon = particule sans masse, non chargée, spin = 1, médiatrice de la force forte qui agit sur les Quarks (cohésion des Hadrons) et sur les Nucléons (cohésion du Noyau).
|  | Bozon W et Z = trois particules massives (W+, W- et Z), chargées pour W+ et W-, non chargées pour Z, spin = 1, médiatrice de la force faible qui agit sur les Quarks et les Leptons, impliquée dans les processus de désintégration radioactive
|  | Graviton = particule hypothétique, non chargée, spin = 2, associée à la gravitation qui agit sur toutes les particules ayant une masse.
| Boson de Higgs = particule non chargée, spin = 0, associée au champ de Higgs qui agit sur les autres Particules élémentaires, leur conférant une forme d'énergie potentielle perçue comme leur masse.

Particules élémentaires = Fermions élémentaires + Bosons + Anti-particules élémentaires

Particules composites = Molécules + Noyaux + Fermions composites + Ions + Hadrons
| Molécule
| Noyau
| Fermion composite
| Ion = Atome ou Molécule modifié électriquement, ayant perdu des Electrons (Cation) ou gagné des Electrons (Anion). Exemples : Ion Sodium (NA⁺) ayant perdu un Electron, Ion Chlorure (Cl^-) ayant gangné un Electron.
| Hadron = toute particule contenant des Quarks, des Anti-quarks et des Gluons = Baryon + Méson + Hadron exotique
|  | Baryon = particule composée de trois Quarks (exemples : Proton, Neutron)
|  | Méson = particule composée d'un Quark et d'un Anti-quark (exemples : Méson pi (Pion), Méson K (Kaon))
|  | Hadron exotique = tout autre combinaison de Quarks et d'Anti-quarks (exemples : tétraquark, pentaquark)

Particules relativistes = particules dont la vitesse est proche de celle de la lumière, donc soumises aux lois de la Relativité = Electrons + Photons + Gluons + Neutrinos

Etat quantique d'une particule :
L'état quantique d'une Particule élémentaire est la description complète de ses propriétés (dynamiques et intrinsèques), incluant sa masse, sa position, son moment cinétique, son spin et ses nombres quantiques associés.
Ces propriétés sont encapsulées dans une fonction d'onde ψ(x, t) ou un vecteur d'état (ψ) permettant de prédire les probabilités des résultats de mesures et illustrant la nature probabiliste de la mécanique quantique.
L'évolution temporelle de la fonction d'onde est gouvernée par l'équation de Schrödinger (pour les Particules non relativistes), de Dirac (pour les Particules relativistes de spin 1/2), de Rarita-Schwinger (pour les Particules relativistes de spin 3/2), de Klein-Gordon (pour les Particules relativistes de spin 0), de Proca (pour les Particules relativistes de spin 1).
Ces équations décrivent le comportement dynamique de la particule de manière déterministe, contrastant avec le caractère probabiliste des mesures individuelles.
Les quatre dernières équations sont invariantes par transformation de Lorentz-Poincaré.
L'état quantique s'applique également aux Particules composites et aux systèmes multi-particulaires, prenant alors en compte les corrélations, interactions internes et phénomèmes d'intrication entre les constituants.


4. Caractérisation des particules :

Les particules sont caractérisées par une liste de propriétés intrinsèques.

Exemple de l'Electron e^- :
| Classification : Lepton
| Composition : N/A (Particule élémentaire)
| Masse (m) = 0,511 MeV/c²
| Nombres quantiques :
|  | Spin (S) = 1/2
|  | Isospin (T₃) = -1/2 (pour l'isospin faible)
|  | Charge électrique (Q) = -1e
|  | Charge de couleur : N/A (particule autre que Quark et Gluon)
|  | Saveur (Le) = électronique
|  | Nombre leptonique (L) = +1
|  | Nombre baryonique (B) = 0
|  | Parité (P) = selon contexte
| Nombres quantiques additionnels (pour l'Electron lié) :
|  | Nombre quantique principal (n) = entier strictement positif
|  | Nombre quantique secondaire ou azimutal (l) = entier de 0 à n
|  | Nombre quantique magnétique (ml) = entier de -l à +l
|  | Nombre quantique de spin (s) = 1/2
|  | Nombre quantique magnétique de spin (ms) = +1/2 ("up") ou -1/2 ("down")
|  | Nombre quantique de moment angulaire total (j) = |l ± s|
|  | Projection du moment angulaire total (mj) = de -j à +j par pas entiers
| Chiralité = Droite et Gauche (mélange possible)
| Symétrie CPT (Charge, Parité, Temps) : Oui
| Polarisation : Oui
| Moment magnétique (μ) = -9,284 10^-24 J/T
| Interactions fondamentales : forces électromagnétique, faible et gravitationnelle
| Durée de vie (τ) = parfaitement stable (6,6 10²⁸ années)
| Anti-particule : positron

Exemple du Positron e⁺ = Anti-électron :
| Classification : Lepton
| Composition : N/A (Particule élémentaire)
| Masse (m) = 0,511 MeV/c²
| Nombres quantiques :
|  | Spin (S) = 1/2
|  | Isospin (T₃) = +1/2 (pour l'isospin faible)
|  | Charge électrique (Q) = +1e
|  | Charge de couleur : N/A (particule autre que Quark et Gluon)
|  | Saveur (Le) = électronique
|  | Nombre leptonique (L) = -1
|  | Nombre baryonique (B) = 0
|  | Parité (P) = selon contexte
| Nombres quantiques additionnels (pour le Positron lié) :
|  | Nombre quantique principal (n) = entier strictement positif
|  | Nombre quantique secondaire ou azimutal (l) = entier de 0 à n
|  | Nombre quantique magnétique (ml) = entier de -l à +l
|  | Nombre quantique de spin (s) = 1/2
|  | Nombre quantique magnétique de spin (ms) = -1/2 ("down") ou +1/2 ("up")
|  | Nombre quantique de moment angulaire total (j) = |l ± s|
|  | Projection du moment angulaire total (mj) = de -j à +j par pas entiers
| Chiralité = Gauche et Droite (mélange possible)
| Symétrie CPT (Charge, Parité, Temps) : Oui
| Polarisation : Oui
| Moment magnétique (μ) = +9,284 10^-24 J/T
| Interactions fondamentales : forces électromagnétique, faible et gravitationnelle
| Durée de vie (τ) = parfaitement stable en isolation et courte en présence de matière
| Anti-particule : électron


5. Caractérisation d'une galaxie :

Une galaxie est caractérisée principalement par la liste de caractéristiques suivante.

Exemple de la Voie Lactée :
| Age = 13 milliards d'années (formée 800 millions d'années après le Big Bang)
| Formation = formation initiale d'un "disque épais", puis collision et fusion, deux milliards d'années plus tard, avec une galaxie naine appelée "Gaia-Encelade".
| Durée de vie = collision prévue dans 4,5 milliards d'années avec la galaxie d'Andromède, avec fusion des deux galaxies pendant deux ou trois milliards d'années supplémentaires.
| Type = galaxie spirale barrée S(B)bc I-II
| Masse = environ 2,0 10¹¹ masses solaires
| Dimensions = disque de diamètre 150 000 années-lumière et d'épaisseur 6 000 années-lumière
| Composition générale (du centre vers la périphérie) = 1. Bulbe central très dense autour du centre galactique, 2.Disque galactique structuré en bras spiraux contenant la majorité des Etoiles, notamment les jeunes Etoiles, 3. Halo galactique contenant des amas globulaires (Etoiles anciennes) ainsi qu'une grande quantité de Matière noire.
| Composition du Bulbe central (du centre vers la périphérie) = 1a. Trou noir super-massif ("Sagittarius A*") situé au coeur de la galaxie, 1b. "Amas Stellaire Nucléaire" composé principalement d'Etoiles anciennes, 1c. "Sagittarius A Ouest", minispirale structurée en filaments de gaz ionisé chaud, 1d. "Sagittarius A Est", vestiges d'une supernova après son explosion, 1e. Disque circo-nucléaire (tore de gaz froid et de poussières).
| Composition du Disque galactique (observée depuis le pôle Nord galactique) = plusieurs bras spiraux dont l'enroulement est antihoraire. L'ordre des bras, de l'extérieur vers l'intérieur de la galaxie, est le suivant (mais sans consensus au niveau scientifique) : 1. Persée, 2. Cygne (ou Aigle), 3. Règle (ou Arc de la Règle ou Norma), 4. Sagittaire (ou Sagittaire-Carène), 5. Centaure (ou Ecu-Croix), 6. Orion (ou Local) dans lequel se situe notre Système solaire.
| Mouvement par rapport au référentiel cosmologique :
|  | Rotation propre = maximale dans le disque galactique (y compris au niveau de notre Soleil) avec une vitesse tangentielle d'environ 250 km/s
|  | Vitesse de déplacement = 600 km/s par rapport au fond cosmologique et 110 km/s en direction de la galaxie d'Andromède (rapprochement)
| Particularités :
|  | Apparence = la Voie Lactée est visible comme une bande laiteuse dans le ciel nocturne, d'oû son nom.


6. Caractérisation d'une étoile :

Une étoile est caractérisée principalement par la liste de caractéristiques suivante.

Exemple de notre Soleil :
| Age = 4,57 milliards d'années
| Formation : Un effondrement gravitationnel d'une région dense d'un immense nuage de gaz et de poussière, appelé "nébuleuse solaire", a provoqué des réactions nucléaires en son centre, marquant ainsi la naissance de notre Soleil.
| Durée de vie : Dans 5 milliards d'années, le Soleil commencera à se transformer en géante rouge, une phase qui durera quelques centaines de millions d'années. Ensuite, le Soleil deviendra une naine blanche, entourée d'une nébuleuse planétaire résultant de l'éjection de ses couches externes.
| Masse = 1,989 10³⁰ kg
| Rayon équatorial = 696 000 km
| Densité moyenne = 1,408 10³ kg/m³
| Composition interne = Hydrogène (73 %) + Hélium (25 %) + métaux (2 %)
| Puissance rayonnée (ou luminosité intrinsèque L) = 3,8 10²⁶ W
| Température de surface = 5500 °C
| Gravité de surface = 274 m/s²
| Position de l'axe de rotation par rapport à la perpendiculaire au plan galactique = 23° à 30° en inclinaison
| Période de rotation propre = entre 25 jours (équateur) et 36 jours (pôles)
| Orbite par rapport au centre galactique (Voie Lactée) :
|  | Distance moyenne au centre galactique = 26 000 années-lumière
|  | Période de révolution = 225 à 250 millions d'années
|  | Position du Soleil par rapport au plan galactique = environ 48 années-lumière au dessus du plan galactique dans le sens du Nord galactique
|  | Inclinaison orbitale par rapport au plan galactique = 7°
|  | Vitesse orbitale moyenne = 220 km/s
| Particularités :
|  | Présence de Système planétaire = Oui (notre système solaire)
|  | Présence de satellites naturels = Non
|  | Présence d'anneaux = Non
|  | Champ magnétique = Oui (5000 μT à la surface, incliné d'environ 10° par rapport à l'axe de rotation)


7. Caractérisation d'une planète :

Une planète est caractérisée principalement par la liste de caractéristiques suivantes.

Exemple de la Terre :
| Age = 4,54 milliards d'années
| Formation : Des collisions entre particules de poussière et de gaz dans le disque protoplanétaire entourant notre jeune Soleil ont progressivement créé des agrégats de plus en plus massifs, menant à la formation de la planète.
| Durée de vie : Dans un milliard d'années, la Terre perdra toute son eau suite à une augmentation de 10 % de la luminosité du Soleil, rendant la vie impossible pour la plupart des formes de vie. Quatre milliards d'années plus tard, elle perdra son atmosphère lorsque le Soleil se transformera en géante rouge, rendant la planète inhospitalière.
| Masse = 5,972 10²⁴ kg
| Rayon équatorial = 6 371 km
| Densité moyenne = 5,515 10³ kg/m³
| Composition interne = noyau interne solide, noyau externe liquide, manteau, croûte
| Composition atmosphérique = 78 % d'azote, 21 % d'oxygène, traces de dioxyde de carbone (0,04 %), vapeur d'eau, argon, etc.
| Pression atmosphérique au niveau de la mer = 101,3 kPa = 1 atm
| Température de surface (à l'ombre) = entre -89°C (station Vostok en Antarctique) et +57°C (Vallée de la Mort en Californie, USA), avec une température moyenne mondiale de 14°C
| Gravité de surface = 9,807 m/s²
| Position de l'axe de rotation par rapport à la perpendiculaire à l'écliptique = 23,44° en inclinaison, et quasiment constante en orientation
| Période de rotation propre (jour sidéral) = 23 h 56 mn 4 s
| Orbite par rapport au Soleil :
|  | Distance moyenne au Soleil (demi-grand axe d) = 149,6 10⁶ km
|  | Périhélie (point le plus proche du Soleil, début janvier) = 147,1 10⁶ km
|  | Aphélie (point le plus éloigné du Soleil, début juillet) = 152,1 10⁶ km
|  | Période de révolution = 365,256 jours
|  | Excentricité de l'orbite = 0,0167
|  | Inclinaison orbitale par rapport au plan de l'ecliptique = 0° par définition
|  | Vitesse orbitale moyenne = 29,78 km/s
|  | Luminosité apparente du Soleil depuis la Terre (ou éclairement E = L / (4 π d²)) = 1360 W/m²
| Particularités :
|  | Position de l'écliptique par rapport au plan galactique (plan principal de la Voie Lactée) = 60° en inclinaison, et selon deux points opposés en intersection
|  | Présence de satellites naturels = Oui (La Lune)
|  | Présence d'anneaux = Non
|  | Champ magnétique = Oui (25 à 65 μT à la surface, incliné d'environ 11° par rapport à l'axe de rotation)
|  | Albédo = variable selon la surface (océans, continents, glace)
|  | Présence de vie = Oui


8. Caractérisation d'un satellite naturel :

Un satellite naturel est caractérisé principalement par la liste de caractéristiques suivante.

Exemple de la Lune :
| Age = 4,51 milliards d'années
| Formation (hypothèse du grand impact) : La Lune se serait formée à partir des débris résultant d'une collision massive entre la jeune Terre et un corps planétaire de la taille de Mars, appelé "Théia"
| Durée de vie : La Lune est désormais considéré comme géologiquement morte. Dans cinq milliards d'années, la transformation du Soleil en géante rouge accentuera son état mort et inhospitalier.
| Masse = 7,347 10²² kg
| Rayon équatorial = 1737 km
| Densité moyenne = 3,34 10³ kg/m³
| Composition interne = noyau, manteau, croûte
| Composition atmosphérique (exosphère) = 25 % de néon, 25 % d'hélium, 23 % d'hydrogène, 20 % d'argon, traces de sodium et d'oxygène
| Pression atmosphérique au niveau de la surface = extrêtrement faible (environ 10^-13 Pa)
| Température de surface = entre -173°C (nuit lunaire) et +127°C (jour lunaire)
| Gravité de surface = 1,62 m/s²
| Position de l'axe de rotation par rapport à la perpendiculaire à son plan orbital = 1,5° en inclinaison, et quasiment constante en orientation
| Période de rotation propre = 27,32 jours
| Orbite par rapport à la Terre :
|  | Distance moyenne à la Terre = 384 400 km
|  | Périgée (point le plus proche de la Terre) = 363 300 km
|  | Apogée (point le plus éloigné de la Terre) = 405 500 km
|  | Période de révolution = 27,32 jours (identique à la période de rotation propre)
|  | Ce phénomène de verrouillage gravitationnel est dû principalement à la différence d'attraction gravitationnelle exercée par la Terre sur les parties de la Lune les plus proches et les plus éloignées, créant un couple de forces tendant à aligner sa rotation propre avec sa révolution orbitale. Ce phénomène se serait produit même si la Terre n'avait pas eu d'océans. Il est indépendant des marées terrestres qui influencent seulement l'évolution à long terme de l'orbite lunaire et de la rotation terrestre, sans aucun impact sur la rotation synchrone de la Lune.
|  | Excentricité de l'orbite = 0,0549
|  | Inclinaison orbitale par rapport au plan de l'écliptique = 5,14°
|  | Vitesse orbitale moyenne = 0,283 km/s
| Particularités :
|  | Présence d'anneaux = Non
|  | Champ magnétique = Non
|  | Albédo = Oui
|  | Présence de vie = Non

Moment cinétique d'une particule mesuré par un observateur

Le vecteur moment cinétique σC d'une particule M par rapport à un point C donné et mesuré par un Observateur O dans son Référentiel local à un instant τ est donné par la relation suivante (voir Figure ci-dessus) [GOU, Relativité Restreinte, p.322] :

P est le Vecteur impulsion de la particule.
u0 et E_u0 sont la Quadri-vitesse de l'Observateur et son Espace local de repos.
"x_u0" est l'opérateur Produit vectoriel entre deux vecteurs quelconques de E_u0, ce qui s'écrit : CM x_u0 P = Ε(u0, CM, P, .)
où :
Ε est le Tenseur de Levi-Civita
Ε(u0, CM, P, .) désigne le vecteur qui représente la Forme linéaire Ε(u0, CM, P, z) pour le Produit scalaire g.

σC appartient à E_u0 et ses composantes sont de dimension kg.m².s^-1

Multiplicité des temps propres (ou Désynchronisation des horloges parfaites)

La multiplicité des temps propres (ou désynchronisation des horloges parfaites) est la prédiction la plus extraordinaire et contre-intuitive de la Relativité (Restreinte et Générale). La version la plus étonnante de cette prédiction est le Paradoxe des jumeaux.
Cet effet fut décrit pour la première fois par Einstein en 1905 sous la forme suivante : "Si au point A, il y a deux horloges synchronisées et si nous déplaçons l'une d'elles à une vitesse constante v selon une courbe fermée qui revient à A, le déplacement étant complété en t secondes, alors à son arrivée à A, cette dernière retardera de (1/2) t (v/c)² secondes sur l'horloge immobile (en négligeant les approximations du quatrième ordre en v/c et supérieurs) [EIN Sur_l'électrodynamique, parag.4]".
Einstein indique toutefois que ce résultat est valable si "nous faisons l'ypothèse que le résultat obtenu pour une ligne polygonale est également vrai pour une ligne courbe".
Le retard indiqué par Einstein est par ailleurs une formule approchée (valable pour les vitesses faibles) [GOU, Relativité restreinte, p.47].
Ainsi, deux horloges associées à des Lignes d'univers distinctes seront en général désynchronisées lorsqu'elles se croiseront. Plus précisément, deux horloges parfaites (c'est-à-dire ne se déréglant jamais) et idéalement synchronisées vont se décaler si on les sépare avant de les réunir à nouveau. Le nombre de secondes comptée diffèrera d'une horloge à l'autre, le temps cumulé dépendant de la trajectoire suivie par chaque horloge. Si le référentiel n'est pas Inertiel, le décalage correspondra à une avance ou à un retard.

La multiplicité des temps propres est une conséquence directe de la théorie de la Relativité Restreinte. Il n'existe pas à ce jour de théorie physique alternative qui éliminerait la multiplicité des temps propres tout en respectant l'ensemble des observations empiriques validées par la Relativité restreinte [CHA][PER].

Mais qu'en est-il de l'explication rationnelle de cet effet ? Les avis sont rares et partagés, notamment :
- Pierre Spagnou, auteur scientifique, enseignant à l'ISEP, explique : "L'effet est chrono-géométrique (i.e. géométrique à quatre dimensions inséparables) : ce ne sont pas les horloges qui se dérèglent mais les "longueurs" temporelles qui ne se conservent pas lors de nos déplacements, contrairement au cadre cinématique classique" [SPA Einstein_et_la_révolution, p.23]. "C'est le nombre de secondes qui varie d'une horloge à l'autre, et non la seconde qui se contracte ou se dilate" [SPA, L'expérience].
- Henri Bergson, philosophe français, explique : "On nous dit que, si deux horloges identiques et synchrones sont au même endroit dans le système de référence, si l'on déplace l'une et si on la ramène près de l'autre au bout du temps t (temps du système), elle retardera sur l'autre horloge. Il faudrait en réalité dire que l'horloge mobile présente ce retard à l'instant précis où elle touche, mouvante encore, le système immobile, et où elle va y rentrer. Mais aussitôt rentrée, elle marque la même heure que l'autre..." [BER Durée, p.208].
- Chatgpt répond : "La relativité implique que le temps s'écoule différemment selon la vitesse de l'observateur et la présence de champs gravitationnels, ce qui se traduit par des temps propres différents pour chaque observateur. Imaginez deux randonneurs qui partent du même point de départ mais prennent des chemins différents à travers une montagne pour se retrouver à nouveau au même point à la fin de leur randonnée. Alice prend un sentier escarpé et marche sur 2 km à une vitesse moyenne de 1 km/h. Bob prend un sentier plus long mais plus plat, et marche sur 6 km à la vitesse moyenne de 2 km/h. Chacun mesure le temps qu'il a mis pour parcourir son chemin. A la fin de la randonnée, ils comparent leurs temps de marche : Alice a mis 2 heures et Bob 3 heures. Ainsi, chaque randonneur (ou observateur) a vécu son propre temps en fonction de son chemin (ou référentiel) et ces différences de temps se révèlent lorsqu'ils se rejoignent en un même point spatio-temporel." [CHA]
- Chatgpt donne également l'explication suivante sur l'expérience d'Einstein : "Même lorsque les horloges se croisent et s'arrêtent de bouger au même point, la différence de temps mesurée entre elles est due à l'effet cumulatif de la dilatation des durées pendant leur mouvement relatif précédent." [CHA]

La multiplicité des temps propres a été confirmée expérimentalement en 1971 par Hafele & Keating en même temps que la Dilation du temps gravitationnel.

Noire (énergie)

L'énergie noire est une hypothétique force répulsive globale remplissant uniformément tout l'univers, qui tend à accélérer l'expansion de l'univers (donc nécessitant : Λ > 0).
Voir Modèle cosmologique standard

Noire (matière)

La matière noire est une hypothétique matière produisant un surplus de gravité dont les galaxies ont besoin pour ne pas se défaire durant leur rotation.
Voir Modèle cosmologique standard

Notations mathématiques

Les principales notations mathématiques utilisées dans cette page sont les suivantes :

Opérations élémentaires sur les tenseurs :
Synthèse des opérateurs
, d grad div rot Δ Δ ◊ : Convention de dérivée partielle
a^km b^m ck : Convention de sommation (dite "convention d'Einstein")
; : Dérivée covariante
Div : Divergence
* : Dual (espace et base)
. ||x|| : Produit scalaire et norme
⊗ : Produit tensoriel
x : Produit vectoriel

Symboles alphabétiques grecs :
Λ : Constante cosmologique
γ : Facteur de Lorentz
ω : Forme linéaire
η : Matrice de Minkowski
Γ : Symbole de Christoffel
δ : Symbole de Kronecker
ε : Symbole de Levi-Civita
ε₀ : Permittivité diélectrique dans le vide

Symboles alphabétiques latins :
a : Rayon de l'univers
c : Vitesse de la lumière dans le vide
Ε : Tenseur de Levi-civita
E_u : Espace local de repos de l'observateur
F : Tenseur électromagnétique
g : Tenseur métrique
G : Constante de gravitation universelle
K : Coefficient de couplage gravitationnel
k : Paramètre de courbure de l'espace
O : Observateur
R : Tenseur de Ricci
R : Courbure scalaire
r* : Rayon gravitationnel
S : Tenseur d'Einstein modifié
T : Tenseur Energie-impulsion

Observateur

Un observateur O est défini par la donnée d'une Ligne d'univers L et d'un Référentiel local (e0, e1, e2, e3) le long de L (voir Figure ci-dessus) [GOU, Relativité restreinte, p.80].

La notion d'observateur est la cause de bien des incompréhensions, notamment de la part des philosophes. L'observateur relativiste ne voit pas les phénomènes au sens habituel du mot 'voir'. Il recueille des mesures de position et de temps en différents points de son référentiel. Ceci présuppose que l'on a placé en chaque point du référentiel une horloge et que cet ensemble d'horloges est synchronisé.
Une observation faite par un observateur O consiste donc à recueillir, pour un événement M qui se passe dans ce référentiel, un ensemble de valeurs pour la position (les coordonnées x, y et z) et une pour le temps (t) [MAR Mécanique p.14].

Onde gravitationnelle

Lorsqu'un objet massif se déplace dans l'espace-temps, la courbure de l'espace-temps s'ajuste pour refléter le changement de la position de l'objet.
Sous certaines circonstances, les objets accélérés peuvent produire une perturbation de l'espace-temps qui s'étend et se propage de manière analogue à des vagues à la surface de l'eau.
On désigne par onde gravitationnelle (ou parfois onde de gravitation) ce type de perturbation, et on prédit qu'elle se propage à la vitesse de la lumière.
Albert Einstein a prédit l'existence des ondes gravitationnelles en 1916. Des ondes gravitationnelles provenant de la fusion de deux trous noirs ont été détectées directement en 2015 par le laser LIGO (collaboration internationale).

Opérateurs élémentaires sur les tenseurs

Soient U, V et T des Tenseurs d'ordre quelconque et de valence quelconque portant sur les indices i,j,k,l...
En utilisant la Convention de sommation, on définit les opérations élémentaires suivantes sur ces Tenseurs :

Paradoxe des jumeaux (ou paradoxe des horloges ou voyageur de Langevin)

Dans le paradoxe des jumeaux, l'un des jumeaux reste sur Terre tandis que son frère effectue un voyage spatial à une vitesse proche de la lumière puis revient sur Terre. Il faut alors considérer trois référentiels Inertiels : celui du jumeau "au repos", celui du jumeau voyageur lors de l'aller et celui du jumeau voyageur lors du retour. Il n'est plus contesté à ce jour que les horloges des deux référentiels successifs du jumeau voyageur indiquent au total une durée plus courte que celle du jumeau au repos (Multiplicité des temps propres) et le paradoxe n'en est plus un. Peu d'auteurs cependant produisent une démonstration de ce phénomène qui soit physiquement interprétable, avec des Quadri-accélérations non infinies aux points de rupture de la trajectoire spatio-temporelle du jumeau voyageur [GOU, Relativité Restreinte, p.41].
A noter que le Principe d'équivalence combiné à la Multiplicité des temps propres prédite par la Relativité Restreinte, conduit à prédire une multiplicité de temps propres là où il y a multiplicité des potentiels gravitationnels. Deux horloges parfaites placées en des lieux de potentiels gravitationnels différents n'enregistreront pas des temps cumulés identiques. On peut parler de Paradoxe des jumeaux bis : deux jumeaux vivant à des altitudes différentes n'enregistreront pas la même durée.
Ce paradoxe montre que la Relativité permet le voyage vers le futur. Par contre, la Relativité Restreinte ne permet pas le voyage vers le passé, ce qui serait théoriquement possible en Relativité Générale en présence d'un champ gravitationnel [GOU, Relativité Restreinte, p.54].

Mais qu'en est-il du vieillissement biologique des deux jumeaux ? Peut-on dire que le jumeau voyageur revient sur Terre "plus jeune" que le jumeau sédentaire ? Les avis sont très partagés :
- Poincaré ne parle nulle part du temps biologique et affirme que "les propriétés du temps ne sont que celles des horloges".
- Einstein n'affirme rien quant au temps réellement vécu par les habitants liés à un référentiel donné.
- Thibault Damour, physicien de la Relativité, affirme que, même si le jumeau voyageur revient sur Terre plus jeune que le jumeau sédentaire, il n'en vivra pas plus longtemps pour autant. La meilleure image est celle de la cryogénie. Tout se passe comme si, au lieu d'envoyer un des jumeaux dans l'espace, on l'avait mis dans un bloc de glace puis sorti par la suite. Le temps propre du jumeau voyageur est effectivement plus court que celui du jumeau sédentaire, mais il n'acquiert pas un supplément de "temps biologique", par exemple le nombre de battements de coeur.
- Les effets de la dilatation du temps biologique sont actuellement non prouvés expérimentalement.
- La plupart des astrophysiciens affirment que parler de temps biologique n'a pas de sens scientifique.
En conclusion, l'extrapolation des effets de la dilatation du temps physique aux systèmes biologiques reste hypothétique et sujette à débat dans la communauté scientifique.

Principe d'équivalence

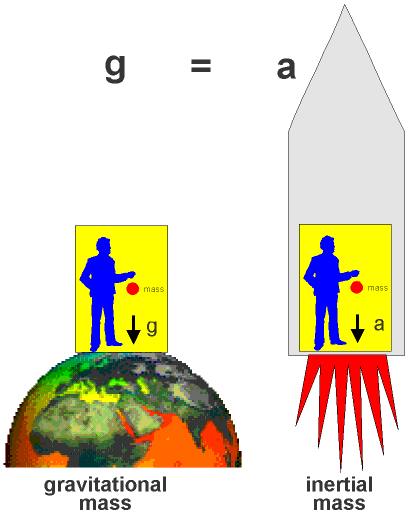
Le principe d'équivalence est un des principes fondamentaux de la Relativité Générale. Il généralise le principe Newtonien d'égalité entre masse grave (ou gravitationnelle) et masse inerte (ou inertielle) en affirmant qu'un champ de gravitation est localement équivalent à un champ d'accélération.
Il s'énonce comme suit [GOU, Relativité Restreinte, p.709] : Les mesures physiques effectuées par un Observateur Inertiel dans un champ de gravitation uniforme sont en tout point identiques aux mesures effectuées par un Observateur uniformément accéléré.

Produit scalaire et norme

Produit scalaire de deux vecteurs :

En utilisant la Convention de sommation, le produit scalaire de deux vecteurs quelconques x et y s'écrit :

où les coefficients gij sont les composantes du Tenseur métrique.
Certains auteurs utilisent également les deux autres notations suivantes :
x.y = <x, y> = g(x, y)

La norme ||x|| d'un vecteur x quelconque est la racine carrée de la valeur absolue du produit scalaire de x par lui-même :
||x|| = (|x.x|)^1/2


Produit scalaire de deux Tenseurs U et V d'ordre 2 :

T = U^ij.Vkl de composante : T = U^ij Vij
T = U^ij.V^kl de composante : T = gik gjl U^ij V^kl
T = Uij.Vkl de composante : T = g^ik g^jl Uij Vkl

Produit tensoriel

Le produit tensoriel de deux Tenseurs d'ordre m et n permet de former un Tenseur d'ordre (m + n) qui "regroupe" les deux Tenseurs.
Ainsi, le Tenseur résultant Tⁱjkl du produit tensoriel Uⁱj ⊗ Vkl a pour composantes : Tⁱjkl = Uⁱj Vkl
Le produit tensoriel conserve la nature (covariante ou contravariante) de chaque indice des tenseurs originaux.
Le produit tensoriel est associatif (U ⊗ (V ⊗ W) = (U ⊗ V) ⊗ W) (cf [GOU, Relativité restreinte, p.473]), non-commutatif et distributif par rapport à l'addition Tensorielle (U ⊗ (V + W) = U ⊗ V + U ⊗ W).

Produit vectoriel

Le produit vectoriel de deux vecteurs quelconques v et w dans un espace vectoriel à n dimensions est un Tenseur T = v x w d'ordre n-2 dont les composantes sont les suivantes :

où εi...jk est le Symbole de Levi-Civita

Espace vectoriel E de dimension 3 :
Le produit vectoriel est un vecteur T de composantes :
En composantes covariantes : Ti = εijk v^j w^k
En composantes contravariantes : Tⁱ = g^il Tl = g^il εljk v^j w^k
g^ij sont les composantes inverses du Tenseur métrique.

Espace vectoriel E de dimension 4 [GOU, Relativité Restreinte, p.87] :
Dans l'Espace local de repos de l'observateur E_u (voir Figure dans Référentiel local), le produit vectoriel (noté x_u) entre deux vecteurs quelconques v et w de E_u est un vecteur qui s'écrit : v x_u w = Ε(u, v, w, .)
où :
Ε est le Tenseur de Levi-Civita
Ε(u, v, w, .) désigne le vecteur qui représente la Forme linéaire Ε(u, v, w, z) pour le Produit scalaire g.

Quadri-accélération

La quadri-accélération ou 4-accélération d'un point quelconque x de l'Espace-temps est le Quadri-vecteur a qui mesure la variation du champ de Quadri-vitesses u le long de la trajectoire du point. Ce vecteur de dimension m^-1 est défini par la relation suivante [GOU, Relativité Restreinte, p.38] :

où τ est le Temps propre du point.
et ei sont les vecteurs de base de l'espace vectoriel de dimension 4.

Propriétés :
a est orthogonal à u : a.u = 0
a est soit le vecteur nul soit un vecteur du Genre espace : a.a ≥ 0

Quadri-courant électrique

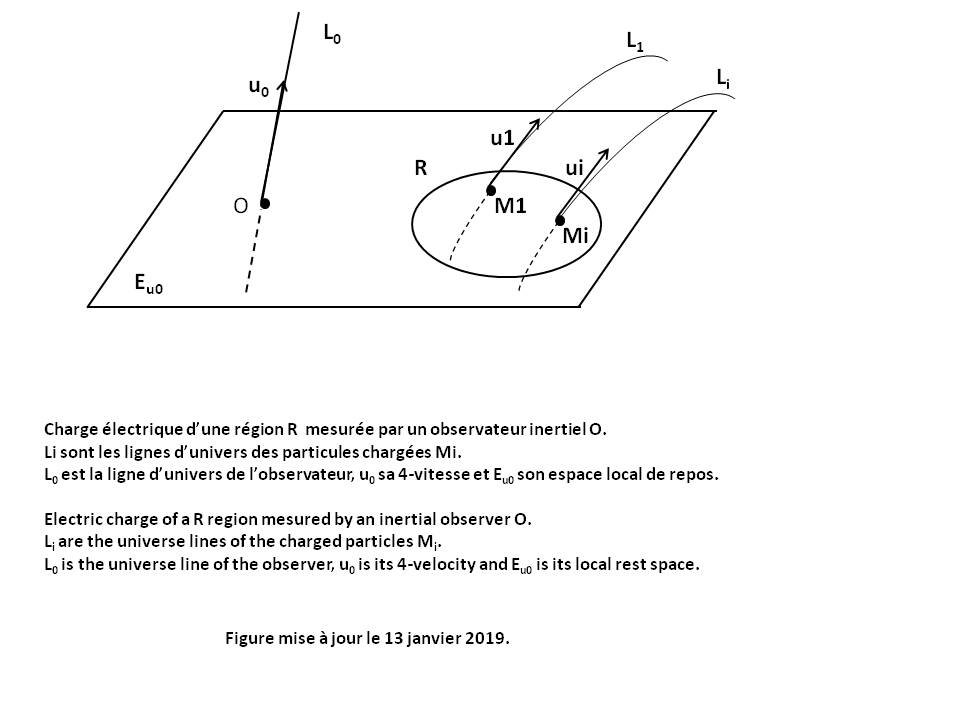
Le quadri-courant électrique ou 4-courant électrique est le Quadri-vecteur j défini par la relation suivante [GOU, Relativité Restreinte, p.580] :

Q est la charge électrique totale d'une région tridimensionnelle R dans l'Espace local de repos E_u0 d'un Observateur inertiel O de Quadri-vitesse u0. Q représente donc le flux du champ vectoriel j à travers R (voir Figure ci-dessus).
j a la dimension d'une densité volumique de charge électrique (en m^-3.A.s).

La décomposition orthogonale de j vis-à-vis de u0 s'écrit alors :

ρ est la densité de charge électrique mesurée par O (en m^-3.A.s).
J est la densité de courant électrique mesurée par O (en m^-2.A).

Quadri-force

La quadri-force ou 4-force d'une particule matérielle est le Quadri-vecteur f défini par la relation suivante [GOU, Relativité Restreinte, p.313] :

où p est la Quadri-impulsion de la particule et τ son Temps propre
Ce vecteur est de dimension N ou kg.m.s^-2.

Propriétés :
f = d(m c u)/dτ = m c² a + c (dm/dτ) u
f.u = -c (dm/dτ)

Quadri-impulsion

La quadri-impulsion ou 4-impulsion d'une particule matérielle simple (sans spin ni structure interne) est le Quadri-vecteur p défini par la relation suivante [GOU, Relativité Générale, p.37] :

où m est la masse au repos (ou masse propre) de la particule et u sa Quadri-vitesse
Ce vecteur est de dimension kg.m.s^-1 (analogue à une quantité de mouvement).

Propriété :
p.p = -m² c²