| In English | Accueil/Contact | Billard | Bélier | SNH | Relativité | Botanique | Musique | Ornitho | Météo | Aide |
| Principe | Théorie | Pratique | Annexe | Notations | Glossaire | Bibliographie | Sommaire |
Les équations de base du bélier hydraulique montrent qu'il faut maintenant établir, pour chacune des phases de fonctionnement, les expressions relatives à la vitesse v(t) de l'eau dans la conduite motrice (t étant le temps écoulé depuis le début de la phase i) et à la vitesse (vi) de l'eau en fin de phase i.
Cela permettra d'en déduire le volume (voli) véhiculé pendant la phase i et la durée (ti) de la phase i.
Une synthèse sur un cycle permettra ensuite d'établir les trois caractéristiques utiles en pratique (temps de cycle, débit moyen refoulé et rendement global) puis les conditions théoriques de fonctionnement du bélier.
Nous terminons par une comparaison du calcul avec les abaques des fabricants.
Remarques :
- Dans ce chapitre, nous nous référons aux Figures de ce chapitre, Figures du chapitre Principe, Notations.
- Les auteurs cités sont mentionnés entre crochets sous la forme [AUTEUR Titre Page]. Voir Bibliographie.
- Dans cette Bibliographie, [LAN] est l'un des seuls auteurs à avoir comparé les résultats théoriques issus de son modèle avec des mesures expérimentales.
Avertissement : pour afficher la dernière mise à jour des figures suivantes, pensez à supprimer les "fichiers temporaires" de votre navigateur Internet avant d'accéder à cette page.

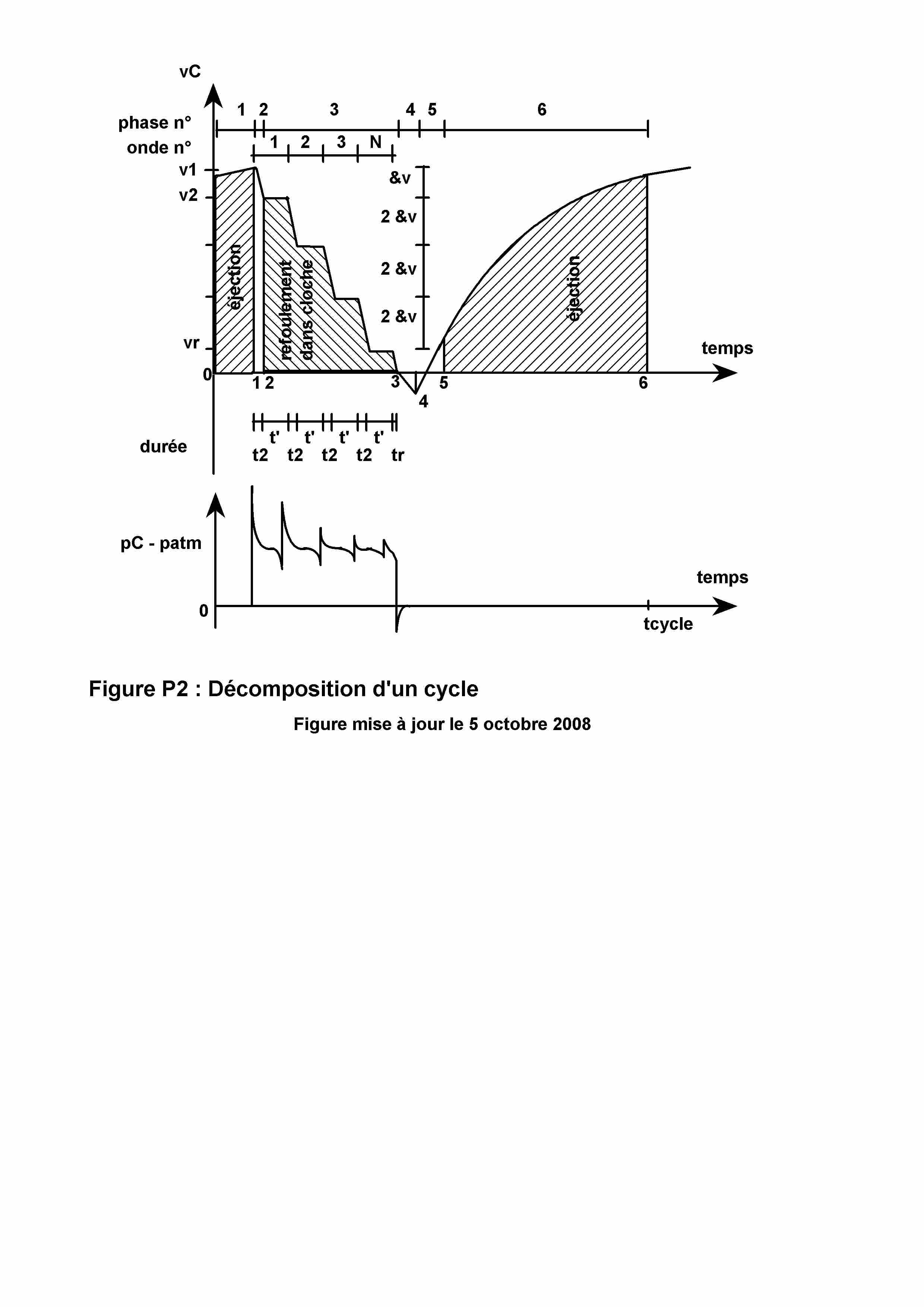
La Figure P2 ci-dessus montre la décomposition dans le temps du cycle de fonctionnement d'un bélier hydraulique.
Un premier graphique montre l'évolution de la vitesse (vC) de l'eau au point C de la conduite motrice selon six phases successives. Un second graphique montre l'évolution de la pression effective (pC - patm) en lien avec les six phases.
La phase 1 correspond à l'éjection de l'eau pendant la fermeture progressive du clapet de choc. La phase 2 correspond au début du "coup de bélier", avec ouverture du clapet de refoulement. La phase 3 correspond au refoulement de l'eau dans la cloche jusqu'à la fermeture du clapet de refoulement. Ces phases 2 et 3 montrent de manière saisissante l'existence des ondes de pression successives avec décroissance, en dent de scie, de la vitesse de l'eau au point C. La phase 4 correspond à la fin du "coup de bélier", avec retard à l'ouverture du clapet de choc. La phase 5 correspond à la mise en vitesse de l'eau dans la conduite motrice, sans éjection de l'eau. La phase 6 correspond à l'éjection de l'eau par le clapet de choc jusqu'au début de fermeture de ce dernier.
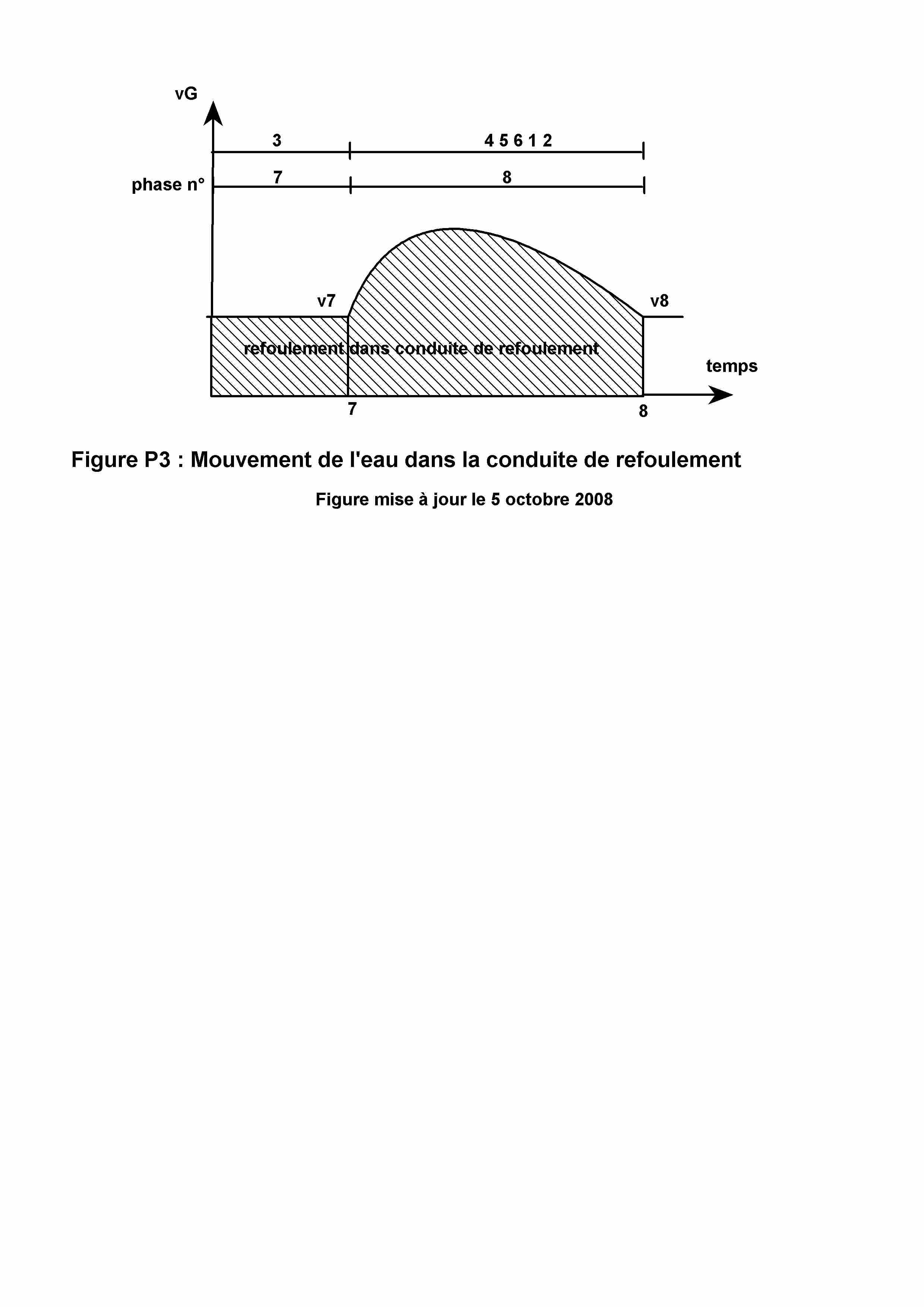
La Figure P3 ci-dessus montre l'évolution de la vitesse (vG) de l'eau au point G de la conduite de refoulement selon deux phases successives. La phase 7 s'effectue en parallèle de la phase 3, et correspond au refoulement de l'eau de la cloche dans la conduite de refoulement, le clapet de refoulement étant ouvert. La phase 8 s'effectue en parallèle de l'ensemble des phases 4, 5, 6, 1 et 2, et correspond au refoulement de l'eau de la cloche dans la conduite de refoulement, le clapet de refoulement étant fermé.
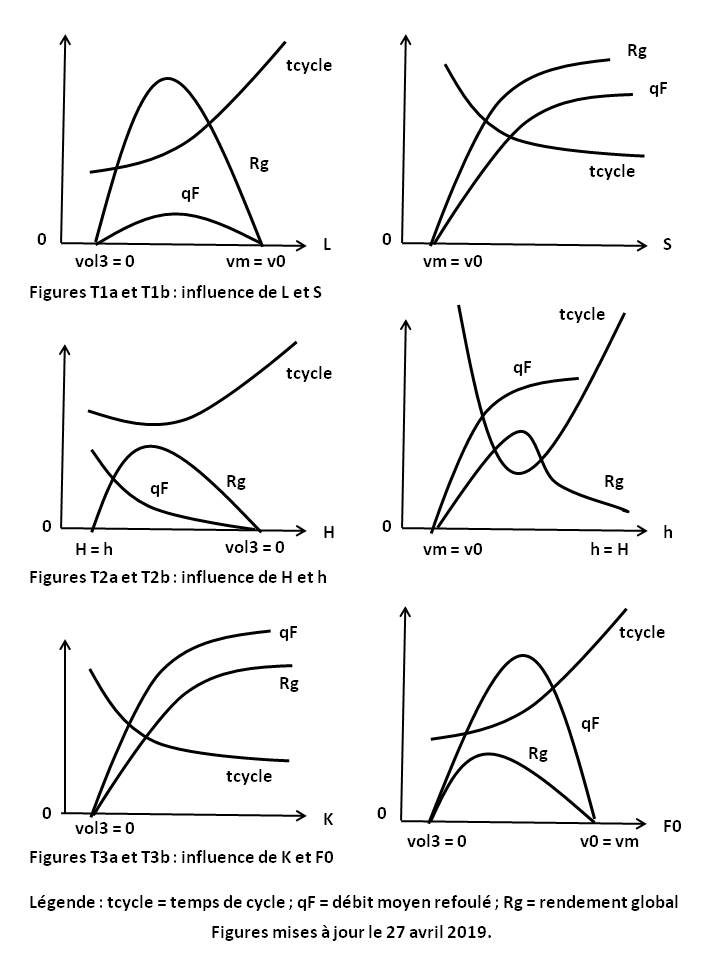
Les six Figures ci-dessus montrent l'influence de chaque paramètre du bélier hydraulique sur son temps de cycle (tcycle), son débit moyen refoulé (qF) et son rendement global (Rg).
Les Figures T1a et T1b montrent respectivement l'influence de la longueur (L) et celle de la section (S) de la conduite motrice.
Les Figures T2a et T2b montrent respectivement l'influence de la hauteur de refoulement (H) et celle de la hauteur motrice (h).
Les Figures T3a et T3b montrent respectivement l'influence de la raideur (K) du joint du clapet de choc et celle de la résistance (F0) à la fermeture du clapet de choc.
Notation : le sigle # signifie "peu différent de"
Le début du cycle correspond au début de fermeture du clapet de choc (voir Principe - Phases de fonctionnement).
A cet instant, l'ensemble des forces de pression (Fp) et de quantité de mouvement (Fh) qu'exerce l'eau sur le clapet est exactement compensée par une résistance du clapet à sa fermeture (F0) égale au poids du clapet (lorsqu'il est vertical) augmenté de la poussée du ressort de tarage (s'il existe).
Compte tenu de la relation générale [REN 7] : F = Q v2, la relation entre cette force F0 et la vitesse recherchée v0 de l'eau à cet instant est la suivante [REN 10] :
|
(T10.0) F0 = Q (v02) |
où Q est une fonction de plusieurs paramètres, notamment fonction croissante de la section droite (Sc) de l'obturateur du clapet de choc et fonction décroissante de la course totale (e0) de ce clapet [REN 8][OHA 8].
Plus précisément, on peut écrire [GUIL chapitre 2.5.1, OUZ 125] :
Fh = (débit massique) v # r Sc v2
Fp = (p amont - p aval) S = (1/2) f r v2 S
d'où l'expression approximative de Q :
|
(T10.1) Q # r S (Sc/S + f/2) |
Cette expression montre que les forces hydrodynamiques (Fh) contribuent à la fermeture du clapet de choc tout autant que les forces de pression statique (Fp).
A noter également que, pour une même force F0, toute variation de la masse volumique (r) de l'eau entraîne une variation inverse de la vitesse v0. Notamment, en période d'étiage, l'eau est moins boueuse (r plus petit) et nécessite une vitesse v0 plus importante pouvant aller jusqu'à 15 % de plus. Le clapet de choc se ferme alors plus tardivement et le bélier bat moins vite.
Par ailleurs, il faut remarquer que, pour un réglage du clapet de choc donnant le fonctionnement optimal (voir Conclusion partielle), la valeur optimale de la vitesse v0 vaut environ la moitié de la vitesse vm du régime permanent (voir Phase 6), ce qui s'écrit :
|
v0 opt # (1/2) vm |
Cette valeur remarquable de v0 servira par la suite à simplifier les calculs numériques, après linéarisation de certaines expressions autour du point de fonctionnement optimal (v0 opt).
La phase 1 de fonctionnement correspond à l'éjection de l'eau pendant la fermeture progressive du clapet de choc (voir Principe - Phases de fonctionnement).
Calcul de v(t) et v1
Certains auteurs [BER 70] ont modélisé la fermeture progressive du clapet de choc sous forme d'une variation dans le temps de la section à l'extrémité avale de la conduite motrice. La canalisation ne pouvant plus être dans ce cas considérée comme indéformable (dS/dt = 0), l'utilisation de l'équation généralisée de Bernoulli (voir Annexe - Equation du mouvement) n'est donc plus licite et les résultats obtenus par ces auteurs nous paraissent discutables. Les autres auteurs [LAN 14][OBR 14][REN 13] ont proposé d'autres modèles.
En pratique [LAN 54, 55], il s'avère que la vitesse v1 en fin de phase 1 est assez proche (à 5 % près environ) de la vitesse v0 en début de fermeture du clapet de choc. Nous retenons donc le modèle simplifié suivant :
(T11.1) v1 # v0
Concernant la vitesse v(t), elle est donc également peu différente de la valeur v0 (voir phase 1 de la Figure P2).
Calcul de vol1 et t1
En conséquence, on a [BER 83] :
(T11.2) vol1 = S ∫t10[ v dt ] # S v0 t1
Concernant le calcul de t1, si on suppose que l'accélération (J) du clapet de choc est quasiment constante et que son obturateur n'est pas rappelé par ressort (mouvement purement inertiel), le modèle s'écrit [LAN 15] :
(T11.3) t1 = (2 e0 / J)1/2
où e0 est la course totale du clapet de choc (entre les positions fermée et grande ouverte).
La valeur de J indiquée par [LAN 54] pour deux béliers différents est de l'ordre de 1 m/s2.
La phase 2 de fonctionnement correspond au début du "coup de bélier" avec ouverture du clapet de refoulement (voir Principe - Phases de fonctionnement).
Pour l'étude de cette phase, on se place au point C de la conduite motrice.
Calcul de v(t)
Le modèle du coup de bélier dit "d'ondes" [FRE 2, 5, 6][OUZ 127, 134][COM 211, 214] précise que, au passage de l'onde de choc au point C, la variation élémentaire de pression (dp) est liée à la variation de vitesse (dv) via la relation suivante :
|
(T12.0) dp / dv = - r a |
où r est la masse volumique du fluide (r = 1000 kg/m3 pour de l'eau)
a est la vitesse d'onde valant [OUZ 129, 130] :
|
(T12.0') a = 1 / (r ( KHI + (1/E)(D/e) ))1/2 |
KHI est le module de compressibilité du fluide (KHI vaut 0,5 10-9 m2/N pour de l'eau),
E le module d'élasticité longitudinal (ou module de Young) de la conduite motrice (en Giga N/m2 : E vaut 210 ; 40 ; 25 ; 3 et 1,4 respectivement pour acier & fer, fonte, béton, PVC rigide (PolyChlorure de Vinyle) et PEHD (PolyEthylène Haute Densité)),
D et e respectivement le diamètre intérieur et l'épaisseur de la conduite motrice.
Exemples : pour une conduite quasi-indéformable (ou en acier d'épaisseur suffisante) et contenant de l'eau, la vitesse d'onde (a) vaut environ 1300 m/s ; pour une conduite en PVC rigide de rapport (D/e) valant environ 50 ou une conduite en PEHD de rapport (D/e) valant environ 20, la vitesse d'onde vaut environ 240 m/s.
Si on suppose que le joint du clapet de choc est sensiblement élastique (de coefficient de raideur K), alors la variation de pression (dp) dans le clapet est liée à la variation (dvol) de volume d'eau due à la compression du joint par les relations suivantes :
dvol / Sc = dF / K
dp = dF / Sc = Y dvol
Y est une caractéristique de l'ensemble obturateur-joint du clapet de choc valant (en N/m5), après remplacement :
(T12.0'') Y = K / (Sc)2
Remarque : Les valeurs de K pour chacun des deux béliers étudiés par [LAN 54] sont respectivement 56 106 N/m et 7 106 N/m.
Par ailleurs, cette variation de volume (dvol) est reliée au temps (t) par la relation suivante :
dvol = S v dt
Après remplacements, on obtient alors la relation liant la vitesse (v) au temps (t) :
dt = - Z dv / v
Ce qui s'écrit également [LAN 18] :
(T12.1) v(t) = v1 e-t/Z
(T12.1') Z = (r/Y)(1/S)a
Remarque : La caractéristique Z (en seconde) s'apparente à une constante de temps dans la loi T12.1
La relation (T12.1) montre que la vitesse v(t) est donc une fonction décroissante de t (voir phase 2 de la Figure P2).
Calcul de v2
Concernant la vitesse v2 en fin de phase 2, elle vaut naturellement :
(T12.2) v2 # v1 - &v
où &v est la perte moyenne de vitesse v à chaque réflexion de l'onde de choc aux points A et F (voir Phase 3).
Calcul de t2
La durée t2 de la phase se déduit de la relation (T12.1) :
(T12.3) t2 = Z ln[ v1 / v2 ]
ce qui s'écrit encore, compte tenu de la relation (T12.2) :
(T12.4) t2 = -Z ln[ 1 - (&v / v1) ]
Simplification de t2
En remarquant que le ratio (&v / v1) est petit devant 1 en pratique (voir (T33.2)), la relation (T12.4) se linéarise sous la forme :
(T12.5) t2 # Z (&v / v1)( 1 + (1/2)(&v / v1) )
La phase 3 de fonctionnement correspond au refoulement de l'eau dans la cloche à air avec fermeture du clapet de refoulement (voir Principe - Phases de fonctionnement).
Calcul de v(t)
Comme la phase 2 précédente, la phase 3 est supposée suivre le modèle du coup de bélier dit "d'ondes" [COM 211][FRE 2, 5, 6][OUZ 134].
Créée par la fermeture brusque du clapet de choc en début de phase 2, l'onde de pression se propage dans la conduite motrice avec une vitesse constante (a) et vient se réfléchir alternativement d'une extrémité ouverte du tube d'eau à l'autre, entre les points A (à la surface du niveau d'eau du collecteur) et F (au-dessus du clapet de refoulement resté ouvert, à la surface du niveau d'eau dans la cloche à air). A chaque passage de l'onde en F et en A, la vitesse v dans la conduite motrice subit une petite perte de vitesse &v. La vitesse v(t) au point C de la conduite motrice est alors une fonction décroissante, en dent de scie, du temps t (voir phase 3 de la Figure P2).
Plus précisément, le phénomène est le suivant [LAN 19][REN 18] :
La première onde engendrée par la fermeture du clapet de choc atteint le clapet de refoulement quasi-immédiatement. Dès que la pression motrice au point C devient suffisante, le clapet de refoulement s'ouvre (de façon supposée instantanée) et l'eau de la conduite motrice commence à envahir la cloche à air (fin de la phase 2). Au point C, si (&v)1 désigne la perte de la vitesse initiale (v1) de l'eau, la vitesse de l'eau vaut alors ( v1 - (&v)1 ).
En négligeant la résistance à la fermeture du clapet de refoulement en fin de phase 2 (comprenant le poids du clapet avec lest éventuel et force de compression du ressort), la surpression (&p)1 nécessaire pour ouvrir le clapet de refoulement doit être un peu supérieure à la différence de pression initiale, compte tenu de la perte de charge singulière (coefficient fr) à travers le clapet de refoulement. La valeur de (&p)1 est donnée par l'équation de Bernoulli (voir Annexe - Equation du mouvement) appliquée au filet de courant entre les points C et F :
(T13.0) (&p)1 = r g (H - h) + (1/2) fr r ( v1 - (&v)1 )2
avec :
(&v)1 < v1
Le modèle du coup de bélier dit "d'ondes" donne par ailleurs :
(T13.1) (&p)1 = r a (&v)1
Ce qui permet le calcul exact de (&v)1 et de (&p)1, si nécessaire.
L'onde de pression se propage ensuite à la vitesse (a) jusqu'au collecteur. Cette onde incidente se réfléchit alors sur la surface ouverte de l'eau (au point A), ce qui a pour conséquence [FRE 7] de changer le signe de la variation de pression ((&p)1 > 0), sans changer le signe de la variation de vitesse de l'eau (-(&v)1 < 0).
La vitesse de l'eau pendant le retour de l'onde vaut donc : v1 - 2 (&v)1
Le clapet de refoulement, au moment où la dépression l'atteint, tend à se fermer, mais l'onde incidente se réfléchit en F et engendre une seconde onde de pression. La vitesse de l'eau au point C subit alors une perte (&v)2 et devient égale à : v1 - 2 (&v)1 - (&v)2.
Cette deuxième onde remonte jusqu'au collecteur et le phénomène se reproduit plusieurs fois jusqu'à ce que la vitesse de l'eau soit insuffisante pour maintenir ouvert le clapet de refoulement.
Les mesures de pression (p) réalisées par [REN 20][OBR 49] montrent de manière saisissante l'existence des ondes de pression-dépression successives (voir Figure P2).
Il reste maintenant à préciser, au point C, l'expression de la vitesse v(t) avant, pendant et après le passage de chaque onde de choc.
Pour simplifier les calculs, on suppose que toutes les variations de pression (&p)1, (&p)2... (&p)N au passage de chaque onde sont identiques en amplitude.
La variation moyenne (&p) est donc la moyenne arithmétique entre la variation de pression initiale (&p)1 et la variation de pression finale (&p)N, cette dernière valant : r g (H - h). Compte tenu de (T13.0)(T13.1), la perte moyenne de vitesse (&v) à chaque réflexion de l'onde vaut donc :
&v # (g/a) (H - h) + (1/4) fr (1/a)(v12)( 1 - (&v / v1) )2
Pour un ratio (&v / v1) petit devant 1 en pratique (voir (T33.2)), le dernier terme vaut environ : ( 1 - 2 (&v / v1)) et l'expression &v se simplifie en :
(T13.2) &v # ( g (H - h) + (1/4) fr (v12) ) / (a + (1/2) fr v1)
En posant :
(T13.4) U = ( H/h - 1 + (1/4) fr (1/g)(1/h)(v12) ) / ( 1 + (1/2) fr (v1 / a) )
alors la relation (T13.2) s'écrit plus simplement :
(T13.2') &v # U h g/a
En pratique, la relation (T13.4) est très proche de :
|
(T13.4') U # H/h - 1 |
Si N désigne le nombre entier d'ondes aller et retour durant les phases 2 et 3, on démontre facilement que (voir Figure P2) :
(T13.5) N = Partie_entière[ (1/2)(v1 + &v) / &v ] = Partie_entière[ (1/2)(v1 / &v)( 1 + (&v / v1) ) ]
Pour un ratio (&v / v1) petit devant 1 en pratique (voir (T33.2)), le nombre N s'écrit :
(T13.5') N # (1/2)(v1 / &v) > 1/2
La Figure P2 montre également que chaque onde successive 1, 2... N se compose d'une décroissance de la vitesse v(t) de durée totale (t2), suivie d'un palier horizontal de durée totale (t').
La durée totale de chaque onde aller et retour valant approximativement (2 L/a), on a de plus la relation :
(T13.7) t' # 2 (L/a) - t2 > 0
Pour l'onde 1, la décroissance de la vitesse v(t) est connue (voir relation(T12.1)).
Pour chaque onde 2, 3... N, la décroissance élémentaire (dv) résulte de l'onde incidente immédiatement suivie de l'onde réfléchie, et vaut donc le double de la décroissance élémentaire (dv) pour l'onde 1.
D'où l'expression de la vitesse v(t) au point C et pour chaque segment de courbe (avec t pris à 0 au début de chaque segment) :
Onde 1 :
phase 2 pour rappel : v(t) = v1 e-t/Z
v(palier) = v2 = v31 = v1 - &v
Onde 2 (décroissance puis palier) :
v(t) = v31 - 2 v1 ( 1 - e-t/Z )
v(palier) = v32 = v31 - 2 &v = v1 - 3 &v
...
Onde N (décroissance puis palier) :
v(t) = v3(N-1) - 2 v1 ( 1 - e-t/Z )
(T13.8) v(palier) = vr = v3N = v3(N-1) - 2 &v = v1 - (2 N - 1) &v
Onde N+1 (début d'onde avec décroissance sur une durée résiduelle tr) :
v(t) = v3N - 2 v1 ( 1 - e-t/Z )
Calcul de v3 et tr
La vitesse v3 en fin de phase 3 est très petite et peut être prise à :
(T13.3) v3 # 0
Sachant qu'on a : v(tr) = v3 pour l'onde N+1, on en déduit la durée résiduelle (tr) :
(T13.9) tr = Z ln[ 2 v1 / (2 v1 - vr) ]
Calcul de vol3 et t3
Le volume vol3 véhiculé durant la totalité de la phase 3 vaut :
vol3 = S ∫durée_phase3[ v dt ]
D'où, après calculs, l'expression de vol3 pour chaque segment de courbe (voir également [LAN 26]) :
Onde 1 :
vol3 / S = v31 t' = (v1 - &v) t'
Onde 2 :
vol3 / S = 2 Z &v - (v1 + &v) t2 + (v1 - 3 &v) t'
...
Onde N :
vol3 / S = 2 Z &v - (v1 + (2 N - 3) &v) t2 + (v1 - (2 N - 1) &v) t'
Onde N+1 :
vol3 / S = Z vr - (2 v1 - vr) tr
La volume vol3 pour la phase 3 est donc la somme de ces termes et peut se mettre sous la forme :
(T13.6) vol3 = S (A + B + C + D)
avec :
A = 2 (N - 1) Z &v + Z vr
B = N t' (v1 - N &v)
C = - (N - 1) t2 ( v1 + (N - 1) &v )
D = - (2 v1 - vr) tr
En utilisant la relation (T13.5'), la relation (T13.8) devient :
(T13.8') vr # &v
En utilisant cette dernière relation, la relation (T13.9) devient :
tr # -Z ln[ 1 - (1/2)(&v / v1) ]
Pour un ratio (&v / v1) petit devant 1 en pratique (voir (T33.2)), cette dernière relation se linéarise en :
(T13.9') tr # (1/2) Z (&v / v1)( 1 + (1/4)(&v / v1) )
L'ensemble des relations (T12.5)(T13.5')(T13.6)(T13.7)(T13.8')(T13.9') donne, après remplacements :
(T13.10) vol3 # (1/2) S v1 ( (L/a)(v1 / &v) - Z (&v / v1) )
Remarque : pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), compte tenu des relations (T13.2')(T11.1), le volume vol3 serait maximal et égal à :
(T13.10') vol3 maxi # (1/2) S v0 (T/U)
Concernant la durée t3 de la phase, elle vaut (voir Figure P2) :
(T13.11) t3 # 2N (L/a) - t2 + tr
ce qui se s'écrit encore, compte tenu des relations (T13.5')(T12.5)(T13.9') :
(T13.11') t3 # (L/a)(v1 / &v) - (1/2) Z (&v / v1)
Comparaison avec le modèle de la colonne résistante constante
Le modèle de la colonne résistante constante (voir Annexe) donne pour équation de la vitesse v(t) [BER 85] :
(T13.12) H = h - (1/2) j3 (1/g)(v2) - L (1/g)(dv/dt)
avec :
(T13.13) j3 = 1 + fr + u L/D
où fr est le coefficient de perte de charge singulière du clapet de refoulement, u le coefficient de perte de charge linéaire de la conduite motrice, L sa longueur et D son diamètre.
Le coefficient u varie généralement de 0,02 à 0,03 [REN 5][OUZ 224].
Le coefficient fr dépend des incidents de parcours du fluide autour du clapet [OUZ 140], et notamment de la course totale (e') du clapet de refoulement entre les positions complètement ouverte (fr > 3 en général [GUIL chapitre 1.4.7]) et complètement fermée (fr = ∞).
En désignant par v'm la vitesse particulière suivante :
(T13.14) v'm = (2 (1/j3) g (H - h))1/2
et en effectuant le changement de variable :
(T13.15) w' = v / v'm ; w'1 = v1 / v'm ; w'3 = v3 / v'm
alors la relation (T13.12) se met sous la forme simple :
(T13.16) dw'/dt = -(1/2) j3 (v'm / L)(1 + w'2)
La résolution de cette équation différentielle donne alors les relations t(w') ou w'(t) suivantes :
(T13.17) t(w') = y' ( Arctg[w'1] - Arctg[w'] )
(T13.18) w'(t) = ( w'1 - tg[ t/y'] ) / ( 1 + w'1 tg[ t/y'] )
avec :
(T13.19) y' = 2 (1/j3)(L / v'm)
La relation (T13.18) montre que la vitesse v(t) est donc une fonction décroissante de t (voir phase 3 de la Figure P2) qui s'annule pour :
(T13.20) t3 = 2 (1/j3)(L / v'm) Arctg[w'1]
Le volume vol(t) véhiculé depuis le début de la phase 2 jusqu'au temps t s'écrit :
vol(t) = S ∫t0[ v dt ]
ou encore, en utilisant la relation (T13.16) :
vol(t) = S ∫w'w'1[ -2 (1/j3) L w' dw' / (1 + w'2) ]
Cette expression s'intègre en :
vol(t) = (1/j3) S L ( ln[ 1 + w'12 ] - ln[ 1 + w'2 ] )
d'où :
(T13.21) vol3 = (1/j3) S L ln[ 1 + w'12 ]
Nous pouvons maintenant comparer le modèle de la colonne résistante constante avec celui du coup de bélier, en se plaçant pour simplifier dans le cas d'un joint relativement rigide du clapet de choc (K grand donc Z = 0) et d'un clapet de refoulement sans perte de charge singulière (fr = 0).
Dans ce cas, on considère le rapport Rt des durées t3 entre les deux modèles (T13.20) et (T13.11'), ainsi que le rapport Rv des volumes vol3 entre les deux modèles (T13.21) et (T13.10). Compte tenu de (T13.2') et (T13.4'), ces deux rapports valent respectivement :
Rt = Arctg[w'1] / w'1
Rv = ln[ 1 + w'12 ] / w'12
Compte tenu de (T11.1), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), et en supposant pour simplifier que les pertes de charge singulières des clapets de choc et de refoulement ont même valeur (j = j3), alors la valeur w'1 vaut :
w'1 = v1 / v'm # (1/2) / (H/h - 1)1/2
Les deux rapports Rt et Rv sont alors proches de la valeur 1 à 5 % près au maximum.
Pour un rapport de hauteurs H/h pas trop petit (supérieur à 3), les deux modèles sont donc quasi-équivalents dans le cas simplifié considéré ici. Le modèle du coup de bélier présenté en début de ce chapitre est par contre plus précis dans le cas général, notamment pour rendre compte des conditions de fonctionnement d'un bélier (voir Synthèse).
La phase 4 de fonctionnement correspond au retard au début d'ouverture du clapet de choc (voir Principe - Phases de fonctionnement).
Calcul de v(t), v4 et t4
A la fin du "coup de bélier" (juste après la fermeture du clapet de refoulement), la vitesse de l'eau au point C est très faible. La dernière onde descendante (N) dans la conduite motrice (onde de dépression) atteint le point C en diminuant encore cette vitesse et provoque un éventuel recul de l'eau vers le collecteur. En outre, cette onde incidente se réfléchit sur la surface fermée du clapet de refoulement, ce qui a pour conséquence [FRE 7] de changer le signe de la variation de vitesse de l'eau ((&v)N > 0), sans changer le signe de la variation de pression ((&p)N < 0). La nouvelle dépression au point C fait passer la pression de l'eau sous la pression atmosphérique qui provoque alors l'aspiration d'un peu d'air par le reniflard et l'ouverture quasi-instantanée du clapet de choc.
La vitesse v(t) durant cette phase est mal connue (voir phase 4 de la Figure P2).
Concernant la vitesse v4 en fin de phase 4, [LAN 29] propose un modèle basé sur l'énergie cinétique de l'eau dans la conduite motrice et l'énergie stockée dans la compression du joint du clapet de choc, lesquelles produisent ensemble en fin de phase 4 une vitesse v4 égale à :
(T14.1) v4 = - ((v32) + Z (a/L)(&v2))1/2
(T14.2) t4 # - 2 Z &v / (v3 + v4)
Compte tenu de la relation (T13.3), les relations (T14.1)(T14.2) se simplifient en :
(T14.1') v4 # - &v (Z a/L)1/2
(T14.2') t4 # 2 (Z L/a)1/2
La phase 5 de fonctionnement correspond à la mise en vitesse de l'eau sans éjection (voir Principe - Phases de fonctionnement).
Calcul de v(t)
L'eau remontant dans la conduite motrice, l'ouverture du clapet de choc a pour effet de réduire progressivement cette vitesse, de l'annuler puis de l'inverser. L'eau redescend alors normalement dans la conduite motrice, sans qu'il y ait encore éjection de l'eau par le clapet de choc.
Cette phase se modélisant bien par une colonne résistante constante de hauteur h (voir Annexe), les équations sont similaires à celles trouvées en phase 3 pour une colonne résistante constante, en remplaçant H par 2h, j3 par j et v par -v. L'équation de la vitesse v(t) s'écrit alors [REN 25][OBR 27] :
(T15.1) h = - (1/2) j (1/g)(v2) + L (1/g)(dv/dt)
En effectuant le changement de variable :
(T15.2) w = -v / vm ; w4 = -v4 / vm > 0 ; w5 = -v5 / vm
alors la relation (T15.1) se met sous la forme simple :
(T15.3) dw/dt = -(1/2) j (vm / L)(1 + w2)
Remarque : la forme de cette relation est similaire à celle de la relation (T13.16).
La résolution de cette équation différentielle donne alors les relations t(w) ou w(t) suivantes :
(T15.4) t(w) = y ( Arctg[w4] - Arctg[w] )
(T15.5) w(t) = ( w4 - tg[ t/y ] ) / ( 1 + w4 tg[ t/y ] )
avec :
(T15.6) y = 2 (1/j)(L / vm)
La relation (T15.5) montre que la vitesse v(t) est donc une fonction croissante de t (voir phase 5 de la Figure P2).
Calcul de v5
Concernant la vitesse v5 en fin de phase 5, il est raisonnable de poser [LAN 34] :
(T15.7) v5 # -v4
Calcul de t5
Concernant la durée t5 de la phase, la relation (T15.4) donne :
(T15.8) t5 = 2 (1/j)(L / vm)( Arctg[w4] - Arctg[w5] )
ou encore, en tenant compte de (T15.7) :
(T15.8') t5 # 4 (1/j)(L / vm) Arctg[w4]
Simplification de t5
En remarquant que w4 est petit en pratique devant 1 (voir relation (T14.1')), la durée t5 se linéarise sous la forme :
(T15.8'') t5 # 4 (1/j)(L / vm) w4 = 2 (1/g)(L/h)(-v4)
On retrouve pour t5 la même expression que [LAN 34] qui a utilisé par ailleurs un autre modèle pour v(t).
La phase 6 de fonctionnement correspond à l'éjection de l'eau avec clapet de choc complètement ouvert (voir Principe - Phases de fonctionnement).
Calcul de v(t)
Tous les auteurs sont unanimes pour prendre le modèle d'une mise en eau de la conduite motrice par colonne motrice constante (voir Annexe). D'où l'équation de la vitesse v(t) [LAN 34][OBR 11][BER 65] [REN 4][OUZ 116] :
(T16.1) h = (1/2) j (1/g)(v2) + L (1/g)(dv/dt)
avec :
|
(T16.2) j = 1 + f + fh + u L/D |
où f est le coefficient de perte de charge singulière du clapet de choc, fh le coefficient global de perte de charge singulière hors perte induite par le clapet de choc, u le coefficient de perte de charge linéaire de la conduite motrice, L sa longueur et D son diamètre.
Le coefficient u varie généralement de 0,02 à 0,03 [REN 5][OUZ 224].
|
Le coefficient fh rend compte des différents incidents de parcours le long de toute la conduite motrice (hors clapet de choc) et est égal à la somme des coefficients de perte de charge singulière relatifs aux obstacles suivants [OUZ 140-142] : - la crépine située à l'extrémité amont de la conduite motrice, dont le coefficient vaut entre 2 et 4 pour une crépine en tôle perforée ; - la vanne de réglage dont le coefficient vaut, en position grande ouverte, entre 0,05 et 0,4 selon le type de vanne ; - des raccordements de type manchon dont le coefficient vaut environ 0,05 par raccordement ; - chacune des extrémités de la conduite motrice (cas particuliers du rétrécissement ou de l'évasement brusques) pour lesquelles le coefficient vaut environ 0,5 pour l'entrée et 1 pour la sortie ; - d'éventuels coudes à angle droit, dont le coefficient vaut 1 pour un coude "brusque" (dont le rayon de courbure est inférieur à D/2) et environ 0,2 pour un coude convenablement arrondi [OUZ 141] ; - d'éventuels rétrécissements ou élargissements progressifs de section, dont les coefficients dépendent de l'angle du convergent ou du divergent. Voir [OUZ 141]. |
En pratique, le coefficient fh minimal (correspondant à une vanne de réglage grande ouverte et à la présence d'une crépine) peut être pris à : fh # 6
| Le coefficient f dépend des incidents de parcours du fluide autour du clapet [OUZ 140], et notamment de la course totale (e0) du clapet de choc entre les positions complètement ouverte (f > 3 en général [GUIL chapitre 1.4.7]) et complètement fermée (f = ∞). |
Les fabricants de clapets et de vannes utilisent plutôt le coefficient de débit Kv (cf Données techniques Joucomatic et exemple SALVI_clapet_4093M (.pdf, 950 Ko)) sous la forme suivante :
|
(T16.2b) Kv # S v ( (r / r_ref)/(&p / &p_ref) )1/2 |
où _ref est le résultat d'un test de référence.
En Europe, Kv est exprimé en m3/h avec r_ref = r eau à 20°C et &p_ref = 1 bar.
Aux USA, on utilise plutôt le coefficient de débit Cv exprimé en gallon US par minute (1 gallon US = 3,7854 10-3 m3) avec &p_ref = 1 psi = 0,06895 bar et r_ref = r eau à 60°F
D'oû la relation : Cv (en gallon US /mn) / Kv (en m3/h) = (60 / 3,7854 10-3) (1/3600) ( (r_20°C/r_60°F) / (&p_1bar/&p_1psi) )1/2
Compte tenu de la conversion : T(°C) = (5/9) (T(°F) - 32), cela donne l'équivalence :
|
(T16.2c) Cv = 1,156 Kv |
A noter que l'on trouve parfois dans la documentation scientifique la relation inverse (Kv = 1,156 Cv) qui est erronée. C'est le cas de l'article [SER 22].
La pression différentielle &p s'écrivant par définition :
(T16.2d) &p = (1/2) f r v2
alors on peut exprimer simplement f en fonction de Kv :
(T16.2e) f # 2 (&p_ref / r_ref) (S / Kv)2
D'où finalement :
|
(T16.2f) f # 2 ( 36000 S / (Kv en m3/h) )2 |
Lorsqu'on maintient ouvert le clapet de choc pendant le mouvement de l'eau dans la conduite motrice, la relation (T16.1) permet d'exprimer la vitesse de l'eau (vm) lorsque le régime permanent est atteint (dv/dt = 0) :
|
(T16.3) vm = (2 (1/j) g h)1/2 |
En effectuant le changement de variable :
(T16.4) w = v / vm ; w5 = v5 / vm ; w6 = v6 / vm
alors la relation (T16.1) se met sous la forme simple :
(T16.5) dw/dt = (1/2) j (vm / L)(1 - w2)
La résolution de cette équation différentielle donne alors les relations t(w) ou w(t) suivantes :
(T16.6) t(w) = (1/2) y ( ln[ (1 + w)/(1 - w) ] - ln[ (1 + w5)/(1 - w5) ] )
(T16.7) w(t) = (eA - 1) / (eA + 1)
avec :
(T16.8) A = 2 (t/y) + ln[ (1 + w5)/(1 - w5) ]
et y donné par (T15.6).
La relation (T16.7) montre que la vitesse v(t) est donc une fonction croissante de t (voir phase 6 de la Figure P2).
Calcul de v6
Concernant la vitesse v6 en fin de phase 6, elle coincide avec le début de la phase 1 du cycle suivant, d'où :
(T16.9) v6 = v0
Calcul de vol6 et t6
Le volume vol(t) véhiculé depuis le début de la phase jusqu'au temps t s'écrit :
vol(t) = S ∫t0[ v dt ]
ou encore, en utilisant la relation (T16.5) :
vol(t) = S ∫ww5[ 2 (1/j) L w dw / (1 - w2) ]
Cette expression s'intègre en :
vol(t) = (1/j) S L ln[ (1 - w52) / (1 - w2) ]
d'où :
(T16.10) vol6 = (1/j) S L (M6 - M5)
Mi = ln[ 1/(1 - wi2) ]
Concernant la durée t6 de la phase, la relation (T16.6) donne :
(T16.11) t6 = (1/j)(L / vm)(N6 - N5)
Ni = ln[ (1 + wi)/(1 - wi) ]
Ces résultats sont équivalents à ceux des auteurs [LAN 36][OBR 30][BER 67][REN 11], les deux derniers auteurs ayant pris w5 a priori égal à zéro.
Simplification de vol6 et t6
Pour les besoins ultérieurs de cette étude, il est nécessaire de simplifier les expressions trouvées pour vol6 et t6.
En remarquant que w52 et w5 sont petits en pratique devant 1 (voir relations (T15.7) et (T14.1')), on a :
M5 # w52
N5 # 2 w5
Par ailleurs, compte tenu de (T16.9), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), les expressions M6 et N6 se linéarisent autour du point de fonctionnement w6 = 1/2 et w62 = 1/4 sous la forme :
M6 # (4/3) (w6 opt)2 - ln[3/4] - 1/3 # (4/3) (w6 opt)2
N6 # (8/3) (w6 opt) + ln[3] - 4/3 # (8/3) (w6 opt)
D'où finalement :
(T16.10') vol6 # A - (1/2) S (1/g)(L/h)(v52)
(T16.11') t6 # B - (1/g)(L/h) v5
avec A et B valant respectivement, compte tenu de (T16.3)(T16.4)(T16.9) :
A # (1/j) S L M6 # (2/3)(1/g)(L/h) S (v0 opt)2
B # (1/j)(L / vm) N6 # (4/3)(1/g)(L/h) (v0 opt)
ou bien
A = (1/j) S L ln[ 1/(1 - (v0 / vm)2) ]
B = (1/j)(L / vm) ln[ ( 1 + (v0 / vm) )/( 1 - (v0 / vm) ) ]
selon que v0 est maintenu constant ou non autour de la valeur v0 opt (T26.0).
Nous verrons plus tard (voir Synthèse) l'importance des derniers termes v52 et v5 sur le rendement global.
(T16.12) Remarque : Compte tenu des notations (T21.2)(T26.5) et de la relation (T16.3), les expressions A et B s'écrivent :
A / (S v0 T) = (1/2) (1 / x2) ln[ 1/(1 - x2) ] # 2/3
B / T = (1/2) (1/x) ln[ (1 + x)/(1 - x) ] # 4/3
Cette simplification des expressions A et B introduit une erreur relative de moins de 20 % pour toute valeur de x comprise entre 1/2 et 4/5.
Calcul de (dv/dt)(t6)
Plus tard (voir Phase 1), nous aurons éventuellement besoin de l'expression de l'accélération dv/dt de l'eau en fin de phase 6. En utilisant la relation (T16.5), on trouve :
(T16.13) (dv/dt)(t6) = g (h/L)(1 - (v6 / vm)2)
La phase 7 de fonctionnement correspond au refoulement de l'eau de la cloche dans la conduite de refoulement, le clapet de refoulement étant ouvert (voir Principe - Phases de fonctionnement).
On appelle (v) la vitesse de l'eau dans la conduite de refoulement à tout instant (t) de cette phase.
Calcul de t7
La durée t7 est égale à la durée pendant laquelle le clapet de refoulement reste ouvert, soit :
(T17.1) t7 = t3
avec t3 donné par (T13.11').
Remarque : Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), la relation (T17.1) se simplifie en :
(T17.1') t7 # (T opt) / U
avec T opt donné par (T21.2).
Application numérique : si h = 3 m ; H = 30 m ; L = 20 m ; j = 15 ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
T opt = 0,68 s
t7 # 0,076 s
Calcul de v(t) et v7
En pratique, il s'avère que la vitesse v7 en fin de phase 7 est assez proche de la vitesse v8 en fin de phase précédente 8, l'inertie de la colonne d'eau H n'ayant pas le temps de modifier cette vitesse durant la compression de l'air de la cloche. Nous retenons donc le modèle simplifié suivant :
(T17.2) v7 # v8
Concernant la vitesse v(t), elle est donc également peu différente de la valeur v7 (voir phase 7 de la Figure P3).
Calcul de vol7
En conséquence, on a :
(T17.3) vol7 = S' ∫t70[ v dt ] # S' v7 t7
La phase 8 de fonctionnement correspond au refoulement de l'eau de la cloche dans la conduite de refoulement, le clapet de refoulement étant fermé (voir Principe - Phases de fonctionnement).
On appelle (v) la vitesse de l'eau dans la conduite de refoulement à tout instant (t) de cette phase.
Calcul de t8
La durée t8 est égale à la durée pendant laquelle le clapet de refoulement reste fermé, soit :
(T18.1) t8 = t4 + t5 + t6 + t1 + t2 = tcycle - t3
Remarque : Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), cette relation se simplifie, compte tenu de (T21.1), en :
(T18.1') t8 # (T opt)(4/3) + t1
Application numérique : si h = 3 m ; H = 30 m ; L = 20 m ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
T opt = 0,68 s
t8 # 1,0 s
Calcul de v(t)
Pour trouver la vitesse v(t), il est nécessaire de connaître l'évolution dans le temps de la pression (pF) et du volume d'air comprimé (volair) situé dans la cloche. En assimilant cet air à un gaz parfait et la détente de l'air à une transformation isotherme durant la phase 8, alors pF et volair sont liés à tout instant (t) par la relation suivante :
(T18.2) pF(t) = pF7 volair7 / volair(t)
dans laquelle :
pF7 et volair7 sont respectivement la pression et le volume d'air comprimé en fin de phase 7,
pF7 est donné par la relation (T18.63),
volair7 est donné par la relation suivante, compte tenu du volume d'air de la cloche (volairatm) à la pression atmosphérique (patm) c'est-à-dire au démarrage du bélier :
(T18.3) volair7 = volairatm patm / pF7
On appelle (zF) l'altitude du point F situé à l'interface air-eau de la cloche, et (Si) la section intérieure de cette cloche. La variation du volume d'air comprimé (volair) à tout instant (t) s'écrit alors :
(T18.4) d(volair)/dt = (-Si) d(zF)/dt
Par ailleurs, la conservation du débit massique de l'eau dans la conduite de refoulement (voir Annexe - Equation de continuité - Remarque 2) appliquée entre les points F et G de cette conduite s'écrit :
(T18.5) r (-Si) d(zF)/dt = r S' v(t)
Enfin, le mouvement de l'eau entre ces deux points suit l'équation généralisée de Bernoulli (voir Annexe - relation (A16)) et s'écrit :
(T18.6) pF(t) + r g zF(t) + (1/2) r (d(zF)/dt)2 = patm + r g zG + (1/2) r j8 (v(t))2 + r L' dv/dt
avec :
(T18.7) j8 = 1 + (f8 + u' L' / D') Signe[v(t)]
où f8 est le coefficient global de perte de charge singulière de la conduite de refoulement, u' son coefficient de perte de charge linéaire, L' sa longueur et D' son diamètre.
Le coefficient u' varie généralement de 0,02 à 0,03 [REN 5][OUZ 224].
Compte tenu de (T18.5), la relation (T18.6) s'écrit :
(T18.8) pF(t) = patm + r g (zG - zF(t)) + (1/2) r (j8 - (S' / Si)2) (v(t))2 + r L' dv/dt
laquelle se dérive en :
(T18.8') d(pF)/dt = r g (S' / Si) v(t) + r (j8 - (S' / Si)2) v(t) dv/dt + r L' d2v/dt2
Compte tenu de (18.4) et (18.5), la relation (T18.2) se dérive en :
(T18.2') d(pF)/dt = - (pF7 volair7 / (volair(t))2) d(volair)/dt = - (pF7 volair7 / (volair(t))2) S' v(t)
En éliminant la quantité d(pF)/dt entre ces deux dernières relations, on trouve finalement l'équation générale du mouvement de l'eau dans la conduite de refoulement à tout instant (t) :
(T18.9) d2v/dt2 + M8 v(t) dv/dt + N8 v(t) = 0
dans laquelle :
dv/dt et d2v/dt2 sont respectivement les dérivées première et seconde de la vitesse v par papport au temps t
(T18.10) M8 = (1 / L')(j8 - (S' / Si)2)
(T18.11) N8 = (S' / L')( (g / Si) + (1/r)(pF7 volair7 / (volair(t))2) )
En pratique, les quantités (S' / Si)2 et (1 + f8)/ j8 sont petites devant 1 et la relation (T18.10) se simplifie en :
M8 # (u' / D') Signe[v(t)]
Compte tenu de (T17.2), la vitesse v(t) ne peut pas devenir négative, ce qui s'écrit :
(T18.12) v(t) > 0
Et l'expression de M8 se simplifie en :
(T18.10') M8 # u' / D'
l'unité de M8 étant en m-1.
Par ailleurs, le volume d'air comprimé (volair) variant très peu par rapport au volume d'air comprimé (volair7) en fin de phase 7, la relation (T18.11) se simplifie en :
N8 # (S' / L')( (g / Si) + (1/r)(pF7 / volair7) )
En pratique, la quantité [ r g (volair7 / Si) / pF7 ] étant petite devant 1, cette relation se simplifie encore en :
N8 # (S' / L')(1/r)(pF7 / volair7)
Compte tenu de (T18.3), cette dernière relation se simplifie finalement en :
(T18.11') N8 # B8 (S' / L')(1/r)(pF7)2
dans laquelle :
(T18.11'') B8 = 1/(volairatm patm)
pF7 est donné par la relation (T18.63),
l'unité de N8 est en s-2.
L'équation (T18.9) donnant la vitesse v(t) est une équation différentielle non linéaire du second ordre. En effectuant le changement de variable suivant :
(T18.13) w = (M8/N8) v
dont l'unité est en s,
alors cette équation se met sous la forme simple :
(T18.14) d2w/dt2 + N8 w (1 + dw/dt) = 0
laquelle s'intègre en :
(T18.15) f(dw/dt) = (1/2) N8 (C - w2)
où C est une constante dépendant des conditions particulières de la phase 8, et f(x) est une fonction de la variable x telle que :
(T18.16) f(x) = x - ln[ Valeur_absolue_de[1 + x] ]
Remarques :
La fonction f(x) s'annulant en x = 0 et x = -1,28 de part et d'autre de la valeur x = -1, la constante C ne peut pas être négative.
En pratique, l'accélération dv/dt ne subissant pas de discontinuité durant la phase 8, la variable dw/dt ne peut jamais atteindre la valeur -1 et l'on a de plus :
(T18.17) dw/dt > -1
Pour trouver w(t), il reste à intégrer l'équation (T18.15), ce qui sort du cadre de cette étude.
On retiendra seulement que la vitesse v(t), égale à (N8/M8) w(t), est une fonction d'abord croissante de t puis décroissante (voir Figure P3).
La courbe w(t) possède un maximum égal à :
(T18.18) w maxi = (C)1/2
Calcul de dv/dt(t=0) et dv/dt(t=t8)
L'utilisation de la relation (T17.2) dans la relation (T18.15) donne l'égalité suivante :
f((dw/dt)(t=0)) = f((dw/dt)(t=t8))
ce qui s'écrit, compte tenu de l'expression de PSI donnée en (T18.54) :
(T18.30) (dw/dt)(t=0) = (dw/dt)(t=t8) + PSI
(T18.31) (dw/dt)(t=t8) = -1 + ( PSI / (ePSI - 1) )
Remarques :
(T18.32) L'accélération (dw/dt)(t=0) est toujours comprise entre les valeurs PSI/2 et PSI selon que PSI est extrêmement petit ou extrêmement grand.
(T18.33) Compte tenu de (T18.30)(T18.32), on en déduit que :
(dw/dt)(t=0) + (dw/dt)(t=t8) = 2 (dw/dt)(t=0) - PSI > 0
(T18.34) ce qui indique que le courbe w(t) (et donc également la courbe v(t)) est plus pentue en t=0 qu'en t=t8 (voir Figure P3).
D'où finalement les expressions de dv/dt(t=t8) et dv/dt(t=0), compte tenu de (T18.13) :
(T18.30') (dv/dt)(t=0) = (N8/M8) (dw/dt)(t=0)
(T18.31') (dv/dt)(t=t8) = (N8/M8) (dw/dt)(t=t8)
Calcul de v8 et w7
En pratique et lorsque le fonctionnement du bélier est normal, la montée de pression de la cloche reste raisonnable (voir (T26.11 en Conclusion partielle). Dans ce cas, la courbe v(t) est très plate. La vitesse moyenne de l'eau dans la conduite de refoulement étant connue (T26.11.51), la vitesse v8 peut s'écrire :
(T18.40) v8 # v moyen
Par ailleurs, compte tenu de (T18.13)(T17.2), on trouve l'expression équivalente de w7 :
(T18.41) w7 # (M8/N8) (v moyen)
Remarque : La validité de l'approximation (T18.40) est à vérifier ultérieurement. Compte tenu de (T18.13)(T18.15)(T18.18), il suffira de comparer la vitesse moyenne (v moyen) avec la vitesse maximale (v maxi), cette dernière étant donnée par :
(T18.42) v maxi = (N8/M8) (w72 + (2/N8) f( (dw/dt)(t=0) ))1/2
Expression de vol8
Lorsque le fonctionnement du bélier est stabilisé (voir (T26.11 en Conclusion partielle), le volume d'eau refoulé dans la conduite de refoulement à chaque cycle est exactement égal au volume d'eau introduit dans la cloche pendant la même durée, ce qui s'écrit :
(T18.50) vol7 + vol8 = vol3*
avec vol3* donné par (T18.61).
En pratique, la durée t7 étant petite par rapport au temps de cycle, on peut écrire plus simplement :
(T18.51') vol8 # vol3*
Par ailleurs, le volume vol(t) véhiculé depuis le début de la phase 8 jusqu'au temps t s'écrit :
vol(t) = S' ∫t0[ v dt ]
ou encore, en utilisant la relation (T18.13) :
vol(t) = (S' / M8) ∫t0[ N8 w dt ]
Compte tenu de (T18.14), cette expression s'intègre en :
(T18.52) vol(t) = (S' / M8) ln[ (1 + (dw/dt)(t=0)) / (1 + (dw/dt)(t)) ]
d'où l'expression de vol8 :
(T18.53) vol8 = (S' / M8) PSI
(T18.54) PSI = ln[ (1 + (dw/dt)(t=0)) / (1 + (dw/dt)(t=t8)) ]
Remarque : La connaissance de vol3* permet donc de calculer facilement la quantité PSI utilisée par ailleurs.
Calcul de pF7
Presque toutes les formules du paragraphe "Phase 8" contiennent, de façon implicite ou explicite, la constante pF7 qu'il faut calculer en tenant compte de la montée de pression dans la cloche (voir (T26.11) en Conclusion partielle).
Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), le remplacement des grandeurs H et U donne, pour la condition (T13.10') et compte tenu de (T21.2), l'expression correcte du volume d'eau (vol3*) introduit dans la cloche à chaque cycle :
(T18.60) vol3* # (1/2) S L v02 / (g h U*)
Compte tenu de (T26.11.41), cette relation se simplifie alors en :
(T18.61) vol3* # A8 / (pF7 - patm - r g h)
(T18.61') A8 = (S L) (1/2) r v02
Compte tenu de (T18.8)(T18.10), l'expression de pF7 s'écrit alors :
(T18.63) pF7 = pF(t=0) = patm + r g H + r L' ( (1/2) M8 (v72) + (dv/dt)(t=0) )
ce qui est équivalent, compte tenu de (T18.13), à l'expression suivante :
(T18.63') pF7 = patm + r g H + r L' (N8/M8) X
(T18.64) X = (1/2) N8 w72 + (dw/dt)(t=0)
dans laquelle :
w7 et (dw/dt)(t=0) sont donnés respectivement par (T18.41) et (T18.32) ;
M8 et N8 sont donnés respectivement par (T18.10')(T18.11') ;
PSI, vol8 et vol3* sont donnés respectivement par (T18.53)(T18.51')(T18.61).
Simplification de pF7
En pratique, la quantité dw/dt(t=0) est souvent petite devant 1 (à vérifier ultérieurement). Compte tenu de (T18.32), cette quantité peut alors se simplifier en :
(T18.70) dw/dt(t=0) # PSI/2
Compte tenu de T18.53)(T18.51')(T18.41)(T26.11.51), la quantité w7 se simplifie également en :
(T18.71) w7 # PSI / (N8 tcycle)
Compte tenu de (T26.11.21), la relation (T18.63') donnant la pression pF7 se simplifie alors en :
(T18.75) E8 = B8 + F8 L' / (D'5)
avec :
(T18.76) E8 = (2/ A8) (Rr - h/H) (Rr - 1) / ( Rr + (patm/(r g H)) )2
(T18.77) F8 = (16/ (π2)) A8 u' / ( (tcycle2) g (H Rr - h)(patm + r g H Rr)2 )
A8 et B8 donnés respectivement par (T18.61') et (T18.11'')
Rr étant le ratio de montée de pression de la cloche, donné en (T26.11.21) et égal à : Rr = (pF7 - patm)/(r g H).
La relation (T18.75) donnant le ratio Rr, ou la pression pF7 équivalente, se résout numériquement par itérations successives des deux membres de la relation (T18.75). Si la quantité E8 est inférieure à B8, il n'y a pas de solution et il faut revoir le dimensionnement du dispositif de refoulement (voir Conclusion partielle).
Remarque : Compte tenu de l'expression (T18.75), la pression pF7 est alors d'autant plus petite que :
- le volume d'air de la cloche au démarrage du bélier (volairatm) est plus grand ;
- le diamètre D' est plus grand ;
- la hauteur de refoulement (H) est plus petite ;
- la longueur de refoulement (L') est plus petite.
La consolidation sur un cycle de l'ensemble des résultats précédents obtenus pour chaque phase i permet maintenant d'expliciter les équations de base (P1)(P5)(P6)(P7).
Nous allons découvrir que le modèle de fonctionnement du bélier hydraulique repose essentiellement sur les paramètres suivants :
- les caractéristiques de la conduite motrice (longueur L et section S) ;
- l'altitude du bélier (hauteur motrice h et hauteur de refoulement H) ;
- les caractéristiques du clapet de choc (coefficient de raideur K du joint et résistance F0 du clapet à sa fermeture) ;
- les dimensions du dispositif de refoulement (volume d'air volairatm de la cloche et diamètre D' de la conduite de refoulement).
D'autres paramètres, tels que la course totale (e0) du clapet de choc et la section droite (Sc) de l'obturateur de ce clapet, ont une moindre importance et sortent du périmètre de cette étude. Voir à ce sujet : (T10.0)(T11.3)(T12.0'')(T16.2) et [BER 98][CAR 76][OHA 14].
Notation : le sigle # signifie "peu différent de"
Lorsque le but recherché est d'optimiser la durée de vie du bélier (en particulier l'usure du clapet de choc), le temps de cycle est à étudier.
Compte tenu de (P5)(T11.1)(T11.3)(T12.1')(T12.5)(T13.2')(T13.11')(T14.1')(T14.2')(T15.7)(T15.8'')(T16.9)(T16.11'), on a :
tcycle = t1 + t2 + t3 + t4 + t5 + t6
avec :
t1 = (2 e0 / J)1/2
t2 # Z (&v / v1)( 1 + (1/2)(&v / v1) )
t3 # (L/a)(v1 / &v) - (1/2) Z (&v / v1)
t4 # 2 (L Z/a)1/2
t5 # 2 (1/g)(L/h)(-v4)
t6 # B - (1/g)(L/h) v5
v1 # v0
v4 # -&v (Z a/L)1/2
v5 # -v4
v6 = v0
&v = U h g/a
Z = (r/Y)(1/S)a
Pour B, selon que v0 est maintenu constant ou non autour de la valeur v0 opt (T26.0), on a :
B # (4/3)(1/g)(L/h) (v0 opt)
ou bien
B = (1/j)(L / vm) ln[ ( 1 + (v0 / vm) )/( 1 - (v0 / vm) ) ]
En remarquant que (&v / v0)2 est petit devant (&v / v0) en pratique (voir (T33.2)), il vient :
(-v4) # U g h/L (L Z/a)1/2
t2 + t3 # (L/a)(v1 / &v) + (1/2) Z (&v / v1) # (1/g)(L/h)(1/U) v0 + (1/2) g h U (Z/a)(1/ v0)
t5 + t6 # B + (1/g)(L/h)(-v4) # B + U (L Z/a)1/2
t5 + t6 + t4 # B + (U + 2) (L Z/a)1/2
d'où :
|
(T21.0) tcycle # t1 + B + (1/g)(L/h)(1/U) v0 + (1/2) g (r/Y)(1/S)(h U / v0) + (U + 2) (L (r/Y)(1/S))1/2 Le temps de cycle (tcycle) dépend donc essentiellement des caractéristiques de la conduite motrice (longueur L et section S), de l'altitude du bélier (hauteurs h et H) et des caractéristiques du clapet de choc (coefficient K = Y Sc2 du joint et force F0 = Q v02 du clapet). Après étude de l'influence de chacun de ces paramètres sur le temps de cycle (tcycle), on obtient que tcycle est une fonction : - croissante de la longueur L [BOR 95] et de la force F0 ; - décroissante de la section S et du coefficient K ; - d'abord décroissante de la hauteur h puis fortement croissante ; - d'abord décroissante de la hauteur H puis faiblement croissante [LAN 64 figure 25, 68]. Les Figures T1a à T3b illustrent l'influence de chacun de ces six paramètres sur tcycle. |
Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), la relation (T21.0) se simplifie en :
|
(T21.1) tcycle opt # t1 + (T opt) ((4/3) + (1/U)) (T21.2) T = (1/g) (L/h) v0 |
Cette dernière quantité (T), assimilable à un temps, est une caractéristique fondamentale du bélier, que nous retrouverons par la suite.
Application numérique : si h = 3 m ; H = 30 m ; L = 20 m ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
T opt = 0,68 s
tcycle opt # 1,1 s
Lorsque le but recherché est de refouler la plus grande quantité d'eau possible [REN 36], le débit refoulé en moyenne sur un ou plusieurs cycles est à étudier.
Compte tenu de (T11.1)(T12.1')(T13.2')(T13.10), on a :
vol3 # (1/2) S v1 ( (L/a)(v1 / &v) - Z (&v / v1) )
v1 # v0
&v = U h g/a
Z = (r/Y)(1/S)a
Après remplacements, il vient :
|
(T22.0) vol3 # (1/2) S (1/g)(L/h)(1/U)(v02) - (1/2) g h U (r/Y) (T22.1) qF = vol3 / tcycle avec vol3 donné par (T22.0) et tcycle par (T21.0). Le débit moyen refoulé (qF) dépend donc essentiellement des caractéristiques de la conduite motrice (longueur L et section S), de l'altitude du bélier (hauteurs h et H) et des caractéristiques du clapet de choc (coefficient K = Y Sc2 du joint et force F0 = Q v02 du clapet). Après étude de l'influence de chacun de ces paramètres sur le débit (qF), on obtient que qF est une fonction : - croissante de la section S, du coefficient K et de la hauteur h ; - décroissante de la hauteur H [LAN 61 figure 22, 68][OBR 8 figure 9][BOR 95] ; - d'abord croissante de la longueur L puis décroissante ; - d'abord croissante de la force F0 puis décroissante. Les Figures T1a à T3b illustrent l'influence de chacun de ces six paramètres sur qF. |
Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), on a de plus les particularités suivantes :
a) La courbe qF fonction de L possède un maximum qui est atteint pour un rapport particulier (x part) vérifiant la relation :
(T22.2) ((j part)2) (D/u) v0 t1 (1/(L part)2) = X part
avec :
(T22.2') X = (x2)/( 1 - x2 ) - (1/2) (x) ln[ (1 + x)/(1 - x)) ]
x part = v0 / (vm part)
vm part = (2 (1/(j part)) g h)1/2
j part = 1 + f + fh + u (L part)/D
ce qui donne pour solution approchée :
(T22.2'') x part # (A + (B)1/2)1/2
(T22.2''') qF maxi # (1/2) S v0 (1/U) (1 - (x part)2)
avec :
A = (1/2)(1/g)(1/h)(1 + f + fh)(v02)
B = (5/4) (u/D) v0 t1
A et B étant supposés petits devant 1.
Application numérique : si h = 3 m ; D = 0,1 m ; u = 0,02 ; f = 3 ; v0 = 1 m/s ; t1 = 0,1 s ; on obtient :
A = 0,068
B = 0,025
x part # 0,48
vm part # 2,1 m/s
j part # 13,6
L part # 47 m
qF maxi # 0,4 l/s
Remarque : La courbe qF en fonction de L est très plate autour de la longueur particulière (L part), comme le montre également la Figure T1a. La longueur L influe donc très peu sur le débit moyen refoulé, en-dehors des longueurs extrêmes (cas : vol3 = 0 et cas : v0 = vm). Diminuer la longueur L fait battre le bélier plus vite (voir courbe tcycle en fonction de L) mais diminue dans la même proportion le volume d'eau refoulé par cycle. Ce cas théorique ne se produit cependant jamais en fonctionnement optimal lorsque la vitesse v0 est modifiée en même temps que la longueur L (via le réglage optimal de la force F0 (T26.0)).
b) La courbe qF fonction de F0 possède un maximum qui est atteint pour un rapport particulier (x part) vérifiant les relations :
(T22.3) x part # ((G + 1,28)/(G + 2))1/2
(T22.3') qF maxi # S vm (1/U) (x part) (1 - (x part)2)
avec :
x part = (v0 part) / vm
(T22.4) G = j vm t1 / L
Cette quantité (G), sans unité, est une caractéristique fondamentale du bélier ([BER 88][CAR 75] avec "K" auteurs = G (1/j)1/2) que nous retrouverons par la suite.
Pour des valeurs courantes de G en dessous de la valeur 2, le maximum de qF relativement à F0 est atteint pour x part # 0,85
Application numérique : si h = 3 m ; L = 20 m ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3) :
vm # 2 m/s
G # 0,15
x part # 0,82
v0 part # 1,6 m/s
F0 part = Q (v0 part)2
qF maxi # 0,6 l/s
De façon générale, pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), la relation (T22.1) se simplifie en :
|
(T22.5) qF opt # (1/2) S (v0 opt) b / (1 + b + c) |
avec :
b = (3/4)(1/U)
c = (3/4)(t1 / T opt)
Si, en plus, la quantité c est petite devant 1, alors on obtient finalement :
(T22.5') qF opt # (3/8) S (v0 opt) / (U + (3/4))
Application numérique : si h = 3 m ; H = 30 m ; L = 20 m ; S = 0,01 m2 ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
b = 0,083
c = 0,11
qF opt # 0,35 l/s
Lorsque le but recherché est de comparer la performance de deux béliers ou lorsque l'eau de source n'est pas gratuite, le rendement global est à étudier.
Compte tenu de (T11.2)(T12.1')(T13.2')(T14.1')(T15.7)(T16.9)(T16.10'), on a :
vol1 # S v0 t1
vol6 # A - (1/2) S (1/g)(L/h)(v52)
v4 # -&v (Z a/L)1/2
v5 # -v4
v6 = v0
&v = U h g/a
Z = (r/Y)(1/S)a
Pour A, selon que v0 est maintenu constant ou non autour de la valeur v0 opt (T26.0), on a :
A # (2/3)(1/g)(L/h) S (v0 opt)2
ou bien
A = (1/j) S L ln[ 1/(1 - (v0 / vm)2) ]
Après remplacements, il vient :
(-v4) # g U (h/L) (L Z/a)1/2
(T23.0) vol1 + vol6 # S v0 t1 + A - (1/2) g h (r/Y)(U2)
d'où, compte tenu de (P5)(T13.4)(T22.0)(T22.1) :
|
(T23.1) Rg # (qF / qE) U # ( (1/2) S (1/g)(L/h)(v02) - (1/2) g (r/Y) h (U2) ) / (vol1 + vol6) avec (vol1 + vol6) donné par (T23.0). Le rendement global (Rg) dépend donc essentiellement des caractéristiques de la conduite motrice (longueur L et section S), de l'altitude du bélier (hauteurs h et H) et des caractéristiques du clapet de choc (coefficient K = Y Sc2 du joint et force F0 = Q v02 du clapet). Après étude de l'influence de chacun de ces paramètres sur le rendement global (Rg), on obtient que Rg est une fonction : - croissante de la section S et du coefficient K ; - d'abord croissante de la longueur L puis décroissante ; - d'abord croissante de la hauteur h puis fortement décroissante ; - d'abord croissante de la hauteur H [REN 38] puis faiblement décroissante [LAN 47 figure 14][OBR 8 figure 9][NAV 347] ; - d'abord croissante de la force F0 puis décroissante [BER 93 figure 38, 91, avec K BERGERON # 0,01 et u L/D = u' L/D # 1]. Les Figures T1a à T3b illustrent l'influence de chacun de ces six paramètres sur Rg. |
Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), on a de plus les particularités suivantes :
a) La courbe Rg fonction de L possède un maximum qui est atteint pour un rapport particulier (x part) vérifiant la relation :
(T23.2) x part # (A + ((3/2) B)1/2)1/2
avec A et B donnés en (T22.2'''),
A et B étant supposés petits devant 1.
Application numérique : si h = 3 m ; D = 0,1 m ; u = 0,02 ; f = 3 ; v0 = 1 m/s ; t1 = 0,1 s ; on obtient :
x part # 0,51
Rg maxi # 0,76
b) La courbe Rg fonction de h possède un maximum qui est atteint pour un rapport particulier (x part) vérifiant les relations :
(T23.3) x part # ((G')/(G' + 1))1/4
(T23.3') Rg maxi # 1 - (x part)2
avec :
G' = j v0 t1 / L
x part = v0 / (vm part)
vm part = (2 (1/j) g (h part))1/2
Application numérique : si L = 20 m ; j = 15 ; v0 = 1 m/s ; t1 = 0,1 s ; on obtient :
G' = 0,075
x part # 0,51
h part # 2,9 m
Rg maxi # 0,74
c) La courbe Rg fonction de H possède un maximum qui est atteint pour une hauteur H particulière (H part).
En se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), et lorsque la quantité (t1 / T opt) est petite devant 1, H part vérifie les relations :
(T23.4) H part = h ( 1 + (2 A S (K / Sc2)(1/r)(1/L) (T opt)2)1/3)
(T23.4') A = (1/4) fr (1/g) (1/h) (v0 opt)2
(T23.4'') Rg maxi # (3/4)(1 - (A/U))
Application numérique : si h = 3 m ; L = 20 m ; S = 0,01 m2 ; j = 15 ; Sc # S ; K = 50 106 N/m ; t1 = 0,1 s ; fr = 3 ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
T opt = 0,68 s
t1 / T opt = 0,15
H part # 57 m
Rg maxi # 0,75
d) La courbe Rg fonction de F0 possède un maximum qui est atteint pour un rapport particulier (x part) vérifiant les relations :
(T23.5) x part # (G / (G + 3))1/4
avec :
x part = (v0 part) / vm
et G donné par la relation (T22.4).
Pour des valeurs courantes de G situées entre les valeurs 0,1 et 1, le maximum de Rg relativement à F0 est atteint pour x part # 0,50
A noter qu'on améliore toujours ce maximum en rendant plus petite la quantité G [BER 96][CAR 75].
Application numérique : si h = 3 m ; L = 20 m ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3) :
vm # 2 m/s
G # 0,15
x part # 0,47
v0 part # 0,9 m/s
F0 part = Q (v0 part)2
Rg maxi # 0,69
De façon générale, pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), la relation (T23.1) se simplifie en :
|
(T23.6) Rg opt # (3/4) / ( 1 + (3/2)(t1 / T opt) ) |
Remarque : Le rendement global du bélier ne peut donc pas dépasser la valeur 3/4 (pour t1 proche de zéro seconde), avec une valeur optimale de 2/3 (pour des valeurs usuelles de t1) [BOL-LEB 147].
Application numérique : si h = 3 m ; L = 20 m ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
t1 / T opt = 0,15
Rg opt # 0,61
Compte tenu de (T23.0)(T21.1)(T22.5'), pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), les équations (P5) et (P2) se simplifient respectivement en :
|
(T24.1) qE opt # (1/2) S (v0 opt) (1 + 2 c) / (1 + b + c) (T24.2) qB opt # (1/2) S (v0 opt) (1 + b + 2 c) / (1 + b + c) |
avec :
b = (3/4)(1/U)
c = (3/4)(t1 / T opt)
Si, en plus, la quantité c est petite devant 1, alors on obtient finalement :
(T24.1') qE opt # (1/2) S (v0 opt) U / (U + (3/4))
(T24.2') qB opt # (1/2) S (v0 opt)
Application numérique : si h = 3 m ; L = 20 m ; S = 0,01 m2 ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
b = 0,083
c = 0,11
qE opt # 5,1 l/s
qB opt # 5,5 l/s
La puissance utile (Pu) pour monter l'eau d'une hauteur (H - h) s'exprime par la relation [BER 89] :
(T25.1) Pu = r g (H - h) qF = r g h U qF
Compte tenu de (T22.5'), pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T25.0), et pour une quantité c petite devant 1, cette relation s'écrit :
|
(T25.2) Pu opt # (3/8) r g S (v0 opt) h U/ (U + (3/4)) |
Application numérique : si h = 3 m ; H = 30 m ; L = 20 m ; S = 0,01 m2 ; j = 15 ; t1 = 0,1 s ; on obtient, compte tenu de (T16.3)(T21.2) :
v0 opt = 1 m/s
c = 0,11
Pu opt # 100 W
|
Les Figures T1a à T3b illustrent l'influence de chacun des six paramètres essentiels (L, S, K = Y Sc2, h, H, F0 = Q v02) sur le trio de caractéristiques utile à connaître (tcycle, qF, Rg). Il faut retenir que : - Chacun de ces paramètres influe relativement peu sur le temps de cycle (tcycle), dans la mesure où l'on s'éloigne des temps de cycle extrêmes (cas : v0 = vm et cas : h = H). En pratique, selon l'installation et la taille du bélier, tcycle varie de 0,7 s à 4 s [REN 30][ANO 225]. - L'augmentation de la section (S) de la conduite motrice ou de la raideur du joint du clapet de choc (coefficient K) donne un rendement global (Rg) et un débit moyen refoulé (qF) plus grands. - L'augmentation de la longueur (L) de la conduite motrice donne d'abord un rendement global et un débit moyen refoulé plus grands, et dégrade ensuite ces deux caractéristiques. - L'augmentation de la hauteur motrice (h) du bélier donne d'abord un rendement global et un débit moyen refoulé plus grands, et dégrade ensuite le rendement global. - L'augmentation de la hauteur de refoulement (H) du bélier donne d'abord un rendement global plus grand et un débit moyen refoulé plus petit, et dégrade ensuite ces deux caractéristiques. - L'augmentation de la résistance (F0) du clapet de choc à sa fermeture donne d'abord un rendement global et un débit moyen refoulé plus grands, et dégrade ensuite ces deux caractéristiques. |
Pour avoir un fonctionnement optimal, le bélier hydraulique doit donc posséder :
Ce rapport optimal est l'un des deux réglages (avec la course e0 du clapet) à effectuer impérativement sur le bélier avant sa mise en service. Nous noterons par la suite :
|
(T26.0) x opt = (v0 opt) / vm # 1/2 Cependant, dans certains cas de fonctionnement, notamment pour faire battre le bélier moins vite et allonger sa durée de vie, ou afin de pouvoir refouler l'eau le plus haut possible, on peut choisir : x opt # 3/4 voire 4/5 sous réserve d'avoir une performance moindre pour le bélier. |
Remarque : Les auteurs [BER][REN][CAR] ont différentes approches sur ce sujet (voir Comparaison avec les abaques des fabricants).
L'atteinte de cet optimum nécessite, compte tenu de la relation générale donnée en (T10.0), un clapet de choc réglé avec la résistance (F0) optimale suivante :
(T26.0'') F0 opt = Fm (v0 opt / vm)2 # (1/4) Q vm2
En pratique, trois technologies différentes se présentent :
Cas 1 : Clapet de choc d'axe vertical (exemple : clapet à piston ou soupape) et F0 réalisée par ajout d'un poids modulable
Dans ce cas, si (Mm) désigne le supplément de masse juste nécessaire pour équilibrer le clapet de choc (de masse M_clapet) en régime permanent, alors la masse optimale (M opt) à rajouter vaut :
(T26.0''') M opt + M_clapet # (1/4) (Mm + M_clapet)
Le réglage consiste alors à bien mesurer la masse totale (Mm + M_clapet) puis à alléger le tout en enlevant les trois-quarts de cette masse totale.
Application numérique : si M_clapet = 360 g et Mm = 1640 g ; on doit avoir : M opt # 120 g
Remarque : Cette solution a l'avantage d'une mise en oeuvre simple. En revanche, l'alourdissement du clapet de choc diminue son accélération (J) et donc augmente sa durée (t1) de fermeture (voir (T11.3)), ce qui dégrade indirectement le rendement global (Rg) du bélier et le débit moyen refoulé (qF) (voir (T23.6) et (T22.5)). Le réglage nécessite par ailleurs un calcul théorique basé sur la connaissance de M_clapet.
Cas 2 : Clapet de choc d'axe horizontal (exemple : clapet à piston, soupape, battant, disque) et F0 réalisée par un ressort de raideur (K) et de longueur à vide (l vide)
Dans ce cas, si (lm) désigne la longueur du ressort juste nécessaire pour équilibrer le clapet de choc en régime permanent, compte tenu de la relation générale : F ressort = K (l vide - l), alors la longueur optimale (l opt) vérifie la relation :
(T26.0'''') l vide - l opt # (1/4) (l vide - lm)
ou encore : l opt - lm # (3/4) (l vide - lm)
Le réglage consiste alors à bien mesurer la différence de longueur (l vide - lm) puis à détendre le ressort d'une longueur égale aux trois-quarts de cette différence.
Application numérique : si l vide - lm = 4 cm ; on doit avoir : l opt - lm # 3 cm
Remarque : Cette solution a l'avantage d'un réglage indépendant de la durée de fermeture (t1) et proportionnel à l'extension (l vide - lm) en régime permanent. En revanche, elle est complexe à mettre en oeuvre (avec ressort interne et dispositif de compression ou traction du ressort).
Cas 3 : Clapet de choc d'axe horizontal (exemple : clapet à battant) et F0 réalisée par un contrepoids externe modulable (situé en bout d'une tige traversante solidaire du battant)
Dans ce cas, un premier réglage permet d'assurer l'équilibre à vide de l'ensemble battant - tige traversante, en position ouverte optimale du battant, par ajout de poids de tarage côté battant ou côté extrémité de tige. Ensuite seulement, on ajoute en bout de tige traversante la masse optimale (M opt).
Si (Mm) désigne la masse juste nécessaire pour équilibrer le clapet de choc en régime permanent, alors la masse optimale (M opt) à rajouter vaut :
(T26.0''''') M opt # (1/4) Mm
Le réglage consiste alors à bien mesurer la masse (Mm) puis à alléger le tout en enlevant les trois-quarts de cette masse.
Application numérique : si Mm = 1640 g ; on doit avoir : M opt # 410 g
Remarque : Cette solution a l'avantage d'une mise en oeuvre simple, sans calcul théorique, et avec un réglage proportionnel à la masse (Mm) en régime permanent. En revanche, elle a l'inconvénient du cas 1 (alourdissement du clapet), avec une robustesse moindre en durée de vie (usure de l'axe du battant et fatigue par flexion alternée de la tige traversante).
Cette longueur (L) vérifiant simultanément les relations (T22.2)(T26.0) est idéalement la solution numérique (L opt) de l'expression suivante :
(T26.6') (1 + f + fh) + (u/D) (L opt) = ( A-2/3 ) (L opt)4/3
avec :
A = (D/u) t1 ( (x opt) / (X opt) ) (2 g h)1/2
et (x opt) donné par (T26.0),
et (X opt) donné par (T22.2') après remplacement de x par xopt.
Application numérique : si h = 3 m ; H = 30 m ; D = 0,1 m ; u = 0,02 ; f = 3 ; t1 = 0,1 s ; on obtient :
x opt # 1/2
X opt = 0,059
A = 32,5
L opt # 33 m
v0 opt # 1,2 m/s
t1 / (T opt) # 0,07
1/U # 0,11
qF maxi # (3/8) S (v0 opt) (1/U) # 0,4 l/s
En pratique, les auteurs [REN][CAR][SCH][COD][ANO] présentent une fourchette (basse et haute) pour la longueur L (voir Comparaison avec les abaques des fabricants). La longueur L n'étant pas déterminante dans l'optimisation d'un bélier (voir Remarque du (T22.2)), on peut prendre arbitrairement :
|
(T26.6'') L # n h |
avec en général : n = 10
(T26.6''') Remarque : Dans certaines installations, il peut être nécessaire d'augmenter ou de réduire artificiellement L lorsque la distance entre la source et le bélier est inappropriée.
- Pour augmenter L, il suffit d'enrouler en hélice la conduite motrice autour d'un cylindre vertical de grand diamètre [REN 50].
- Pour réduire L, et en même temps les pertes de charge linéaire dans la conduite motrice, il suffit de placer à la longueur L souhaitée un bassin intermédiaire ou une cheminée, ce qui augmente artificiellement la pente (h/L) de la conduite motrice [REN 51, 63][ANO 227].
A ne pas confondre avec la "cheminée d'équilibre" dont la fonction anti-bélier permet de protéger des installations ou des machines par absorption rapide d'une onde de choc accidentelle, alors que la cheminée envisagée ici doit continuer à assurer la fonction de guide d'onde le plus longtemps possible.
La cheminée ne doit pas être placée trop près du bélier ou de la source, sous peine de provoquer des battements doubles, l'onde de choc provenant de la cheminée se trouvant contrariée par l'onde de choc provenant de la source. En pratique, on place la cheminée à peu près à mi-chemin de la longueur L.
On remarque en effet que le débit moyen refoulé (qF) et le rendement global (Rg) sont d'autant plus grands que la durée (t1) de fermeture du clapet de choc est plus petite (voir (T22.5) et (T23.6)). Compte tenu de (T11.3), le clapet de choc doit donc posséder une grande accélération (J) et en conséquence une petite masse [BOR 99][NAV 346].
Remarque : cette condition ne peut pas être remplie si on fait le choix, par ailleurs, d'un réglage de la résistance (F0) du clapet de choc à sa fermeture par ajout de poids modulables (voir (T26.0'')).
Bien que cette recommandation sorte du cadre de cette étude, on peut remarquer toutefois que cette course est un compromis entre :
- une course pas excessivement petite pour ne pas trop augmenter la perte de charge singulière (f) de ce clapet (T16.2) et dégrader la vitesse de l'eau en régime permanent (vm) (voir T16.3), la vitesse optimale de l'eau (v0 opt) (voir T26.0) et le débit moyen refoulé (qF) (voir T22.5).
- une course pas excessivement grande pour ne pas trop augmenter la durée (t1) de fermeture du clapet de choc (T11.3) et dégrader le débit moyen refoulé (qF) (voir T22.5).
Remarque : Certains fabricants de béliers préconisent d'ajuster le débit moyen absorbé (qB) en modifiant la course totale (e0) du clapet de choc. Cela reste valable seulement pour de petits ajustements et, en pratique, nous conseillons plutôt d'utiliser la vanne d'isolation et de réglage du débit située sur la conduite motrice, permettant un réglage fin et manoeuvrable facilement (voir Figure C1 au chapitre Pratique).
Il convient en effet, de profiter pleinement de l'ensemble des forces de pression et de quantité de mouvement qu'exerce l'eau sur le clapet de choc en position ouverte (voir Début du cycle). Et il est toujours gagnant de maximiser la force (hydrodynamique) de quantité de mouvement s'exerçant sur le chapeau du clapet. C'est le cas de certains béliers ([SCH][COD][WAL][ANO 224] et béliers Samain [BER 101], E. Lacroix [BER 102], Ledoux [REN 23]), lesquels respectent cette condition de perpendicularité.
Bien que cette recommandation sorte du cadre de cette étude, on peut remarquer toutefois que cette section est un compromis entre :
- une section pas excessivement grande pour ne pas trop augmenter la perte de charge singulière (f) de ce clapet (T16.2) et dégrader la vitesse de l'eau en régime permanent (vm) (voir T16.3), la vitesse optimale de l'eau (v0 opt) (voir T26.0) et le débit moyen refoulé (qF) (voir T22.5).
- une section pas excessivement petite pour ne pas trop diminuer la force de l'eau sur le clapet (voir T10.1) et avoir une fermeture trop lente du clapet qui donnerait un coup de bélier médiocre et dégraderait le débit moyen refoulé (qF).
En pratique, on veillera à avoir une section droite de passage du flux d'eau autour de l'obturateur approximativement égale au tiers de la section droite du flux d'eau amont dans le clapet.
Le dispositif complet de refoulement du bélier (volume d'air de la cloche et dimensions de la conduite de refoulement) doit répondre à trois exigences :
(T26.11.1) 1) Protéger l'installation des coups de bélier éventuels
L'absence totale d'air dans la cloche est dangereuse, l'eau de la conduite de refoulement opposant une inertie qui permettrait à un coup de bélier de s'établir dans cette conduite et de l'endommager [BER 101]. Souvent, dans ce cas, le clapet de refoulement perd son étanchéité, le bélier continue cependant de battre mais sans refouler d'eau et à une cadence anormalement rapide [REN 66].
Il convient donc de dimensionner toute l'installation (conduite motrice, corps du bélier, cloche à air) afin qu'elle résiste à la pression effective maximale pouvant survenir dans la cloche (voir T37.1).
(T26.11.2) 2) Interdire une montée excessive de pression dans la cloche
Si le dispositif de refoulement est bien dimensionné, le volume d'eau (vol3*) introduit dans la cloche à chaque cycle durant la phase 3 est intégralement chassé dans cette conduite durant les phases suivantes 8 puis 7.
Dans le cas contraire (volume d'air insuffisant, conduite de refoulement trop étroite ou partiellement bouchée, etc.), le volume d'air comprimé dans la cloche se réduit en deçà de la normale et la pression de l'air dans la cloche, devenant supérieure à la normale [CHA 14], contribue alors à chasser l'excédent d'eau pendant le ou les cycles suivants. Ainsi, durant les premiers cycles du démarrage du bélier, la cloche monte en pression et devient capable, seulement ensuite, de refouler intégralement le volume d'eau introduit dans la cloche à chaque cycle ; la cloche garde ensuite cette pression en fin de chaque phase 7 de refoulement. Ce fonctionnement anormal revient à augmenter artificiellement la hauteur de refoulement H, ce qui dégrade sensiblement le rendement global (Rg) et le débit moyen refoulé (qF) du bélier (voir Figure T2a).
En outre, dans le cas limite où la pression (pF7) deviendrait excessive, l'onde de choc dans la conduite motrice n'est plus suffisante pour ouvrir le clapet de refoulement ; le bélier continue alors de fonctionner mais ne pompe plus d'eau vers le réservoir supérieur.
Afin d'interdire toute montée excessive de pression dans la cloche, on définit un ratio (Rr > 1) de montée de pression de la cloche :
(T26.11.21) Rr = (pF7 - patm)/(r g H)
En pratique, ce ratio ne doit jamais dépasser raisonnablement la valeur 1,1.
Le ratio Rr étant maintenant fixé, ainsi que la longueur de refoulement (L') souvent imposée par le terrain, il reste à trouver la valeur optimale du diamètre de refoulement (D') et du volume d'air au démarrage du bélier (volairatm). L'expression générale (T18.75) fournit dans un premier temps la valeur minimale de volairatm (en prenant D' = ∞) et la valeur minimale de D' (en prenant volairatm = ∞), ce qui s'écrit :
(T26.11.22) volairatm mini = 1 / (patm E8)
(T26.11.23) D' mini = (F8 L' / E8)1/5
avec E8 et F8 donnés respectivement par (T18.76) et (T18.77).
Voir calcul appliqué au chapitre Pratique - Calcul.
Remarque : la relation (T18.75) s'écrit alors plus simplement :
(T26.11.24) 1 = ((volairatm mini)/volairatm) + ((D' mini)/D')5
(T26.11.3) 3) Permettre l'ajout d'un volume d'air supplémentaire (réhausseur)
En pratique, il faut pouvoir ajuster le couple (volairatm, D') de façon optimale, notamment en rajoutant, si nécessaire, un réhausseur entre la cloche et la base du bélier. Cette astuce augmente le volume d'air (volairatm) et permet de compenser un diamètre D' trop petit et souvent non modifiable (cas d'une installation existante).
Pour cela, on définit un ratio (Rc) de sensibilité de la cloche, égal à :
(T26.11.31) Rc = -(d(D')/d(volairatm)) (volairatm/D')
En pratique, on se fixe la valeur Rc = 1/2 pour avoir une souplesse confortable dans l'ajustement mutuel de volairatm et de D'. Compte tenu de (T18.75), on obtient finalement la valeur optimale de volairatm et D' sous la forme :
|
(T26.11.32) volairatm opt = (volairatm mini) (1 + (1/5)(1/Rc)) (T26.11.33) D' opt = (D' mini) (1 + 5 Rc)1/5 |
avec (volairatm mini) et (D' mini) donnés respectivement par (T26.11.22) et (T26.11.23).
Voir calcul appliqué au chapitre Pratique - Calcul.
(T26.11.4) 4) Cas du dispositif de refoulement mal dimensionné
Si les considérations précédentes ne permettent pas de bien dimensionner le dispositif de refoulement (ce qui peut être le cas d'une installation existante et non modifiable), il faut se résigner à subir la montée excessive de pression de la cloche et à accepter une dégradation du rendement global (Rg) et du débit moyen refoulé (qF) du bélier.
Il convient alors de remplacer, dans toute cette étude sur le bélier (hormis les relations de base (P1)(T18.63)(T26.11.21)(T33.1'')), l'expression des grandeurs H et U par les expressions H* et U* suivantes :
(T26.11.41) H* = (pF7 - patm)(1/r)(1/g) = H Rr
U* = H* / h - 1
pF7 étant donné par la relation (T18.63') dans laquelle w7 est solution de l'équation (T18.15).
La hauteur H* correspond à une hauteur artificielle de refoulement qui prend en compte cette montée de pression dans la cloche. H* peut être très supérieure à la hauteur de refoulement (H) et peut donc modifier fortement l'ensemble des calculs et résultats de cette étude.
(T26.11.5) 5) Remarque sur la vitesse d'écoulement de l'eau
L'eau s'écoule dans la conduite de refoulement en continu ou par soubresauts selon que la hauteur de refoulement est plus ou moins grande ; les béliers qui n'ont qu'une dizaine de mètres d'ascension montent toujours leur eau par soubresauts, avec cessation d'écoulement entre chaque coup [CHA 18].
La vitesse moyenne de l'eau dans la conduite de refoulement est donnée par la relation :
(T26.11.51) v moyen = (1 / tcycle)(vol3* / S')
Compte tenu des relations (T26.11.21)(T18.61)(T18.61'), cette vitesse moyenne s'écrit alors :
v moyen # (1/2)(S L) v02 / (tcycle S' g (H Rr - h))
Application numérique : si h = 3 m ; H = 30 m ; L = 20 m ; S = 0,01 m2 ; v0 = 1 m/s ; D' = 0,03 m ; Rr = 1,1 ; tcycle = 1,1 s ; on obtient :
v moyen = 0,44 m/s
Mais l'ensemble de ces résultats de ce chapitre Conclusion n'est que partiel car :
- d'autres conditions interviennent pour assurer le bon fonctionnement du bélier : son lancement, son fonctionnement normal sur un cycle et son fonctionnement régulier dans le temps (voir Conditions de fonctionnement) ;
- d'autres résultats pratiques apparaissent lorsqu'on cherche à calculer un bélier (voir Pratique - Calcul) ;
Une synthèse sera donnée en final (voir Pratique - Conclusion générale).
Les conditions de fonctionnement théoriques d'un bélier hydraulique sont les suivantes :
Le bélier ne doit pas s'arrêter par présence d'obstacles ou par manque d'eau dans la conduite motrice. Pour cela :
(T31.1) 1- L'eau doit être propre, sans corps étrangers flottants (herbes, feuilles...) ou immergés (solides, petits animaux...). Solution : utiliser un filtre adapté en sortie B de collecteur [REN 63, 64]. Pour les corps immergés, le filtre doit empêcher le passage dans la conduite motrice des petits animaux (poisson, grenouille...), le colmatage de la surface des trous du filtre par les solides & boues et le coincement des solides dans l'épaisseur des trous. Solution pour avoir un système quasi-autonettoyant : préférer les filtres à fentes continues aux filtres classiques à petites mailles.
(T31.2) 2- L'eau ne doit pas contenir de poches d'air, dont l'élasticité dégraderait l'onde de choc dans la conduite motrice (avec réduction du débit refoulé) et limiterait également le recul de l'eau dans la conduite motrice (avec risque d'arrêt du bélier lorsque le clapet de choc ne s'ouvre plus) [CHA 21]. Solution : s'assurer que la conduite motrice est bien étanche et ne possède aucun tronçon à courbure négative [REN 63][SCH 3][COD][CHA 24][ANO 234].
(T31.3) 3- L'eau ne doit pas geler. Solution : mettre hors gel la conduite motrice, par exemple en creusant une tranchée à bonne profondeur (minimum 50 cm) remplie partiellement de sable [OHA 49].
(T31.4) 4- L'eau doit être disponible en permanence, hiver comme été [REN 55, 66]. Solutions : calculer le bélier de façon à avoir un débit moyen absorbé (qB) tel que :
|
(T31.5) qB < k (qA mini) |
et ajouter une vanne de réglage sur la conduite motrice [REN 63][ANO 234] pour ajuster les petits écarts éventuels par rapport au débit nominal (qB).
qB étant donné par (T24.2) lorsqu'on se place autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0),
(qA mini) étant le débit source minimal (obtenu en général en fin de l'été),
le ratio k correspondant au quota maximal d'eau prélevée par le bélier par rapport à la source. Pour les petits débits source, le ratio k doit être soigneusement choisi sous peine d'arrêt du bélier par manque d'eau, et on prend en général par sécurité : k = 0,8. Pour les débits plus importants, le ratio k est plafonné volontairement (exemples : 0,1 ou 0,01) pour réduire le coût de l'installation. Voir également [COD].
Si, en plus, les quantités (t1 / T opt) et (1/U) sont petites devant 1, alors la relation (T31.5) se simplifie en :
(T31.5') k (qA mini) > (1/2) S (v0 opt)
Compte tenu de (T26.0)(T16.3), on obtient finalement :
(T31.5'') j opt > (1/8) g h (S2) / ( k (qA mini) )2
Remarque : Les courbes de fonctionnement de béliers de série rendent compte de cette relation (voir Comparaison avec les abaques des fabricants)).
Remarque : Dans le cas d'une source munie d'un déversoir à seuil épais (barrage établi en travers d'un canal), on peut estimer simplement le débit source (qA) en utilisant la formule suivante [OUZ 114] :
(T31.6) qA # b y (g y)1/2
dans laquelle b est la largeur du canal et y la hauteur d'eau juste au niveau du seuil du déversoir.
Application numérique : pour toute tranche b = 0,1 m on a :
qA # 19 l/mn pour y = 0,01 m
qA # 53 l/mn pour y = 0,02 m
qA # 98 l/mn pour y = 0,03 m
qA # 150 l/mn pour y = 0,04 m
qA # 210 l/mn pour y = 0,05 m
En fin de phase 1, le clapet de choc doit impérativement se fermer, sous peine d'interrompre le cycle de fonctionnement du bélier. Pour cela :
- Le clapet de refoulement doit déjà être fermé, ce qui correspond à un écart positif de pression de part et d'autre de ce clapet, soit :
(T32.1) r g (H - h) > 0
ou encore :
(T32.2) h/H < 1
Cette condition est toujours vérifiée lorsque (T35.3) l'est.
- La vitesse de l'eau dans la conduite motrice ne doit jamais atteindre le régime permanent (voir Phase 6), ce qui correspond à la condition :
(T32.3) v1 < vm
Compte tenu de (T11.1), cela s'écrit [REN 49] :
|
(T32.4) v0 / vm < 1 |
Cette condition est toujours vérifiée lorsque (T26.0) l'est.
En fin de phase 2, le clapet de refoulement doit impérativement s'ouvrir, sous peine d'interrompre le cycle de fonctionnement du bélier. Pour cela, on doit avoir [LAN 20] (voir Phase 3) :
(T33.1) (&p)1 > r g (H - h) + (F2 / s')
où F2 est la résistance du clapet de refoulement à son ouverture en fin de phase 2,
et s' est la section droite de l'obturateur du clapet de refoulement.
(T33.0) On suppose que le clapet de refoulement est bien réglé de façon que la pression mécanique (F2 / s') soit négligeable par rapport à la différence de pression statique égale à : r g (H - h). Pour cela, il suffit que le poids total du clapet de refoulement (avec lest éventuel) ne soit pas excessif et que le ressort de compression ait une raideur non excessive ainsi qu'une longueur sous charge non trop réduite. Sous ces conditions, compte tenu de (T11.1)(T13.0)(T13.1), la condition théorique d'ouverture du clapet de refoulement est équivalente à la condition suivante :
(T33.1a) v0 > (g/a) h U
avec U donné par (T13.4').
Remarque : compte tenu de (T13.2'), la condition (T33.1a) s'écrit également :
(T33.2) v0 > &v
En situation limite (v0 # &v), le volume d'eau refoulé par cycle (vol3) devient donc nul (voir Figure P2).
En pratique [FRE 13][OUZ 135], le clapet de choc ne se ferme pas instantanément, induisant une variation initiale de pression (&p)1 au point C qui est inférieure à la variation théorique. La condition pratique d'ouverture du clapet de refoulement s'écrit alors :
|
(T33.1') v0 > (1/W) (g/a) h U |
avec W coefficient d'instantanéité de fermeture du clapet de choc (W < 1). Ce coefficient dépend fortement de la technologie utilisée pour résister à la fermeture du clapet de choc durant sa course. Pour une technologie à résistance constante (clapet rappelé par son poids propre, poids additionnel ou contre-poids extérieur), W vaut généralement 0,9. Pour une technologie à résistance croissante (clapet rappelé par ressort), W vaut généralement 0,5 voire moins. W peut se calculer si la pression limite (PL) est connue (T37.1).
La condition (T33.1'), appelée "contrainte de l'onde de choc suffisante", est primordiale et limite la hauteur de refoulement (H maxi) comme suit, que cette hauteur soit artificielle (H* correspondant à une conduite de refoulement bouchée par exemple) ou réelle (H limite) :
|
(T33.1'') H maxi = h + W (a/g) v0 |
En se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), la condition (T33.1') se simplifie en :
(T33.1''') j opt < (1/2)(1/g)(1/h) (W a/U)2
Pour un rapport h/H petit devant 1, cela s'écrit :
(T33.3) (H2)/h < (1/2)(1/g)(W a)2 (1 / j opt)
Si, de plus, la perte de charge linéaire dans la conduite motrice est prépondérante (ce qui s'écrit : j # u L/D), ce qui est le cas d'une conduite motrice étroite et/ou longue, alors cela s'écrit finalement :
(T33.3') (L/D)(H2)/h < (1/2)(1/g)(1/u)(W a)2
En pratique, cette condition est toujours vérifiée, sauf dans les cas courants suivants :
1- la vanne de réglage qui limite le débit de l'eau dans la conduite motrice se trouve trop fermée et induit dans cette dernière une importante perte de charge singulière supplémentaire (fh).
2- la vitesse a de l'onde de choc est insuffisante. Une conduite motrice en PVC rigide peut alors ne pas convenir (voir Remarque du T12.0' et [COD]).
3- le rapport ( H / (h)1/2 ) est excessif (voir Comparaison avec les abaques des fabricants)).
4- le rapport ( L/h ) est excessif (voir Comparaison avec les abaques des fabricants)) et induit dans la conduite motrice une importante perte de charge linéaire.
(T33.4) Remarque : lorsque la hauteur h est trop petite par rapport à la hauteur H, une solution consiste à utiliser deux béliers superposés (appelé également "double bélier" ou "bélier sur bélier") [BOL-LEB 145][ANO 235], un premier bélier à fort débit refoulant l'eau de source dans une colonne de chute verticale, un second bélier étant alimenté par cette chute et refoulant l'eau à la hauteur H imposée.
Application numérique : si h = 3 m et W = 0,9 ; on doit avoir :
cas 1 : j opt < 290 si H = 30 m et a = 1300 m/s
cas 2 : a > 297 m/s si j opt = 15 et H = 30 m
cas 3 : H < 120 m si j opt = 15 et a = 1300 m/s
cas 4 : L/h < 19 si H = 30 m ; a = 1300 m/s ; u = 0,02 ; D petit = 0,005 m ; f = 3 ; fh = 6
En fin de phase 3, le clapet de refoulement doit impérativement se fermer, sous peine d'interrompre le cycle de fonctionnement du bélier.
Cette condition est toujours vérifiée vu que la vitesse de l'eau dans la conduite motrice diminue à chaque passage de l'onde de pression (voir Phase 3).
(T34.1) La fermeture doit être cependant la plus rapide possible afin d'éviter que l'eau refoulée ne revienne en arrière. Les meilleurs résultats semblent obtenus avec des clapets à disque plat sur siège annulaire, légères, petites et multiples, avec ressort réglable [BER 104][REN 41]. Les clapets constitués par un simple cuir lesté donnent des résultats irréguliers et les petits béliers du commerce, montés presque toujours avec un clapet de ce type, ont une caractéristique U (U # H/h - 1) qui ne dépasse généralement pas la valeur de 15 [REN 41].
En fin de phase 4, le clapet de choc doit impérativement s'ouvrir, sous peine d'interrompre le cycle de fonctionnement du bélier. Juste après la fermeture du clapet de refoulement, la dernière onde descendante N dans la conduite motrice (dépression (&p)N) se réfléchit sur le clapet de choc également fermé, ce qui a pour conséquence [FRE 7] de changer le signe de la variation de vitesse de l'eau (&v)N sans changer le signe de la variation de pression (&p)N. Le clapet de choc s'ouvre alors sous la double dépression (d'intensité égale à 2 (&p)N). Pour cela, cette double dépression doit être suffisante et vérifier la condition suivante :
(T35.1) 2 (&p)N + (F3 / Sc) > r g h
où F3 est la résistance du clapet de choc à sa fermeture en fin de phase 3.
Par ailleurs, aux pertes de charges près dans le clapet de refoulement, cette dépression vaut approximativement :
(T35.2) (&p)N # r g (H - h)
Une condition de fonctionnement suffisante est donc la suivante :
(T35.2a) h/H < 2/3
Remarque : Cette relation est un peu différente de celle donnée par tous les auteurs (voir Comparaison avec les abaques des fabricants) dans la mesure où ils supposent a priori que l'ouverture du clapet de choc se produit par la dépression incidente et non par la dépression réfléchie, auquel cas la condition de fonctionnement est la suivante :
|
(T35.3) h/H < 1/2 |
En fonctionnement normal du bélier, cette condition peut être ajustée facilement par le choix approprié de la hauteur h.
En revanche, au lancement du bélier, la hauteur d'eau dans la conduite de refoulement est égale, au plus, à la valeur h.
(T35.4) Un amorçage du bélier est donc indispensable :
- Solution 1 : soit en remplissant par le haut la conduite de refoulement jusqu'à respecter la condition (T35.3), puis en repoussant à la main le clapet de choc pour démarrer le cycle (une seule fois suffit). Cette solution présente le risque d'introduire de l'air dans la conduite de refoulement.
- Solution 2 : soit en repoussant plusieurs fois le clapet de choc jusqu'à ce que l'eau soit suffisamment montée dans la conduite de refoulement pour que le cycle démarre ensuite automatiquement [OHA 6][SCH][CHA 40]. Pour aller encore plus vite, il suffit de fermer la vanne d'arrêt de la conduite de refoulement, faire monter en pression la cloche à air en actionnant le clapet de choc manuellement plusieurs fois, réouvrir la vanne d'arrêt, et répéter ce cycle de manoeuvre deux ou trois fois pour remplir suffisamment en eau la conduite de refoulement.
Si la conduite motrice vient d'être vidangée, il faut en préalable purger la conduite pendant environ 10 secondes (en maintenant ouvert le clapet de choc) jusqu'à ce que le jet d'eau sortant du clapet de choc soit dense et continu, sans "glouglous" particuliers.
(T36.0) Sous la pression statique due à la colonne d'eau dans la conduite de refoulement (p statique = patm + r g H), l'air de la cloche se dissous lentement dans l'eau jusqu'à saturation (environ 0,02 litres d'air dissous par litre d'eau à 20°C). Les eaux de source très pures et froides absorbent des quantités d'air importantes, au contraire des eaux de rivière [REN 56, 66].
Il est nécessaire de renouveler automatiquement cet air dissous qui s'échappe à chaque cycle avec l'eau refoulée par la conduite de refoulement (plusieurs litres d'air par mois selon les béliers).
Il existe deux conceptions pour l'aspiration de l'air depuis l'extérieur :
Cas n°1 : Aspiration directe par l'obturateur du clapet de choc
- Technologie : Une rainure est souvent pratiquée entre le clapet de choc et le piège à air [SCH] mais cela n'est même pas parfois nécessaire (cf certains béliers construits par Didier Nébréda).
- Conditions de fonctionnement : A chaque cycle du bélier, l'air aspiré doit pouvoir migrer rapidement à contre-sens depuis la prise d'air (obturateur) vers le piège à air (colonne d'eau située sous le clapet de refoulement) de façon à ne pas être éjecté au cycle suivant par le flux d'eau qui redescend dans la conduite motrice.
Cela nécessite que la distance horizontale (do) entre l'obturateur et le piège à air soit relativement petite (inférieure à 10 cm environ), et sans aucune niche ni contre-pente pendant cette migration. Mieux : si la pente est positive, le bélier devient une véritable pompe à air ! Voir pour exemple un des béliers de Didier Nébréda : pique du nez 2 (YouTube, 01:04). A noter dans cette vidéo : l'éjecteur incliné à 45° en sortie de clapet de choc permet de faire monter rapidement l'air au niveau du té puis dans le haut de la conduite horizontale. L'air piégé est assuré ensuite d'être chassé vers le clapet de refoulement au cycle suivant.
- Réglage du débit d'air : Ce réglage est très délicat voire problématique (le bélier pouvant s'arrêter si trop d'air est aspiré). Sur les béliers de fabricants, c'est un réglage d'usine. Sur certains béliers expérimentaux, on peut faire varier la distance (do) ou l'inclinaison de l'éjecteur ou parfois aussi (pour les clapets verticaux) la hauteur (ho) de l'obturateur par rapport au corps du bélier.
- Fonctionnement en mode noyé pour le clapet de choc : impossible.
Cas n°2 : Aspiration par un système autre que l'obturateur
- Technologie : Pour les petits béliers ou les faibles hauteurs de refoulement, un reniflard est placé généralement juste en dessous du clapet de refoulement [ANO 230]. Il est parfois placé en amont du corps (béliers Walton) avec risque de voir l'air remonter dans la conduite motrice si sa pente est importante [REN 57, 66][ANO 237]. Pour les autres cas, une pompe à air automatique doit être prévue [REN 57][ANO 222, 230].
- Conditions de fonctionnement : Le clapet de choc doit se fermer rapidement (afin d'induire un coup de bélier de bonne qualité suivi d'une dépression de même qualité). La distance horizontale (dr) entre la sortie du reniflard et le piège à air doit être relativement petite (inférieure à 3 cm environ), et sans aucune niche ni contre-pente pendant la migration de l'air aspiré, afin que ce dernier ne soit pas chassé au cycle suivant par le flux d'eau qui redescend dans la conduite motrice. La distance (do) ou la hauteur (ho) ne doit pas être trop petite afin de ne pas retomber dans le Cas n°1. La distance (do) ne doit pas être trop grande non plus sous peine de rendre inopérationnel le reniflard (fait constaté mais cause inconnue).
- Réglage du débit d'air : Un pointeau est généralement utilisé [BER 102][REN 58], lequel permet également de contrôler visuellement le non-bouchage de l'orifice. On peut utiliser aussi une vanne 1/4 tour à sphère qui a l'avantage de se boucher difficilement avec les impuretés (le passage de l'air étant en section pleine et non annulaire). Pour certains béliers, le réglage n'est pas linéaire et l'aspiration fonctionne quasiment en tout ou rien selon l'ouverture du pointeau (fait constaté et cause inconnue).
- Fonctionnement en mode noyé pour le clapet de choc : possible sans problème. Pour certains béliers cependant, il ne faut pas noyer complètement le clapet de choc (fait constaté et cause inconnue).
Démonstration du 0,02 litre d'air dissous par litre d'eau à 20°C
L'air sec contenant essentiellement 21 % d'oxygène (O2) et 79 % d'azote (N2) en fraction molaire, leur pression partielle (P_i) dans l'air sous pression P dans la cloche s'écrit :
P_O2 = 0,21 P
P_N2 = 0,79 P
Ces deux gaz étant peu solubles dans l'eau, leur fraction molaire ou solubilité (x_i) dans l'eau est donnée par la loi de Henry sous la forme :
x_O2 = k_O2 P_O2
x_N2 = k_N2 P_N2
où k_i est la constante de Henry qui vaut (cf [UQAC]) : (k_O2 = 2,58 10-5 / patm) et (k_N2 = 1,32 10-5 / patm) à la température de 20°C (ou température T = 273 + 20 en °K).
avec patm = 101325 Pa
La quantité en nombre de moles (n_i) de chacun de ces gaz par rapport à une quantité d'eau donnée (n_eau) s'obtient à partir de leur fraction molaire (x_i) sous la forme :
x_O2 = n_O2 / (n_O2 + n_eau) # n_O2 / n_eau
x_N2 = n_N2 / (n_N2 + n_eau) # n_N2 / n_eau
et l'on peut écrire l'expression du nombre de moles d'air dissous dans n_eau moles d'eau sous la forme :
n_air_dissous = n_O2 + n_H2 # n_eau y P
avec : y(T) = 0,21 k_O2 + 0,79 k_N2
Compte tenu de la masse volumique (r = 1000 kg/m3) et de la masse molaire de l'eau (M = 0,018 kg/mol), la quantité n_eau s'écrit pour un volume d'eau donné (v_eau) :
n_eau = r v_eau / M
Le volume d'air dissous (v_air) suit par ailleurs la loi des gaz parfaits sous la forme :
P v_air = n_air_dissous R T
avec R = constante des gaz parfaits (R = 8,314 J/(K mol))
et T = température en °K
D'où l'expression de la concentration d'air dissous dans l'eau :
|
v_air / v_eau = r y(T) R T / M |
qui donne numériquement 0,021 litre d'air dissous par litre d'eau à 20°C
Dans une eau plus froide (température de 0°C), la constante de Henry vaut (cf [UQAC]) : (k_O2 = 3,98 10-5 / patm) et (k_N2 = 1,86 10-5 / patm)
qui donne numériquement 0,029 litre d'air dissous par litre d'eau à 0°C
On constate que ce volume d'air dissous dans l'eau est indépendant de la pression (P) dans la cloche.
En revanche, la loi des gaz parfaits indique que la masse d'air dissoute est proportionnelle à la pression P.
Toute l'installation (en particulier la cloche à air) doit résister aux sollicitations mécaniques qui sont de quatre types :
Pression limite (PL)
Cette pression est la pression effective (pF - patm) du fluide en situation limite donnée par (T33.1") :
(T37.1) PL = (pF - patm) maxi = r g H maxi = r g h + r a v0 W
Cette pression limite est la somme de la pression statique effective dans la conduite motrice (r g h) et de la pression dynamique (r a v0) créée par l'onde de choc en fin de phase 2, cette dernière étant corrigée d'un facteur W d'instantanéité de fermeture du clapet de choc (r a v0 W).
Tous les composants (conduite, coude, té, raccord, réduction, vanne, manomètre, cloche, clapet...) doivent résister à cette pression limite.
Tous les composants doivent aussi être parfaitement étanches à l'eau et à l'air, à la fois :
- au niveau des assemblages entre pièces non filetées (avec joint toujours en compression, plat graphité ou torique NBR),
- au niveau des raccordements entre pièces filetées (avec filasse toujours en contact avec l'eau et non avec l'air)
- au niveau des jonctions définitives avec pièces rapportées (avec soudure de qualité si piquage).
Application numérique : si h = 3 m ; a = 1300 m/s ; v0 = 1 m/s ; W = 0,9 on trouve :
PL = 12,0 105 Pa = 12 bar
Chocs et vibrations
Les chocs et vibrations induites altèrent toutes les fixations. Il convient notamment de freiner toutes les vis (par exemple par rondelle Grower et/ou écrou Nylstop), y compris celles des cadrans de manomètre (préférer les cadrans sertis). Il convient également de choisir des colliers de serrage qui soient indéformables (par exemple pour la cloche, entre son corps et son bol).
Les chocs et vibrations altèrent également les organes en mouvement. Pour les manomètres ayant un cadran à aiguille, il convient de les isoler en interposant un robinet de contrôle (pour prise de mesure).
Fatigue des organes en mouvement
Certains organes en mouvement fatiguent vite s'ils ne sont pas bien choisis et/ou dimensionnés. C'est le cas des ressorts dont les spires sont mal calculées en résistance à la fatigue (le calcul simplifié consistant à diviser par trois la résistance élastique au glissement Reg). Par ailleurs, pour les ressorts à traction, ils cassent souvent à la jonction entre la dernière spire et le crochet (préférer des ressorts à crochets indépendants, tournants ou vissés). Pour les balanciers à contre-poids sur les clapets de choc, ils peuvent casser à leur encastrement sur l'obturateur du clapet (tige du balancier à bien dimensionner).
Usure des organes en mouvement
Deux organes en mouvement l'un par rapport à l'autre s'usent rapidement si leur conception et/ou leur matériau sont mal choisis. C'est le cas du guidage de l'obturateur des clapets (pour le clapet de refoulement, préférer un clapet à disque non guidé axialement ; pour le clapet de choc, préférer un clapet à disque et culbuteur). C'est le cas aussi de l'axe de rotation du culbuteur éventuel (éviter les roulements à billes qui supportent mal la forte humidité et la poussière ambiante, et préférer un palier lisse avec si possible une boîte à graisse).
Lorsque l'usure est inévitable, prévoir un système de compensation automatique du jeu. Pour les clapets de choc à disque et culbuteur, le ressort de traction compense quasi-parfaitement le jeu existant au niveau de l'axe de rotation du culbuteur, en ramenant systématiquement le disque du clapet dans l'axe du flux d'eau.
Les fabricants de béliers proposent généralement des abaques pour calculer le point de fonctionnement du bélier (diagramme des "puissances"), les limites du rapport h/H (diagramme des chutes), la longueur pratique L, le rapport optimal (v0 / vm) entre vitesses, le volume d'air de la cloche (volairatm) et la pression effective (pF - patm) maximale de la cloche.
Le point de fonctionnement du bélier correspond à l'Alimentation continue en eau.
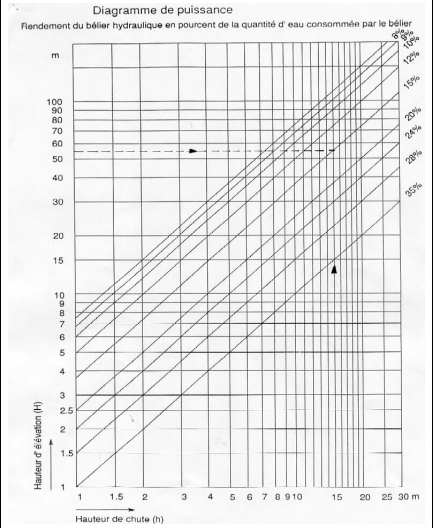
[SCH][COD] présentent une série de courbes donnant log(H - h) en fonction de log(h) pour différentes valeurs du rapport (qF / qB), la notation "H" de leur diagramme correspondant à notre notation "H - h". Voir Figure ci-dessus ou diagramme de puissance.
Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), et compte tenu de (P2)(T22.5)(T24.1), le calcul de ce rapport donne :
(T4.1) (qF / qB) opt # (3/4)(1/U) / ( 1 + (3/4)(1/U) + (3/2)(t1 / T opt) )
Compte tenu de (T13.4')(T21.2), cela s'écrit :
(T4.1') log(H - h) # log(h) + log(A)
avec :
A = ( 1/((qF / qB) opt) - 1 ) / ( (4/3) + 2 (t1 / T opt) ) # (3/4)( 1/((qF / qB) opt) - 1 )
En échelle logarithmique, la courbe log(H - h) en fonction de log(h) est donc quasiment une droite, tout comme le diagramme du fabricant (la notation "H" de ce diagramme correspondant à notre notation "H - h").
Par ailleurs, pour une valeur moyenne de (t1 / T opt) égale à 1/4, le calcul donne alors, par exemple en h = 30 m, des valeurs de (H - h) égales à 30 m ; 52 m ; 120 m (pour des rapports respectifs de 0,35 ; 0,24 ; 0,12) alors que l'abaque du fabricant donne 30 m ; 60 m ; 150 m.
Le calcul général et l'abaque sont donc très proches.
[REN 60 figure 27, 79 tableau B][CAR 78 tableau IV.1.7.2][ANO 233 Tableau] présentent une série de courbes donnant le rapport (h/L) fonction de (qB) pour différentes valeurs de D.
Pour un joint relativement rigide du clapet de choc (K grand donc Z = 0), en se plaçant autour du point de fonctionnement optimal (v0 opt) du bélier (T26.0), et compte tenu de (P2)(T22.5)(T24.1), le calcul de qB donne :
(T4.2) qB opt # (1/2) S (v0 opt) B
avec :
B = ( 1 + (3/4)(1/U) + (3/2)(t1 / T opt) ) / ( 1 + (3/4)(1/U) + (3/4)(t1 / T opt) )
Compte tenu de (T16.3)(T26.0), cela s'écrit :
(T4.2') qB opt # (π / 16) B (D2) (2 g h / j)1/2
avec j donné par (T16.2).
Si on suppose que les quantités (t1 / T opt) et (1/U) sont petites devant 1 et que la perte de charge linéaire dans la conduite motrice est prépondérante (ce qui s'écrit : j # u L/D), alors cela se simplifie en :
(T4.3) h/L # (128 / (π2)) (1/g) u (1/(D5)) (qB opt)2
La courbe (h/L) en fonction de (qB opt) est donc une parabole f(x) de type : f(x) = a (x2), tout comme l'abaque du fabricant.
Par ailleurs, le calcul donne, par exemple en D = 66 mm, des valeurs de L/h égales à 8 ; 9 ; 11 ; 13 (pour des débits qB de 150 l/mn ; 140 l/mn ; 125 l/mn ; 114 l/mn) alors que l'abaque du fabricant donne 7 ; 8 ; 10 ; 12.
Le calcul simplifié et l'abaque sont donc très proches.
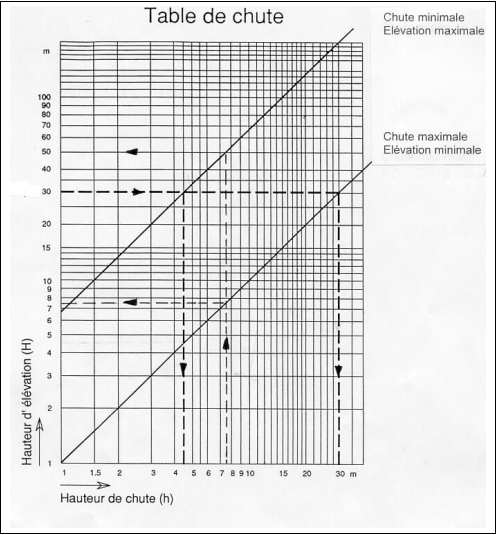
[SCH][COD] présentent un diagramme donnant les limites du rapport h/H sous la forme : log(h) < log(H - h) < log(h) + log(7), la notation "H" de leur diagramme correspondant à notre notation "H - h". Voir Figure ci-dessus ou table de chute. Ce qui est équivalent à : 2 h < H < 8 h.
[REN 46, 38, 42] indique la fourchette : 2 h < H < 15 h
[CAR 74, 75, 78] indique la fourchette : 2 h < H < (20 h à 25 h, et 30 h pour de faibles valeurs de h)
[BOL-LEB 141] indique un maximum pour H tel que : H - h < 25 h, soit : H < 26 h
[ANO 227] indique un minimum pour H tel que : H > 3 h
Notre calcul de la limite basse pour h/H correspond à l'Ouverture du clapet de refoulement.
En particulier, si l'on considère une ancienne conduite motrice en fonte de rapport (D/e) valant environ 50, compte tenu de (T12.0'), la vitesse d'onde vaut alors environ 750 m/s.
Compte tenu de (T33.3) et des hypothèses associées, pour un clapet de choc rappelé par son poids propre et poids additionnels (W = 0,9), pour un coefficient j valant en moyenne 20, la hauteur H maximale vaut alors environ : 34 (h)1/2.
Ce qui donne une limite basse pour h/H égale à : 1/34 ; 1/24 ; 1/20 ; 1/17 quand h vaut respectivement : 1 m ; 2 m ; 3 m ; 4 m. Pour une hauteur motrice h pas trop petite (entre 2 et 4 m), on retrouve grosso-modo le résultat de l'ensemble des auteurs.
Notre calcul de la limite basse pour h/H est donc plus général que celui des auteurs, [CAR] étant celui qui s'approche le plus de notre calcul.
Remarque 1 : [BER 102, 105] signale le cas performant d'un bélier Lacroix fonctionnant avec une hauteur h = 0,40 m et un rapport ( h / (H - h) ) valant 1/75, soit h/H = 1/76, ainsi que le cas d'un bélier Decoeur fonctionnant avec une hauteur h = 0,30 m et un rapport ( h / (H - h) ) valant 1/30, soit h/H = 1/31.
Remarque 2 : [BOL-LEB] signale le cas performant d'un bélier Bollée élevant l'eau à une hauteur H de 126 m et sur une distance L' de 8 km.
Concernant notre calcul de la limite haute pour h/H, il donne le même résultat (égal à 1/2) que la plupart de ces auteurs et correspond à l'Ouverture du clapet de choc.
[REN 45, 60][CAR 76] indiquent la fourchette : 6 h < L < 12 h, et l'attribuent aux limites respectives de fonctionnement (vol3 = 0) et (Rg = 0). [REN 60 Fig.27] reporte cette fourchette sur le diagramme des "puissances".
[ANO 226] indique la même fourchette : 6 h < L < 12 h, mais l'attribue aux limites respectives de fonctionnement (vol3 = 0) et (onde de choc suffisante).
[SCH][COD] indiquent la fourchette : 3 h < L < 5 h.
Notre calcul de la longueur L optimale donne un résultat proche de [REN][CAR] (voir (T26.6) et (T33.3')).
Chacun des auteurs [BER 91][REN 30][CAR 73] traite la recherche de l'optimum d'un bélier à travers son rendement, selon une approche personnelle parfois difficile à suivre, et sans consensus entre auteurs.
Notre calcul du rapport optimal (x opt) est au contraire basé sur l'optimum du débit moyen refoulé (qF) et donne un résultat simple (voir Conclusion partielle - relation (T26.5)). Ce résultat est en outre identique à celui de [REN 34].
[BER 101][REN 56][CAR 78][MOR 221] indiquent une formule empirique qui fait consensus, à savoir que le volume d'eau refoulé à chaque cycle doit être une faible fraction du volume d'air de la cloche, soit de 2 à 5 % environ.
Compte tenu de (T18.61)(T26.11.21)(T26.11.22), on peut écrire :
(T4.4) vol3* / volairatm = (1 / Q8) (Rr - 1) / Rr
avec :
Q8 = (Rr + P8)2 / ( 2 Rr P8)
P8 = patm / (r g H)
Cette quantité Q8 reste toujours comprise entre 2 et 5 quand (P8 / Rr) varie de 1/8 à 8, ce qui correspond, pour un ratio Rr égal à 1,1, à une hauteur H comprise entre 75 m et 1 m.
On trouve alors que le rapport vol3* / volairatm est compris entre 1,8 % et 4,6 %, ce qui est en très bon accord avec la plage de 2 à 5 % donnée par les auteurs pré-cités.
Notre calcul donne toutefois un résultat exact en toutes circonstances, pour un volume volairatm non minimal et une hauteur H quelconque (voir Conclusion partielle - Dispositif de refoulement).
[PIL] indique que les cloches Pilter sont éprouvées à 10 bars.
Notre calcul (T37.1) de résistance de la cloche donne une valeur un peu supérieure, mais tient compte d'un éventuel mauvais dimensionnement du dispositif de refoulement, lequel induit une montée de pression non prévue dans la cloche.
 Dernière mise à jour de la page : 21 septembre 2025.
Dernière mise à jour de la page : 21 septembre 2025.