| In English | Accueil/Contact | Billard | Bélier | SNH | Relativité | Botanique | Musique | Ornitho | Météo | Aide |
| Théorie du jeu | Pratique du billard | Bibliographie |
L'auteur R. Petit a publié l'article "La pratique du Billard" dans le Magazine Pour La Science N°246 en avril 1998.
Cet article, publié également sur le site Web "Pour la Science", n'est plus disponible actuellement. Le texte intégral de l'article Web est reproduit ci-dessous. En complément ont été rajoutés :
- Les figures 1 à 4 produites par J.A. Gomez Valderrama et issues de son simulateur VRCarom ;
- Les figures 5 et 6, provenant du livre de R. Petit : Billard - Théorie du jeu (voir Bibliographie) ;
- Le Glossaire et les Résultats issus de la mécanique, provenant du livre de R. Petit : Billard - Théorie du jeu (voir Bibliographie) ;
- La Démonstation de ces résultats, produite par R. Petit sur ce site.

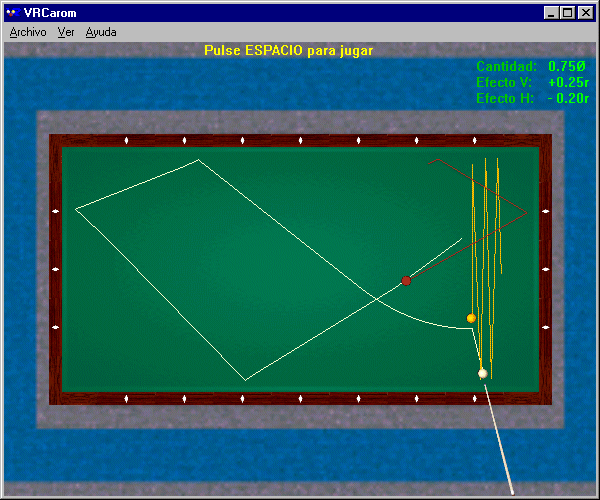
Figure 1 ci-dessus : "coulé" par trois bandes avec contournement de la bille numéro 3
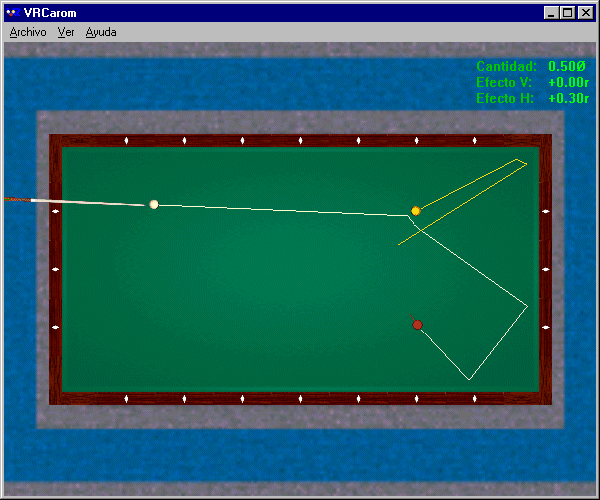
Figure 2 ci-dessus : Coup par deux bandes
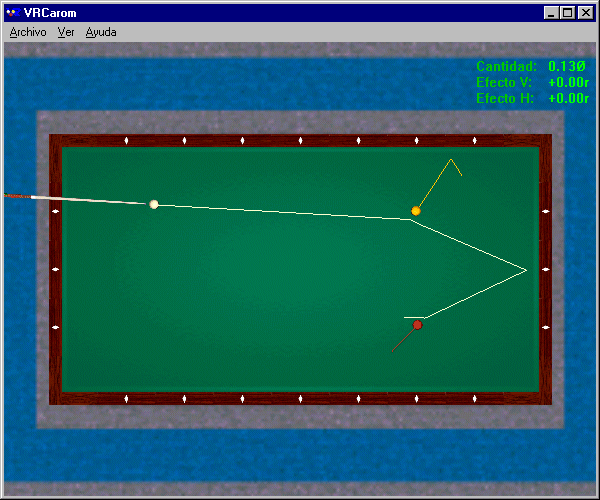
Figure 3 ci-dessus : Coup par une bande
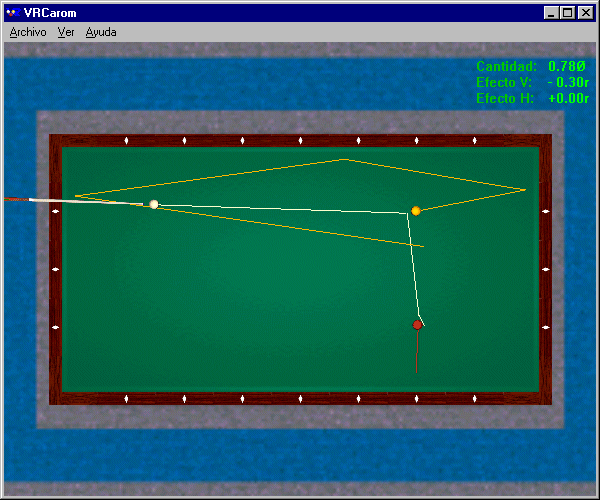
Figure 4 ci-dessus : Coup direct
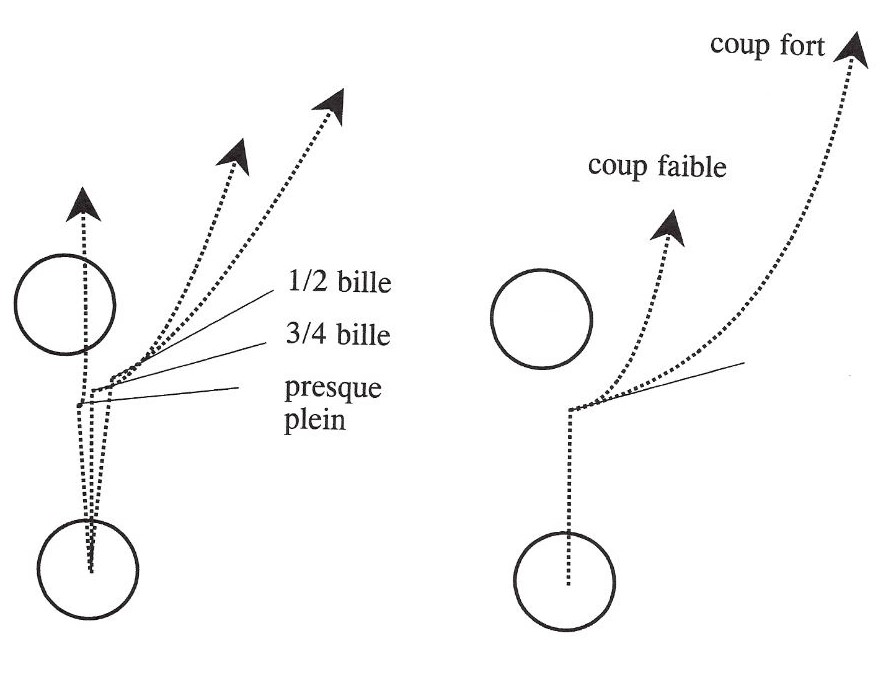
Figures 5 ci-dessus : Réglage de la quantité de bille (figure de gauche) ; Réglage de la force du coup de queue (figure de droite)
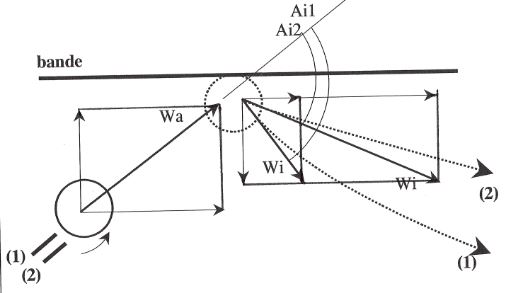
Figure 6 ci-dessus : Réglage de l'effet de côté
Régis Petit. La connaissance des lois de la physique assure une pratique raisonnée et plus sûre. Elle détermine et explique les réglages utilisés par le joueur.
Il existe plusieurs types de billards. Le billard du mathématicien est un billard puissamment idéalisé où les billes sont des points, où les frottements n'existent pas, et où les lois de rebond sont celles de l'optique. Ce billard, dit le physicien, n'a pas de réalité. Le physicien imagine un billard moins idéalisé, où les frottements influent sur la trajectoire des billes, mais il n'a pas l'intelligence "du bout des doigts" du praticien. Nous allons examiner ici comment les règles physiques et mathématiques nous aident à pratiquer ce noble jeu.
Le jeu de billard actuel existe depuis environ un siècle et rassemble de plus en plus d'adeptes, en particulier le billard français ou "carambole" qui se joue avec trois billes et selon cinq spécialités : partie libre, jeux de cadre, jeu par une bande, jeu par trois bandes, billard artistique. L'une d'elles, le "trois bandes", s'est développée à l'étranger, principalement aux états-Unis et au Japon ; les échanges sur Internet, notamment dans le groupe "rec.sport.billiard", sont riches d'enseignements.
Le billard est avant tout un jeu de pratique, fondé sur la connaissance et la maîtrise d'un certain nombre de techniques (par exemple, le "rétro", le "coulé", le "massé", etc.) et de tactiques (par exemple, le "placement", le "rappel", l'"amorti", etc.). La théorie du billard est fondée uniquement sur la mécanique du solide. Le premier traité théorique sur la mécanique des effets du jeu de billard est à notre connaissance celui de G.G. Coriolis, publié en 1835. D'autres traités ont ensuite suivi, tant en France qu'à l'étranger. Entre ces deux approches, l'une très pratique et l'autre très théorique, rares sont les ouvrages qui font le lien ou la synthèse. Est-il vraiment possible d'aborder la pratique du billard sous l'angle de la mécanique et des mathématiques ? Existe-t-il une "pratique raisonnée" du billard ? Dans mon livre récemment paru (voir la bibliographie), et dont cet article est inspiré, les lecteurs intéressés trouveront les justifications mathématiques des affirmations présentées ici.
Pour répondre à la question : "Comment utiliser les connaissances de mécanique ?", nous prendrons pour exemple la réalisation d'un "coulé" par trois bandes avec contournement de la bille numéro 3 (voir Figure 1). L'objectif est de choquer la bille numéro 2 avec la bille numéro 1, puis de contourner la bille numéro 3, de faire le tour du billard en choquant successivement les trois bandes, et enfin de faire le point sur la bille numéro 3. Pour ce coup, quatre réglages suffisent, la hauteur d'attaque, la quantité de bille, la force du coup de queue et l'effet de côté.
Le premier réglage que doit maîtriser tout joueur de billard est ici la hauteur d'attaque prise sur la bille numéro 1. Trois possibilités sont offertes a priori au joueur : attaque plus ou moins basse ; plus ou moins haute ; très haute. L'objectif à atteindre est de choquer la bille numéro 2, puis la grande bande située derrière cette bille. La mécanique du mouvement des billes nous enseigne que, après un choc entre deux billes, la trajectoire de chaque bille est une courbe parabolique, suivie éventuellement d'un segment de droite. Pour obtenir une courbe dont la concavité est tournée vers l'avant et qui frappe la grande bande avant la petite, il faut animer la bille numéro 1 d'une forte rotation en avant pour que cette bille puisse se rabattre le plus rapidement possible vers la grande bande, après le choc entre billes. En pratique, cela s'obtient par une attaque très haute de la bille numéro 1.
Le second réglage à maîtriser est ici la quantité de bille prise sur la bille numéro 2. à nouveau, trois possibilités sont offertes au joueur : 1/2 bille ; 3/4 bille ; presque plein. L'objectif est de contourner la bille numéro 3 après le choc sur la bille numéro 2. La mécanique des chocs entre deux solides nous apprend que, juste après un choc parfaitement élastique entre une bille mobile et une bille immobile de même masse, la bille mobile rebondit toujours en suivant la tangente au point de choc. Pour éviter au maximum la bille numéro 3, il faut donc relever cette tangente le plus possible, tout en gardant suffisamment de vitesse pour choquer ensuite les trois bandes. En pratique, le 1/2 bille ne relève pas suffisamment la tangente. Le presque plein permet bien d'éviter la bille numéro 3, mais amortit trop la bille numéro 1 sur la bille numéro 2. Un bon compromis consiste à prendre une quantité de bille égale à environ 3/4 bille (voir Figure 5 de gauche).
Le troisième réglage à maîtriser est ici la force du coup de queue, qui détermine la vitesse de la queue au moment du choc sur la bille numéro 1. Trois possibilités sont encore offertes au joueur : coup de queue faible ; moyen ; fort. L'objectif est de minimiser les risques de collision lors du contournement de la bille numéro 3. Nous avons vu précédemment que la bille numéro 1 rebondit sur la bille numéro 2 en suivant la tangente au point de choc. Pour éviter la bille numéro 3, la bille numéro 1 doit suivre cette tangente le plus longtemps possible. Cela s'obtient par un coup de queue puissant (voir Figure 5 de droite).
Le quatrième réglage est ici l'effet de côté mis sur la bille numéro 1. Trois possibilités sont encore offertes a priori au joueur : effet de côté naturel ; nul ; contraire. L'objectif est de régler correctement le rebond de la bille numéro 1 sur la première bande choquée, afin de faire le point en trois bandes sur la bille numéro 3. La mécanique nous enseigne que, juste après un choc contre une bande, la bille numéro 1 rebondit différemment selon l'effet de côté mis sur la bille (voir Figure 6) :
Juste avant ce choc, la vitesse de translation de la bille (Wa) se décompose en une vitesse tangentielle et une vitesse perpendiculaire à la bande. Que se passe-t-il alors juste après le choc ?
Sans effet de côté (cas (1)), la vitesse perpendiculaire qui est rendue par la bande est diminuée par l'élasticité imparfaite de la bande ; la vitesse tangentielle est fortement diminuée par le frottement de la bille sur la bande. Ces deux paramètres déterminent l'angle (Ai1) de la vitesse de translation (Wi) de la bille avec la bande.
Avec un effet de côté naturel (cas (2)), la bille frotte beaucoup moins au moment du choc contre la bande. La seule modification par rapport au cas précédent concerne la vitesse tangentielle rendue par la bande, qui devient supérieure. La vitesse de translation (Wi) de la bille fait alors un angle (Ai2) plus petit avec la bande.
En pratique, pour faire le point en trois bandes sur la bille numéro 3, l'expérience montre qu'il faut mettre un peu d'effet de côté naturel sur la bille numéro 1.
Assemblons maintenant les différents réglages à réaliser : attaque très haute (pour ramener la bille numéro 1 vers la grande bande derrière la bille numéro 2); quantité de bille égale à 3/4 bille (pour contourner la bille numéro 3 sans trop amortir la bille numéro 1 sur la bille numéro 2) ; coup de queue puissant (pour minimiser les risques de collision pendant le contournement) ; effet de côté naturel (pour faire le point en trois bandes sur la bille numéro 3). N'est-ce pas là une "pratique raisonnée" correspondant à notre coup complexe ?
Que se passe-t-il pour un autre coup ? Y a-t-il d'autres réglages à maîtriser ? Oui. Trois autres réglages importent. Le cinquième réglage est l'inclinaison de la queue par rapport au tapis, qui permet d'exécuter des "massés", des "piqués" et des sauts de bille ; le sixième réglage est la masse de la queue, qui permet d'"alléger" plus ou moins le coup de queue et d'attaquer la bille plus près de son bord. Le septième et dernier réglage est le plus important de tous. Il concerne le choix de la meilleure tactique à adopter pour réussir le carambolage lorsque plusieurs solutions sont envisageables.
Prenons un exemple à la partie libre (voir Figure 2). L'objectif est de réussir le carambolage, c'est-à-dire de toucher avec la bille numéro 1 les deux autres billes, en passant ou non par les bandes. Trois possibilités sont offertes a priori au joueur : coup direct ; coup par une bande ; coup par deux bandes. La mécanique nous apprend que, lorsque la bille numéro 1 roule sans glisser sur le tapis juste avant le choc sur la bille numéro 2, il suffit de choquer la bille numéro 2 avec une quantité de bille égale à 1/2 bille pour toujours faire dévier la bille numéro 1 d'un angle final égal à 40 degrés environ ; cette déviation finale est de plus très peu sensible à une erreur de quantité de bille autour de ce 1/2 bille. Quelle aubaine ! Il suffit donc ici de choisir cette quantité de bille particulière et de jouer en deux bandes pour assurer sans risque le carambolage.
Les deux autres tactiques sont-elles aussi fiables ? Le coup par une bande (voir Figure 3) nécessite une quantité de bille proche du fin, et donc une extrême précision dans la visée, ce qui est très risqué en pratique. Le coup direct (voir Figure 4) demande une rotation arrière de la bille numéro 1 associée à une quantité de bille précise et, compte tenu de la distance élevée entre billes, un coup de queue de puissance donnée pour conserver cette rotation arrière au moment du choc entre billes ; ce qui est encore plus risqué. En pratique, c'est la tactique robuste en deux bandes qui est choisie par le joueur : attaque haute (pour mettre la bille numéro 1 en roulement sans glissement sur le tapis), quantité de bille proche du 1/2 bille (pour obtenir la déviation de 40°), coup de queue faible (pour ne pas disperser les trois billes), effet de côté à doser (pour régler le rebond sur la première bande et faire le point en deux bandes sur la bille numéro 3). N'est-ce pas là encore une "pratique raisonnée" correspondant à la situation présente du jeu ?
Pratique et théorie sont deux approches complémentaires, sans que la théorie puisse un jour remplacer la pratique. Seule la pratique, en effet, permet de progresser sur le plan de la régularité des performances. La théorie a plutôt une vertu pédagogique : elle permet de comprendre et de faire comprendre à autrui les réglages utilisés par le joueur. Pratique et théorie cohabitent ainsi en une "pratique raisonnée" du billard, et continueront de fasciner à la fois les joueurs et les théoriciens.
Adhérence pendant le choc : contact without slipping, or momentarily grabbing
Amorti : dead ball
Attaque basse/haute : below-center/above center hit
"Bande-avant" ou "Bricole" : rail-first shot or kick shot
Bande lisse/rugueuse : slippery/sticky cushion, or low/high friction cushion
Bande molle/dure : soft/hard cushion
Billard (table) : table
Billard français : carom billiards
"Bille collée" : frozen ball
Bille N°1, N°2 et N°3 : cue ball, first object ball and second object ball
"Bosse" ou "Contre" : double kiss (shot where the first object ball rebounds back into the cue ball)
"Butage" : cling or skid
Chevalet : bridge
Choc bille-tapis : ball-cloth collision
"Coulé" : follow shot
Coup de queue incliné, faible/moyen/fort : soft/medium/hard cue-elevated stroke
"Coup-dur" : kiss-back shot or double kiss, but only when the first object ball is close to or frozen to the cushion
Déviation initiale/finale : initial/final deflection angle
Effet de côté contraire, par rapport à la bande/bille N°2 : reverse or inside English
Effet de côté naturel ou "Bon effet", par rapport à la bande/bille N°2 : running or outside English
"Fausse-queue" : miscue
Force de frottement : friction force
"Glissement pur" : pure sliding
Hauteur d'attaque : height of the cue tip contact point
Limage : warm-up stroke
"Massé" : massé shot
Moment cinétique : angular momentum
Moment d'inertie : moment of inertia
Paramètre de pivotement : coefficient of boring friction or z-spin coefficient of friction
Patinage avant/arrière : forward/backward overspin or top-/back-overspin
Percussion : percussion
"Piqué" : piqué shot (massé shot aiming to move back the cue ball)
"Placement" : position play
Point d'appui de la bille : ball-cloth contact point
Point de choc : collision point
Point de visée : aiming point
Principe fondamental de la dynamique : Newton's laws of motion
Procédé : cue tip
"Quantité de bille" (plein, 3/4 plein, fin) : fullness of ball hit (full, 3/4-full, fine)
Quantité de mouvement : linear momentum
Queue légère/massive : light/heavy cue stick
"Queutage" : push shot (foul shot where the cue ball is close to or touching the object ball)
"Rappel" : gather shot
"Rencontre" : time shot (shot where the first object ball pushes the second object ball towards the cue ball)
"Renversé" : reverse-the-corner shot or double-the-rail shot
"Repère" : diamond
Résistance à l'avancement : rolling resistance
"Rétro" : draw shot
Roulement : rolling without slipping
Saut : jump shot
Spécialités (partie libre, jeu de cadre, jeu par 1 bande, par 3 bandes, billard artistique) : disciplines (straight rail, balkaline, one-cushion, three-cushion, artistic billiards)
Tapis : cloth
Vitesse de glissement : relative surface velocity
Vitesse de translation/rotation : translational/rotational velocity
Les équations générales qui modélisent le choc entre deux corps quelconques, compte tenu de l'élasticité et du frottement entre corps pendant le choc, sont données ci-après.
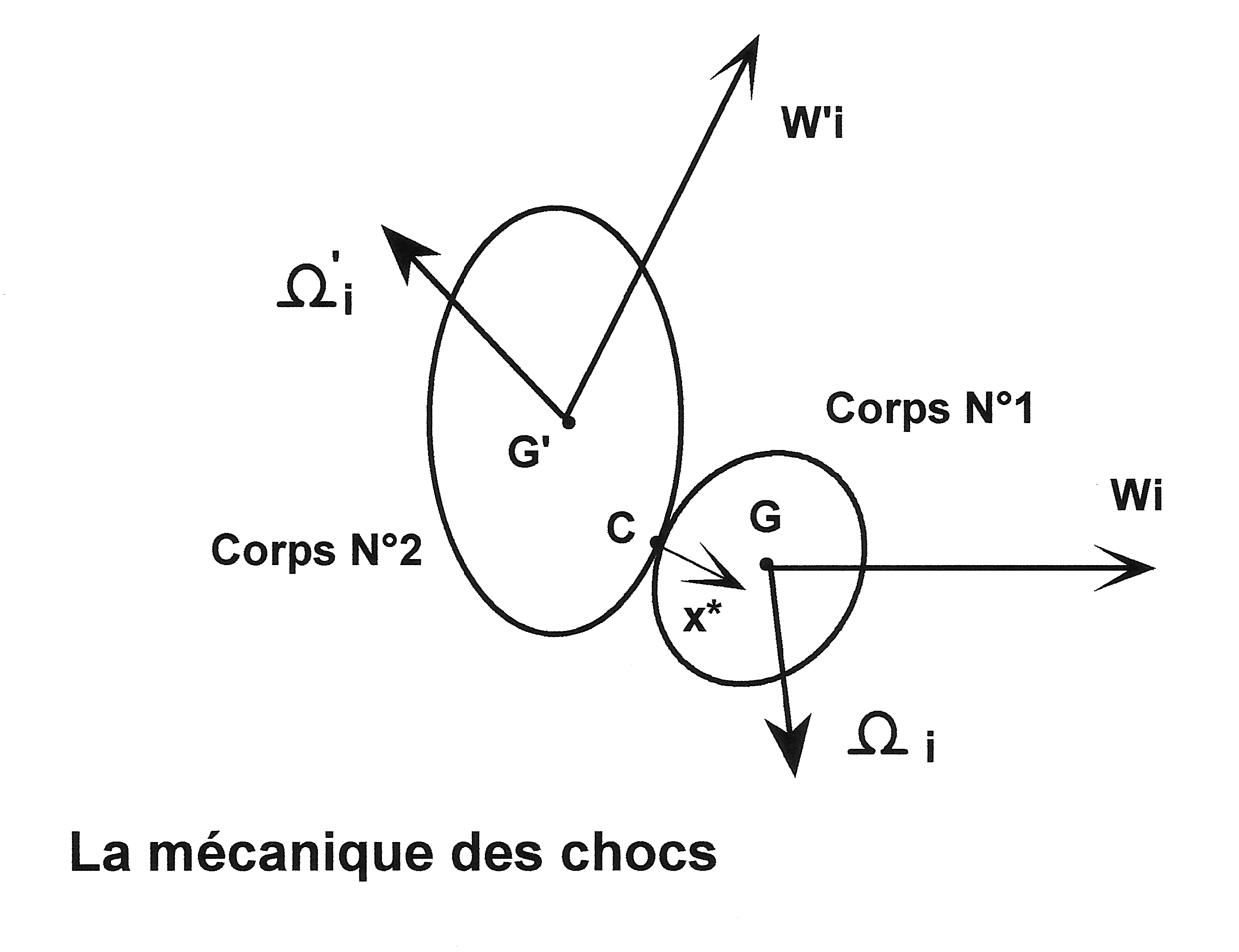
C, WC : point de choc entre corps, et vecteur vitesse de glissement de C dans le mouvement relatif du corps N°1 par rapport au corps N°2.
G, M : centre de gravité et masse du corps N°1
I, R : moment d'inertie par rapport au diamètre, et rayon du corps N°1 (pour un corps sphérique et homogène avec : I = (2/5) M R2)
P : vecteur percussion, s'exerçant en C et provenant du corps N°2
Q : énergie cinétique du système formé par les deux corps
x* : vecteur unitaire, normal à C et dirigé vers le corps N°1
W, Ω : vecteurs vitesse de translation et vitesse de rotation du corps N°1
' : indice relatif au corps N°2
a, i : indices relatifs aux instants juste avant et juste après le choc
fi, N : coefficients de frottement et d'élasticité entre les deux corps
e : pourcentage d'énergie cinétique qui est perdu pendant le choc
v1.v2 et v1 x v2 : produit scalaire et produit vectoriel des deux vecteurs (v1) et (v2).
v1 x v1 = 0
produit mixte : (v1 x v2).v3 = (v2 x v3).v1
double produit vectoriel : v1 x (v2 x v3) = (v1.v3) v2 - (v1.v2) v3
||v1||: norme du vecteur (v1) telle que : ||v1||2 = v1.v1
Les lois standards de la mécanique des chocs s'écrivent :
Conservation de la quantité de mouvement :
M Wi = M Wa + P
M' W'i = M' W'a + (-P)
avec vecteurs Wi et W'i à déterminer.
Conservation du moment cinétique :
I Ωi = I Ωa + GC x P
I' Ω'i = I' Ω'a + G'C x (-P)
avec vecteurs Ωi et Ω'i à déterminer.
Loi de Coulomb sur le frottement :
P = P* ( x* - fi WCa / ||WCa||)
P* = k M (W'a - Wa).x*
WCa = (Wa - W'a) - [ (Wa - W'a).x* ] x* + x* x (R Ωa + R' Ω'a)
avec constante (k) à déterminer.
Règle des collisions de Newton (pour des corps sphériques et homogènes) :
(Wi - W'i).x* = - N (Wa - W'a).x*
avec N constant.
Théorème de l'énergie cinétique :
Qa - Qi = e Qa
avec e non constant (si N est constant)
Q = (1/2) (M W 2 + I Ω2 + M' W'2 + I' Ω'2)
Il y a donc 5 équations pour 5 inconnues (Wi, Ωi, W'i, Ω'i, k). La résolution vectorielle donne pour solution unique (équations 1a) :
|
Wi = Wa + (P*/M) (x* - fi WCa / ||WCa||) Ωi = Ωa + (5/ 2R) fi (P*/M) x* x WCa / ||WCa|| W'i = W'a + (M/M') (Wa - Wi) Ω'i = Ω'a - (M/M') (R/R') (Ωa - Ωi) k = (1 + N)/(1 + M/M') |
On en déduit également que :
|
Wi.x* = k W'a.x* + (1 - k) Wa.x* W'i.x* = (k M / M') Wa.x* + (1 - k M / M') W'a.x* WCi = u WCa avec u = 1 - (7/2) fi (1 + M/M') (P* / M) / ||WCa|| e (1 + M / M') = (1 - N2) (1/2) M [ (W'a - Wa).x* ) ] 2 / Qa lorsque (fi) est négligeable. |
1- Dans le cas du choc bille-tapis dans lequel la bille rebondit sur le tapis après un saut en l'air, les équations trouvées sont exactes.
2- Dans le cas du choc entre deux billes, les équations projetées horizontalement sur le tapis sont exactes à condition de négliger l'influence des percussions horizontales provenant du tapis. En projection verticale, la petite vitesse de translation prise par chaque bille se trouve détruite par la résistance du tapis (lorsque la bille s'enfonce dans le tapis), ou est rendue insensible par le poids de la bille qui la ramène immédiatement contre le tapis (lorsque la bille saute en l'air). Les équations sont presque exactes à condition d'ignorer ou de forcer à zéro la vitesse verticale de translation de chaque bille (composante Wi.z et W'i.z).
S'il s'agit d'un choc parfaitement élastique entre deux billes de mêmes masses (condition : N = 1, M = M'), alors un choc supposé sans frottement (condition : fi = 0) ne fait qu'échanger entre billes leur vitesse de translation normale au point de choc ; dans les mêmes conditions, un choc contre une bille immobile (condition : W'a = 0) fait rebondir la bille mobile selon la tangente au point de choc, même en présence de frottement.
3- Le cas du choc bille-bande est similaire à celui du choc entre billes, en mettant à zéro les trois quantités W'a, Ω'a et (M / M').
4- Dans le cas général où la compressibilité du tapis est suffisante pour pouvoir dissocier dans le temps les différents chocs élémentaires qui se produisent (chocs bille-bille, bille-bande et bille-tapis), les équations trouvées sont exactes.
5- Dans les quatre cas précédents, si le mouvement relatif entre les deux corps n'est pas suffisant pour vaincre le frottement (condition : u < 0), il y a alors adhérence pendant le choc et les équations doivent être modifiées en remplaçant la quantité fi (P*/M) / ||WCa|| par la quantité (2/7) / (1 + M/M'), ce qui donne (équations 1b) :
|
Wi = Wa + (P*/M) x* - (2/7) WCa / (1 + M / M') Ωi = Ωa + (5 / 7R) [ x* x WCa / (1 + M / M') ] W'i = W'a + (M /M') (Wa - Wi) Ω'i = Ω'a - (M / M') (R/R') (Ωa - Ωi) k = (1 + N) / (1 + M / M') |
Ces équations incluent également le cas parfait du "roulement corps N°1 sur corps N°2" juste avant le choc (condition : WCa = 0).
6- Si, juste avant le choc entre les deux corps, il y a immobilité du corps
N°2 (conditions : W'a = Ω'a = 0), avec une faible énergie
cinétique de rotation pour le corps N°1 (condition : Ωa
négligeable), un choc relativement frontal entre corps (condition :
Wa // x*) et un frottement faible (condition : fi négligeable),
alors les coefficients (e) et (N) sont reliés en première approximation par la
relation :
|
e = (1 - N2) / (1 + M / M') |
7- Le cas du choc horizontal queue-bille est très particulier : la queue choque à la fois la bille et la main posée sur le tapis. Le modèle du choc est alors différent : le vecteur percussion (P) est sensiblement parallèle à l'axe de la queue (condition : P // W'a et Ω'i = 0), avec une proportion d'énergie cinétique dissipée pendant le choc qui est sensiblement constante. Si (D) désigne l'excentricité de la queue par rapport au centre de la bille, la résolution vectorielle donne pour solution unique (équations 1c) :
|
Wi = W'a [1 + (1 - e - e K2 M'/M)1/2] / [K2 + M/M'] Ωi = (5/ 2R) (GC/R) x Wi W'i = W'a - (M/M') Wi K2 = 1 + (5/2) (D/R)2 |
8- Le cas du choc queue-bille avec un coup de queue incliné par rapport au plan du tapis, est similaire au cas du choc horizontal queue-bille. Si on suppose pour simplifier que la compressibilité du tapis est suffisante pour pouvoir dissocier dans le temps les deux chocs élémentaires qui se produisent (chocs queue-bille et bille-tapis), il suffit de remplacer dans les équations 1a les termes Wa et Ωa respectivement par les termes Wi et Ωi donnés dans les équations 1c.
Les équations générales qui régissent le mouvement d'une bille quelconque, juste après le choc qui a provoqué ce mouvement, sont données ci-après.
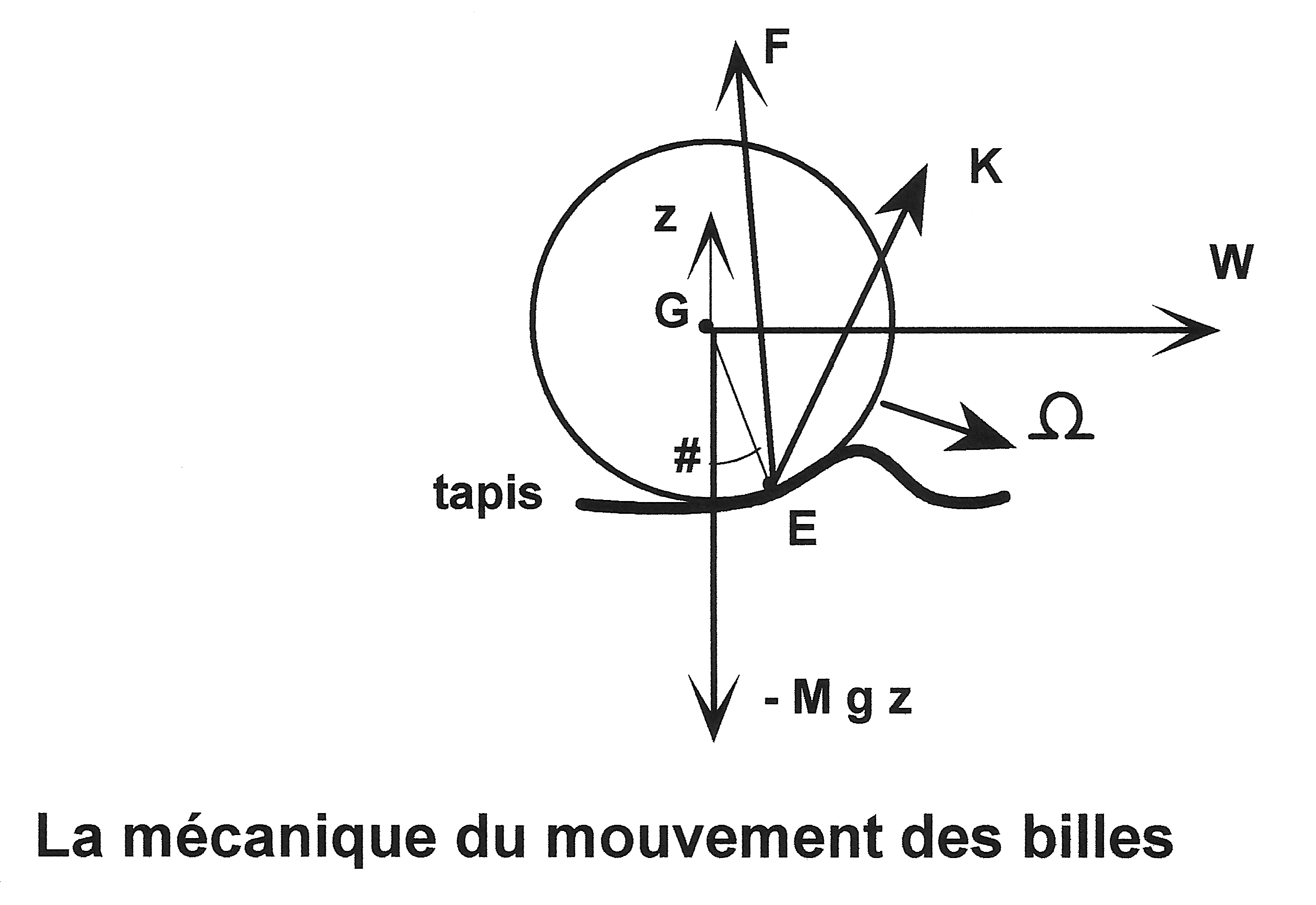
E, WE : point d'appui de la bille sur le tapis, et vecteur vitesse de glissement en E
F, K : force de réaction, et couple de frottement du tapis sur la bille
z : vecteur unitaire vertical, dirigé vers le haut
c : indice relatif à l'instant où la bille roule sans glisser sur le tapis
d v /dt : dérivée par rapport au temps du vecteur v
f, fc, fz : coefficient de frottement, coefficient de résistance à l'avancement, et paramètre de pivotement entre bille et tapis
g, t : accélération de la pesanteur, et temps
Les lois standards de la mécanique du mouvement d'une bille s'écrivent :
Principe fondamental de la dynamique :
M dW/dt = F - M g z
I dΩ/dt = GE x F + K
avec vecteurs W, Ω et F à déterminer.
Situations particulières :
1. Cas où la bille saute en l'air :
F = 0 et K = 0
2. Cas où la bille glisse sur le tapis (loi de Coulomb sur le frottement) :
E à la verticale de G (en négligeant la résistance à l'avancement par rapport au frottement)
F = M g ( z - f WE / ||WE||)
avec WE = W + z x (R Ω)
K horizontal négligeable par rapport à GE x F
K vertical = - (fz / R) (M g R) (Ω vertical) / ||Ω vertical||
3. Cas où la bille roule sans glisser sur le tapis :
W = - z x (R Ω)
K horizontal = 0
K vertical = - (fz / R) (M g R) (Ω vertical) / ||Ω vertical||
Il y a donc 3 équations pour 3 inconnues (W, Ω et F). La résolution vectorielle donne
pour solution unique (équations 2a) :
1. Cas où la bille saute en l'air :
|
W = Wi - g t z et Ω = Ωi |
2. Cas où la bille glisse sur le tapis (condition : t < tc) :
|
W = Wi - (t / tc) (Wi - Wc) Ω horizontal = Ωi horizontal + (5/ 2R) (t / tc) z x (Wi - Wc) Ω vertical = Ωi vertical [ 1 - (5/ 2R) (fz / R) (g / ||Ωi vertical||) t] tc = ||Wi - Wc|| / (f g) Wc = (5/7) [ Wi - (2 R/5) z x Ωi ] Ωc horizontal = (1/R) z x Wc = (5/7) [ (1/R) z x Wi + (2/5) Ωi horizontal ] F = M g (z - f WEi / ||WEi||) qui indique que la force F reste constante durant toute la phase de glissement |
3. Cas où la bille roule sans glisser sur le tapis (condition : t > tc) :
|
W = Wc [ 1 - fc (g / ||Wc||) (t - tc) ] Ω horizontal = (1/R) z x W Ω vertical = Ωi vertical [ 1 - (5/ 2R) (fz / R) (g / ||Ωi vertical||) t ] F = M g (z - fc Wc / ||Wc||) qui indique que la force F reste constante durant toute la phase de roulement |
Dans chaque cas, il suffit ensuite d'intégrer les équations en W et Ω pour obtenir la trajectoire et la rotation de la bille.
1- Dans le cas où la bille saute en l'air juste après le choc, la trajectoire est une courbe parabolique située dans un plan vertical.
2- Dans le cas où la bille reste en contact avec le tapis, elle commence par glisser dans un plan horizontal en décrivant une courbe parabolique, puis roule sans glisser selon une droite.
La synthèse complète de la théorie du billard, ainsi que la justification des affirmations données dans cet article, se trouvent dans l'ouvrage Billard - Théorie du jeu de Régis PETIT (voir la bibliographie).
Régis Petit est ingénieur en informatique à EDF.
Equations de base :
L'indice ' est relatif à au corps choqué (bille 2, bande ou tapis).
(C1) M Wi = M Wa + P
(C2) M' W'i = M' W'a + (-P)
(C3) I Ωi = I Ωa + GC x P
(C4) I' Ω'i = I' Ω'a + G'C x (-P)
avec : I = (2/5) M R2 et I' = (2/5) M' R'2
(C5) (Wi - W'i).x* = - N (Wa - W'a).x*
(C6) P = P* ( x* - fi WCa / ||WCa||)
(C6') WCa = (Wa - W'a) - [ (Wa - W'a).x* ] x* + x* x (R Ωa + R' Ω'a)
(C6") P* = k M (W'a - Wa).x*
Résolution :
Les relations (C1) et (C2) donnent W'i comme suit :
(C7) W'i = W'a + (M/M') (Wa - Wi)
Les relations (C3) et (C4) donnent Ω'i comme suit :
(C8) Ω'i = Ω'a - (M/M') (R/R') (Ωa - Ωi)
Les relations (C1), (C6) et (C6") donnent Wi comme suit :
(C10) Wi = Wa + (P*/M) (x* - fi WCa / ||WCa||)
Les relations (C3), (C6) et (C6") donnent Ωi comme suit :
(C11) Ωi = Ωa + (5/2)(1/R) x* x (Wa - Wi) = Ωa + (5/2)(1/R) fi (P*/M) x* x WCa / ||WCa||
Le remplacement de (C7) dans (C5) donne Wi comme suit :
(Wi - Wa).x* = ((1 + N)/(1 + M/M')) (W'a - Wa).x*
Le remplacement de (C10) dans cette dernière relation donne le coefficient k comme suit :
(C9) k = (1 + N)/(1 + M/M')
On démontre également que :
(C12) WCi = (Wi - W'i) - [ (Wi - W'i).x* ] x* + x* x (R Ωi + R' Ω'i) = u WCa
Le cas de l'adhérence pendant le choc est particulier. Elle survient lorsque le mouvement relatif entre les deux corps n'est pas suffisant pour vaincre le frottement, ce qui s'écrit :
(C13) WCi = 0
Le remplacement de (C13) dans (C12) donne la condition d'adhérence comme suit :
u < 0 qui inclut le cas WCa = 0
Les relations (C7)(C8)(C10)(C11) sont alors à modifier en remplaçant la quantité fi (P*/M) / ||WCa|| par la quantité (2/7) / (1 + M/M')
Equations de base :
L'indice ' est relatif à la queue.
(C21) M Wi = M Wa + P
(C22) M' W'i = M' W'a + (-P)
(C23) I Ωi = I Ωa + GC x P
avec : I = (2/5) M R2
(C24) Qa - Qi = e Qa
(C24') Q = (1/2) (M W2 + I Ω2 + M' W'2 + I' Ω'2)
Hypothèses :
- La bille est immobile juste avant le choc :
(C25) Wa = Ωa = 0
- La queue a un mouvement de translation juste avant le choc :
(C26) Ω'a = 0
- La queue choque la bille au point C : GC = - R x* et on pose : K2 = 1 + (5/2) (D/R)2
- La main ou le chevalet qui guide la queue absorbe totalement l'onde de choc transversale :
(C27) P parallèle à W'a
(C28) Ω'i = 0
- L'excentricité (D) de la queue n'est pas trop grande de façon que, juste après le choc, la queue et la bille se séparent automatiquement :
(C29) Wi.x* > W'i.x*
Résolution :
Les relations (C21) et (C25) donnent W'i comme suit :
W'i = W'a - (M/M') Wi
Les relations (C23), (C25) et (C2) donnent Ωi comme suit :
Ωi = (5/2)(1/R) (GC/R) x Wi
Les relations (C24')(C25)(C26) et (C28) donnent Qa et Qi comme suit :
Qa = (1/2) M' W'a2
Qi = (1/2) (M Wi2 + I Ωi2 + M' W'i2 )
Les relations (C23) et (C25) donnent Ωi2 comme suit :
Ωi2 = ((5/2)(D/R)(1/R))2 Wi2
Les relations (C24)(C27) et (C29) donnent Wi comme suit :
Wi = W'a [1 + (1 - e - e K2 M'/M)1/2] / [K2 + M/M']
La condition de séparation automatique entre queue et bille s'écrit alors :
(D/R)2 < (2/5)(1 + M/M')(1 - e (1 + M'/M))
Equations de base :
(M1) M dW/dt = F - M g z
(M2) I dΩ/dt = GE x F + K
avec : I = (2/5) M R2
(M3) F = M g [ z - (f WE / ||WE||) ]
(M4) WE = W + z x R Ω = W + z x R Ω horizontal
Hypothèses :
- La bille reste en contact avec le tapis au début et pendant la phase de glissement : Wi = Wi - (Wi.z) z et W.z = 0
- On néglige la force de résistance à l'avancement de la bille par rapport à la force de frottement : GE = - R z
- On néglige K horizontal par rapport au produit GE x F : K horizontal = 0
Résolution :
Les relations (M1) et (M3) donnent dW/dt comme suit :
(M1') dW/dt = - f g WE / ||WE||
Les relations (M2) et (M3) donnent dΩ horizontal /dt comme suit :
(M2") dΩ horizontal /dt = - (5/2) (1/R) z x (F / M) = - (5/2) (1/R) z x dW/dt
Les relations (M4) et (M2") donnent dWE/dt comme suit :
dWE/dt = dW/dt + z x R dΩ/dt = dW/dt + z x R dΩ horizontal /dt = dW/dt - (5/2) z x (z x dW/dt) = (7/2) dW/dt
Compte tenu de la relation (M1'), on en déduit que dWE/dt est parallèle à WE.
Donc WE garde une direction constante pendant le mouvement et WE peut s'écrire :
(M3') WE / ||WE|| = WEi / ||WEi||
Compte tenu de la relation (M3), F peut alors s'écrire :
(M3") F = M g [ z - (f WEi / ||WEi||) ]
F garde donc une amplitude et une direction constantes pendant le mouvement.
En intégrant la relation (M2"), Ω horizontal peut s'écrire :
(M2''') Ω horizontal - Ωi horizontal = - (5/2) (1/R) z x (W - Wi)
Compte tenu de la relation (M4), WE peut alors s'écrire :
(M4') WE - WEi = (W - Wi) + z x R (Ω horizontal - Ωi horizontal) = (W - Wi) - (5/2) z x (z x (W - Wi)) = (7/2) (W - Wi)
En fin de phase de glissement, on a W = Wc et WE = 0. Wc peut alors s'écrire :
(M8) Wc = Wi - (2/7) WEi = (5/7) (Wi - (2/5) R z x Ωi)
Compte tenu des relations (M3') et (M8), en intégrant la relation (M1'), W peut s'écrire :
W - Wi = - f g t (Wi - Wc) / ||Wi - Wc||
En fin de phase de glissement, on a W = Wc et t = tc. W et tc peuvent alors s'écrire :
(M10) W = Wi - (t/tc) (Wi - Wc)
(M10') tc = ||Wi - Wc|| / (f g)
Compte tenu des relations (M4') et (M8), WE peut s'écrire :
WE = (7/2) (1 - (t/tc)) (Wi - Wc) = (1 - (t/tc)) WEi
Equations de base :
(M1) M dW/dt = F - M g z
(M2) I dΩ/dt = GE x F + K
avec : I = (2/5) M R2
(M5) Le point E est décalé sur le devant de la bille selon un angle (#) : cos[#] = - (1/R) GE.z et on pose : fc = sin[#] / (2/5 + cos[#])
(M6) W = - z x R Ω
Hypothèses :
- La bille reste en contact avec le tapis pendant la phase de roulement : W.z = 0
- On néglige K horizontal par rapport au produit GE x F : K horizontal = 0
Résolution :
Les relations (M2) et (M6) donnent dW/dt comme suit :
dW/dt = - z x R dΩ/dt = - (R/I) z x (GE x F) = - (R/I) ( (F.z) GE - (GE.z) F )
La relation (M1) donne ensuite dW/dt comme suit :
dW/dt = - (R/I) ( M g GE - (GE.z) (M g z + M dW/dt) )
D'où :
(M11) dW/dt = - g (GE - (GE.z) z) / ((2/5) R - (GE.z)) = - g (R sin[#] W / ||W||) / ((2/5) R + R cos[#]) = - g fc W / ||W||
On en déduit que dW/dt est parallèle à W.
Donc W garde une direction constante pendant le mouvement et W peut s'écrire :
(M11') W / ||W|| = Wc / ||Wc||
Compte tenu de la relation (M1), F peut alors s'écrire :
(M11") F = M g [ z - (fc Wc / ||Wc||) ]
F garde donc une amplitude et une direction constantes pendant le mouvement. Le coefficient fc rend compte de la résistance à l'avancement de la bille sur le tapis.
En intégrant la relation (M11), W peut s'écrire :
(M12) Pour t > t arrêt_translation : W = 0
(M12') Pour t < t arrêt_translation : W = (1 - (t - tc)/(t arrêt_translation - tc)) Wc
(M12") t arrêt_translation = tc + ||Wc||/(fc g)
La relation (M6) donne ensuite Ω horizontal comme suit :
(1/R) z x W = - (1/R) z x (z x R Ω) = Ω - (Ω.z) z = Ω horizontal
Equations de base :
(M1) M dW/dt = F - M g z
(M2) I dΩ/dt = GE x F + K
avec :
I = (2/5) M R2
(M7) K vertical = - (fz / R) (M g R) Ω vertical / ||Ω vertical||
Résolution :
Les relations (M3") et (M11") donnent les relations suivantes :
En phase de glissement : (z x GE).(F/(M g)) = ( z x (-R) z ).(F/(M g)) = 0
En phase de roulement : (z x GE).(F/(M g)) = ( z x R (sin[#] (W/||W||) - cos[#] z) ).(F/(M g)) = R sin[#] ( z x (W/||W||) ).( z - fc (W/||W||) ) = 0
La relation (M2) s'écrit alors :
(M13) I dΩ vertical/dt = ((GE x F).z) z + K vertical = (z x GE).F + K vertical = K vertical = - (fz / R) (M g R) Ω vertical / ||Ω vertical||
On en déduit que dΩ vertical/dt est parallèle à Ω vertical.
Donc Ω vertical garde une direction constante pendant le mouvement et Ω vertical peut s'écrire :
(M13') Ω vertical / ||Ω vertical|| = Ωi vertical / ||Ωi vertical||
En intégrant la relation (M13), Ω vertical peut s'écrire :
(M14) Pour t > t arrêt_pivotement : Ω vertical = 0
(M14') Pour t < t arrêt_pivotement : Ω vertical = (1 - (t / t arrêt_pivotement)) Ωi vertical
(M14") t arrêt_pivotement = (2/5) R2 ||Ωi vertical||/(fz g)
Les différents vecteurs projetés dans le repère {x, y, z} de la queue peuvent s'écrire :
W = (0, V, 0)
Wi = (0, Vi, 0)
Wc = (0, Vc, 0)
Ω = (p, 0, r)
Ωi = (pi, 0, ri)
z = (0, 0, 1)
Les relations (M2''') (M8) (M10') et (M10) s'écrivent alors plus simplement :
:
p = pi - (5/2) (1/R) (Vi - V)
Vc = (5/7) (Vi - (2/5) R pi)
V = Vi - (t/tc) (Vi - Vc)
tc = |Vi - Vc| / (f g)
Si H est la hauteur d'attaque prise sur la bille, le choc queue-bille donne par ailleurs la relation suivante quel que soit l'effet de côté :
pi = (5/2) (1/R) Vi (1 - (H/R))
D'où :
p = (5/2) (1/R) (V - (H/R) Vi)
Vi - Vc = Vi (1 - (5/7)(H/R))
V = Vi - s f g t
s = Signe de [1 - (5/7)(H/R)]
En intégrant cette dernière relation, la distance y parcourue par la bille au temps t pendant la phase de glissement s'écrit alors :
y = Vi t - (1/2) s f g t2 = s (Vi2 - V2) / (2 f g)
Le glissement est pur pour p = 0, d'où : Vb = (H/R) Vi
Le glissement s'arrête pour p = - (1/R) Vc, d'où : Vc = (5/7) (H/R) Vi
Les distances parcourues par la bille (yb jusqu'à l'état de glissement pur et yc jusqu'à l'état de roulement) s'écrivent donc :
Pour H < R : yb = Vi2 (1 - (H/R)2) / (2 f g)
Pour tout H : yc = Vi2 |1 - ((5/7)(H/R))2| / (2 f g)
 Dernière mise à jour de la page : 3 février 2024.
Dernière mise à jour de la page : 3 février 2024.